基于MIDAS的钢桁梁检测静载轮位模型优化

朱莉鹏（沈阳铁路局工务检测所，沈阳110031）

基于MIDAS的钢桁梁检测静载轮位模型优化

朱莉鹏
（沈阳铁路局工务检测所，沈阳110031）

铁路钢桁梁桥静载试验中，利用Midas建立仿真模型，并提取杆件的最不利荷载轮位及其影响线，在这一过程中，发现最不利荷载轮位中所有试验编组的集中荷载均未通过桁梁节点的问题，通过分析其问题原因，优化Midas模型，解决了静载试验加载轮位错误的问题，提取出合理影响线，通过现场测试对比实测值与理论值，验证结果良好。

静载检测;MIDAS;铁路;钢桁梁;加载轮位;模型优化

【DOI】10.13616/j.cnki.gcjsysj.2016.12.124

1 引言

对于运营线路上的特大桥、大桥以及重要桥梁，规定每10年进行一次常规综合检定，静载测试作为其中的一项重要内容，为评估桥梁结构承载能力提供结论支撑，而试验列车加载位置的准确与否，直接影响测试结论的真实性与可信度。

2 模型概述

2.1 计算模型

以下承式钢桁梁为例，结构对称：左右两片桁架，纵梁、横梁、轨道均为对称布置；传力顺序：轴重→钢轨→枕木→纵梁→横梁→主桁节点→主桁杆件→端节点→支座。

对于铁路钢桁梁这种结构对称、荷载受力传递明确的桁架结构，在早期桥梁的设计过程中，采用平面理论进行设计；现行《铁路桥梁检定规范》（铁运函[2004]120号）[1]中各项检定指标亦采用平面理论，例如，桁梁杆件影响线、承载力检算的基本公式等。基于MIDAS建立平面模型具有单元节点少，荷载施加方便，工作量小等特点,目前，大多采用平面模型进行理论计算。

2.2 测试模型

按照杆件类型和受力特点，选取弦杆中跨下弦拉杆、跨中上弦压杆，腹杆中第一压杆（桥门架）、第一拉杆、吊杆、反复应力杆（交叉杆）等部位进行测试。参考控制杆件影响线及加载效率要求，选取铁路列车编组：1×DF8月+6×C80月满载车，列车首尾车轴间长度89.965m，长度能够覆全桥。该桥结构对称，荷载对称，故选取半跨进行测试。

3 MIDAS模型优化及静载轮位的确定

3.1 计算模型单元类型的选取

在结构力学原理中，认为钢桁梁杆件为二力杆，仅受轴力，节点为铰接，不传递弯矩。而实际上，节点板处经过铆钉群或螺栓群作用后，杆件间并非纯铰接或纯刚接,节点连接主要体现刚接特性，故利用MIDAS软件建立模型的过程中，钢桁梁杆件选取梁单元刚性连接。在基于MIDAS建立的平面模型中，施加移动荷载的前提是先设置车道，软件默认仅梁单元可设为车道单元，否则无法施加移动荷载，因此，下承式钢桁梁的车道设置在下弦杆（梁单元）上。

3.2 计算模型中最不利荷载轮位的提取过程

利用MIDAS软件确定静载试验列车加载轮位的步骤：（1）建立桥梁平面模型；（2）选取全桥下弦杆（梁单元）设置车道，施加自定义试验列车（现行最不利荷载试验工况）；（3）运行分析；（4）在分析结果中，通过移动荷载追踪器，分别提取重要典型杆件内力最不利时的荷载工况，即静载试验的加载位置。

3.3 计算模型中提取静载轮位时发现的问题

在结构力学原理[2]中，桁架结构属于节点受力，静载轮位中以试验列车的某一轮轴压在桁梁节点处为特征。按平面理论分析，桁梁杆件的影响线顶点必在节点上，只有当某一集中荷载作用在影响线顶点时，才有可能引起临界荷载，即最不利荷载位置，也就是我们要提取的静载轮位。而基于MIDAS建立的平面模型所提取的静载轮位出现了试验列车所有轮轴均未压在桁梁节点上的情况（见图1），并且其给出的影响线顶点不在节点位置，而在杆件中点，依据影响线初步判断，结论违背常识。

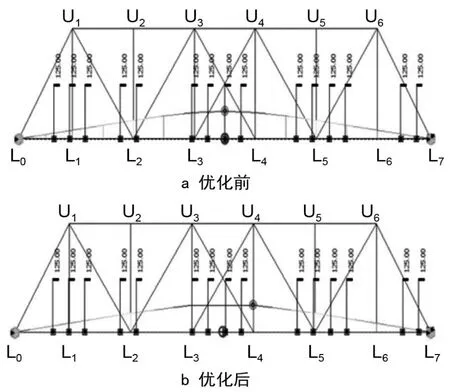
图1 优化前、后对比

3.4 计算模型问题原因分析

在MIDAS软件中，梁单元本身具有传递弯矩、轴力、剪力的特性，故而使理论上的二力杆件，在杆中表现出了弯矩的受力特性，最终所提取的最不利加载轮位，以试验列车某一轮轴压在杆件跨中为特征，而不是试验列车的某一轮轴压在桁梁节点为特征，造成了与结构力学原理相互矛盾的情况（见图1a）。

3.5 计算模型优化方法

基于上述问题，对仿真模型进行优化。将梁单元视为简支梁，在MIDAS移动荷载分析控制数据菜单中，梁单元加载位置按所有点加载，每个线单元上影响线点的数量默认为3，这3个点分别为梁单元端点和梁单元中点，分别对应轴力、剪力，以及弯矩。现将每个线单元上影响线点的数量调整为2，这2个点仅为梁单元的端点，这2个节点仅传递轴力和剪力，按节点法受力分解，经优化后杆件内部就仅传递轴力了（见图1b）。

3.6 计算模型优化前后对比

提取跨中下弦杆件L3、L4的加载轮位。桥梁计算长度为47.3456m（英制梁），自定义试验列车为1DF8月+3C80月，列车首尾全长53.965m，该桥为超静定结构。

1）经优化后其中一个集中荷载作用在L3节点上，即影响线的顶点上。影响线顶点竖标相差4.82%。

2）经优化后跨中下弦杆件L3、L4的影响线的形状、面积均发生了改变。影响线形状由三角形变为等腰梯形，影响线面积相差1.17%。

3.7 优化模型理论计算值与实测值对比

对比各杆件计算值与实测值：除第二压杆U4L3实测值略大于计算值，经推算至“中-活载”为62.63MPa,远小于钢材材料容许应力170 MPa，其余实测值均小于计算值，结构静强度满足要求。各节点挠度实测值小于计算值，结构竖向刚度满足要求。通过对比分析，可见主桁结构强度、刚度有一定的储备，同时也反映出结构本身高跨比较大，属超静定结构等特点。

表1 主轮位下各杆件实测值与理论计算值 MPa

4 结语

MIDAS模型经优化后，主测杆件静载轮位及其影响线更加合理，更符合平面理论下的桁架结构。由于计算模型优化前后其模型本质是不同的，前者按梁考虑杆件传递弯矩，后者按杆考虑仅传递轴力，虽然计算结果相差不大，但容易掩盖错误的本质，正所谓“失之毫厘谬以千里”。经现场实际测试，对比分析实测值与计算值，验证结构静强度、竖向刚度安全可靠。

【1】铁运函[2004]120号铁路桥梁检定规范[S].

Steel Truss Girder Detection Based on MIDAS Static Load Wheel Model Optimization

ZHU Li-peng
(Shenyang Railway Bureau Work Section Testing Division,Liaoning Province,Shenyang110031,China)

In the rail way steel truss static load test, the simulation model which is based on MIDAS, it can extract the unfavorable load wheel andinfluence line of the bar. In this process,we found that all concentrated loads organized in testing have not pass the truss nodes in unfavorable loadwheel. This paper via analysing the reason, optimizing the MIDAS model, solves the static load test wheel loading problem, giving a reasonableaffecting line.Compared the test value with theoretical value by field test ,a satisfying result is verified.

static load test;MIDAS; railway; steel truss beam; loaded wheel;model optimization

U446.1

A

1007-9467（2016）12-0060-02

2016-10-17

朱莉鹏（1979～），男，辽宁沈阳人，工程师，从事桥梁检测数据分析研究。