积分方法的探索与补充——辅助积分法*

吴邦昆

(合肥职业技术学院，安徽巢湖238000)

积分方法的探索与补充
——辅助积分法*

吴邦昆

(合肥职业技术学院，安徽巢湖238000)

有些三角函数有理式的积分，用传统的万能代换法化为代数有理式积分仍然比较复杂，求积分过程相当困难，有时甚至无法积出.而用辅助积分法解决这类三角函数有理式的积分有时过程简洁，思路清晰明了，为我们求三角函数有理式的积分提供了一种新方法和新思路，是对传统积分方法的有益补充.

积分方法;补充;辅助积分法

解决一些用常规的万能代换法不易求出的三角函数有理式积分，用辅助积分法积分有时过程简洁，思路清晰明了.辅助积分法就是选择与原积分结构相似的辅助积分，利用辅助积分求出原积分的积分方法，这种方法无疑是对传统积分方法的有益补充和探索.

1 辅助积分法的使用原则及步骤

运用辅助积分法的关键是要选择好辅助积分，寻求辅助积分应注意4条原则.①辅助积分与原积分在结构上相似;②辅助积分之间或辅助积分与原积分之间能通过恰当组合化成一个易求积分;③原积分与辅助积分之间关系要明确;④对于三角函数有理式的积分，它的辅助积分应该仍为一个三角函数有理式积分.

运用辅助积分法求三角函数有理式积分的步骤是:首先应根据原积分的三角函数有理式特点选择好辅助积分(一个或多个);再利用辅助积分之间的不同组合(有几个辅助积分就要形成几个不同组合)构成不同的方程;最后解这个关于辅助积分的方程组，求出辅助积分，从而求出原积分.

2 辅助积分法的应用

显然要求出此有理式积分比较繁琐，而用辅助积分法，求解过程就简单得多.

于是有

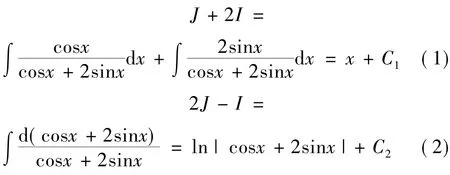
由式(1)及式(2)解得

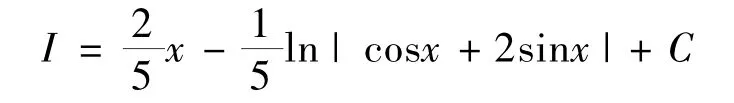
分析:此题若用万能代换方法将其化成代数有理式求积分，其过程一定繁琐，甚至求不出来，但用辅助积分法就可以得到比较清晰明了的解答.

解 令I1=(辅助积分)，I2=(辅 助 积 分 )，I3=d x(辅助积分)，则I=3I1+I2+4I3.

于是有

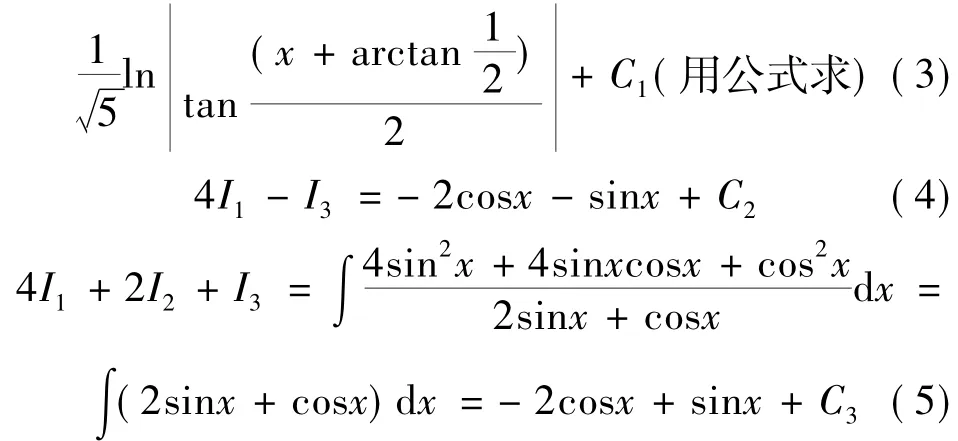
从而(3)+(4)得

代入式(3)得

将I1、I3代入式(5)得

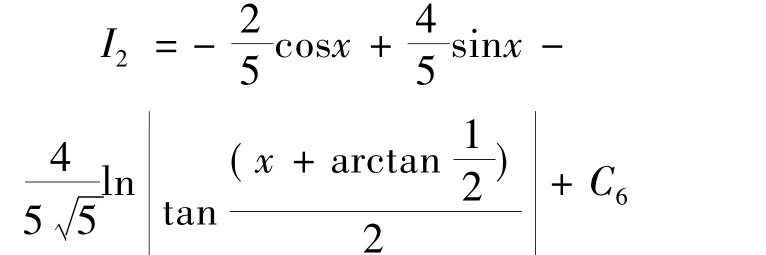
所以，I = 3I1+ I2+ 4I3= sin x +

解 令I1=(辅助积分)，I23d x(辅助积分)，则I=2I1－I2.

从而有

由式(6)、(7)解得

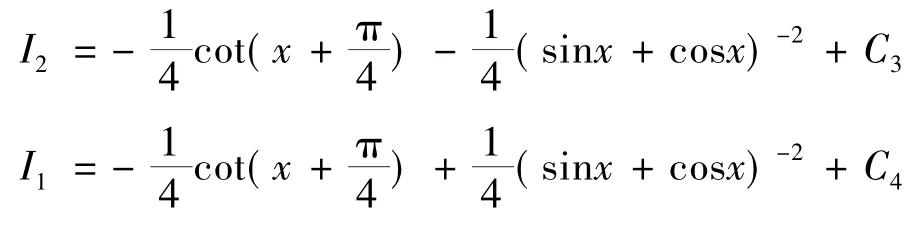
解 令I1=(辅助积分)，I2=(辅助积分)，则I=2I1.于是有

由式(8)、式(9)解得

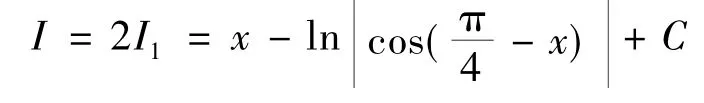
解 令I1=(辅助积分)，I2=(辅助积分)，则I=3I1+4I2.于是有

O231.2

:A

:1008－7974(2016)06－0044－03

10.13877/j.cnki.cn22－1284.2016.12.014

2016－07－20

安徽省高校省级质量工程项目“《高等数学》精品资源共享课程”(2013gxk161);合肥职业技术学院质量工程项目“《高等数学》精品课程”(JPKC201302);安徽省高校人文社科重点项目“大数据背景下高职学生学习力研究”(SK2015A734)

吴邦昆，安徽庐江县人，副教授.