工件加工时间非增的并行分批排序问题的最优在线算法❋
农庆琴, 苗利辉
(中国海洋大学数学科学学院,山东 青岛 266100)
工件加工时间非增的并行分批排序问题的最优在线算法❋
农庆琴, 苗利辉
(中国海洋大学数学科学学院,山东 青岛 266100)
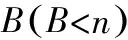
排序;并行批;在线;算法;竞争比
并行分批排序模型中的机器是批处理机,每次可同时加工至多B(B≥2,称为机器的批容量)个工件。根据批容量的特征,并行分批排序可分为2种类型:批容量无界(记为B=∞);批容量有界(记为B Cmax=max1≤j≤nCj 最小,其中Cj为工件Jj的完工时间。采用R.L.Graham等[1]提出的三参数法,该问题可记为 1|on-line,rj,pjnon-increasing,B 衡量一个在线排序算法A的性能最常用的指标是它的竞争比RA。对于最小化目标函数的在线排序问题,竞争比RA定义为对问题的所有实例运行该在线排序算法所得目标函数值与相应离线排序的最优值比值的上确界,即 关于并行分批排序问题的研究是近十多年来排序论的研究热点。学者们最先着手的是单机、批容量无界的排序模型的研究。对于排序问题1|on-line,rj,B=∞|Cmax,DengXT等[2],ZhangGC等[3]分别独立地设计出了竞争比是1+α的在线算法,并证明该排序问题不存在竞争比小于1+α的在线算法,从而证明相应算法的最优性,其中α满足等式α2+α=1。PoonCK等[4-5]给出了一族竞争比均为1+α的在线算法。上述算法都利用了等待的思想,不等待的在线算法竞争比不可能小于2[6]。对于此问题的一些特殊情况,RichardandPR等[7],YuanJJ等[8]给出了等待时间更少的在线算法。 P|on-line,rj,pj=1,B 给出了竞争比为1+α的在线算法,并证明该算法是最优的。 本文研究批容量有界、工件的加工时间非增的并行分批在线排序问题 1|on-line,rj,pjnon-increasing,B 给它设计一个竞争比是1+α的在线算法,并证明该算法是最优的。 探讨批容量有界、工件的加工时间非增的并行分批在线排序问题 1|on-line,rj,pjnon-increasing,B 的在线算法。不妨设r1≤r2≤…≤rn,由于工件的加工时间非增,有不等式p1≥p2≥…≥pn成立。记U(t)为t时刻已到达但尚未开工的工件集合,|U(t)|为U(t)中工件的数目,算法如下: 算法EF(EarlyFirst): 若|U(t)|=0:等待,更新U(t)。 若0<|U(t)| 若|U(t)|≥B:如果有机器空闲,则将U(t)中B个编号最小的(即最早到达的)工件组成一批开始加工,更新U(t)。 该算法的主要思想是:在机器空闲时需要决定是否加工待加工的工件,当待加工的工件数超过批的容量B时,优先选取早到的工件进行加工(由于工件的加工时间非增,这里实际上意味着长工件被优先选取);当待加工的工件数不足B个时,根据当前的时刻是否大于αp1再决定是否开工——若当前时刻小于αp1不加工,继续等待新工件;若当前时刻大于或等于αp1,不再等待,立刻将当前待加工的工件作为一批开始加工。αp1是一个关键时刻,在此时刻之前,只有待加工的工件达到B个才考虑开始加工,在此时刻之后,一旦有工件待加工、机器空闲,就立刻开始加工。 排序问题1|on-line,rj,B 定理1.1 对于1|on-line,rj,B 显然,每个工件加工时间均为1的实例是排序问题1|on-line,rj,pjnon-increasing,B 推论1.1 对于排序问题 1|on-line,rj,pjnon-increasing,B 不存在竞争比小于1+α的在线算法。 为了分析算法EF的竞争比,下面介绍一种分批规则。 FBLPT(FullBatchLongestProcessingTime)规则: 步骤一 将所有工件按加工时间的非增顺序排列,形成一个队列L。 步骤二 若队列L的工件数不少于B个,将排在最前的B个置于一批中,并将这B个工件从队列L中删除;否则将L中余下的所有工件置于一批中。 定理1.2 算法EF是在线排序问题 1|on-line,rj,pjnon-increasing,B 的竞争比为1+α的在线算法。 证明 给定任一实例I,算法EF输出的排序记为σ。设σ中总共有l批,分别记为B1,B2,…,Bl,并设 s(B1) 其中s(Bi)(1≤i≤l)为批Bi的开工时间。算法EF优先加工早到达的工件,而早到达的工件加工时间较长,因此必有Bi(1≤i≤l-1)中的工件加工时间均不小于它之后的批中工件的加工时间,于是 p(B1)≥p(B2)≥…≥p(Bl) 成立,其中p(Bi)(1≤i≤l)为批Bi的加工时间。显然,最长工件J1必在B1中。 设排序σ中[t1,t2]是时间区间[0,Cmax]内满足如下特征之一的最后时间段:(1)机器在[t1,t2]空闲;(2)机器在[t1,t2]内加工某一非Bl的不满批。 设排序σ中t2之后开工的批分别为 Bk,Bk+1,…,Bl, 情形一 在[t1,t2]时间段内机器空闲。 若t2>αp1,因为算法EF在αp1时刻之后的排序规则是一旦有工件待加工、机器空闲,就立刻开始加工工件,[t1,t2]时间段内机器空闲说明t2之后开工的工件(即Bk,Bk+1,…,Bl中的工件)到达时间均不早于t2,综合引理1.1得 若t2≤αp1,则Bk必为σ的首批,J1在该批中(否则Bk的开工时间t2至少为p1),于是P≥p1,下述不等式成立: 情形二 在时间段[t1,t2]内机器在加工某一非Bl的不满批。 则该批为Bk-1,t1和t2分别为它的开工、完工时间。由于Bk-1是不满批,根据算法EF的规则可知, t1≥αp1, (1) (2) 下面讨论2种子情形。 (I)k=2,即Bk-1为σ的首批B1。 (II)k≥3,即σ中Bk-1之前至少有一批加工。 由推论1.1和定理1.2可得以下结论。 推论1.2 算法EF是在线排序问题 1|on-line,rj,pjnon-increasing,B 的最优在线算法。 本文首先证明在线排序问题 1|on-line,rj,pjnon-increasing,B 不存在竞争比小于1+α的在线算法,然后设计算法EF,证明该算法是相应在线排序问题的最优在线算法。 [1]GrahamRL,LawlerEL,LenstraJK,R,etal.Optimizationandapproximationindeterministicsequencingandscheduling[J].AsurveyAnnalsofDiscreteMathematics, 1979, 5(2): 287-326. [2]DengXT,PoonCK,ZangYZ.Approximationalgorithmsinbatchprocessing[J].JournalofCombinatorialOptimization, 2003, 7: 247-257. [3]ZhangGC,CaiXQ,WongCK.On-linealgorithmsforminimizingmakespanonbatchprocessingmachines[J].NavalResearchLogistics, 2001, 48: 241-258. [4]PoonCK,YuWC.Aflexibleon-lineschedulingalgorithmforbatchmachinewithinfinitecapacity[C].Hongkong: 5thConferenceonOptimization:TechniquesandApplication(ICOTA'01), 2001. [5]PoonCK,YuWC.Aflexibleon-lineschedulingalgorithmforbatchmachinewithinfinitecapacity[J].AnnalsofOperationsResearch, 2005, 133: 175-181. [6]LiuZH,YuWC.Schedulingonebatchprocessorsubjecttojobreleasedates[J].DiscreteAppliedMaths, 2000, 105: 129-136. [7]RichardandPQ,RidouardF.On-lineschedulingonasinglebatchingmachinetominimizethemakespan[C].Portugal: 6thInternationalConferenceonIndustrialEngineeringandProductionManagement(IEPM'03), 2003. [8] 原晋江, 农庆琴. 平行批排序最小化最大完工时间在线算法的一个注记[J]. 郑州大学学报(理学版), 2006, 38(3): 1-3. Yuan J J, Nong Q Q. A short note on on-line algorithms for single batch machine to minimize makespan [J]. Journal of Zhengzhou University(Natural Science Edition), 2006, 38(3): 1-3. [9] Poon C K, Yu W C. On-line scheduling algorithm for a batch machine with finite capacity [J]. Journal of Combinatorial Optimization, 2005, 9(2): 167-186. [10] Liu P H, Lu X W, Fang Y. A best possible deterministic on-line algorithm for minimizing makespan on parallel batch machines[J]. Journal of Scheduling , 2012, 15: 77-81. [11] Tian J, Cheng T C E, Ng C T, Yuan J J. Online scheduling on unbounded parallel-batch machines to minimize the makespan [J]. Information Processing Letters, 2009, 109: 1211-1215. [12] Zhang G C, Cai X Q, Wong C K. Optimal on-line algorithms for scheduling on parallel batch processing machines [J]. IIe Transactions, 2003, 35: 175-181. [13] Lee C Y, Uzsoy R, Martin Vega L A. Efficient algorithms for scheduling semiconductor burn-in operations [J], Operations Research, 1992, 40: 764-775. AMS Subject Classification: 90B35 责任编辑 陈呈超 An Optimal On-Line Algorithm for a Parallel-Batching Scheduling with Non-Increasing Processing Time Jobs NONG Qing-Qin, MIAO Li-Hui (School of Mathematical Science, Ocean University of China, Qingdao 266100, China) In this paper a parallel-batching scheduling to minimize the maximum completion time is considered. There arenjobs to be scheduled on a parallel-batching machine. The machine can handle up toBjobs as a batch simultaneously, and all the jobs in a batch start and complete at the same time. Once a batch is started, it cannot be stopped until its completion. Each jobJjhas a processing timepjand a release daterj. Each pair of two jobsJiandJjsatisfies thatpi≥pjifri≤rj. Each job becomes available at its release date. The information of a job, including its release date and its processing time, is unknown until its arrival. The problem involves assigning all the jobs to batches and determining the sequence of batches so as to minimize the makespan (the maximum completion of the jobs). In this paper an optimal on-line algorithms for the problem is designed. scheduling; parallel-batching; on-line; algorithm; competitive ratio 国家自然科学基金项目(11201439;11271341);教育部博士点专项基金新教师基金项目(20120132120001);山东省自然科学基金项目(ZR2012AQ12)资助SupportedbytheNationalNaturalScienceFoundationofChinaundergrantnumber11201439and11271341.ThisworkwasalsosupportedinpartbytheDoctoralFundofMinistryofEducationofChina(20120132120001)andbytheShandongProvincialNaturalScienceFoundationundergrandnumberZR2012AQ12 2014-11-25; 2015-10-15 农庆琴(1978-),副教授,博士,研究方向:组合最优化。E-mail:qqnong@ouc.edu.cn O A 10.16441/j.cnki.hdxb.20140295 农庆琴, 苗利辉. 工件加工时间非增的并行分批排序问题的最优在线算法[J]. 中国海洋大学学报(自然科学版), 2017, 47(1): 126-130. NONGQing-Qin,MIAOLi-Hui.AnOptimalon-linealgorithmforaparallel-batchingschedulingwithnon-increasingprocessingtimeJobs[J].PeriodicalofOceanUniversityofChina, 2017, 47(1): 126-130.

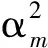
1 本文主要结果
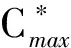
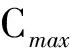
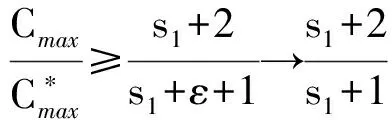

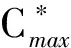
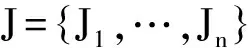
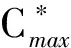
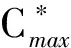
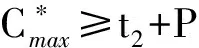

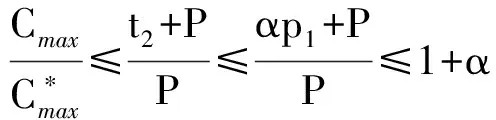
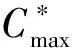
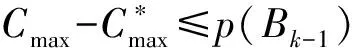
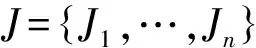
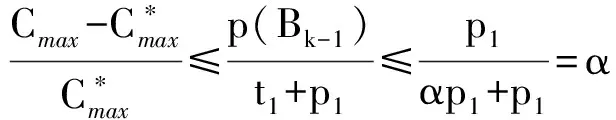
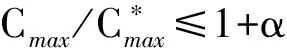
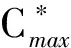
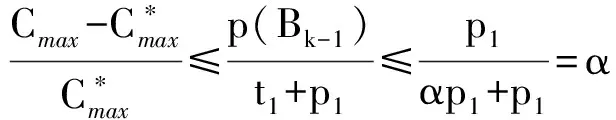
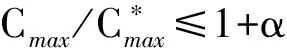
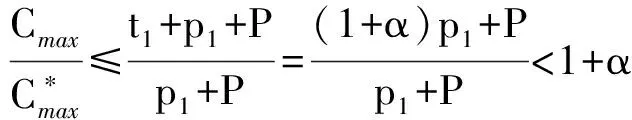
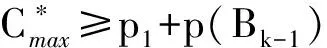
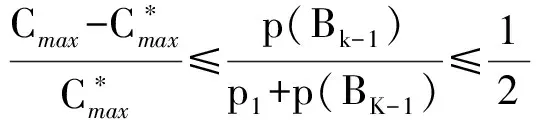
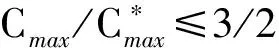
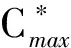
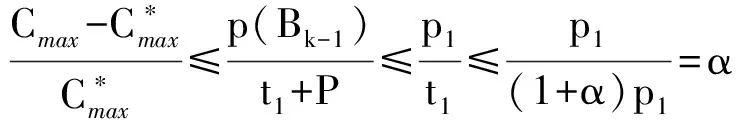
2 结论

