基于ANFIS改进的大气腐蚀环境缺失数据填补方法
(北京科技大学 a.自动化学院;b.新材料技术研究院,北京 100083)
基于ANFIS改进的大气腐蚀环境缺失数据填补方法
石雅楠a,付冬梅a,支元杰a,陈闽东b
(北京科技大学 a.自动化学院;b.新材料技术研究院,北京 100083)
目的针对大气腐蚀中重要环境数据缺失的复杂问题,提出一种相关因素(Relevance Factors)和自适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System)结合的方法(RF-ANFIS)对缺失数据进行填补。方法首先采用相关因素方法计算缺失数据和多项环境因素间的相关程度,筛选出相关系数较大的因子,然后应用ANFIS构建缺失数据与所选环境因子的关系模型。最后以二氧化硫数据为具体对象,采用北京2015年的气象数据对所建立的模型进行检验。结果经过改进的RF-ANFIS模型在最优情况下样本均方误差为0.696,在14个测试样本中有13个相对误差在20%以内,针对有限样本的数据分析中更为适用。结论该方法有效提高了大气腐蚀环境数据缺失的填补精度,对在数据缺失情况下预测大气腐蚀速率具有重要意义。
大气腐蚀;缺失数据;相关因素;ANFIS
大气腐蚀中缺失数据的填补是建模与应用中重要且具有一定难度的研究课题。根据 ISO 9223—2012标准,金属大气的腐蚀速率与环境中的二氧化硫浓度、氯化物浓度、温度以及湿度四个因子息息相关,但这些腐蚀因子由于人为疏忽、信息获取的滞后性等客观因素常有缺失,因此探索合适的精确度高的填补方法是实际工程亟待解决的难题。
目前腐蚀数据的处理方法主要集中在灰色模型[1—4]和 BP网络[5—7]。灰色系统中较常用的GM(1,1)模型仅适用于单变量对输出变量的预测,如利用一维时间序列建模,这种方法可获取信息少,无法考虑多维环境因素对腐蚀因子的影响。BP网络虽然可用于多维数据,但其需要大量的样本和长时间的训练才能得到较为准确的结果,且容易产生局部最优和过拟合,在腐蚀数据样本量有限时预测效果往往不理想。近年来专家将模糊神经网络逐渐应用于腐蚀数据的分析[8—11],模糊神经网络有效融合了模糊推理系统和神经网络的优点,在一定程度上克服了由于原始数据样本量过小而影响预测效果的问题。当数据样本维度较高时,模糊神经网络结构的特殊性会导致维数灾难而无法计算,所以如何有效实现降维就成了解决问题的一个途径。
基于上述原因,文中以二氧化硫缺失数据的填补为例,不同于传统利用多维环境因素或在一维时间序列上预测大气数据的单一模式,而将二者充分结合以挖掘更多信息,并通过相关因素(Relevance Factors)对所构建的ANFIS(Adaptive Neuro-Fuzzy Inference System)进行简化,进而建立二氧化硫的缺失预测填补模型。该研究对工程应用中填补二氧化硫一类有限样本的腐蚀数据具有实际意义。
1 数据收集与预处理
文中的数据来源于腐蚀站点提供的北京 2015年3月19日至2015年6月5日的环境数据和腐蚀数据。环境数据含有气温、风力、湿度、天气状况、降水量、PM2.5、PM10、O3、NO2共9个因素,腐蚀数据即二氧化硫浓度。文中选用了统一的 Excel表格进行规范化,MATLAB可以方便地将数据导入和导出表格。气象数据的采集是按小时进行的,每小时采一次,一天应有24组数据,表1仅列出了北京市某一天的10条数据。

表1 部分原始环境数据和腐蚀数据Table 1 Part of the original environmental data and corrosion data
ISO 9223—2012标准中统计二氧化硫浓度的最小单位为日,所以数据预处理的目的是将原始小时化的数据转换成以日为单位的样本,填补目标也为二氧化硫的日平均浓度。首先将所有数据量化,根据风力等级表将风力转换成区分度更高的风速。研究表明[12],日照时间是影响腐蚀的重要因素之一,而日照时间可通过每小时的天气状况(晴、阴、多云、雨雪等)推断得到,对天气状况处理时将晴记为1,其他情况记为0。然后将数据进行转换,每日的日照时间和降水量由相应每小时的数据累加得到,而其他所有因素则求日平均值作为对应数据。最后经过数据预处理后共得到79个样本用于研究。
2 RF-ANFIS模型
模糊神经网络的结构具有多样性的特点,比较常用的是Jang提出的ANFIS系统。实际应用中,网络生成的模糊规则数为各输入变量的隶属度函数个数之积(例如网络有m个输入变量,每个变量隶属度函数个数为n,模糊规则数即为nm)。因此在隶属度函数个数(一般取3~5)变化不大的情况下,网络的输入变量不宜过多,否则生成的规则数过大不易于实现[13]。针对ANFIS这一应用中的问题,文中引入相关因素的分析降低网络的复杂性,进而提出了一种RF-ANFIS预测模型,结构如图1所示。
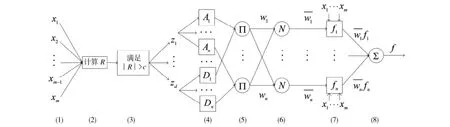
图1 RF-ANFIS预测模型结构Fig.1 Structure of RF-ANFIS prediction model
第一层为所有变量的输入层,假定输入变量为m维,则输出函数为:

第二层为相关因素计算层,计算每个输入变量xk与输出变量y之间的相关系数。相关因素分析是研究随机变量之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度的一种统计方法。相关系数R表示相关方向和相关程度。R在(0,1)之间为正相关,在(-1,0)之间为负相关,等于1为完全正相关,-1为完全负相关,0为不相关。变量kx与变量y之间的相关性系数公式为:本值和样本均值。
第三层为相关因素判断层,通过相关性系数的大小对输入变量进行取舍。设定一个常量c,判断规则为若|R|大于c则将对应的输入变量输出至下一层,否则留在这一层。由此已将m维的原始数据降至d维(d<m)。
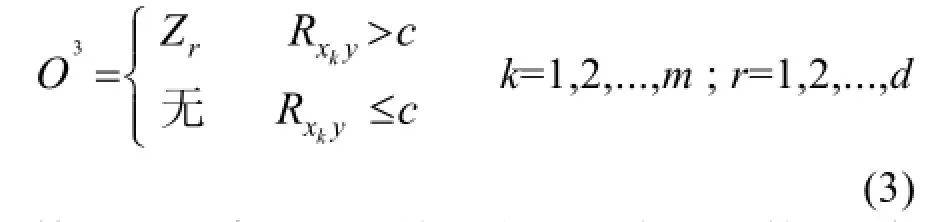
第四层为降维后的输入变量的隶属函数层,负责输入信号的模糊化。对于一阶Takagi-Sugeno模糊系统具有如下模糊规则:
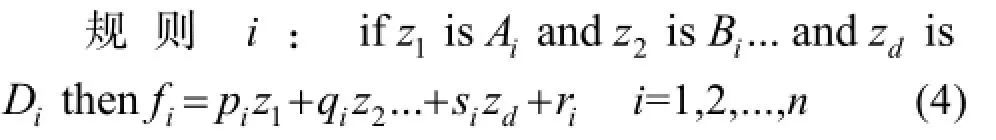
该层的输出函数为:
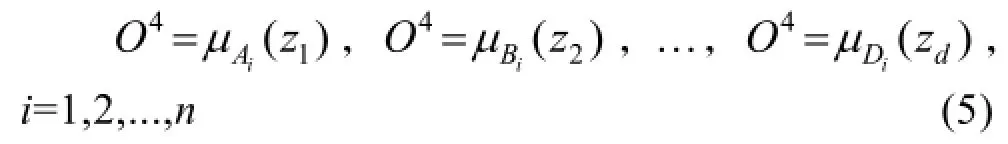
式中:1z到dz是经过相关系数判断后选出的输入变量,4O是iA到iD的隶属函数值,表示1z到

式中:xkl和xk表示输入变量xk的第l个样本值和样本均值;yl和y表示输出变量y的第l个样zd分别属于 Ai到 Di的程度,n是隶属度函数的个数。μAi(x)到 μDi(x)可以是任意合适的参数化隶属函数,如一般的钟型函数,以 μAi(x)为例:
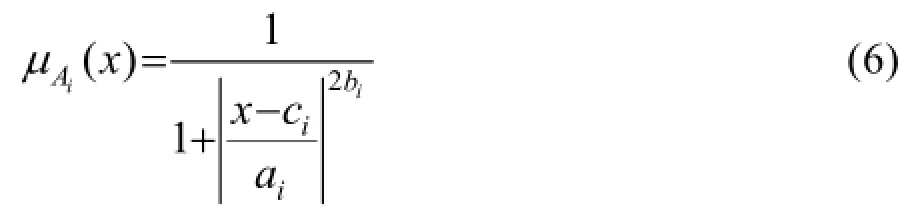
第五层为规则的强度释放层,负责将输入信号相乘,每个节点的输出代表该规则的可信度。输出函数为:

第六层为所有规则强度的归一化,第i个节点计算第i条规则的归一化可信度。输出函数为:

第七层为计算模糊规则的输出,这一层的每个节点i为自适应节点。输出函数为:

式中:wi为第六层的输出,为该节点的参数集,称为后件参数。
第八层为一个固定节点,计算所有输入信号的总输出,输出函数为:

在第五层至第八层中,通常采用一种反向传播算法和最小二乘法的混合学习算法分别对ANFIS的前件参数和后件参数进行训练。首先输入信号沿网络正向传播至第七层,在前件参数不变的情况下采用最小二乘法调节后件参数,然后信号继续沿网络正向传播直到第八层,将获得的误差信号沿网络反向传播,进而调节前件参数。这种方法不仅可以降低梯度法中搜索空间的维数,而且大大提高了收敛速度[14]。
3 仿真过程及结果
以北京市二氧化硫为例进行仿真,仿真过程可平移至其他环境参数缺失数据的补偿中。将79个样本随机分为65个训练样本和14个测试样本,根据第2节中RF-ANFIS模型的结构逐层分析,通过改变参数c的值改变筛选的输入变量d的个数,并与传统仅利用多维环境因素和仅在一维时间序列上预测的方法作对比。
3.1 建模步骤
1)相关因素分析。在收集到的样本中二氧化硫是一个时序数据,传统工程上采用滚动预测的方法建立二氧化硫缺失预测模型,但该方法仅利用了二氧化硫自身的信息而未考虑其他因素对样本的影响。文中挖掘二氧化硫与各环境参数间的相关性,并考虑二氧化硫自身的时序特征,第t天的二氧化硫浓度与当日的环境数据以及前五日的二氧化硫浓度的相关性系数见表2,其中Ct-1为第t-1天的二氧化硫,Ct-2表示第t-2天的数据,以此类推。

表2 二氧化硫浓度与各因子的相关性系数Table 2 Relevance coefficient of the concentration of SO2and other factors
经过相关性分析发现,其中二氧化硫与PM2.5,PM10,NO2,Ct-1,Ct-2五个因子关联性较明显。二氧化硫与前三者相关是因为雾霾天气时二氧化硫在空气中会转化成硫酸盐,导致硫酸盐颗粒达到40 μg/m3以上,致使PM2.5,PM10,NO2超标[15]。第t天的二氧化硫与t-1天和t-2天的相关性大也证明了其本身的自相关性。由此相关因素分析方法有效将十四维(m=14)的复杂问题转化成五维(d=5)的可计算网络,同时排除了干扰因素的影响,为ANFIS的建模打下基础。
2)ANFIS建模。根据ANFIS的结构,网络固定为五层。首先设定c=0.2,此时选择出的输入变量个数d=5(Ct-1,PM2.5,PM10,NO2,Ct-2),输出变量个数为1,每个输入变量的隶属度函数个数n=3。输入的模糊隶属度函数选择钟型函数,输出层选择一阶线性模糊推理系统即一阶Sugeno模糊模型,采用网格分割法生成FIS。网络学习算法选择混合学习算法。目标误差为 0.001,训练次数设定为200次。利用训练样本训练网络,在训练过程中,为提高函数逼近的效果,可对其隶属度函数类型、函数个数n、训练次数等指标进行适当的调整。利用训练网络学习的结果对测试样本进行检测,将预测结果与真实数据相比较,获得样本分布图,分析误差。
继续改变c的值,令c=0.4,此时选出的输入变量个数为d=4(Ct-1,PM2.5,PM10,NO2),输出变量个数仍为1,重复上述调参数的过程;再令c=0.45和c=0.5,此时选出的输入变量个数分别为d=3(Ct-1,PM2.5,PM10)和d=2(Ct-1,PM2.5),调整参数比较不同输入变量下的网络性能。
3.2 仿真结果
经过上述建模过程后,将c取不同值时RF-ANFIS模型的预测结果与文献[7]中BP网络时间序列和文献[6]中 BP网络多维因素建模的方法进行比较。表 3是五种建模方法在误差和计算时间上的比较,可以看出,首先对于样本的准确率,RF-ANFIS模型在c=0.4时不论是整体的均方误差还是单个样本的相对误差都是几种情况中最优的,c=0.45其次。当c=0.5,输入变量减少为2个时,网络性能已开始降低,这说明仅用Ct-1,PM2.5两个输入变量做预测有偏差,PM10对于二氧化硫的预测同样重要,而c=0.2时效果也不理想。这充分说明了ANFIS的输入变量并不是越多越好,相关系数为0.222的Ct-2加入到网络中反而对二氧化硫的预测形成了干扰。对于计算时间,BP网络时序建模由于其网络构造的简单性用时最短,RF-ANFIS随着c的减小,输入变量依次增多,使得网络生成的规则呈幂指数变化用时也就越长。因此综合上述因素,如果不考虑计算时间,只追求样本的精确度,优先选择c=0.4时的RF-ANFIS模型;如果在样本精确度达到一定程度时,希望节省计算时间,优先选择c=0.45的RF-ANFIS模型。

表3 各方法参数对比Table 3 Comparison of different methods
表 4列举了部分训练样本真实值和四种方法方法预测值的比较,从单个样本的预测中可以看出,c=0.4时预测值与真实值几乎完全相同,c=0.45时误差在1%以内,同样与真实值近似。BP网络的平均误差均大于10%,且个别样本出现极大误差,这也体现了BP网络在样本量不足的情况下准确性降低。

表4 部分训练样本不同方法预测值和相对误差对比Table 4 Comparison of predicted values and relative errors of different methods in part of training samples
c=0.4时的RF-ANFIS模型与BP网络时间序列和多维因素建模在测试样本上的对比如图 2所示。这14个训练样本中有9个预测结果优于多维因素建模,13个优于时间序列建模。由此可得,经过相关因素分析后,降低了传统ANFIS维数灾难的影响,有效地将难题转化为低维的可解决问题,说明应用RF-ANFIS模型对缺失数据的处理是可行的。同时该方法可以通过改变常量c的值控制所选择的输入变量d的个数,在经过多次仿真后寻找最佳的网络结构,结果比较理想。

图2 三种建模方法测试样本预测值与真实值比较Fig.2 Comparison of predicted values and real values of three methods in test sample
4 结语
1)相关因素的引入为ANFIS在多维数据样本适用局限性的问题上提供了一种解决途径。根据腐蚀站点提供的腐蚀因子和多项环境数据进行测试,结果表明,该RF-ANFIS模型可以有效实现二氧化硫缺失数据的填补。
2)提出的 RF-ANFIS模型不仅可适用于二氧化硫,可推广至补偿同类型腐蚀因子的缺失情况。
3)充分挖掘了多维数据之间存在的联系和时序数据本身的自相关性,为处理时序数据问题提供了新思路。
4)相关因素分析发现气象上二氧化硫与PM2.5,PM10,NO2三者有紧密的关联性也是一个意外的收获。
[1] 黄海军, 李婵, 王俊. 典型大气腐蚀介质的灰色预测模型分析[J]. 装备环境工程, 2012, 9(1): 13—16. HUANG Hai-jun, LI Chan, WANG Jun. Study on Grey Prediction Model of Typical Atmospheric CorrosionMediums[J]. Equipment Environmental Engineering, 2012, 9(1): 13—16.
[2] 王安东, 陈跃良, 张勇, 等. 基于灰色马尔科夫模型的2A12铝合金腐蚀预测方法研究[J]. 装备环境工程, 2014, 11(6): 22—28. WANG An-dong, CHEN Yue-liang, ZHANG Yong, et al. The Research on 2A12 Aluminum Corrosion Prediction Method Based on Gray Markov Model[J]. Equipment Environmental Engineering, 2014, 11(6): 22—28.
[3] 黄海军, 李婵, 王俊. 典型大气腐蚀介质的灰色预测模型分析[J]. 装备环境工程, 2012, 9(1): 13—16.HUANG Hai-jun, LI Chan, WANG Jun. Study on Grey Prediction Model of Typical Atmospheric Corrosion Mediums[J]. Equipment Environmental Engineering, 2012, 9(1): 13—16.
[4] ZHI Y J, FU D M, WANG H L. Non-equidistant GM(1,1) Model Based on GCHM-WBO and Its Application to Corrosion Rate Prediction[C]// Leicester: Proceedings of IEEE International Conference on Grey Systems and Intelligent Services, 2015: 272—276.
[5] 刘成臣, 徐胜, 王浩伟, 等. 基于灰色模型和神经网络的铝合金腐蚀预测对比[J]. 装备环境工程, 2013, 9(1): 1—4. LIU Cheng-chen, XU Sheng, WANG Hao-wei, et al. Comparative Study of Prediction Models of Aluminum Alloys Based on Gray Model and Artificial Neural Network[J]. Equipment Environmental Engineering, 2013, 9(1): 1—4.
[6] 周立建, 穆志韬, 邢玮, 等. 基于灰色神经网络的有机涂层寿命预测研究[J]. 装备环境工程, 2011, 8(5): 62—66. ZHOU Li-jian, MU Zhi-tao, XING Wei, et al. Study of Service Life Prediction of Organic Coatings Based on Grey Neural Network[J]. Equipment Environmental Engineering, 2011, 8(5): 62—66.
[7] 萧彧星, 吴光海, 孙宁, 等. BP神经网络在碳钢和低合金钢大气腐蚀数据预测中的应用[J]. 腐蚀科学与防护技术, 2011, 23(2): 171—174. XIAO Yu-xing, WU Guang-hai, SUN Ning, et al. Application of Artificial Neural Network on Prediction of Atmospheric Corrosion Data for Carbon Steel and Low Alloy Steel[J]. Corrosion Science and Protection Technology, 2011, 23(2): 171—174.
[8] 邓志安, 李姝仪, 李晓坤, 等. 基于模糊神经网络的海洋管线腐蚀速率预测新方法[J]. 中国腐蚀与防护学报, 2015, 35(6): 571—576. DENG Zhi-an, LI Shu-yi, LI Xiao-kun, et al. A Prediction Method Based on Fuzzy Neural Network for Corrosion Rate of Marine Pipelines[J]. Journal of Chinese Society for Corrosion and Protection, 2015, 35(6): 571—576.
[9] TIAN Y J, LIU Y, CHENG G J, et al. PCA-FNN Based Performance Prediction for Water Injection in Oilfields[J]. Advanced Materials Research, 2014, 909: 410—417.
[10] FU Z N, XIE H W. Wind Speed Forecasting Based on FNN in Wind Farm[J]. Applied Mechanics and Materials, 2014, 651—653: 1117—1122.
[11] GHIASI M M, ARABLOO M, MOHAMMADI A H, et al. Application of ANFIS Soft Computing Technique in Modeling the CO2Capture with MEA, DEA, and TEA Aqueous Solutions[J]. International Journal of Greenhouse Gas Control, 2016, 49: 47—54.
[12] SEIDL D, JANCÍKOVÁ Z, KOŠTIAL P, et al. Exploitation of Artificial Intelligence Methods for Prediction of Atmospheric Corrosion[J]. Defect and Diffusion Forum, 2012, 326—328: 65—68.
[13] 付青文. 基于规则约简的模糊神经网络模型的研究[D].广州: 华南理工大学, 2012. FU Qing-wen. A Research of Fuzzy Neural Network Model Based on Rules Reduction[D]. Guangzhou: South China University of Technology, 2012.
[14] 张小娟. 自适应神经模糊推理系统(ANFIS)及其仿真[J].电子设计工程, 2012, 20(5): 11—13. ZHANG Xiao-juan. Study on the Adaptive Network-based Fuzzy Inference System and Simulation[J]. Electronic Design Engineering, 2012, 20(5): 11—13.
[15] 陈瑞敏, 吴雁, 康文英, 等. 连续雾霾天气污染物浓度变化及天气形势特征分析[J]. 气候与环境研究, 2014, 19(2): 209—218. CHEN Rui-min, WU Yan, KANG Wen-ying, et al. Analysis of Pollutant Concentrations and Characteristics of Continuous Smoggy Weather[J]. Climatic and Environmental Research, 2014, 19(2): 209—218.
Improved ANFIS-based Imputation Method for Missing Data on Atmospheric Corrosion Environment
SHI Ya-nana,FU Dong-meia,ZHI Yuan-jiea,CHEN Min-dongb
(a. School of Automation; b.Institute of Advanced Materials and Technology, University of Science and Technology Beijing, Beijing 100083, China)
ObjectiveTo propose a new method (RF-ANFIS) based on relevance factors and Adaptive Neuro-Fuzzy Inference System to impute missing important environmental data on atmospheric corrosion.MethodsThe relevance degree between missing data and a number of environmental factors was calculated through relevance factors. Factors of high relevance degree were selected; then a relationship model between missing data and environmental factors was built through ANFIS. Finally, SO2data was taken as the specified object to test the model according to atmospheric data of Beijing in 2015.ResultsThe error of mean square of samples in the improved RF-ANFIS model was 0.696 in the best case. The relative error of 13/14 testsamples was within 20%. It was applicable to data analysis of limited samples.ConclusionThe new method effectively improves the accuracy of imputing environmental data in atmospheric corrosion. It is vital to predict atmospheric corrosion rate with missing data.
atmospheric corrosion; missing data; relevance factors; ANFIS
FU Dong-mei(1963—), Female, from Liaoning, Doctor, Professor, Research focus: intelligent data analysis.
10.7643/ issn.1672-9242.2016.06.014
TJ01;TG172.3
A
1672-9242(2016)06-0078-07
2016-07-12;
2016-08-12
Received:2016-07-12;Revised:2016-08-12
国家重点基础研究发展计划项目(2014CB643300);国家科技基础性工作专项(2012FY113000)
Fund:Suported by The National Basic Research Program of China(2014CB643300); The National Science and Technology Basic Work (2012FY113000).
石雅楠(1993—),女,辽宁人,硕士研究生,主要研究方向为大气腐蚀数据挖掘的研究。
Biography:SHI Ya-nan(1993—), Female, from Liaoning, Master graduate student, Research focus: atmospheric corrosion data mining.
付冬梅(1963—),女,辽宁人,博士,教授,主要研究方向为智能数据分析的研究。

