PEP(A)版与IBID版数学教材中平面向量例题难度的比较
濮安山,徐慧敏
PEP(A)版与IBID版数学教材中平面向量例题难度的比较
濮安山1,徐慧敏2
(1.扬州大学数学科学学院,江苏扬州 225002;2.江苏省新海高级中学,江苏连云港 222000)
运用数学题的综合难度模型对中国PEP(A)版和澳大利亚IBID版数学教材中向量一章的例题难度进行比较.发现:(1)IBID版教材数学例题综合难度大于PEP(A)版;(2)在探究、背景、知识含量3个因素上PEP(A)版教材数学例题的难度高于IBID版,而在运算和推理方面IBID版数学例题的难度要高于PEP(A)版;(3)探究因素方面,在识记水平和理解水平上IBID版高于PEP(A)版,但在应用水平和探究水平上PEP(A)版比IBID版高;(4)背景因素方面,两套教材的例题编排都以无背景题为主,有背景题所占比例极小;(5)在运算因素方面,PEP(A)版教材中无运算、数值运算、简单符号运算例题所占比例都高于IBID版,而在运算难度最高的复杂符号运算的题量却比IBID版的要少很多.
教材比较;国际学校;几何;向量;综合难度
1 引 言
2003年,教育部修订高中数学教学大纲,颁布了《普通高中数学课程标准》(实验稿).PEP(The People’s Education Press)版数学教材是人民教育出版社根据《普通高中数学课程标准》(实验稿)编写的教材,包括A、B两版,是目前国内用量最大的[1].IBID版数学高水平教材由澳大利亚IBID出版社出版,被国内国际中学广为利用[2].例、习题的配置是数学教材的重要组成部分,一定程度反映了数学教材编写者的价值取向和编写风格.所以,比较这两种教材中的数学问题是很有必要的.
选取人民教育出版社《普通高中数学课程标准实验教科书(A版)》(2007版)中必修4向量一章内容作为比较对象.之所以选择向量作为比较对象,一是因为两种教材中都有,都独立成章.另外是向量的重要性,向量是近代数学中的重要概念之一,是沟通代数、几何和三角函数的桥梁,是解决某些数学、物理问题的工具,是数学教材中的重要知识.这里主要运用鲍建生教授“数学课程的综合难度模型”比较两种教材向量一章例题的难度,旨在分析编写者对例题设置的意图,为平面向量教材的编写与修订提供借鉴和参考.
2 研究方法
PEP(A)版教材中平面向量的知识安排在必修4第二章,IBID版数学教材平面向量知识在(Ⅱ)第26章.利用“数学课程的综合难度模型”,采用文本质性分析和定量刻画相结合的研究方法.
(1)模型的选择.选择了鲍建生教授的“数学课程的综合难度模型”[3].
该模型由5个因素构成的五边形,这5个因素分别是探究、背景、运算、推理、知识含量,其中的每个因素又都细化为不同的层次水平.这里主要考察5个因素上两种教材例题的水平如何?
(2)题目的选择.例题是教材编者精心选择的,在题目的类型、背景、难度、作用等方面都能体现编者的设计意图.而例题的难度最能反映试题的核心要素,故比较例题的综合难度,就可以全貌地了解例题的状况.
PEP(A)版教材向量一章不同类型数学题的数量统计如表1.

表1 PEP(A)版向量各种类型数学题数量统计
IBID版向量一章不同类型数学题的数量统计如表2.

表2 IBID版向量各种类型数学题数量统计
从上述表格可以看出,两套教材在问题的设置上有着明显的差异,PEP(A)版教材的问题类型丰富,但相对来说数量较少.而IBID版教材无论是例题的数量还是总数都占着明显的优势.问题的数量只能看到表面的现象,要想了解问题的质量还要运用科学的工具对两套教材问题进行更深层的比较.
以上统计的各种类型数学题中只有以“例”、“Example”形式出现的问题是完整给出题干和分析解答过程的数学题.而出现在教材的“探索”、“思考”、“练习”、“习题”、“Exercises”中的数学题只有题干,没有解答过程.对于没有给出完整解答过程的数学题,如果对其做综合难度分析,会使分析结果带有研究者的主观性,降低了研究结果的客观性.所以只选择了教材中的例题作为比较对象.具体题目确定为PEP(A)版37个“例”,IBID版53个“Example”.
3 研究结果与分析
3.1 综合难度
PEP(A)版例题和IBID版例题各难度因素的难度值统计如表3所示.

表3 两套教材例题难度因素对照
根据两套教材各难度因素的加权平均值画出两套教材的数学题综合难度五边形如图1.
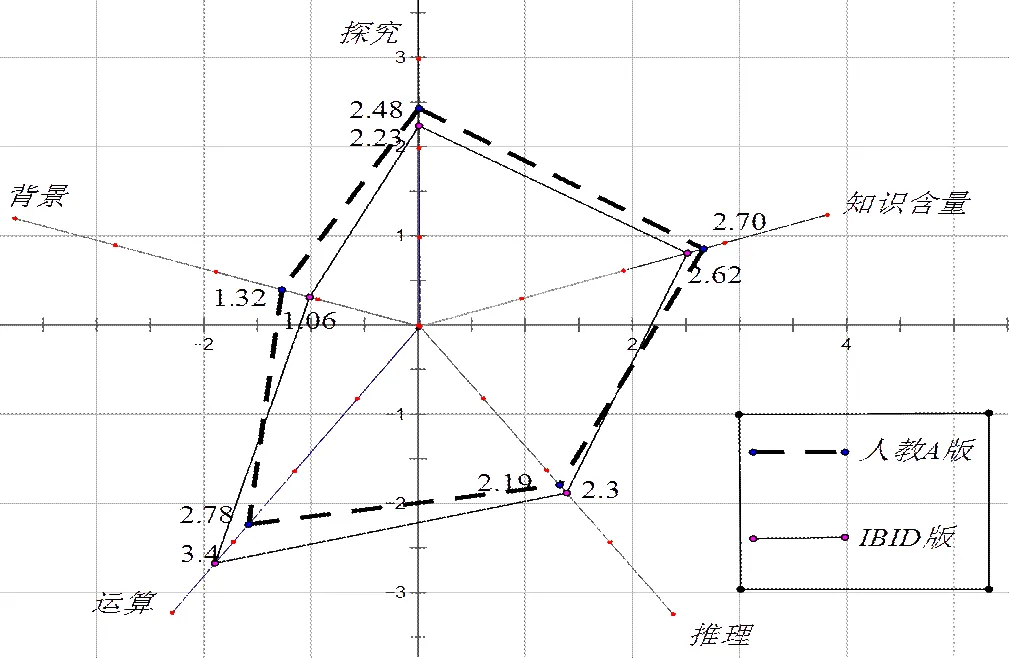
图1 两套教材例题综合难度五边形
这个五边形直观地显示出:(1)在探究、背景、知识含量3个因素上PEP(A)版教材数学例题的难度高于IBID版,而在运算和推理方面IBID版数学例题的难度要高于PEP(A).(2)两套教材的5个因素中,背景因素的难度值相比其他4个因素要小很多,两套教材都特别注重运算,这是由向量自身的知识结构决定的,教材中大量篇幅介绍了向量的加、减、数乘、数量积、向量积运算,其次才是几种运算的应用.(3)两套教材都没有保持5个因素的平衡性,特别是IBID版教材的综合难度五边形向右倾斜的程度要高于PEP(A)版.
探究、背景、运算、推理、知识含量5个因素对应的权重均值分别为1=0.210,2=0.120,3=0.185,4=0.225,5=0.260.PEP(A)版5个因素难度的加权均值为1=2.48,2=1.32,3=2.78,4=2.19,5=2.70,得PEP(A)的综合难度为2.39.而IBID版5个因素难度的加权均值为=2.23,=1.06,=3.40,=2.30,=2.60,得IBID版的综合难度为2.45.,即IBID版教材数学题综合难度大于PEP(A)版数学题综合难度.
3.2 探 究
PEP(A)版教材的37个例题在探究的4个水平上的表现是:识记水平的占16.22%的题量,理解水平的占24.32%,应用水平的占54.05%,探究水平的占5.41%.IBID版教材的53个例题在探究的4个水平上的表现是:探究水平的占22.64%的题量,理解水平的占32.08%,应用水平的占45.28%,探究水平的占0.(如图2所示)
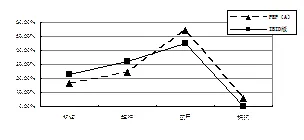
图2 两套教材探究因素各个水平题量折线图
从图2可以看出在识记水平和理解水平上IBID版要求高于PEP(A)版,在应用水平和探究水平上PEP(A)版的要求要比IBID版高,IBID版的数学题并没有体现探究水平,两套教材都相当重视数学知识的应用.这也体现了《普通高中数学课程标准》(实验稿)对于数学课程的要求:“高中数学课程有助于学生认识数学的应用价值,增强应用意识,形成解决简单实际问题的能力.”[4]
3.3 背 景
PEP(A)版教材的37个例题有86.49%无背景题,2.7%是个人生活背景,2.7%是公共常识背景,8.11%是科学背景题.IBID版教材的53个例题有96.22%是无背景题,1.89%是个人生活背景题,1.89%是公共常识背景题,没有科学背景的题.4种类型题的比例所成折线图如图3.

图3 两套教材背景因素各个水平题量折线图
由图3可知两套教材的例题编排都以无背景题为主,有背景题所占比例极小.以上现象可能是由高中阶段学生数学学习方式决定的,高中阶段的学生数学学习方式已经由初中阶段的半抽象、半具体转变为可以依靠完全抽象思维来解决数学问题的程度了.这就使得教材编写者可以直接抽象出问题的关键编写成数学题,而不需要大量的背景铺垫来激发学生的学习热情.PEP(A)版的例题中有8.11%是科学背景的题,这种在例题中渗透科学背景的方式在向量的概念引入时就已体现.而IBID版教材通篇都没有涉及向量和物理等学科的联系.PEP(A)版将向量与物理联系的如此密切印证了《普通高中数学课程标准》(实验稿)对于数学课程的界定:“高中数学课程是学习高中物理、化学、技术等课程和进一步学习的基础.”[4]
3.4 运 算
PEP(A)版教材的37个例题有18.92%是无运算例题,8.11%是数值计算得题目,48.65%是简单符号计算,24.32%是复杂符号.IBID版教材的53个例题有5.66%是无运算例题,39.62%为简单符号运算,54.72%为复杂符号运算,其中数值运算的题目为0.
4种类型题的比例所成折线图如图4.

图4 两套教材运算因素各个水平题量折线图
从图4可以看出,PEP(A)版教材中无运算、数值运算、简单符号运算例题所占比例都高于IBID版教材,而在属于运算难度最高的复杂符号运算的题量却比IBID版的要少很多.PEP(A)版教材例题的运算水平多数集中在简单符号运算,而IBID版教材的例题多数集中在复杂符号运算.两套教材中属于数值运算的例题所占的比例都比其它3种运算难度要少,这是由向量知识的特殊性决定的,在向量学习中发现,向量的加、减、数乘、数量积运算以及坐标运算是不同于以往的简单的数值加减乘除等运算的.在向量的加、减、数乘、数量积、坐标运算中虽然有时不涉及字母未知数,但是它们仍然是属于符号运算的内容.
3.5 推 理
PEP(A)版教材的37个例题有27.03%是无推理例题,27.03%为简单推理例题,45.94%是复杂推理例题.IBID版教材的53个例题有13.21%为无推理例题,41.51%为简单推理例题,45.28%为复杂符号推理.
4种类型题的比例所成折线图如图5.
可以看出,两套教材在推理因素的3个难度水平上的题量呈上升趋势,最高难度的题量最多.PEP(A)版教材的无推理难度的题量约是IBID版教材的两倍,但在简单推理难度上,PEP(A)版教材的题量要比IBID版少,在复杂推理难度上PEP(A)版教材的题量略多于IBID版.PEP(A)版教材的无推理和简单推理两个水平的题量是相同的.两套教材都特别重视解题过程中数学推理的应用,推理是数学思维的核心.
3.6 知识含量
PEP(A)版教材的37个例题中单个知识点的例题占21.62%,两个知识点的占18.92%,3个知识点的占27.03%,4个以上知识点的占32.43%.IBID版教材的53个例题中单个知识点的占11.32%,两个知识点的占15.09%,3个知识点的占26.42%,4个以上知识点的占47.17%.4种类型题的比例所成折线图如图6.

图6 两套教材知识因素各个水平题量折线图
由图6可知IBID版教材4个难度水平上的题量随着难度的增加而增多.PEP(A)版教材4个难度水平的题量整体呈上升趋势,但是两个知识点的题量比单个知识点的题量要少,IBID版教材的4个以上知识点的题量要比人教版的多很多.
4 结论与启示
4.1 结 论
对两套教材给出的数学例题的综合难度分析后得出以下结论.
(1)IBID版教材数学例题综合难度大于PEP(A)版.
(2)在探究、背景、知识含量3个因素上PEP(A)版教材数学例题的难度高于IBID版,而在运算和推理方面IBID版数学例题的难度要高于PEP(A)版;两套教材都没有保持5个因素平衡性,背景因素的难度值相比其它4个因素要小很多,都特别注重运算.
(3)在探究因素方面,在识记水平和理解水平上IBID版高于PEP(A)版,但在应用水平和探究水平上PEP(A)版要比IBID版高,IBID版的数学题并没有体现探究水平,两套教材都非常重视数学知识的应用.
(4)在背景因素方面,两套教材的例题编排都以无背景题为主,有背景题所占比例极小.
(5)在运算因素方面.PEP(A)版教材中无运算、数值运算、简单符号运算例题所占比例都高于IBID版教材,而在运算难度最高的复杂符号运算的题量却比IBID版的要少很多;PEP(A)版教材例题的运算水平多数集中在简单符号运算,而IBID版教材的例题多数集中在复杂符号运算.
(6)在推理因素方面.例题量呈上升趋势,最高难度的题量最多;PEP(A)版教材的无推理难度的题量约是IBID版教材的两倍,但在简单推理难度上,PEP(A)版教材的题量要比IBID版少,在复杂推理难度上PEP(A)版教材的题量略多于IBID版.PEP(A)版教材的无推理和简单推理两个水平的题量是相同的.
(7)在知识含量因素方面.IBID版教材各个水平上的题量随着难度的增加而增多,而PEP(A)版教材4个难度水平的题量整体呈上升趋势,但两个知识点的题量比单个知识点的题量要少,IBID版教材的4个以上知识点的题量要比人教版的多很多.
4.2 启 示
(1)例题的选择应把综合性和特殊性相结合.
研究表明,两套教材都没有保持5个因素平衡性,背景因素的难度值相比其它4个因素要小很多,都特别注重运算.所以,例题的选择和编制应与数学内容紧密结合,充分考虑其特殊性.如向量概念的引入,在5个因素中要特别注重背景知识,把背景嵌入到例题中,增强学生对向量作用的认识.
(2)适当加强例题的运算和推理难度.
研究表明,在探究、背景、知识含量3个因素上PEP(A)版教材数学例题的难度高于IBID版,而在运算和推理方面IBID版数学例题的难度要高于PEP(A)版.运算和推理是数学证明的基础和重要组成要素,运算和推理的难度也一定程度决定了数学问题的证明难度.可能考虑到PEP(A)版教材的应用范围广,要适用于不同省份、不同地区、不同文化背景、不同水平学生的适应性,是可以理解的.建议在原有例、习题的基础上增加一些选作题,在推理与运算的难度上有所增加,用*号加以标注,给学有余力的学生选作.
(3)要注重数学的应用性.
数学应用的广泛性是数学学科一个重要特征.数学教育家弗莱登塔尔很强调学生数学学习要关注数学的现实化.阅读荷兰的中小学数学教材的例、习题的选择和编制可以看出,他们特别注重数学与现实世界的联系,强调问题的现实背景,学生通过数学问题的解决,感觉到数学在现实中有原型,能体会到数学的作用和学习数学的意义.
研究表明,在背景因素方面,两套教材的例题编排都以无背景题为主,有背景题所占比例极小.在新一轮数学课程改革中,中小学数学课程都特别突出了数学应用性理念,高中数学教材中也增加了数学建模的课程.但在实际的数学教学中,例、习题的背景因素和应用性常常被忽略.建议中国中小学数学教材的编写者参考荷兰的数学教材,结合中国的具体实情编制出有一定现实背景、突出数学现实应用的例、习题.
[1] 人民教育出版社.普通高中数学课程标准实验教科书必修(4)[M].北京:人民教育出版社,2007.
[2] Nigel Buckle, Iain Dunbar.[M]. Published by IBID Press, 2004.
[3] 鲍建生.中英两国初中数学课程综合难度的比较研究[D].华东师范大学,2002.
[4] 中华人民共和国教育部.普通高中数学课程标准(实验稿)[M].北京:人民教育出版社,2003.
Comparison about Difficulty of Examples of Plane Vector between the PEP (A) Version and the IBDP Version
PU An-shan1, XU Hui-min2
(1. College of Mathematics Sciences, Yangzhou University, Jiangsu Yangzhou 225002, China;2. Xinhai Senior High School in Jiangsu, Jiangsu Lianyungang 222000, China)
Comparing the difficulty of examples about plane vector in PEP (A) version and IBIDversion mathematics textbook by means of math comprehensive difficulty model. It is found that (1) mathematics problem in IBID version is more difficult than PEP (A) version for the general difficulty of Mathematics; (2) For the three factors of exploration, background, and knowledge content, the difficulty of textbook in the PEP (A) version is higher than it in the IBID version, whereas the performance of difficulty is opposite; (3) In terms of inquiry factors between two sets of textbook: the requirements of IBID in memorizing level and understanding level are higher than that of the PEP (A) version, but the requirements of PEP (A) version in the application level and exploration are higher than IBID; (4) In terms of background factors between two sets of textbook: the most typical problems in the two sets of textbooks are no background layout, problems with background occupies a very small proportion; (5) In terms of operational factors between two sets of textbook: the examples problems in PEP (A) version of the textbook without operation, numerical computation, simple symbolic computation have higher proportion than IBID, but the quantities of problems with the most difficult operation and complex symbolic computation is less than IBID.
textbook comparison; international school; geometry vetor; mathematical difficulty
[责任编校:周学智]
G423.3
A
1004–9894(2016)03–0010–04
2016–01–19
江苏高校品牌专业建设工程资助项目——数学与应用数学(PPZY2015B109);2015年江苏省研究生教育教学改革研究与实践课题——全日制教育硕士研究生教育实习的研究——以学科教学(数学)为例(JGLX15_160)
濮安山(1964—),男,黑龙江安达人,教授,博士,硕士生导师,主要从事数学课程与教学研究.

