天然气黏度精确计算新模型

杨晓鸿 张顺喜 朱薇玲

武汉轻工大学化学与环境工程学院

天然气黏度精确计算新模型

杨晓鸿 张顺喜 朱薇玲

武汉轻工大学化学与环境工程学院

杨晓鸿等.天然气黏度精确计算新模型. 天然气工业，2016, 36(12): 113-118.

天然气黏度是基础而重要的参数，在天然气开采、输送和加工等领域有着重要的理论和应用价值。为了高效、低成本地获得精确的天然气黏度数据，基于气体分子运动论所得黏度、温度和密度关系，建立了计算天然气黏度的新模型和相应的函数关系式，用大量的实验数据对模型参数进行优化后，给出了天然气黏度随温度和密度的变化曲面图。研究结果表明：①天然气黏度随密度以及低密度区域温度的升高而升高；②天然气黏度在高密度区域随温度的升高而降低。新模型精确地预测了9个天然气样本的黏度数据，其计算值与1 539个处于250～450 K、0.1～140.0 MPa区间的实验数据相比，平均相对偏差不超过1.9%；其中，与测量误差小于0.5%的793个实验数据相比，最大相对偏差不超过0.98%。结论认为，与以前的8种计算模型相比，新模型具有方法简单、结果精确、计算快速、可直接计算含有二氧化碳天然气样本的优点。

天然气 黏度 新模型 温度 密度 组成 气体分子运动论 相对偏差 精确计算

实验测量黏度是最直接、最可靠的方法。但是，在实际工程中，天然气的组成、温度和压力值变化范围较大，完全依赖实验方法测定天然气的黏度值难以满足工程计算的需要；加之许多工程现场的实际困难也限制了黏度测量的实施。因此，建立快速、简便、准确的天然气黏度计算模型十分必要。

1 计算模型

天然气的黏度（η）是温度（T）、密度（ρ）和组成（y）的函数，可以表达为：

因为密度和压强（p）可以根据天然气的状态方程相互计算，因而也可以选择压强为自变量，表达为：

创建天然气黏度的计算模型，就是要明确上述函数关系，从而可以根据天然气的其他物性参数来计算天然气的黏度值，方便理论分析和工程应用。为了这一目标，许多学者做了大量、持续的努力。

1.1Dempsey模型

Carr等[1]于1954年创建了计算天然气黏度的两步方法，首先用图版或公式确定在大气压下的黏度值，然后再用另一图表确定其他温度和压强下的黏度。随后，Dempsey[2]拟合了Carr等人发表的黏度图版，得到如下关系式 (Dempsey 模型)：

式中η表示天然气黏度，mPa·s；η表示大气压力1下的天然气黏度，mPa·s；T表示温度，℃；Tr表示无量纲温度；pr表示无量纲压强；γg表示气体相对密度；a0～a15均表示常数。

1.2LBC模型

1964年Lohrenz和Bray等[3]人提出了计算高压气体黏度的表达式：

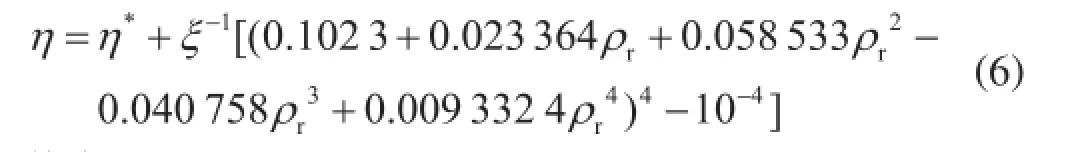
其中

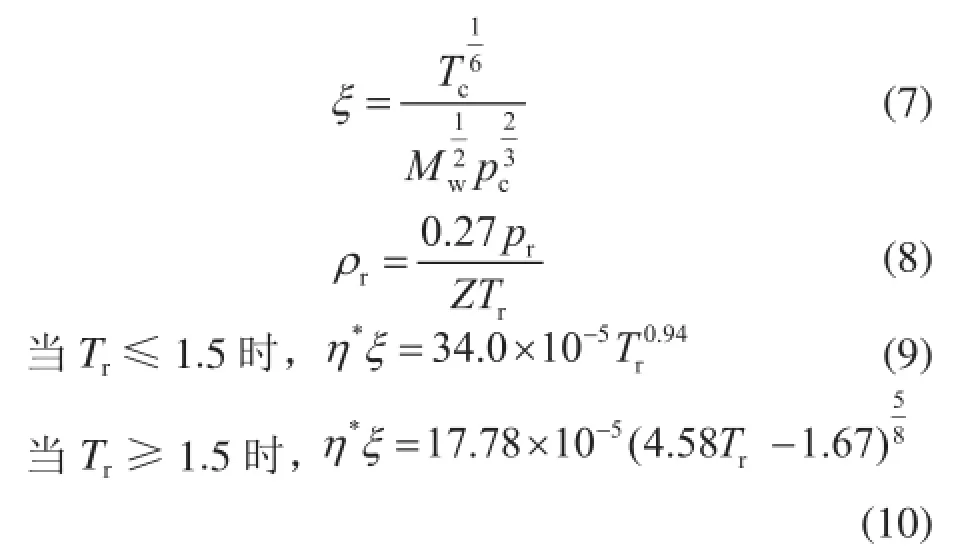
式中η表示待求天然气的黏度，mPa·s；η*表示低压混合气体的黏度，mPa·s；ρr表示无量纲密度；ξ表示混合物的黏度参数；Mw表示天然气的分子量；Z表示天然气的压缩因子。上述计算模型均以低压（零密度极限）气体的黏度为基础，计算高压（或高密度）的天然气黏度值。

1.3LGE模型

1966年Lee等[4]发表了不同风格的计算天然气黏度公式：

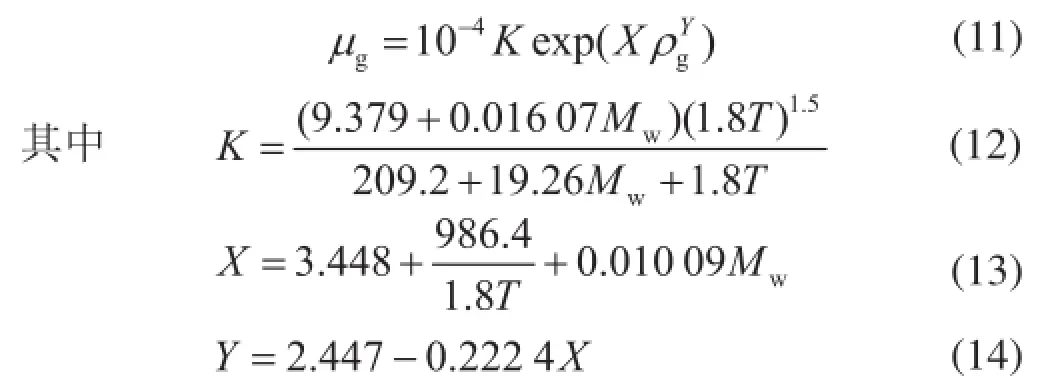
式中ρg表示天然气密度，g/cm3；Mw表示气体分子量；T表示温度，K；μg表示天然气黏度，mPa·s。

1.4Vesovic-Wakeham (VW)模型

1989年，Vesovic和Wakeham[5-6]基于分子钢球模型，考虑分子间弱相互作用，并以自相容的方式引入流体属性，以单组分的低密度黏度为已知量，建立了计算天然气黏度VW模型。该模型首次从分子层面探讨天然气黏度与热力学参量的关系。

2002年Zéberg-Mikkelsen等人[7-8]将天然气黏度拆分为零密度极限黏度（η0）与剩余黏度（Δη）之和，

零密度极限黏度可以取大气压下（理想气体）的黏度；按照经典力学的摩擦定律，剩余黏度表达为：

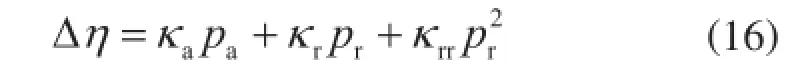
式中pa、pr分别表示van der Waals吸引压强和排斥压强；κr、κa、κrr表示与温度有关的参数。

1.5SLP模型

2011年Sanjari等人[9]基于从实验数据得到的经验，提出如下计算天然气黏度的公式：

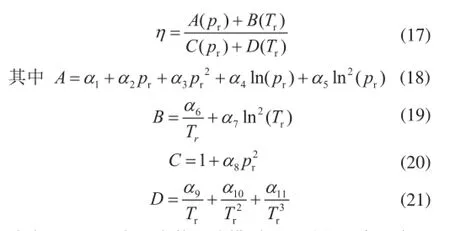
式中α1～α11表示常数。该模型以无量纲温度和为无量纲压强为自变量，可以直接计算黏度。

1.6HEM模型

2013年Heidaryan等[10]通过修订临界温度和压强的表达式，给出如下计算天然气黏度公式：

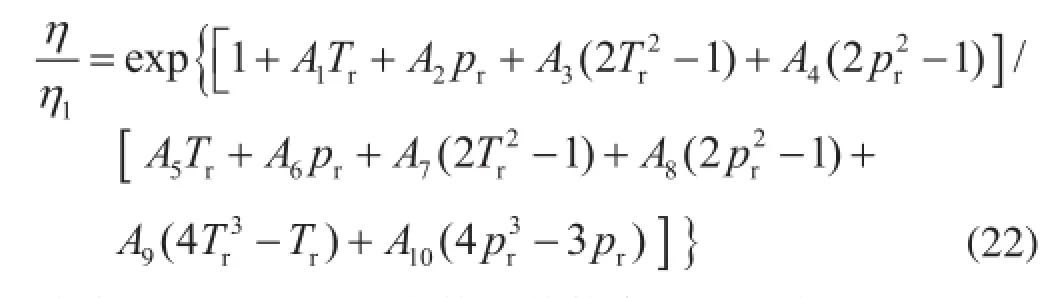
式中A1～A10表示常数，其他变量的定义同前。

1.7JAH模型

2015年Jarrahian等人[11]建议如下计算天然气黏度公式：

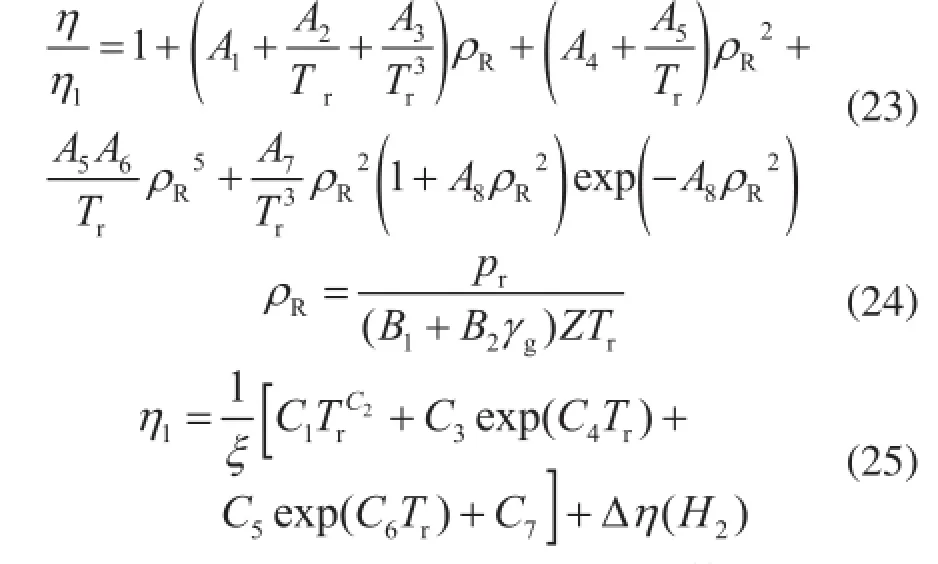
式中A1～A8、B1～B2、C1～C7表示常数。

1.8杨氏理论

上述天然气黏度的计算模型，基本上属于经验或半理论模型。杨等人[12]基于气体分子运动论，建立了天然气黏度与温度、密度关系的新理论。该理论模型的主要内容如下：

天然气的平均临界温度、体积和分子量是其各组分摩尔百分比（yi）的加权平均值，即

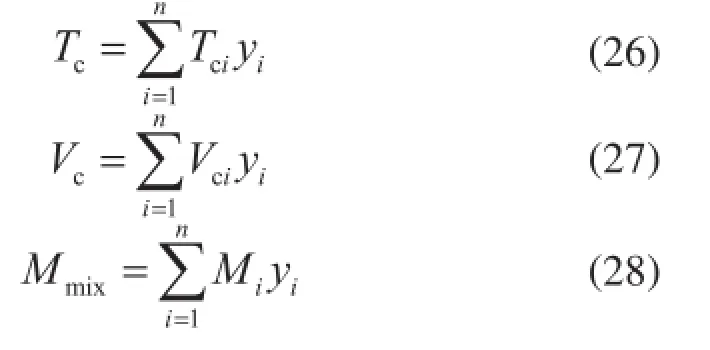
从而，其临界密度为

式中Tc、Vc、ρc和Mmix分别表示临界温度、体积和密度以及平均分子量；Tci、Vci、Mi和yi表示i组分的对应值。以临界参量为基础，可以定义无量纲变量为：

应用无量纲变量，天然气分子的平均吸引能量表示为：

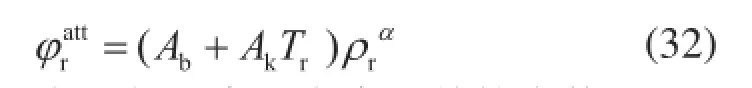
式中Ab、Ak和α表示与温度和密度无关的常数。

最后，天然气黏度的表达式推导成为：

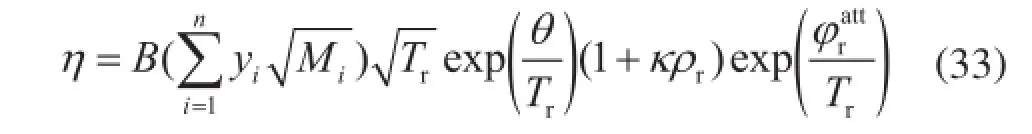
式中B、θ和κ均表示与温度和密度无关的参数。该公式量化地表达了天然气黏度随温度、密度和组成的变化规律。

以上是杨氏理论的主要内容。为进一步简化计算，方便工程应用，可以定义以下变量：

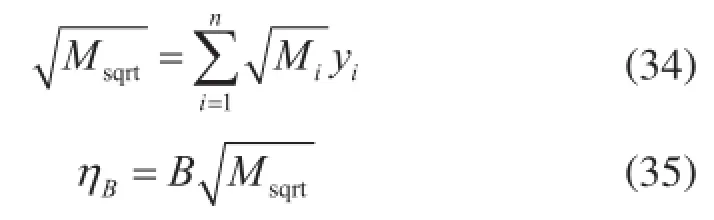
式（34）表示分子量平方根均值，式（35）表示一个与温度、密度无关的黏度参考值。通过适当调整系数，公式中（1+κρr）的变化可以吸收并入指数中，从而得到如下表达式：

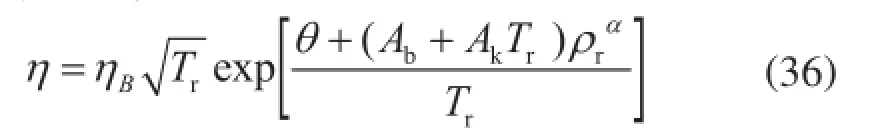
式（36）即为天然气黏度计算的新模型，其参数取值为：B为3.142；θ为-0.551；Ak为0.172；Ab为0.621；α为1.273。这些新优化值可适用于更宽的范围。根据式（36）和参数值、平均临界参数和有关系数与各组分摩尔分数的关系式——式（26）～（29）、式（34）和式（35），天然气黏度随组成、温度、密度的数值变化可方便地在Excel等平台上计算出来。

2 结果与讨论

精选天然气黏度实验数据的来源，如表1所示。图1是参数取前述值时，根据式（36）计算得到的天然气无量纲黏度（ηr）随无量纲温度（Tr）和无量纲密度（ρr）的变化曲面图。由图1可知黏度随密度的升高而升高；在低密度区域黏度随温度的升高而升高，但在高密度区域黏度随温度的升高而降低。

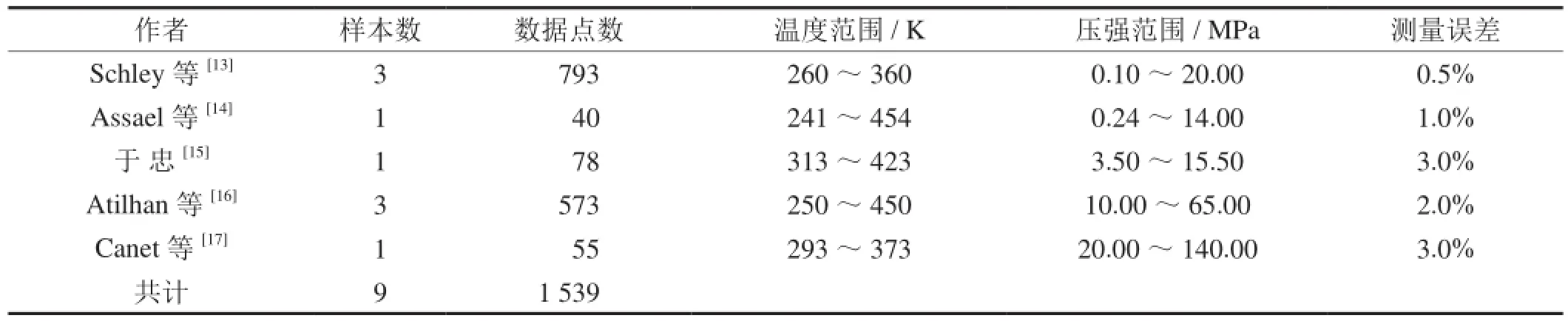
表1 精选天然气黏度实验数据的来源表

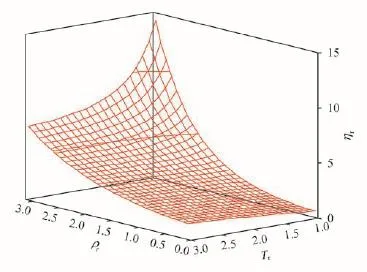
图1 天然气黏度随无量纲温度和无量纲密度的变化曲面图

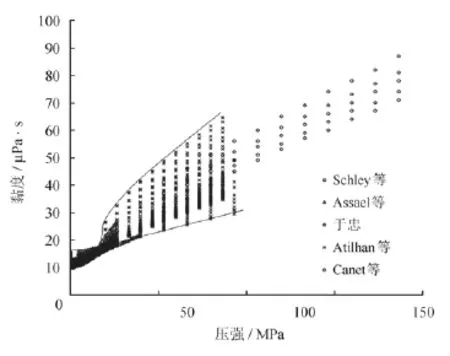
图2 精选1539个天然气黏度实验数据汇总图

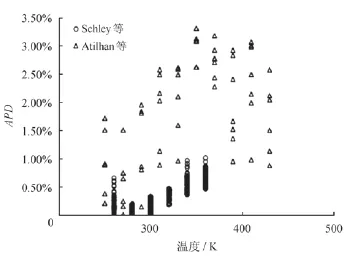
图3 甲烷的APD值随温度的变化图

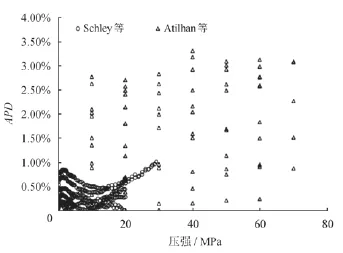
图4 甲烷的APD随压强的变化图

为评价和验证式（36）的正确性，需要收集选取实验数据。精选的原则是：①为新近测量的实验数据，非计算值；②数据来源于先进的实验装置或仪器；③数据之间具有相容性。满足这3项要求的数据源资料收集罗列于表1中，这些2000年以后测得涉及9个样本的总数据点数达1 539，最大测量误差为3%。这些实验数据随压强的变化情况如图2所示。由图2可见，同一样本在不同温度构成的曲线组图形基本相似，不同样本在相同温度不同压强区域的延伸线切合，因而具备相容性。

为量化评价所建立的新模型，定义APD为由式（36）取优化参数时，计算所得预测值与实验数据的相对偏差（APD）为：

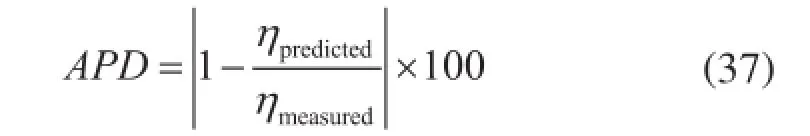
式中ηpredicted、ηmeasured分别表示黏度的模型计算值和实验测量值。

计算甲烷的APD值，其随温度和压强的变化情况如图3、4所示。由图3、4可知，在温度为250～450 K、压强为0.1～70.0 MPa区间，总体上较精确地预测了甲烷的黏度数据，APD的平均值为0.59%，最大值为3.3%。其中，甲烷的APD随温度的增加有所增加，但随压强的变化基本均匀；由于集中在0.1～30.0 MPa区间的Schley实验数据的误差比Atilhan的低，其APD的数据点集中在零点附近的低值区域，表明了总体上APD与实验数据的误差正相关。

其他精选天然气样本的组成如表2所示，以该组成计算所得的主要参数，以及相对1 539个数据点的平均和最大的APD值列于表3。由表3可见，式（36）总体上精确地预测了所列天然气样本的黏度，对1 539个数据点加权平均的APD值为1.9%，最大的APD值为3.1%，其中30 MPa以下计算精度较高，APD值与样本实验数据的误差正相关。

与前人的计算模型比较结果表明（表4），新的计算模型具有简单、精确、计算方便和具备理论基础等优点。

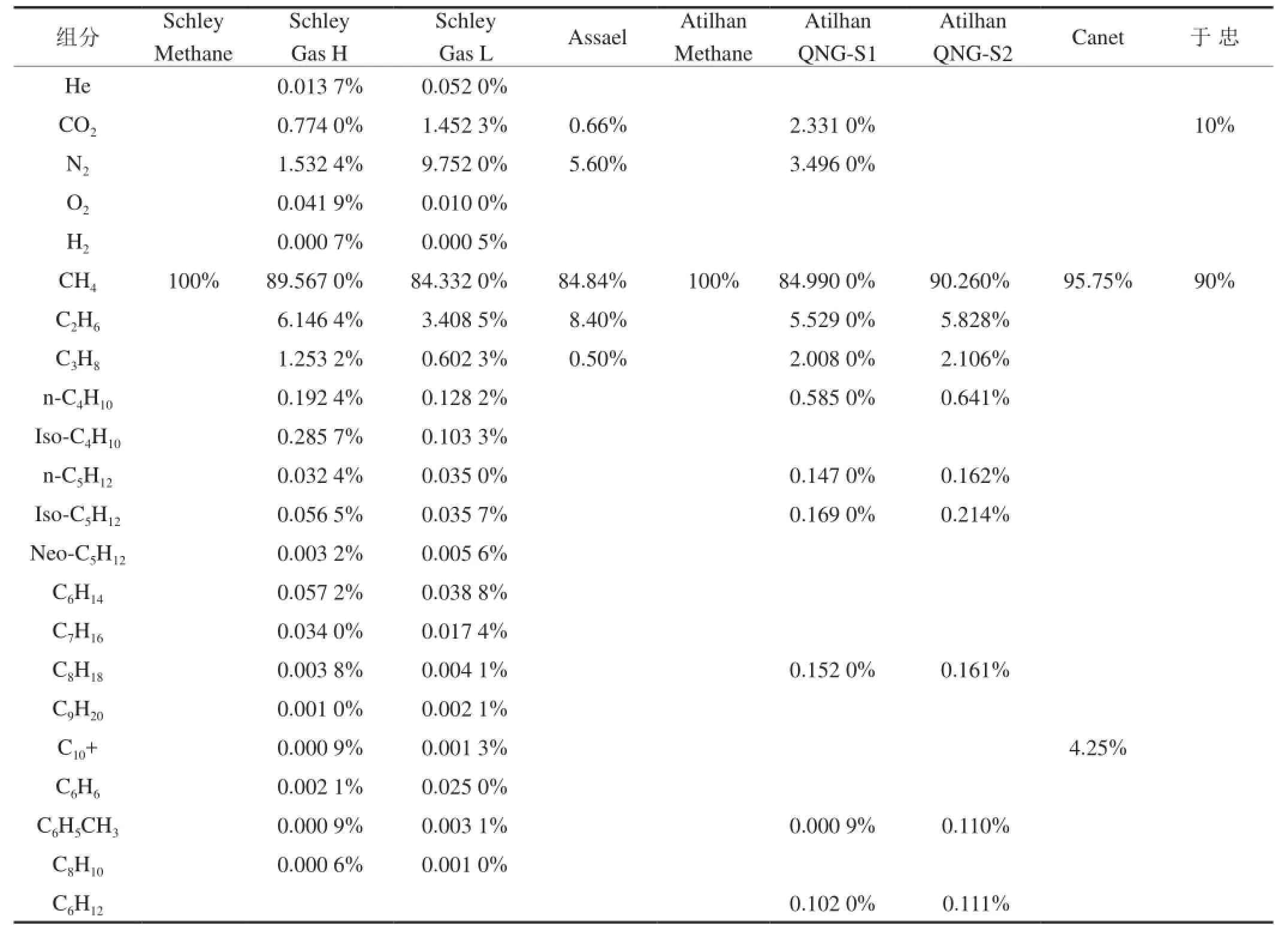
表2 精选9个天然气样本的组成表1)

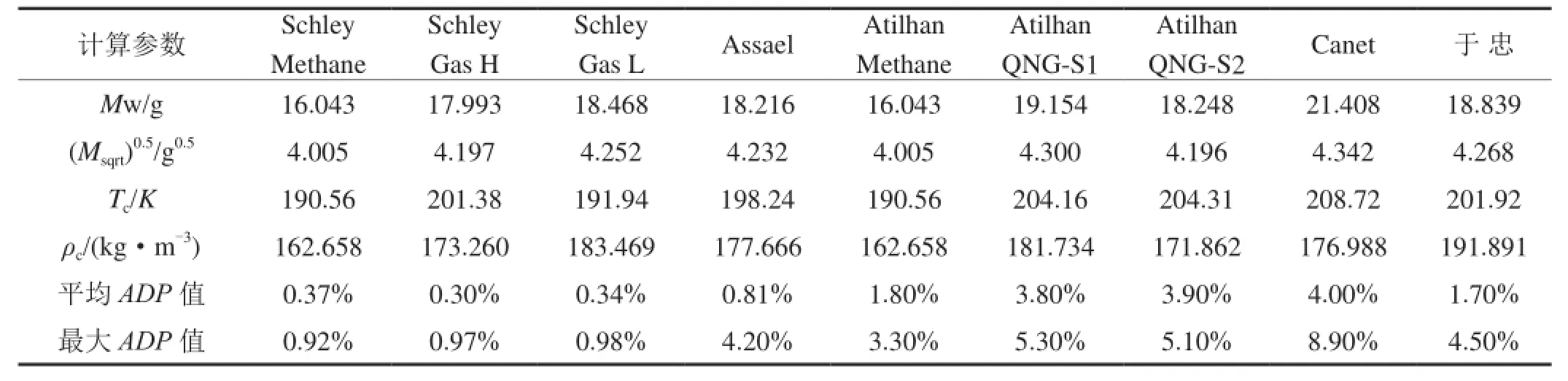
表3 精选9个天然气样本的计算参数和APD值统计表

表4 有关计算模型的APD值和主要特点

3 结束语

基于气体分子运动论所得黏度、温度和密度关系，建立了计算天然气黏度的新模型，该模型量化了天然气黏度与其组成、温度和密度的函数关系。根据该函数，计算了黏度随温度和密度的变化曲面。该曲面表明了黏度随密度以及低密度区域的随温度的升高而升高；但在高密度区域黏度随温度的升高而降低。通过模型的计算值与1 539个位于250～450 K、0.1～140.0 MPa区间的实验数据比较，发现平均相对偏差不超过1.9%；其中，与测量误差小于0.5%的793个实验数据相比，最大相对偏差不超过0.98%。与前人的计算模型比较，笔者报道的新模型具有简单、精确、计算方便、具备理论基础、可以直接计算含有二氧化碳天然气样本等优点。当涉及黏度的分析、计算和设计时，建议在天然气实际工程中应用。

[1] Carr NL, Kobayashi R, Burrows DB. Viscosity of hydrocarbon gases under pressure[J]. JPT, 1954, 6(10): 47-55.

[2] Dempsey JR. Computer routine treats gas viscosity as a variable[J]. Oil and Gas Journal, 1965, 63(8): 141-143.

[3] Lohrenz J, Bray BG, Clark CR. Calculating viscosities of reservoir fluids from their compositions[J]. JPT, 1964, 16(10): 1171-1176.

[4] Lee AL, Gonzalez MH, Eakin BE. The viscosity of natural gases[J]. JPT, 1966, 18(8): 997-1000.

[5] Vesovic V, Wakeham WA. The prediction of the viscosity of dense gas mixtures[J]. International Journal of Thermophysics, 1989, 10(1): 125-132.

[6] Vesovic V. Predicting the viscosity of natural gas[J]. International Journal of Thermophysics, 2001, 22(2): 415-426.

[7] Zéberg-Mikkelsen CK, Quiñones-Cisneros SE, Stenby EH. Viscosity prediction of natural gas using the friction theory[J]. International Journal of Thermophysics, 2002, 23(2): 437-454.

[8] Quiñones-Cisneros SE, Zéberg-Mikkelsen CK, Stenby EH. Accurate density and viscosity modeling of nonpolar fluids based on the 'f-Theory' and a noncubic equation of state[J]. International Journal of Thermophysics, 2002, 23(1): 41-55.

[9] Sanjari E, Lay EN, Peymani M. An accurate empirical correlation for predicting natural gas viscosity[J]. Journal of Natural Gas Chemistry, 2011, 20(6): 654-658.

[10] Heidaryan E, Esmaeilzadeh F, Moghadasi J. Natural gas viscosity estimation through corresponding states based models[J]. Fluid Phase Equilibria, 2013, 354(9): 80-88.

[11] Jarrahian A, Aghel B, Heidaryan E. On the viscosity of natural gas[J]. Fuel, 2015, 150(6): 609-618.

[12] Yang Xiaohong, Zhu Weiling. A theoretical model for the density and temperature dependent viscosity of hydrocarbon gases[J]. Petroleum Science and Technology, 2016, 34(8): 765-770.

[13] Schley P, Jaeschke M, Küchenmeister C, Vogel E. Viscosity measurements and predictions for natural gas[J]. International Journal of Thermophysics, 2004, 25(6): 1623-1652.

[14] Assael MJ, Dalaouti NK, Vesovic V. Viscosity of natural-gas mixtures: Measurements and prediction[J]. International Journal of Thermophysics, 2001, 22(1): 61-71.

[15] 于忠. 超临界酸性天然气密度黏度变化规律实验研究[D]. 青岛: 中国石油大学(华东), 2011.

Yu Zhong. Experimental study on density and viscosity characteristics of supercritical acid natural gas[D]. Qingdao: China University of Petroleum (East China), 2011.

[16] Atilhan M, Aparicio S, Alcalde R, Iglesias-Silva GA, El-Halwagi M, Hall KR. Viscosity measurements and data correlation for two synthetic natural gas mixtures[J]. Journal of Chemical & Engineering Data, 2010, 55(7): 2498-2504.

[17] Canet X, Baylaucq A, Boned C. High-pressure (up to 140 MPa) dynamic viscosity of the methane + decane system[J]. International Journal of Thermophysics, 2002, 23(6): 1469-1486.

（修改回稿日期 2016-09-05 编 辑何 明）

A new model for the accurate calculation of natural gas viscosity

Yang Xiaohong, Zhang Shunxi, Zhu Weiling
(School of Chemistry and Environmental Engineering, Wuhan Polytechnic University, Wuhan, Hubei 430023, China)
NATUR. GAS IND. VOLUME 36, ISSUE 12, pp.113-118, 12/25/2016. (ISSN 1000-0976; In Chinese)

Viscosity of natural gas is a basic and important parameter, and it is of theoretical and practical significance in the sectors of natural gas recovery, transmission and processing. For obtaining the accurate data of viscosity efficiently at a low cost, a new model and its corresponding functional relation were developed based on the relationship among viscosity, temperature and density derived from the kinetic theory of gas. After the model parameters were optimized using sufficient experimental data, the diagram showing the variation of viscosity along with temperature and density was prepared. It is shown that the viscosity increases with the increase of density. Furthermore, with the increase of temperature, the viscosity increases in low density regions, but decreases in high density regions. With this new model, the viscosity of 9 natural gas samples was calculated precisely. The average relative deviation between these calculated values and 1 539 experimental data which were measured under 250–450 K and 0.1–140.0 MPa is less than 1.9%. Compared with the 793 experimental data with a measurement error less than 0.5%, the maximum relative deviation is less than 0.98%. It is concluded that this new model is more advantageous than the previous 8 models in terms of simplicity, accuracy, fast calculation, and direct applicability to the CO2bearing gas samples.

Natural gas; Viscosity; New model; Temperature; Density; Composition; Kinetic theory of gas; Relative deviation; Accurate calculation

10.3787/j.issn.1000-0976.2016.12.016

杨晓鸿，1963年生，教授，博士；主要从事材料化学方面的教学与科研工作。地址：（430023）湖北省武汉市汉口常青花园。电话：（027）83943956。ORCID: 0000-0001-7832-4919。E-mail: yangxhong88 @163.com