基于SVM-GRA-模糊熵的项目组合风险优化

杨菊欢，郑唯唯，段博文

西安工程大学理学院，陕西西安 710048



【电子与信息科学 / Electronics and Information Science】

基于SVM-GRA-模糊熵的项目组合风险优化

杨菊欢，郑唯唯，段博文

西安工程大学理学院，陕西西安 710048

针对交互效应下项目组合风险的不确定性和不对称性特点，构建项目组合风险优化模型．借助支持向量机筛选符合战略目标的项目，利用资源、技术及收益的三角模糊数及其熵值反应不确定性，采用灰色关联度刻画三维不对称交互效应，获得项目组合风险测度．基于模糊规划理论，得到满足期望收益下的项目组合风险优化策略，利用数值模拟验证了方法的有效性．

计算数学；项目组合风险；交互效应；支持向量机；灰色关联分析；模糊熵

近年来，随着社会经济一体化发展，市场竞争越来越激烈，企业为了保持自身的竞争优势，不断增强业务能力，同时为了增加收益并降低风险带来的损失，企业需同时实施多个项目，这就形成了项目组合，其重要性日益凸显，项目组合风险的度量亦备受关注．

1952年，Markowitz[1]构建了收益率的均值-方差(mean variance，MV)金融投资组合模型，从而在最小风险状态下获得最大利润．随后有学者发现项目间的交互效应对于项目组合风险的度量至关重要．杨颖等[2]采用关联性分配矩阵描述项目之间的交互效应；管杜鹃等[3]利用交互效应矩阵描述组合项目的资源、技术和收益之间的交互效应．文献[4-7]从复杂网络、生态位重叠等视角研究具有交互效应的项目组合风险．然而，这些研究均未考虑项目的模糊不确定性．杜先进等[8]利用模糊集理论刻画项目信息的模糊不确定性，并研究项目组合选择优化问题；Bhattacharyya等[9]将收益假定为不确定变量，建立多目标均值-熵-偏度模型，利用不确定性理论将其转化为非线性规划模型．然而，这些研究均未涉及项目之间的交互效应．Hall等[10]只考虑交互效应下项目收益的不确定性，却未考虑项目资源和技术的交互效应以及不确定性．从已有项目组合风险的研究发现，大多研究仅考虑项目信息的不确定性或交互效应，实际上，项目信息不能完全确定，且项目间也普遍存在交互效应．

本研究探讨具有项目资源、技术和收益不确定性及不对称性交互效应的项目组合风险优化问题，通过假设建模，最终获得项目组合风险的最优值及最优组合，Matlab软件的应用提高了组合风险优化效率．

1 交互效应下项目组合风险测度

利用三角模糊数(a, b, c)反应项目的模糊不确定性，由于每个三角模糊数对应一个隶属函数，隶属度越大风险就越小[11]，且项目单独实施时所占资源、技术及收益，必须达到定值a时，才具备实施条件．随着其所占资源、技术及收益的增加，隶属度增大风险减小，当达到定值b时，隶属度最大风险最小，最有利于该项目的实施．之后，随着其所占资源、技术及收益继续增加，即其利用的资源和技术等过多时，不利于项目的实施，对应隶属度减小风险增大，当达到定值c时，就不再实施该项目．部分符号说明见表1．

1.1 匹配战略目标项目的确定

企业战略目标是企业在实现其使命过程中所追求的长期结果．反映了企业在一定时期内经营活动的方向和所要达到的水平．决策者应把有限资源用在对企业战略贡献较大的项目上，故组合中的项目首先需符合企业的战略目标，可用支持向量机(support vector machine，SVM)筛选．

表1 数学符号定义Table 1 Definition of mathematical symbols

(1)

由Lagrange乘子αi优化法将式(1)化为对偶问题，即

(2)

由Kuhn-Tucker(K-T)条件得

(3)

支持向量的αi≠0，最优α*满足

(4)

则最优分类函数为

(5)

其中，最优阈值b*由支持向量通过式(1)求得．

对于非线性问题，用内积核函数K(xi·xj)将非线性问题映射到高维空间线性问题，αi满足的条件及分类函数，将式(4)和式(5)中内积运算用K(xi·xj)代替即可．目前径向基函数对于分类较理想，惩罚参数θ和核参数δ=1/(2σ2)可通过交叉验证法获得[12]．

1.2 风险交互效应的度量

假设通过SVM分类，得到i(i=1,2, …, n)个候选项目，由文献[4]知，项目在e维上具有交互效应．该交互效应是多项目在适应环境和利用资源的实际幅度或潜在能力方面表现出的共同性或相似性[5]．灰色系统理论的研究对象有不确定性．灰色关联分析法(grey relational analysis, GRA)是利用灰色关联度来描述因素间相似程度的方法，由灰色关联度整体性知，当灰色关联因子集中超过2个序列时，灰色关联度有不对称性．故可用e(e=1，2，3分别表示项目资源、技术和收益维度)维灰色关联度度量交互效应．

(6)

项目i和项目j在e上的灰色关联度为

(7)

项目自身无交互效应，故σii=0． 项目间的交互效应可增加或减少项目组合风险，具有方向性，两者可能有相等的灰色关联度，故当项目j的实施，使项目i资源利用率和成功概率增大，且项目产品为增效作用，使项目组合风险小于单项目风险之和时，项目 j对i的e维交互效应为负值，反之取正值．

1.3 项目组合风险的度量

(8)

由式(8)得Shannon模糊熵为

(9)

(10)

由专家评分法可得交互效应风险权重及项目自身风险权重分别为ωσ和ωH． 其中，ωσ, ωH∈[0, 1]，ωσ+ωH=1． 因此，项目组合整体风险水平为

(11)

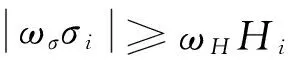
2 项目组合风险优化模型及求解

2.1 构建项目组合风险优化模型

企业实施项目时，总期望利用最小成本获得最大收益，故项目组合收益不能小于项目单独实施时总期望收益，同时需使项目组合风险越小越好．故本研究建模前首先假设：

1)多项目实施时，只考虑两项目间的交互效应，且项目间不存在依赖和互斥关系；

2)交互效应只在资源、技术及收益内部发生；

3)项目资源、技术及收益的模糊值和白化值可通过专家调查法得到．

因此，利用式(11)建模可得

(12)

2.2 模型求解

2)约束条件和目标函数模糊化．不小于约束及目标函数用如下形式表述

(13)

其中，qij为第j个约束条件中自变量xi的系数；ci为目标函数中自变量xi的系数；m为约束条件的个数．

先将约束条件右端视为bj求解，可得目标函数最优值为H0.再用bj+dj代替bj, 可解得目标函数最优值为H0+d0． 各约束条件和目标函数与X上模糊子集Cj和G对应，其中X={x=(x1,x2,…,xn)│xi=0或1}，其隶属函数为式(14)和式(15)．

(14)

(15)

同理可得约束条件为不大于约束时的隶属函数，故模糊约束集为C=C1∩C2∩…∩Cm．

当C(x)≥λ，G(x)≥λ，λ为置信水平，则

(16)

由此可求得其最优解为λ*, 即

D(x*)=∨x∈X(C(x)∧G(x))=λ*

(17)

3 算法流程图

项目组合风险是在不确定性和交互效应的条件下确定的，通过建模得到最佳组合项目及其组合风险．具体过程见图1.

图1 算法流程图Fig.1 The algorithm flow chart

4 算例分析

假设企业现有6个项目，战略目标为S, 分目标S1为降低投入产出比，即项目投入值与项目运行期间每年增加值之和的比值，其值越小经济效益越好，表现为获得物质及资金的渠道和利用率增加，节约人力资源，提高市场占有率、利润率、人员能力和社会影响力等；分目标S2为提高技术，该目标能使技术及其设备得到改进，从而带来更好的经济效益，并使生产效率得到提高．

又由投入产出比及SVM得到候选项目，并进行数值模拟，结果见图2.

图2 SVM分类结果Fig.2 The result of SVM classification

由灰关联软件得σ2=-0.25，σ3=-0.17，σ5=0.06，σ6=-0.16，且有Hi=(0.421, 0.318, 0.150, 0.360)，故可得

minH(x)=0.086x2+0.074x3+0.078x5+0.100x6

(18)

将数值结果与不考虑交互效应时的项目组合风险作对比，此时项目2、3和6的权重为(ωi)1×i=[0.4, 0.3, 0.1, 0.2](i=2, 3, 5, 6)中，去掉项目5的权重后的归一值，即(ω2, ω3, ω6)=(0.44, 0.33, 0.23), 项目组合总体风险水平为H(x)=0.44×0.421+0.33×0.318+0.23×0.36=0.373． 因0.373>0.26，即单独实施比组合实施整体风险水平高，可见考虑交互效应后的项目组合总体风险比不考虑交互效应的项目组合总体风险水平明显降低．故交互效应对项目组合风险的影响不可忽视，正确度量至关重要，并进一步影响到项目组合的选择．

结 语

本研究既考虑了项目组合风险具有不对称交互效应，又考虑了项目信息的模糊不确定性，从而更全面地刻画项目组合风险．研究结果表明，不同类型项目对资源、技术及收益依赖程度不同，只需改变其权重就可适用于不同类型项目．针对企业实际，决策者可制定出符合自身发展的战略目标，即可运用SVM筛选出待选项目．结合GRA及模糊规划理论，可最终获得项目组合风险最优值及最佳组合策略．Matlab程序提高了项目组合风险优化效率，通过算例验证了交互效应对项目组合风险的影响，为决策者选择组合项目规避风险提供了理论参考．

/ References：

[1] Markowitz H.Portfolio selection[J].The Journal of Finance, 1952, 3(7): 77-91.

[2] 杨 颖，杨善林，马 英，等．改进的基于多依赖性的R&D项目组合选择模型[J]．系统工程学报，2011，26(6): 834-841． Yang Yin, Yang Shanlin, Ma Ying，et al.Improved R & D project portfolio selection model based on multi-dependent[J].Systems Engineering,2011,26(6): 834-841.(in Chinese)

[3] 管杜娟，郭 鹏．交互效应及其影响度量下的项目组合关系分类[J]．软科学，2014，28(10)：125-129． Guan Dujuan, Guo Peng.Interaction and influence metric portfolio relationship category[J].Soft Science,2014,28(10): 125-129.(in Chinese)

[4] 管杜娟，郭 鹏.基于脆性联系熵的项目组合脆性风险分析[J]．管理学报，2015，12(10)：1553-1561． Guan Dujuan, Guo Peng.Based on the analysis of brittle link entropy portfolio brittleness risk[J].Journal of Management,2015, 12(10): 1553-1561.(in Chinese)

[5] 赵 静，郭 鹏，潘女兆．基于交互效应的项目组合风险度量及选择优化[J]．运筹与管理，2011，6(20)：121-125． Zhao Jing, Guo Peng, Pan Nv(Nyu)zhao.Based on the interaction effect of portfolio risk measurement and optimization choice[J].Strategy and Management,2011, 6(20): 121-125.(in Chinese)

[6] 郭 鹏，潘女兆，赵 静.基于项目交互效应的高新技术项目组合风险研究[J]．科学与科学技术管理，2009，30(6)：5-9． Guo Peng, Pan Nv(Nyu)zhao, Zhao Jing.Based on the interaction effect of high and new technology project portfolio risk research[J].Science and technology management,2009, 30(6): 5-9.(in Chinese)

[7] 杨 瑞，王安民，张连营．改进的多项目交互组合选择优化模型[J]．工程管理学报，2013，27(6): 71-75． Yang Rui, Wang Anming, Zhang Lianying.Improvement projects more interactive optimization model for portfolio selection[J].Journal of Engineering Management,2013,27(6): 71-75.(in Chinese)

[8] 杜先进，孙树栋，司书宾，等．不确定条件下多目标R&D项目组合选择优化[J]．系统工程理论与实践，2008，28(2)：98-104． Du Xianjin, Sun Shudong, Si Shubin，et al.Under uncertainty multi-target R & D project portfolio selection optimization[J].Systems Engineering Theory and Practice,2008,28(2): 98-104.(in Chinese)

[9] Bhattacharyya R, Chatterjee A, Kar S.Uncertainty theory based multiple objective mean-entropy-skewness stock portfolio selection model with transaction costs[J].Journal of Uncertainty Analysis & Applications,2013, 1(1): 1-16.

[10] Hall N G, Long D Z, Qi J, et al.Managing underper-formance risk in project portfolio selection[J].Operations Research,2014: 660-675.

[11] Ghapanchi A H, Tavana M, Khakbaz M H, et al.A methodology for selecting portfolios of projects with interactions and under uncertainty[J].International Journal of Project Management,2012, 30(7): 791-803.

[12] Wauters M, Vanhoucke M.Support vector machine regression for project control forecasting[J].Automation in Construction,2014, 47: 92-106.

【中文责编：英 子；英文责编：子 兰】

Optimization of portfolio risk based on SVM-GRA-fuzzy entropy

Yang Juhuan, Zheng Weiwei†, and Duan Bowen

College of Science, Xi’an Polytechnic University, Xi’an 710048, Shaanxi Province, P.R.China

A novel project portfolio risk optimization model is proposed based on the uncertainty and asymmetry of the portfolio risk under interactive effects.Specifically, the projects in line with the strategic target are filtered using the support vector machine (SVM).The uncertainty is reflected by the triangular fuzzy number and entropy of portfolio’s resources, technology and benefits.In order to measure the portfolio risk, the three-dimensional asymmetric interactive effect is depicted by employing the grey relational degree.According to the fuzzy planning theory, the optimization strategy which satisfies the expected return of portfolio risk is obtained.Last, the effectiveness of the method is validated by utilizing numerical simulation, and the approach provides a powerful basis for policymakers to measure the portfolio risk and choose the appropriate project portfolio.

computational mathematics; portfolio risk; interactive effect; support vector machine (SVM); grey relational analysis (GRA); fuzzy entropy

O29；F272.3

10.3724/SP.J.1249.2016.06586

国家自然科学基金资助项目(71272049)

杨菊欢 (1991—)，女，西安工程大学硕士研究生．研究方向：计算数学．E-mail:1127354462@qq.com

引 文：杨菊欢，郑唯唯，段博文．基于SVM-GRA-模糊熵的项目组合风险优化[J].深圳大学学报理工版，2016，33(6)：586-592.