基于Matlab/Simulink的三弹簧谐振子微振动的仿真实验

张 林

(南京林业大学，江苏 南京 210037)

基于Matlab/Simulink的三弹簧谐振子微振动的仿真实验

张 林

(南京林业大学，江苏 南京 210037)

建立了三弹簧振子耦合系统微振动的实验模型，利用Matlab/Simulink仿真软件对该实验进行仿真建模，讨论系统在不同实验参数下从周期振动到混沌的各种动力学状态。仿真实验结果表明，参数的选取对系统微振动的动力学行为有着很大的影响。

谐振子；微振动；Simulink仿真

在物理实验教学中，一维弹簧谐振子的微振动是学生认识客观世界复杂振动的起点和基础。在无外力作用时，单个弹簧振子在平衡位置附近做简单的周期性无阻尼振动，而对于多个弹簧振子组成的耦合系统，其微振动在不同参数下可表现为周期振动、准周期振动以及无规则振动(混沌)，因此多个弹簧振子耦合系统的微振动引起了人们广泛的研究兴趣。文献[1]首先使用了Matlab软件对三自由度的微振动进行了计算和讨论，并模拟了系统的动力学过程。随后文献[2-6] 分别使用数值计算和虚拟仿真等方法对多个弹簧振子耦合系统的复杂振动进行了较深入的研究。

为了让学生更好地认识到多弹簧耦合振动的复杂性和可调制性，本文建立了一个三弹簧振子耦合系统的实验模型，并利用Matlab/Simulink仿真软件讨论了不同实验参数对系统微振动状态的影响。

1 一维弹簧振子系统微振动实验的simulink建模

建立如图1所示的一维三弹簧振子的实验系统：三个弹簧振子的质量均为m，弹簧的劲度系数分别为k1、k2和k3，三个谐振子在微振动过程中相对自身的平衡位置的位移分别为x1、x2和x3，取x1，x2和x3为广义坐标，则系统的动力学方程可表示为：

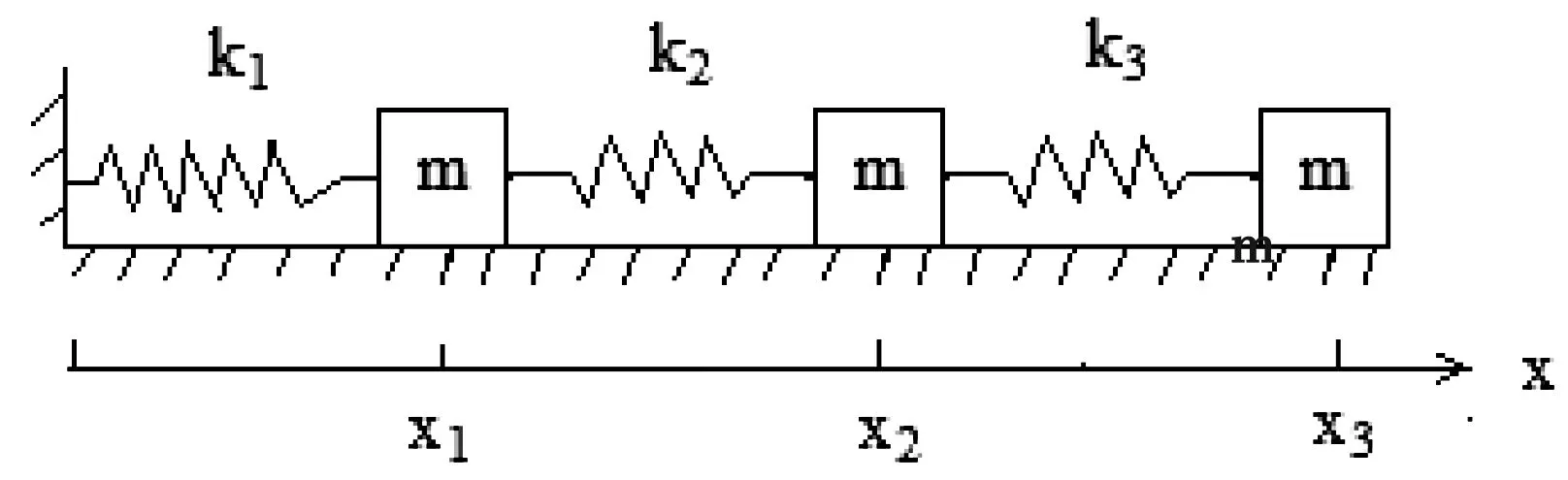
图1 一维三弹簧谐振子系统微振动实验的示意图

(1)

t=0时刻，系统的初位置和初速度分别定义为：

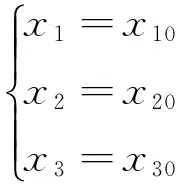
(2)

要得到系统在不同实验条件下的动力学方程，就必须求解上述的二阶常系数微分方程组，我们是通过建立Matlab/Simulink仿真模型来求解系统的微振动状态。

为了简化模型、减少参数，我们将方程组(1)式改写为：

(3)

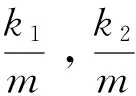
图2 一维弹簧三振子系统的SIMULINK仿真框图

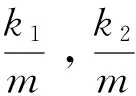
最后，在利用积分模块Integator得到速度方程v和振动方程x的同时，必须对三个弹簧振子的初始速度v0和初始位置x0进行预先设置，具体可以双击积分模块，就可以得到如图3所示的对话框：只要设置其中初始条件Initial condition，就可以设置三个弹簧振子的初始速度和初始位置。

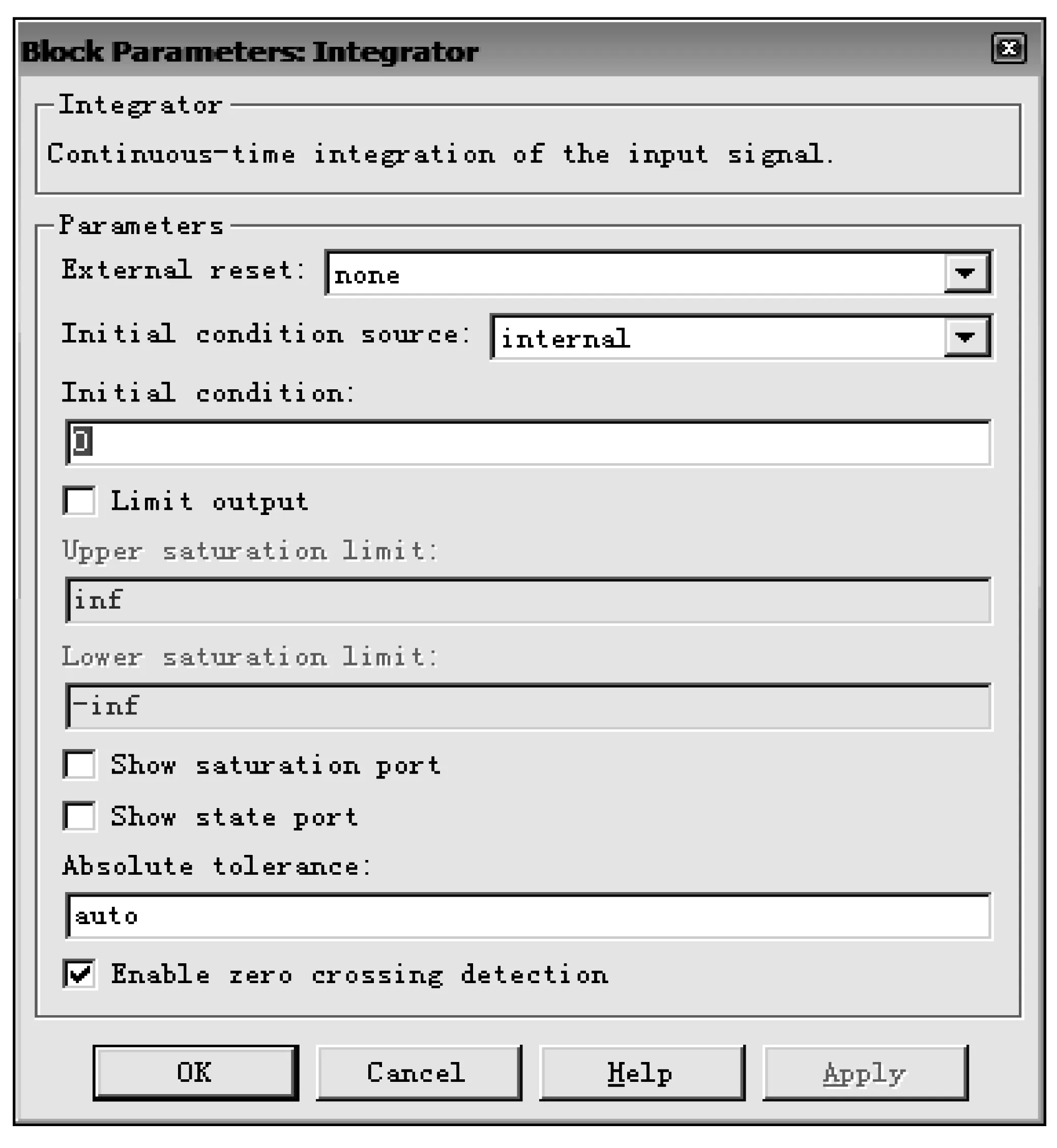
图3 三个弹簧振子初始条件的设置

2 结 论

本文模拟了三个相同质量的弹簧振子的微振动实验，并设定其质量m=1 g；假定t=0 s，三个弹簧振子都处于静止状态，即v10=v20=v30=0 cm/s；第一个和第二个弹簧振子处于各自的平衡位置，即x10=x20=0 cm，假定第三根弹簧被拉伸的长度为1 cm。只要运行仿真软件，打开虚拟示波器Scope，就可以得到在不同的劲度系数k下，三个弹簧振子的振动状态。

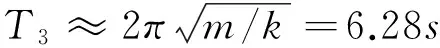
图4 k1=k2=100dyn/cm≫k3=1dyn/cm时，三个弹簧振子的振动曲线

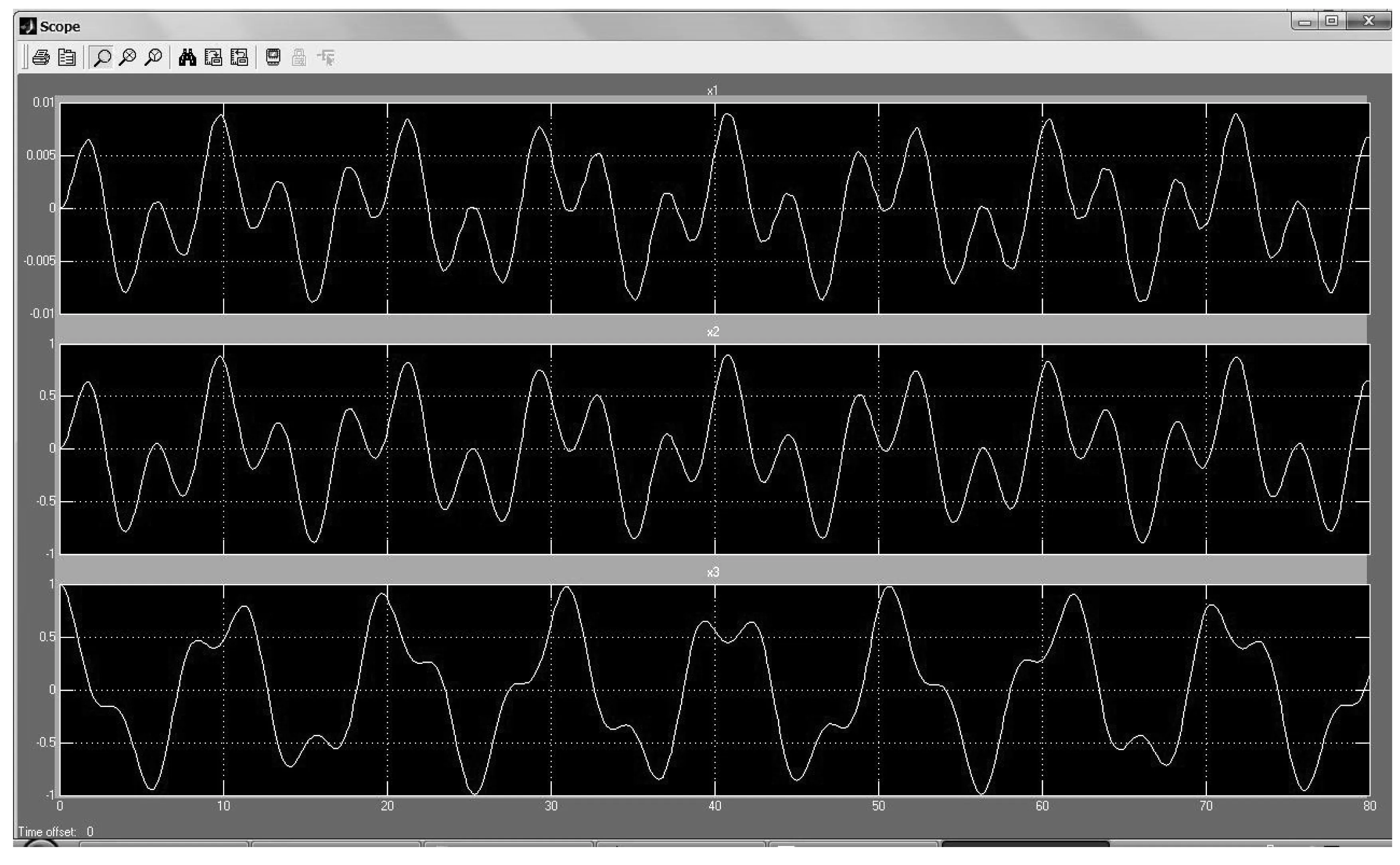
图5 k1=100dyn/cm≫k2=k3=1dyn/cm时，三个弹簧振子的振动曲线

图5是k1=100dyn/cm≫k2=k3=1dyn/cm的情况下，三个弹簧振子的振动曲线。从图中的振动强度可以看出：第一个振子做小振幅振动，而第二个和第三个振子做大振幅振动．三个振子都近似做准周期振动，并且振动周期近似是相等的。另外，从图中可以看出第一个振动和第二振动具有相同的相位，是“同步振动”；而它们与第三个振动“反相”；这时可以近似看成第一个振子不振动，第二个和第三个振子都做自由振动，系统的自由度为2。

图6是k1=k2=k3=1dyn/cm时，三个弹簧振子的振动曲线。从图中的振动强度可以看出：三个振子都做大振幅振动．三个振子的振动表现出为更大的无序性，这种无序性可以从三个振动的相位可以看出: 除了初始时刻，从图中已不能看出三个弹簧振子的振动步调。这时三个振子都做自由振动，系统的自由度为3[7-8]。

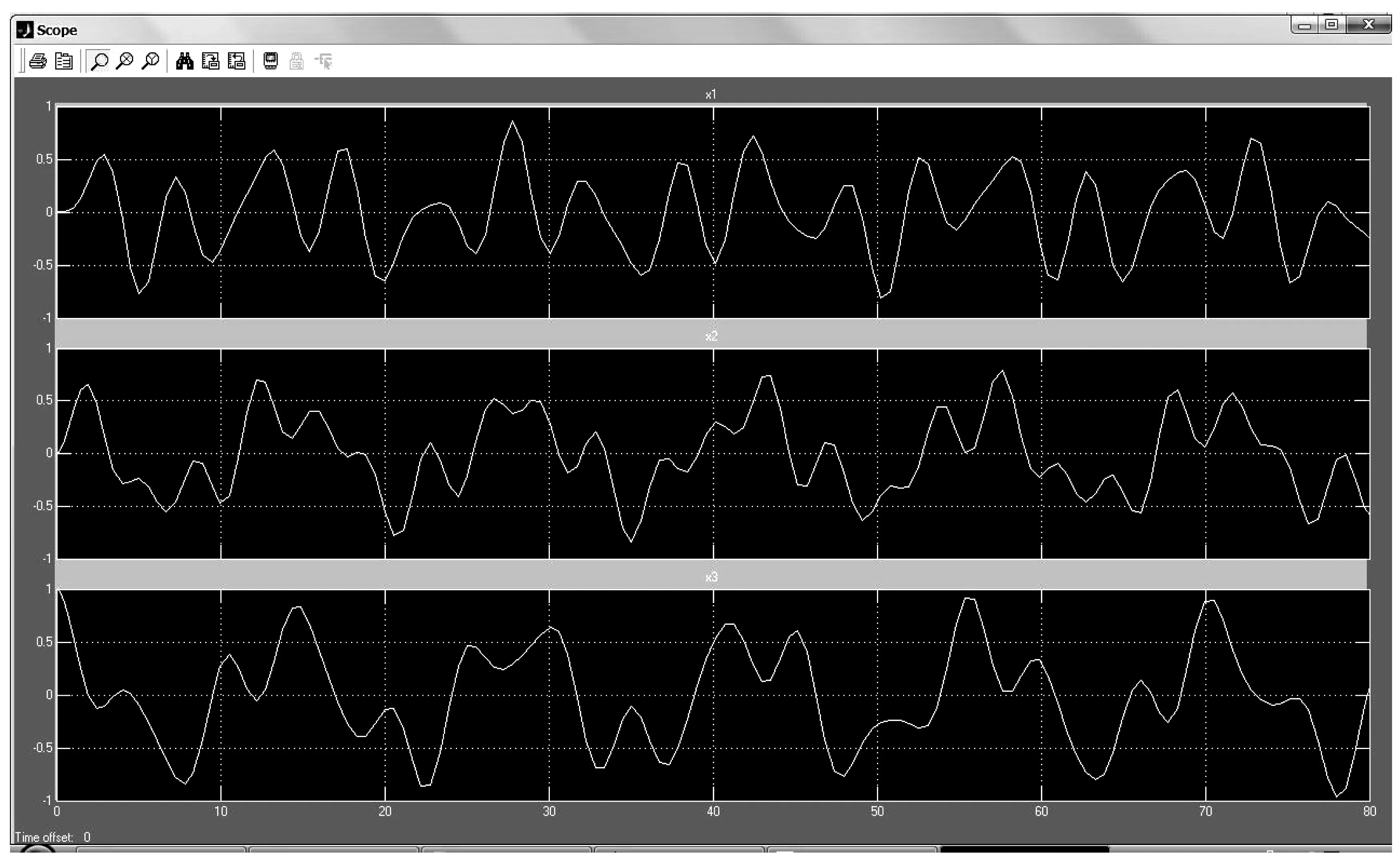
图6 k1=k2=k3=1dyn/cm时，三个弹簧振子的振动曲线

[1] 彭芳麟，胡静，管静，卢圣治． 用Matlab解决线性三自由度系统微振动问题[J]．大学物理，2001，20(11)：31-34.

[2] 林继成，何龙庆，石冰． 多自由度系统的微振动的SIMULINK仿真建模[J]． 安庆师范学院学报，2005，11(4)：18-20.

[3] 陈刚，阮中中．对称多振子系统的振动解耦分析及简正振动频率[J]．物理与工程，2008,18(6)：2-3.

[4] 杨正波，夏清华，刘思平． 多弹簧振子耦合系统运动研究[J]． 大学物理，2010,29(4)：29-32.

[5] 刘建国，张玉芳．对称性耦合双振子的复杂运动[J]．河北大学学报:自然科学版，2012，32(2)：144-147.

[6] 高明杰，高志勇，张雅芳．转动非惯性系中双自由度弹簧系统的运动规律探讨[J]．大学物理，2013，32(3)：37-38.

[7] 徐春芳.基于MaTLaB的多光学现象仿真可视化设计[J].大学物理实验，2016(4)：33-37.

[8] 郑君刚.大学物理实验数据处理中Matlab应用[J].大学物理实验，2015(12)：77-79.

The Simulation Experiment for Three Spring Oscillators’ Micro-vibrations by Using Matlab/Simulink Software

ZHANG Lin

(Nanjing Forestry University,Jiangsu Nanjing 210037)

An experimental model of three spring oscillators’ micro-vibrations is constructed by using Matlab/Simulink software.The different vibrations of the system are also discussed in different experimental parameters from the periodic motion to the chaos.Simulation results show that the selected parameters have great influences on the micro-vibration behaviors of the system.

spring oscillator；micro-vibration；Simulink simulation

2016-07-14

江苏省现代教育技术研究课题(2013-R-25643)

1007-2934(2016)06-0103-05

O 4-39

A

10.14139/j.cnki.cn22-1228.2016.006.028