一种基于通信网络的相继故障模型研究*

刘笑辰，朱 磊，夏 苏

(解放军理工大学 通信工程学院,江苏 南京 210007)

一种基于通信网络的相继故障模型研究*

刘笑辰，朱 磊，夏 苏

(解放军理工大学 通信工程学院,江苏 南京 210007)

大规模通信网络的拓扑结构具有复杂网络的特性，而相继故障现象作为复杂网络中固有的存在，对网络的可靠性带来了严重的威胁。针对通信网络的特点，提出了一种新的相继故障模型——双限制相继故障模型。利用该模型，首先研究网络的初始效率对其健壮性的影响，发现在一定范围内网络健壮性随着初始效率的增加而降低。其次，研究网络中重要性能参数对其健壮性的影响，重点研究了路由器数据转发速率和缓存空间大小对相继故障规模的影响，并且根据实验结果给出了构建通信网络时的若干建议。

通信网络；相继故障；网络健壮性；路由器

0 引 言

通信网络在人们生活中发挥着非常重要的作用，然而相继故障现象的存在对网络的安全性和可靠性造成了严重威胁[1-2]。因此，需对通信网络中的相继故障问题进行研究，找到控制其发生或抑制其危害的方法。

研究相继故障现象，首先要构建相继故障的模型，进而提出一些控制措施。对于复杂网络相继故障的研究最早开始于Albert等[3]，他们对无标度网络中的相继故障现象进行了仿真分析。Motter等[4]最先引入容量和初始负载的线性关系，提出了具有开创性意义的ML模型。Crucitti等[5]则同时考虑节点和边的动态行为，提出了基于边上传输效率动态更新的模型——CLM模型。该模型中，节点过载后并不立即被删除，而是降低与该节点相连的边的传输效率。此后，大量学者对相互作用的复杂网络的相继故障现象进行了分析研究[6-8]。

当前，复杂网络中的相继故障模型大多针对抽象网络。虽然这些模型具有比较广泛的适用性，但是不能完全反映实际通信网络的特征。本文将通信网络映射成一个复杂网络，并且对网络中的节点和边赋予通信网中特有的属性。基于此网络基础，对相继故障过程进行建模分析，以研究通信网络中该现象的规律，寻找增强网络健壮性的方法。

不同网络中引起网络节点或连边发生故障的原因各不相同。在通信网络中，除去网络设备被物理损坏外，网络中的拥塞现象也能够引发相继故障，且后者的发生状态更加隐蔽，造成的后果也更加恶劣。因此，建模过程中将重点研究网络拥塞这一因素对通信网络的影响，提出一种新的相继故障模型——双限制相继故障模型。

1 双限制相继故障模型

1.1 网络模型的构建

由于通信技术的飞速发展，无论规模还是连接的复杂性，当前的通信网络都变得异常复杂。传统的描述方式（总线型、星型、环形等）已经无法描述网络拓扑结构，而采用复杂网络理论可以对网络的拓扑结构进行良好的描述。按照文献[2]所述，通信网络具有小世界特性和无标度特性。因此，本文使用同样具有此特性的BA-无标度网络[3]作为通信网络的拓扑结构。

假设存在一个网络自治域，将其映射成网络G(V,E)。其中，网络中某个节点为vi，其与实际通信网络中的路由器相对应。对于一个通信网络而言，路由器在网络中发挥着核心功能，因此本文重点针对该设备进行建模。对于路由器而言，其最基本的功能是数据的转发和存储。因此，在网络模型中分别采用不同的参数来描述路由器的这两种功能。定义节点的转发能力为ci，表示该节点在单位时间内最多能够向其他节点转发的数据量，并与路由器的转发功能相对应。定义节点缓存空间大小bi，表示该节点在同一时刻最多所能存储的数据量，与路由器的存储功能相对应。

对于节点vi，定义转发负载li，表示该节点在单位时间内需要转发的数据量。当该节点发生拥塞时，有li＞ci，且当该节点缓存区有可能被占满时，在该节点的缓存队列中将按照某种队列调度算法丢弃一些数据包。网络中某个节点发生拥塞，将可能导致整个网络的通信效率下降。因此，研究通信网络中的相继故障现象时，必须要同时考虑节点的转发状态以及缓存区内的队列调度情况，即网络中的节点同时受到这两个因素的限制。

由于技术、经济等方面因素的限制，节点的转发能力和缓存空间长度要受到限制。根据文献[3-4]，令：

式中，li0为该节点的初始负载；α为节点的转发容差，是一个正的常数，在不同网络中有不同的取值。节点的转发容差体现了该路由器应对网络突发流量的转发能力。取值越大，说明路由器应对异常情况的能力越强。同理，参数β同样是一个正的常数，称为节点的缓存容差，体现了该路由器应对网络突发流量的存储能力。可见，式（1）和式（2）分别体现了对节点的转发能力和存储能力进行的限制。

假设网络中节点vi与vj之间的连边为eij，定义边的传输效率λij，表示该连边单位时间内成功传输的数据包数量。根据文献[9-10]，对边的初始传输效率有以下关系：

式中，λij0表示网络中连边的平均初始传输效率，ki表示节点Vi的度，θ是一个随着网络的不同而变化的常数，其对网络的传输效率进行限制。

结合上述表述，将通信网络进行抽象，结果如图1所示，图中对各性能参数进行了标注。

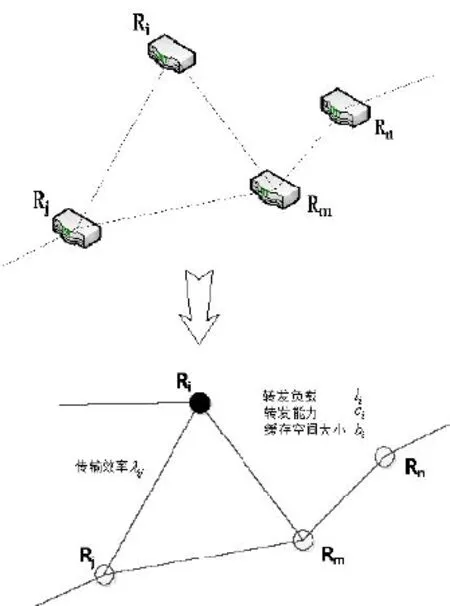
图1 通信网络抽象过程

通过简化抽象，本文建立了一个具有复杂网络拓扑结构的通信网络，并通过一些重要参数描述了抽象网络的特征。下文将对这些参数的作用进行研究。

1.2 相继故障作用机理

复杂网络存在相继故障现象，即网络中极少数节点或边发生故障，就可能引起整个网络发生大规模崩溃。在大部分相继故障模型中，当某个节点的负载超过其容量后，该节点就会被移除网络。但是，在通信网络中考虑到拥塞的影响，当一个节点发生过载时并不应该将其从网络中移除。更实际的情况是，过载的节点按照一种小于正常状态的效率工作。

在本文提出的双限制相继故障中，重点研究网络路由设备由于拥塞而导致的变化，以及对整体网络的影响。

为便于研究，在模型中做出如下假设：

（1）在理想情况下，网络中的每一个节点都按照相同的速率向其他节点自由地发生数据包；

（2）与网络状态变化相比，网络路由表的更新时间忽略不计；

（3）网络中的发送方不执行拥塞控制协议。

根据假设（1）可知，网络中任何一对节点间数据传输速率都是相等的。假设该速率为υ，则对于网络节点vi，其负载即单位时间内需要转发的数据量：

式中，pi表示节点s与d之间通过节点vi发送信息的概率，υsd为s与d的信息传输速率。由网络介数定义[11]可知，pi等于该节点的介数。于是，可得：即网络中节点的负载与其介数成正比，其比例系数为节点间的数据传输速率。

网络运行过程中，由于某种原因（设备老化、人为破坏等），t时刻某一个或几个节点发生损坏。假设这种损坏将导致设备完全不可用，则将代表这些设备的节点从网络中移除。在网络发生初始故障后，网络中的路由器将根据某种路由算法更新设备中的路由表。由节点负载定义可知，这会使网络中相关的节点负载重新分配。对于网络节点vi，在t+1时刻的负载变化为：

式中，li(t)表示节点原有的负载，Δli(t)为由于路由情况变化而导致的负载变化量。当由于负载的变化导致该节点发生过载现象，即li(t+1)＞ci时，说明节点vi由于连锁反应也发生了故障。

显然，连锁反应导致故障节点并没有完全失去功能，因而并不应该将故障节点从网络中移除。实际情况中，当一个路由设备对数据的转发速率小于到达速率时，更可能的结果是一部分未被转发的数据包暂时存储于缓存区中。当缓存空间不足时，不可避免地将导致部分数据包被丢弃。这意味着传递被丢弃包的链路能够正确传送数据包的数量将会减少，以致该链路的传输效率下降。因此，可以将过载对网络节点的影响等效到与过载节点相连的边上，即

式中，λij(t)表示边eij在时刻t的传输效率，pi(t)表示由于节点vi过载导致传输效率下降的因子，其表达式在下文中叙述。

在CLM模型中[6]，pi(t)与过载节点的负载成正比，与其转发能力成反比。但是，在通信网络中，这种笼统的计算方法无法描述链路传输效率的下降情况。对一个路由设备而言，过载现象的产生可导致其缓存区内的数据包被丢弃。假设在缓存区内执行的队列调度算法为尾部丢弃（Tail-Drop）[12]，即当队列长度超过缓存空间的大小时，就将最尾端的数据包丢弃。在这种情况下，可以用排队论对缓存队列进行建模。

模型中，假设数据包的大小都是一致的且长度为L。对节点vi而言，其负载为li(t)，则单位时间内该节点接收的数据包数量为：

当节点vi发生过载时，节点将会按照其最大能力转发数据，因此单位时间内处理的数据量即其转发能力值。于是，单位时间内能够处理的数据包数量为：

节点缓存区的大小为bi，即该节点能够最多容纳bi个数据包。当数据包的到达和离开服从泊松分布时，有排队论中的M/M/1/k模型可知[13]，缓存区在时刻t为空的概率为：

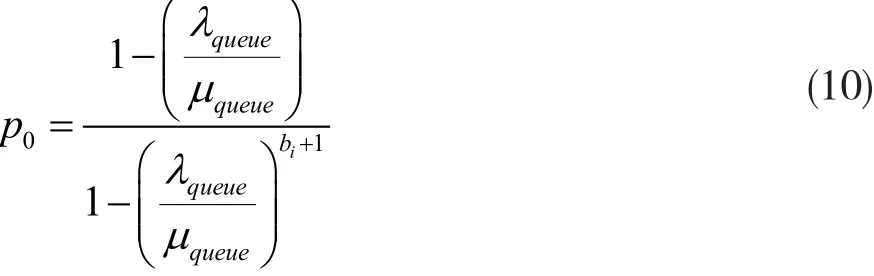
因此，系统到达饱和的概率，即节点发生丢包的概率为：

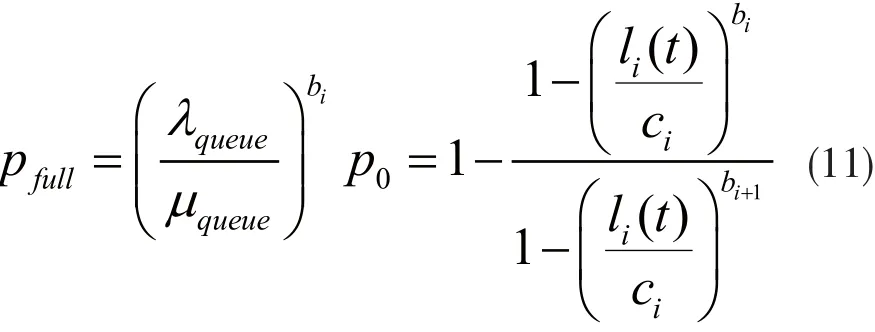
当节点的负载小于其转发能力时，可以忽略数据包被丢弃的情况。因此，pi(t)可以被计算为：

式中，ki为节点i的度。除以节点的度则表示被丢弃的数据包等可能地来自于与该节点相连接的链路。

在t+1时刻，路由表按照链路中新的传输效率值进行更新。这有可能进一步引发新的节点发生过载现象。该过程一直循环往复下去，直到网络重新达到稳定状态或者完全崩溃。

2 仿真结果分析

2.1 随机故障与蓄意攻击对比

通信网络中的随机故障指由于某些偶然的原因导致网络中的某一个或几个节点发生损坏，通常这些节点的度数或负载都是完全随机的。而蓄意攻击指出于某种目的，着重对网络中度数或者负载较大的节点进行毁伤。图2记录了两种攻击对网络的影响。图中横坐标表示相继故障进行的步数，纵坐标表示网络的平均传输速率[14]。其中，网络由1 000个节点组成，实验中令转发容差α=0.2，缓存容差β=20，参数θ=1。针对不同的攻击，令初始故障节点的数目均为5。实验结果取10次以上平均值。

从图2中可以看出，在同一个网络中，由蓄意攻击引发的相继故障平均传输效率值约下降35.3%，而由随机故障引发的相继故障造成传输效率值下降了约20%，即蓄意攻击容易引发更为严重的后果。该结果与文献[5]和文献[15]中的相继故障模型具有的性质保持一致。可见，增强网络的可靠性必须注意保护网络的关键节点。

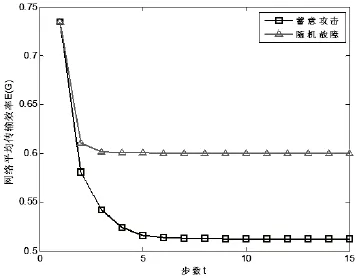
图2 随机攻击与蓄意攻击对比

2.2 网络初始效率研究

式（3）给出了连边初始传输效率的估计方法。本节将对参数θ的作用进行分析，研究其对整体网络初始效率以及相继故障破坏程度的影响。为了便于比较，文章将网络中连边的初始传输效率进行了归一化处理。假设网络中所有连边的初始传输效率之和固定，令其表示为ψ，则有：

式中，λij0为参数θ确定后得到的边传输效率，为边的归一化初始传播效率。

令网络中负载最大的前20个节点发生初始故障。仿真网络的节点数为1 000，转发容差α=0.2，缓存容差β=20，实验结果取10次以上平均值，结果如图3所示。

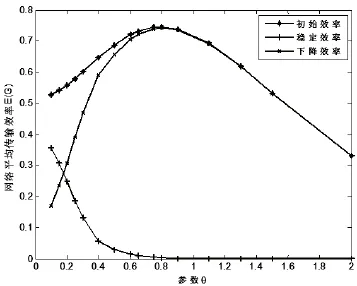
图3 θ值对网络的影响

图3中，在θ值较小时，随着其数值的增大，网络的平均传输效率E(G)不断增大，增长到最大值后形成一个拐点，之后网络的初始平均传输效率随θ的增大而减小。另外，在网络初始效率增大的过程中，网络在受到相同的蓄意攻击后，平均传输效率下降的幅度也随之增大。这是由于网络中各节间的初始负载分布随初始效率的增加而变得更加不均匀，从而导致网络对蓄意攻击的抵御能力逐渐减弱。而当网络的初始效率达到最大时，蓄意攻击引发的相继故障能够使整个网络完全崩溃。因此，设计通信网络链路间的初始效率时，应当令θ为符合网络传输需求的较小值，以同时满足网络的有效性和可靠性需求。

2.3 网络容差参数分析

为了对节点的特性进行描述，本文定义了转发容差α和缓存容差β。本节研究这两个重要参数对网络健壮性的影响。实验过程中，令参数θ=1。

首先，在节点缓存容差一致的情况下，研究转发容差的作用。在具有1 000个节点的网络中，通过令负载最大的前15个节点发生损坏而引起整个网络发生相继故障，实验结果取10次结果平均值，如图4所示。图4记录了发生相继故障后网络的平均传输效率随转发容差α的变化。其中，纵坐标表示网络在发生相继故障后重新稳定时的平均传输效率。

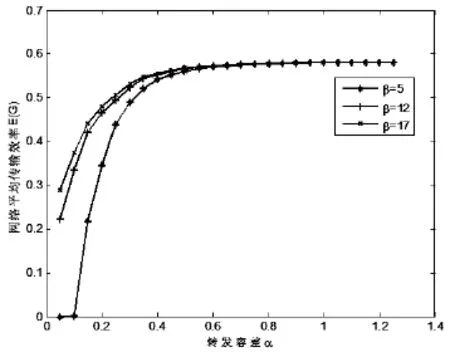
图4 转发容差对网络健壮性的影响

从图4中可以看出，随着节点转发容差的增加，网络稳定时的平均传输效率开始快速增长，直至趋于平稳。这说明当转发容差较小时，增加转发容差能够有效增强网络对相继故障的抵御能力。但是，当转发容差达到一个临界值后，增加转发容差就不再能够提升网络的健壮性。另外，针对三种不同的缓存容差进行了实验。结果表明：在转发容差较小时，提升节点的缓存容差也能提升网络的健壮性，但是随着转发容差的增加，缓存容差的作用逐渐减小，直至趋于零。

同样地，实验结果取10次结果平均值，则发生相继故障后网络的平均传输效率随缓存容差β的变化情况，如图5所示。由图5可知，大的缓存容差能够减小相继故障的影响。随着缓存容差的增长，网络稳定时的平均传输效率有一个明显的相变过程，可以用式（12）对该现象进行解释。从式（12）可以发现，阻塞概率pfull在bi相对较小时增长非常迅速，但是当bi变大时，增长就会逐渐放缓。这与图5记录的过程是一致的。在整体网络中，如果多数节点的缓存长度较小即缓存容差β较小，那么阻塞概率将对缓存的长度变化非常敏感。因此，改变缓存容差就会引起大量节点状态的改变，从而最终导致网络的平均传输效率呈现相变过程。

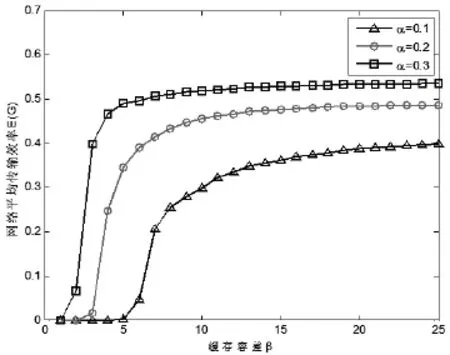
图5 缓存容差对网络健壮性的影响

3 结 语

本文重点考虑通信网络拥塞对网络性能的影响，并应用复杂网络理论建立了双限制相继故障模型。建模过程中，考虑通信网络的拓扑特性和功能特性，对网络节点同时施加转发能力和存储能力的限制，并通过仿真实验研究双限制模型中的关键参数对网络鲁棒性的影响，同时提出了一些合理构建通信网络的建议，以增强网络抵御相继故障的能力。随着通信技术的进一步发展，更多复杂的通信网络将会被设计和建设。因此，提高网络健壮性以抵御相继故障的危害，对于经济社会而言具有重要意义。

[1] Rahnamay-Naeini M,Hayat M M.On the Role of Powergrid and Communication System Interdependencies on Cascading Failures[C].Global Conference on Signal and Information Processing (GlobalSIP),2013IEEE,2013:527-530.

[2] Mukherjee B,Habib M,Dikbiyik F.Network Adaptability From Disaster Disruptions and Cascading Failures[J]. Communications Magazine,2014,52(05):230-238.

[3] Barabási A L,Albert R.Emergence of Scaling in Random Networks[J].Science,1999,286(5439):509-512.

[4] Crucitti P,Latora V,Marchiori M.Model for Cascading Failures in Complex Networks[J].Physical Review E,2004,69(04): 266-289.

[5] Motter A E,Lai Y C.Cascade-based Attacks on Complex Networks[J].Physical Review E,2002,66(02):114-129.

[6] Fu G,Dawson R,Khoury M,et al.Interdependent Networks:Vulnerability Analysis and Strategies to Limit Cascading Failure[J].The European Physical Journal B,2014,87(07):1-10.

[7] Gao J,Buldyrev S V,Stanley H E,et al.Networks Formed From Interdependent Networks[J].Nature physics,2012,8(01):40-48.

[8] Chen Z,Du W B,Cao X B,et al.Cascading Failure of Interdependent Networks With Different Coupling Preference Under Targeted Attack[J].Chaos,Solitons & Fractals,2015(80): 7-12.

[9] Kornbluth Y,Lowinger S,Cwilich G,et al.Cascading Failures in Networks With Proximate Dependent Nodes[J].Physical Review E,2014,89(03):032808.

[10] Asztalos A,Sreenivasan S,Szymanski B K,et al.Cascading Failures in Spatially-embedded Random Networks[J]. PloS one,2014,9(01):e84563.

[11] Brandes U.A Faster Algorithm for Betweenness centrality[J]. Journal of Mathematical Sociology,2001,25(02):163-177.

[12] 徐 恪,吴建平,徐明伟.高等计算机网络:体系结构,协议机制,算法设计与路由器技术[M].北京:机械工业出版社,2003. XU Ke,WU Jian-ping,XU Ming-wei.Advanced Computer Network Architecture Protocol Mechanism,Algorithm Design and Router Technology[M].Beijing:Machinery Industry Press,2003.

[13] 孟玉珂.排队论基础及应用[M].上海:同济大学出版社,1989. MENG Yu-ke.Queuing Theory and Its Application[M]. Shanghai:Tongji University Press,1989.

[14] Latora V,Marchiori M.Efficient Behavior of Small-world Networks[J].Physical Review Letters,2001,87(19):198701.

[15] Mizutaka S,Yakubo K.Structural Robustness of Scalefree Networks Against Overload Failures[J].Physical Review E,2013,88(01):2681-2694.

刘笑辰（1990—），男，硕士研究生，主要研究方向为通信网、复杂网络；

朱 磊（1973—），男，博士，教授，主要研究方向为网络管理、复杂网络、数据工程；

夏 苏（1990—），女，硕士研究生，主要研究方向为通信网、复杂网络。

A Research Of Modeling Cascading Failure For Communication Networks

LIU Xiao-chen，ZHU Lei,XIA Su
(Communication Engineering Institute, PLA University of Science and Technology, Nanjing Jiangsu 210007,China)

The topology of large-scale communication networks has characteristics of complex networks. However, as an inherent phenomenon, cascading failures has a serious threat on networks. In this paper, we propose a new cascading failure model for communication networks named double limit cascading model. By this model, we first research the relationship between the initial allocation of efficiency among edges and the robust of networks. The result shows that increasing network initial efficiency decreased the robust of networks within a certain range. We also research some important network parameters of communication network in cascading failures, especially forwarding data rate and cache size of routers. According to the result of experiments, we some recommendations to build a more robust communication network.

Cascading failure;Communication networks;Network robust;Router

TP393

：A

：1002-0802(2016)-06-0735-06

10.3969/j.issn.1002-0802.2016.06.016

2016-02-05;

：2016-05-07 Received date:2016-02-05;Revised date:2016-05-07

江苏省自然科学基金项目(No. BK20141071)

Foundation Item: Natural Science Foundation of Jiangsu Province (No. BK20141071)