一种基于双曲正割函数的变步长LMS算法*

王 蒙，赵建平，张炳婷

(曲阜师范大学 物理工程学院，山东 曲阜 273165)

一种基于双曲正割函数的变步长LMS算法*

王 蒙，赵建平，张炳婷

(曲阜师范大学 物理工程学院，山东 曲阜 273165)

在变步长自适应算法的基础上，结合双曲正割函数，建立了步长因子μ和误差信号e(n)之间一种新的非线性函数关系，从而提出一种新的变步长最小均方误差（LMS）算法，解决了固定步长算法收敛速度与稳态误差间的矛盾。详尽阐述新算法的基本原理，并对算法中关键参数的选取对滤波性能的影响进行分析，从而给出算法中关键参数的确定方法。通过在系统辨识的仿真实验证实，该算法拥有良好的性能。

LMS算法；双曲正割；收敛速度；稳态误差

0 引 言

自适应滤波器理论是信号处理领域的重要内容。因为自适应滤波算法是自适应滤波器设计过程中的重要环节,所以自适应滤波算法的研究是当今自适应信号处理中最为活跃的研究课题之一。最小均方误差（LMS）算法由Widrow和Holf于1960年提出，建立在维纳滤波理论的基础上，借助最速下降法通过迭代来逼近维纳解[1]。由于该算法具有计算量小、易于实现等优点，得到了广泛关注和大量应用。初始收敛速度、稳态误差、对时变系统跟踪能力以及抗噪声干扰能力，是评估LMS算法优劣的重要性能指标。在传统的LMS算法中，固定步长的取值不同会影响算法的性能：减少步长的取值可以得到较小的稳态误差，但同时会降低收敛速度和跟踪能力；而选取较大的步长虽然能够快速达到收敛，却有着较大的稳态误差。这就意味着传统LMS算法在收敛速度与稳态误差之间存在不可调和的矛盾[2]：无法同时拥有较快的收敛速度和较小的稳态误差。为此，人们提出了多种变步长LMS自适应滤波算法。

本文在文献[3]所提出的基于双曲正割函数的变步长LMS算法的基础上，进行数学变换和引入调节参数，建立起步长μ与误差的新的非线性函数关系，并提出新的变步长LMS算法。通过计算机仿真实验证实，该算法拥有理想的性能。

1 LMS算法的介绍

1.1 传统LMS算法

LMS算法是基于最小均方误差准则和最速下降法提出的，采用接收信号和期望信号之间的最小均方误差作为代价函数沿着代价函数梯度的负方向搜索，最终收敛于令代价函数最小的解。

自适应滤波器结构示意图如图1所示。

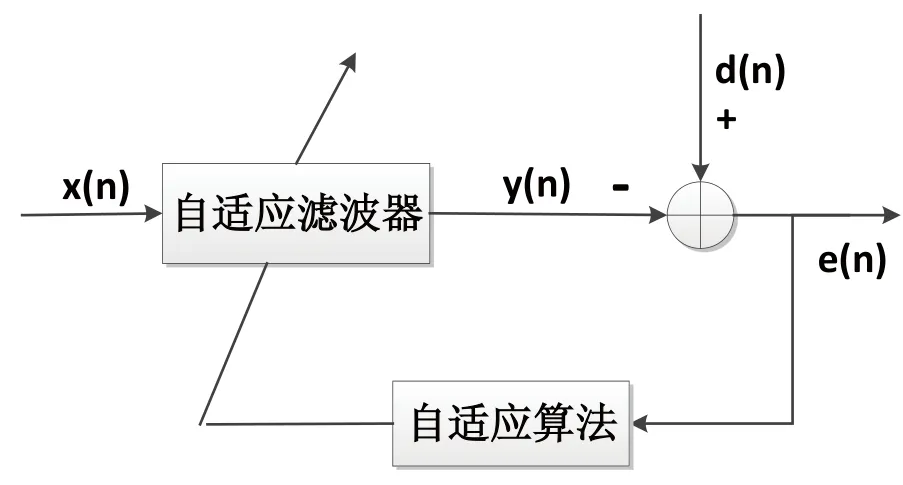
图1 自适应滤波算法结构示意

具体的自适应滤波算法流程如下：

根据文献[4]对传统LMS算法的理论分析，得出如下结论：

②在满足收敛的情况下，引入时间常数来衡量收敛速度。对于LMS算法来讲，在μ很小的情况下，LMS算法收敛速度是由最大的时间常数所决定。因为μ反比于时间常数，所以当μ越大时，时间常数越小，收敛速度越快。

这样在步长的选取上就存在一定的矛盾：在保证代价函数正常收敛的范围内，无法兼顾较快的收敛速度和较小的稳态误差。所以，人们提出了多种变步长算法。

1.2 已提出的几种常见变步长算法

文献[5]中，覃景繁等人根据sigmoid函数提出S函数算法，其步长更新函数为：

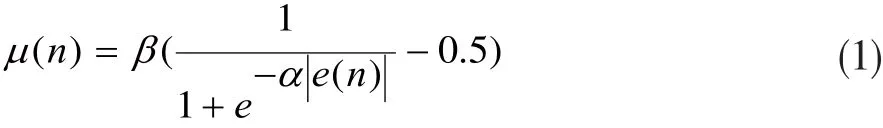
该算法很大程度上优于传统LMS算法，但是其在靠近0时变化较快，仍有较大的稳态误差。

文献[6]中，高鹰等人提出了G-SVSLMS算法，其步长更新公式为：

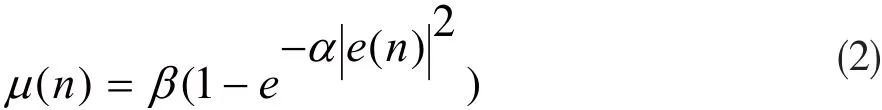
该算法克服了S函数LMS算法存在的问题，但是外界噪声对该算法具有很强的影响。在此基础上，有人提出了NG-SVSLMS算法[7]。NG-SVSLMS算法中，步长的更新公式变为：

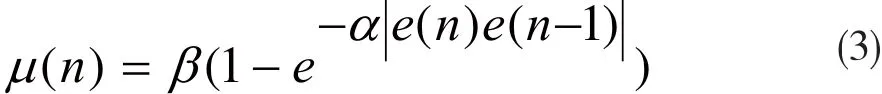
文献[3]中提出了基于双曲正割函数的变步长LMS算法，此处称其为sech-LMS算法，其步长更新公式如下：

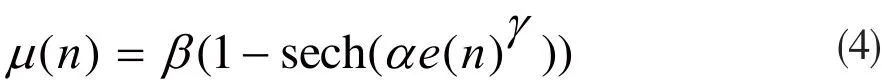
通过各文献所提出的变步长算法，总结出变步长LMS算法的基本原则：在初始收敛阶段时选取较大步长，以拥有较快的收敛速度；,在算法收敛后，选取较小的步长，且希望在误差接近0时尽量保持平稳，用以减小稳态误差。

2 一种新的变步长LMS算法

根据上文提到的变步长LMS算法的基本原则。本文提出了一种基于双曲正割函数的变步长LMS算法。

双曲正割函数的公式如式（5）所示，其图像如图2所示。

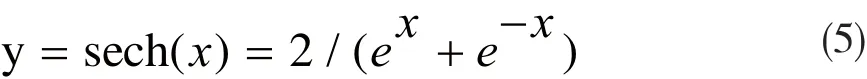
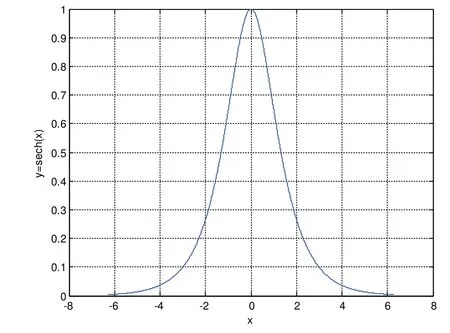
图2 双曲正割函数图像

根据双曲正割函数，可以得到本文即将用到的一个双曲正割函数。经过变化的函数公式如式（6）所示，其图像如图3所示。

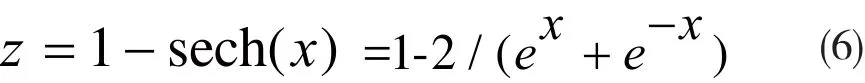
图3 经过变化后的函数的图像

从该函数的图形可以发现，它的变化规律符合步长因子的变化规律。因此，可以把用来描述z函数，则得到如下的推导公式：

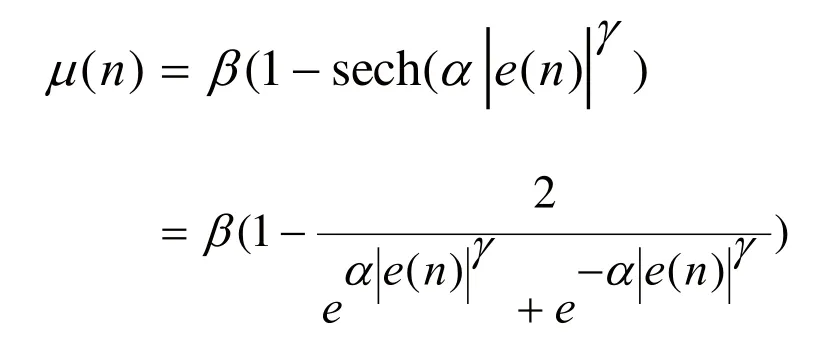
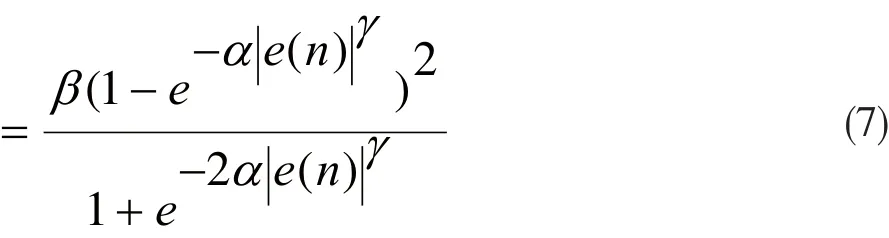
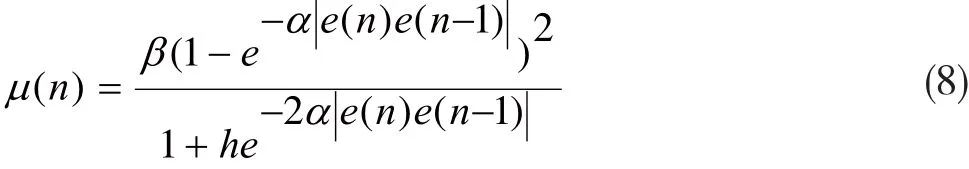
下面对步长因子中的参数进行分析。

①μ(n)为算法的步长，应满足收敛的条件，

②对于参数α，当固定β和h的取值时，α分别取1、2、3时的图像如图4所示。

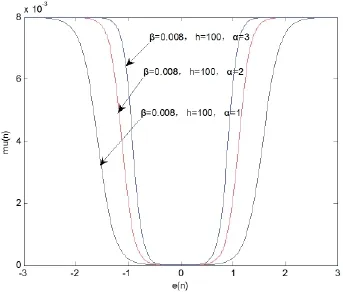
图4 仅α取不同值时的步长收敛情况

由图4得出结论：在同一误差情况下，α越大，步长越大，收敛速度较快，但是较大的α在靠近原点时，步长变化太快，会带来较大的稳态误差。

③针对α取值的矛盾现象，函数引入一个调节参数h，来调节底部的收敛状况，使步长在靠近0时不会有剧烈的变化而带来较大的稳态误差。

如图5所示，当其他参数固定，h的值从1到10再到100时，图像在靠近原点底部的变化越缓慢，所带来的稳态误差就越小。

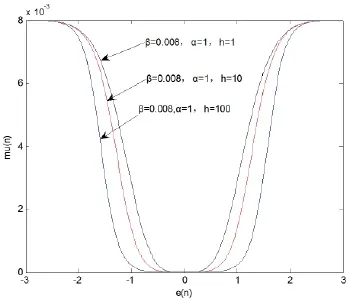
图5 仅h取不同值时步长的收敛曲线

3 算法在系统辨识系统中的应用分析

为了验证本文提出算法与其他算法相比的性能，现在系统辨识的应用中将本文提出算法同传统LMS算法、NG-SVSLMS算法、文献[3]提出算法进行比较。定义系统辨识的未知系统是8阶横向滤波器，抽头系数Hn=[0.878 5，-0.580 1，0.653 2，-0.322 4，0.657 1，-0.058 0，0.289 0，-0.271 5]。测量的输入信号与噪声信号的信噪比设置为20 dB。传统固定步长LMS算法β=0.002；sech-LMS算法取文献[3]中的β=0.008，α=3，γ=1；NG-SVSLMS算法中β=0.008，α=2；本文提出算法β=0.008，α=100，h=100。每种算法独立做200次仿真，然后对其求均值，得到的仿真结果如图6所示。

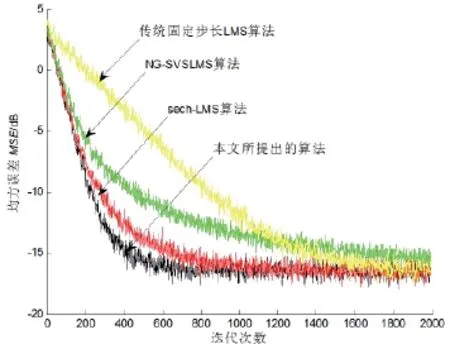
图6 四种算法收敛曲线比较

从图6可以清楚地看到，变步长算法相对于固定步长算法在收敛速度上有极大的提升。与其他类型变步长LMS算法相比，本文算法在稳态误差和收敛速度上有较大改进。本文提出的算法相对于文献[3]提出的sech-LMS算法，在稳态误差不增大的情况下，收敛速度上有较大提升。

4 结 语

根据变步长算法的步长因子调整原则，在原有基于双曲正割函数LMS算法的基础上，通过函数变形和引入调节参数，提出一种新的变步长LMS算法。通过理论分析和实验仿真，阐述了参数选取的方法，并将本文算法与其他算法一同应用在系统辨识中。经过实验仿真，证明本文所提出的算法确实能取得较快的收敛速度和较小稳态误差。但是，该算法在时变系统中的跟踪能力有待进一步的研究，以提出同时拥有较快收敛速度、较小稳态误差和较强跟踪能力的算法。

[1] Widrow B,Mccool J M,Arimoer M G. Stationary and NonStationary Learning Characteristics of the LMS Adaptive Filter [J]. Proceedings of the IEEE,1976, 64(08):1151-1162.

[2] 张炳婷,赵建平,马淑丽.新的变步长LMS算法在系统辨识中的应用[J].通信技术,2015,48(06):653-656. ZHANG Bing-ting,ZHAO JIAN-ping,MA Shuli. Application of Novel Variable Step Size LMS Algorithm in System Identification [J]. Communication Technology,2015,48(06):653-656.

[3] 吕春英,敖伟,张洪顺.一种新的变步长LMS算法[J].通信技术,2011,44(03):11-14. LV Chun-ying,AO Wei,ZHANG Hong-shun. A New Variable Step-Size LMS Algorithm [J]. Communication Technology,2011,44(03):11-14.

[4] 孟小猛.自适应滤波算法研究及应用[D].北京:北京邮电大学,2010. MENG Xiao-meng. The Research And Application Of Adaptive Filtering Algorithm [D].Beijing:Beijing University Of Posts And Telecommunications,2010.

[5] 覃景繁,欧阳景正.一种新的变步长LMS自适应滤波算法[J].数据采集与处理,1997,12(03):171-174. TAN Jing-fan,OUYANG Jing-zheng. A New Variable Step-Size LMS Adaptive Filtering Algorithm [J].Journal of Data Acquisition & Processing,1997, 12(03):171-174.

[6] 高鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报,2001,29(08):1094-1097. GAO Ying,XIE Sheng-Li. A Variable Step Size LMS Adaptive Filtering Algorithm and Its Analysis [J]. ACTC Electronica Sinica,2011,29(08): 1094-1097.

[7] 吕强,冯驰.一种变步长LMS算法及其Matlab仿真[J].应用科技,2006,33(06):80-82. LV Qiang,FENG Chi. A Variable Step Size LMS Algorithm and Its Matlab Simulation [J]. Apllied Science and Technology,2006,33(06):80-82.

王 蒙（1990—），男，硕士研究生，主要研究方向为无线通信技术；

赵建平（1964—），男，学士，教授，主要研究方向为无线通信技术；

张炳婷（1990—），女，硕士研究生，主要研究方向为无线通信技术。

A variable step size LMS algorithm based on hyperbolic secant function

WANG Meng,ZHAO Jian-ping,ZHANG Bing-ting
（College of Physics Engineering,Qufu Normal University,Qufu Shandong 273165,China）

On the basis of variable step size adaptive algorithm, combined with the hyperbolic secant function, it establishes a new nonlinear function relationship between the step size μ and the error signale(n), and then put forward a new variable step size minimum mean square error (LMS) algorithm, to solve the contradiction between the convergence speed and the steady-state error of the fixed step size algorithm .In this paper, the basic principle of the new algorithm is described in detail, and the key parameters of the algorithm are selected to analyze the impact of filtering performance, and give the method of determining the key parameters of the algorithm. By the experimental simulation in system identification, the algorithm has good performance.

LMS algorithm;Hyperbolic secant;Convergence speed;Steady-state error

TN911.7

：A

：1002-0802(2016)-06-0668-05

10.3969/j.issn.1002-0802.2016.06.004

2016-02-10;

：2016-05-06 Received date:2016-02-10;Revised date:2016-05-06

国家自然科学基金资助项目（No.11404185）；山东省高等学校科技计划项目资助（No.J12LN08）；曲阜师范大学技术开发项目（No.hxkj2015017）

Foundation Item: National Natural Science Foundation of China(No.11404185); Supported by the Science and Technology Project of Higher Education of Shandong Province(No.J12LN08); Qufu Normal University Technology Development Project（No.hxkj2015017）