最优画法的一个充分条件

王晶

(长沙学院 数学与计算机科学系,湖南 长沙，410022)

最优画法的一个充分条件

王晶

(长沙学院 数学与计算机科学系,湖南 长沙，410022)

设D是图G的一个好画法，将G在画法D下的交叉点看成新的顶点，这样得到的图称为G在画法D下的导出平图，记为GD。即GD的顶点集V(GD)=V(G)∪{交叉点}，边e由DV(GD)的片段组成，并且顶点v和边e关联的充分必要条件是v在边e的闭包里。本文证明了：如果画法D的导出平图的每个面的度数都是3，则D是最优画法。

交叉数；好画法；最优画法；导出平图

图的交叉数是图的一个重要参数，研究图的交叉数不仅具有重要理论意义,而且有较强的现实意义,如VLSI中的布线问题等。然而,一般地,确定图的交叉数又是十分困难的,Garey和Johnson在文献[1]中证明了确定图的交叉数问题是一个NP-完全问题。很多学者进行了这方面的研究，确定了完全图[2]、完全二部图[3]、 完全多部图[4,5]、笛卡尔积图[6-13]等一些重要图类的交叉数。与此同时，我们注意到，刻画最优画法性质方面的研究工作较少。众所周知，一个最优画法必定是好画法，但是反过来却不成立。自然地，我们会想，当一个好画法附加怎样的条件后，才能成为一个最优画法？在本文中，结合欧拉公式，我们得到了一个既简单又实用的结论。

本文未说明的概念和术语均同文献[14]；且无特别说明时，所涉及的图均指连通简单图。

1 几个定义

定义1 一个图G画在平面上,若满足如下条件:

(1)任何两条相交叉的边最多交叉一次；

(2)边不能自身相交；

(3)有相同端点的两条边不交叉；

(4)没有三条边交叉于同一个点；

则称此画法为G的一个好画法。

对于图G的任意一个好画法D，根据上述定义，显然有cr(G)≤crD(G)。

定义2 如果图G的某个好画法D满足crD(G)=cr(G)，则称D为图G的最优画法。

设D是图G的一个好画法，将G在画法D下的交叉点看成新的顶点，这样得到的图称为G在画法D下的导出平图，记为GD。即GD的顶点集V(GD)=V(G)∪{交叉点}，边e由DV(GD)的片段组成，并且顶点v和边e关联的充分必要条件是v在边e的闭包里。 从定义可以看出，GD是一个平图。

一个平图G把平面分成若干个连通区域，这些区域的闭包称为G的面，面f的度是指和f关联的边的条数。 更进一步的，令D是平图G的一个画法，若在画法D下，G的每个面的度都是3，则称D是图G的三角剖分。

2 主要结论

在本文中，利用欧拉公式，我们证明了如下结论：

定理1 设D是图G的一个好画法，如果D是导出平图GD的三角剖分，则D是图G的最优画法。

证明 分别用ν(G)和ε(G)表示图G的顶点数和边数，并且记导出平图GD的面的个数为φ(GD)。根据GD的定义，有

ν(GD)=v(G)+crD(G),ε(GD)=ε(G)+2crD(G)。

(1)

一方面，由于GD是平图，根据欧拉公式，有

φ(GD)=ε(GD)-ν(GD)+2，

(2)

同时，由于D是GD的三角剖分，可以得到

3φ(GD)=2ε(GD)，

(3)

联立(1)、(2)和(3)，可以得到

ε(G)-3ν(G)+6=crD(G)

(4)

对于图G，有cr(G)≥ε(G)-3ν(G)+6，结合式(4)，有cr(G)≥crD(G)。

另一方面，我们知道cr(G)≤crD(G)，所以cr(G)=crD(G)，即D是图G的最优画法。证毕。

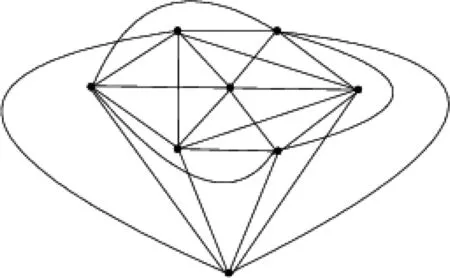
图1 图G′及它的一个好画法DFig.1 A graph G′ with its good drawing D

定理1给出了图G的好画法D为最优画法的充分条件,即要求其导出平图的每个面的度为3。很自然地,我们会问,这个条件能不能放宽? 例如,在画法D下,其导出平图中只有一个面的度不是3,其余面的度均为3,画法D是否还是最优画法? 答案是否定的! 我们举例来说明：

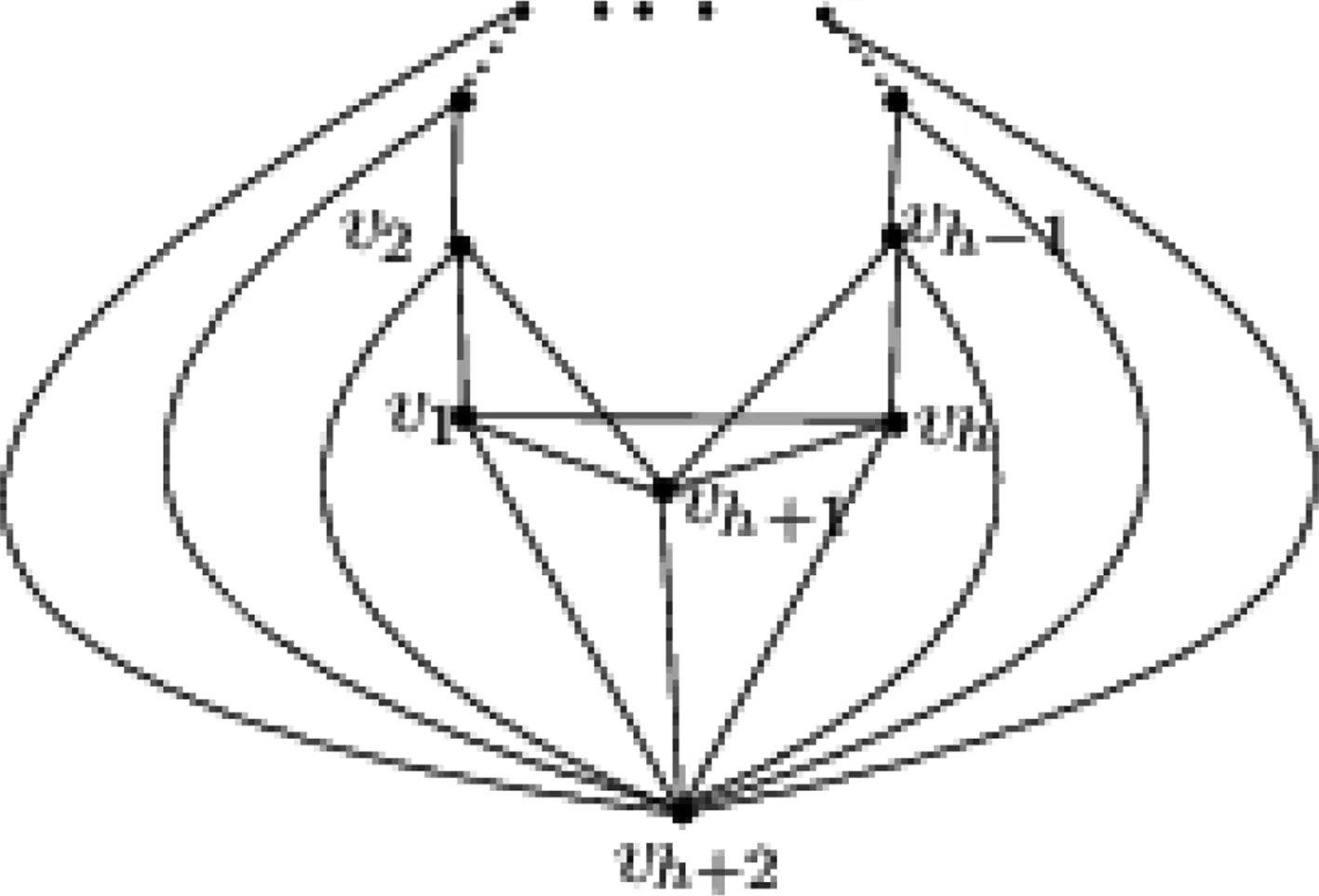
图2 图G″Fig.2 A graph G″

图2上图所示的是图G″及它的一个好画法D,可以看到在导出平图G″D中，有一个面的度为h(h≥4)，其余面的度都是3,且crD(G″)=2。图2下图所示的是图G″及它的另一个画法D′，而crD′(G″)=1。显然crD(G″)>crD′(G″)，即D不是图G″的最优画法!

尽管定理1中导出平图GD有关面的度的条件不能放宽,但是我们可以用类似于定理1中的方法，得到图G的交叉数cr(G)的下界。

定理2 设D是图G的一个好画法，如果其导出平图GD中一个面的度为h(h≥4)，其余面的度都是3,则有cr(G)≥crD(G)+3-h。

[1]Garey M R,Johnson D S.Crossing number is NP-complete[J].SIAM J.Algebraic Discrete Methods,1983,4:312-316.

[2]Shengjun Pan,R.Bruce Richter.The crossing number of K11is 100[J]. J.Graph Theory,2007,56:128-134.

[3]Kleitman D J.The crossing number of K5,n[J].J.Comb.Theory,1970,9:315-323.

[4]Asano K.The crossing number of K1,3,nand K2,3,n[J].J.Graph Theory,1980,10: 1-8.

[5]Yuanqiu Huang,Tinglei Zhao.The crossing number of K1,4,n[J]. Discrete Mathematics,2008,308:1634-1638.

[6]Beineke L W,Ringeisen R D.On the crossing numbers of products of cycles and graphs of order four[J]. J.Graph Theory,1980,4:145-155.

[7]Klesc M.The crossing number of K2,3×C3[J]. Discrete Mathematics,2002,251: 109-117.

[8]Peng Y H, Yiew Y C.The crossing number of P(3,1)×Pn[J].Discrete Mathematics,2006,306(16):1941-1946.

[9]Zihan Yuan,Ling Tang,Yuanqiu Huang,et al.The Crossing Number of C(8,2)□Pn[J].Graphs and Combinatorics,2008,24(06):597-604.

[10]Tang Ling,Lv Shengxiang,Huang Yuanqiu.The crossing number of Cartesian products of complete bipartite graphs K2,mwith paths Pn[J]. Graphs and Combinatorics,2007,23:659-666.

[11]Lv Shengxiang,Huang Yuanqiu.On the crossing number of K5×Sn[J].Journal of Mathematical Research & Exposition,2008,28(03):445-459.

[12]Zhangdong Ouyang,Jing Wang,Yuanqiu Huang.The crossing number of the Cartesian product of paths with complete graphs[J]. Discrete Mathematics,2014,328:71-78.

[13]周志东，李龙.一类联图的交叉数[J].邵阳学院学报(自然科学版)，2016，13(3)：16-24.

[14]Bondy J A.Murty U S R. Graph Theory with Applications [M],London：the macmillan press Ltd,1976.

A sufficient condition of optimal drawing

WANG Jing

(Department of Mathematic and Computer Science,Changsha College,Changsha 410022,China)

LetDbe a good drawing of the graphG,the induced plane graph ofD,denoted byGD,is the graph with verticesV(GD)=V(G)∪{crossings},where the edges are the components ofDV(GD) andvis incident toeif and only ifvis in the closure ofe.In this paper,we prove that if each face of the induced plane graphGDofDis triangle,thenDis optimal.

crossing number;good drawing;optimal drawing;induced plane graph.

1672-7010(2016)04-0022-04

2016-06-02

湖南省自然科学基金资助项目(14JJ3138)

王晶(1981-)，女，湖南邵阳人，副教授，博士，从事图论及其应用研究;E-mail:wangjing1001@hotmail.com

O157.5

A