弧形体挠性接管声阻抗特性研究
邓 杰 王洪磊
(海军驻四四九厂军事代表室 梧州 543004)
弧形体挠性接管声阻抗特性研究
邓 杰 王洪磊
(海军驻四四九厂军事代表室 梧州 543004)
弧形体挠性接管是一种新型高性能的挠性接管,具有优良的减振性能和较大的位移补偿能力,且可靠性高,在舰船上得到大量的应用.围绕弧形体挠性接管的结构特点,借助一维线性声波理论,推导了变截面管中的一维声波方程,并得到弧形体挠性接管在轴向方向的管内声阻抗矩阵,对其声阻抗特性进行了分析.
弧形体挠性接管;线性声波理论;声阻抗
0 引 言
管内流体的激励作用是引起管道振动及噪声的重要因素,也是声传播的重要载体.挠性接管作为机械设备与管道间的弹性连接件,不但需要在结构布置上应能够补偿一定的位移,自身应该具有隔离结构振动的作用,并且对管路内的流体扰动还应该能够起一定的衰减作用[1-3].挠性接管本身材料的粘弹性特性会吸收一部分声能量,对噪声有一定的衰减作用,但由于弧形体挠性接管弧形结构的特殊性,对内部流场会有一定的扰动,要明确弧形体挠性接管对内部流场的总体作用,有必要对其传声特性进行分析研究.由此,一方面是可以获取管路内部流体的运动规律,探明流噪声在管路中产生及传递的原理;另一个方面可以为挠性接管的优化设计提供指导帮助[4-6].
文中基于流体的质量连续方程、运动方程与物态方程,且考虑弧形体挠性接管结构的特殊性及管壁材料的粘弹性特性,根据平面线性波假设,采用频率法并结合阻抗的概念,用分布参数处理法,推导变截面管中声波的一维波动方程,计算了弧形体挠性接管挠性段的输入声阻抗、传递声阻抗及传递损失,并分析了各参数对声阻抗和传递损失的影响[7-8].
1 弧形管内声场基本方程的建立
管路是传播平面波的良好环境,声波在管路中仅沿轴向方向传播.可以通过理想介质的3个基本方程,消掉部分物理量获得某一参量表示的声波方程,来描述声波在管路中传播的规律.
输流管路内部声场的特征可以用声波来描述,声波是一个宏观的物理量,须满足牛顿第二定律、质量守恒定律和热力学定律.基于这3大定律能够建立管内流体介质的运动方程、连续性方程及物态方程.
弧形体挠性接管管体呈弧形结构,可以看作是一段弧线绕x轴旋转1周所得.其管内流通面积是逐渐变化的,且关于旋转轴对称,假定弧形管中传播的声波,其波阵面也是按照流通面积的变化规律而变化.取弧形管的纵剖面图进行分析,建立直角坐标系,见图1.把左端面的中心作为原点坐标,旋转轴为x坐标.

图1 弧形管结构简图
弧形管管壁的弧形半径为r,管长为L,管壁弧形中心与旋转轴的偏心距为d,管体沿x轴不同位置处的流通面半径为R,流通面的面积为S.由弧形管的几何结构特点可知,弧形管各个结构参数之间满足下面关系式.
(1)
取截面1及其相邻截面2之间的流体微团进行分析,管内流体静压力为p0,截面1与截面2之间的轴向距离为dx.假设在时间t时,截面1与坐标原点的距离为x,此时截面1处的流速为V,脉动压力为p,密度为ρ,管体的流通面积为S.可知V,p,ρ都是坐标x及时间t的函数,流通面积S仅是坐标x的函数.由此可得弧形体挠性接管中3大基本方程

(2)

(3)

(4)
式中:Kf为流体的体积弹性系数;R为管道流通面的半径;E为管壁材料的弹性模量;δ为管壁的壁厚;C是修正系数,不同情况下其取值不同,当挠性接管一端固定时有C=1-μ/2,两端都固定时有C=1-μ2,两端自由时有C=1,μ为泊松比.
结合连续方程、运动方程和物态方程,消去变量V,可得
(5)
式(5)即为弧形体挠性接管中的声波方程,该式也适用于其他的变截面管道.
2 声波方程的近似解
由式(5)可知,弧形体挠性接管中的声波方程是一个变系数的常微分方程,该方程除几个特定情况外很难获得其精确的解析解.
假定该方程有特定的指数解p=p(x)ejωt,代入到式(5)中,方程整理得
(6)
式中:k=ω/c是波数,ω是声波的圆频率;S′=dS/dx.
假设式(6)的解为变系数的指数函数,即
p(x)=B(x)ejγx
(7)
式中:B(x)和γ待定,γ是常数.
把式(7)代入式(6)中,整理得
(8)
要使式(8)恒成立,必须使其实部和虚部分别等于零,由此可得
由式(1)可知,R是x的函数,有S′/S=2R′/R,R′=∂R/∂x,代入式(9)的第二个式子中,积分可以得到
B(x)=1/R
(10)
把式(10)代入式(9)的第一个式子中可解得
(11)
式中:R″=∂2R/∂x2.
要满足γ是常数的条件,必须有R″/R=C,C是常数,由式(1)可知,R不满足该条件.为此弧形管的声波方程不能通过该方法得到精确的解析解.
当管道截面呈线性变化时,显然可以满足R″/R=C的条件,为此把弧形管简化成n段等长的锥形管连接而成的管道,每段锥形管长度为ΔL=L/n,见图2.当弧形管分的段数足够多时,可以保证计算的精度.

图2 弧形管简化模型
取第i段管进行分析,令其左端面和右端面的轴向坐标分别为xi-1和xi,其半径Ri(x)为
Ri(x)=mi(x-xi-1)+R(xi-1)
(12)
式中:mi为第i段锥形管管壁的斜率,mi=[R(xi)-R(xi-1)]/ΔL,x⊆(xi-1,xi).
此时有:
R″i(x)/Ri(x)=0
Bi(x)=1/Ri(x)=1/[mi(x-xi-1)+R(xi-1)]
γ=k=ω/c
(13)
将式(10),(12)和式(13)代入式(7)中,可得第i段锥形管中声压的一般表达式
(14)
这就是第i段锥形管中声波方程的解,式子中的前一项表示沿x正向传播的前进波,后一项表示沿x反向传播的反射波.C1和C2是2个常系数,通过边界条件来确定.
根据运动方程式(3),可知
(15)
这就是第i段锥形管流体的流速.
3 弧形管声传递矩阵与声阻抗矩阵的建立
弧形管是典型的两端元件,将其看作是一个声学单元,根据平面波假设,其端面的声学状态可以用声压p及质点体积流速Q2个状态参数来描述,容易知道Q=SV.每一个声学单元可以看作是一个四端网络,该四端网络反映了弧形管的传递特性,即传递矩阵.
同样,每一段锥形管也看作是一个声学单元,它的四端网络见图3.假设第i段锥形管左端面即x=xi-1时的状态参数为pi-1和Qi-1,右端面即x=xi时的状态参数为pi和Qi,四端网络可以用式(16)表示,此即是第i段锥形管两端面间的传递矩阵,将n段首尾相连的锥形管的传递矩阵连乘,就能够求得弧形管的传递矩阵.
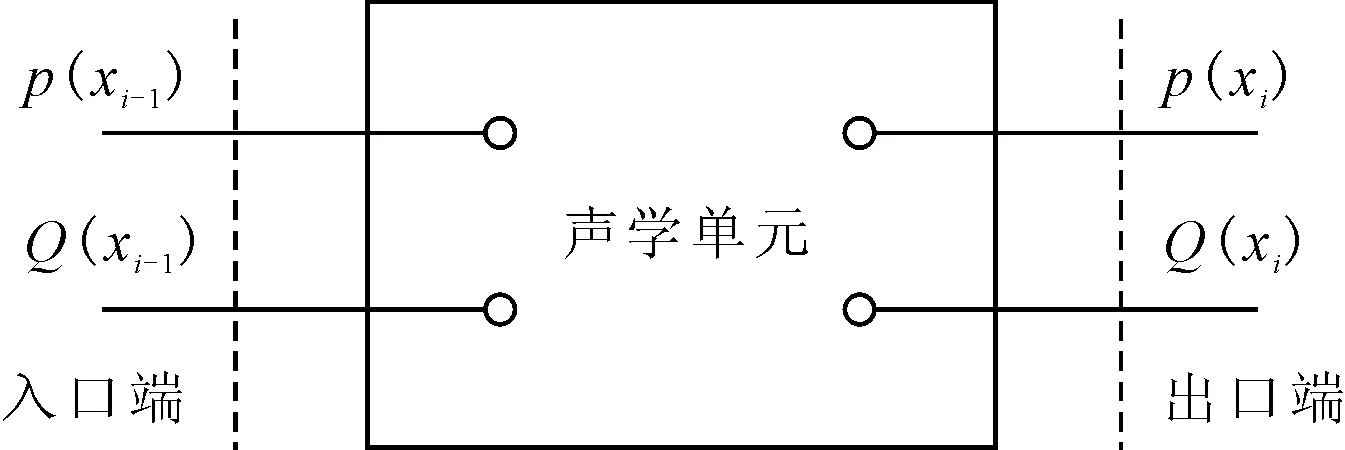
图3 声学单元四端网络
(16)
式中:Ti为第i段管传递矩阵;T11i,T12i,T21i,T22i为四端网络参数.
将边界条件代入声波方程的解,即式(14)和式(15)中,可求出式(16)中传递矩阵Ti的各元素如下.
(17)
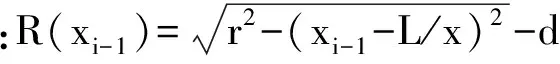
根据式(17),可以求得总体管中每一段锥形管的传递矩阵Ti,将首尾相连的锥形管的传递矩阵连乘可求得弧形管的传递矩阵T,即
(18)
利用传递矩阵与阻抗矩阵的关系,能够得到弧形管的声阻抗矩阵为
(19)
4 实例计算
前面推导了弧形体挠性接管内部流场声传播的传递矩阵和声阻抗矩阵,下面选用DN80型弧形体挠性接管为例进行计算分析.管内流体是水,其体积弹性系数为Kf=2.06×109Pa,密度为1 000 kg/m3,管内声波的传播速度为274.1 m/s.解得结果以幅频图的形式表示,并将结果与等直管的相应声阻抗曲线进行比较,见图4~6.图中Za11为输入声阻抗;Za21为传递声阻抗;TL为传递损失;AP为弧形管;SP为等直管.
由图4~5可知,r=72 mm时,弧形管的声阻抗曲线与等直管的声阻抗曲线有相同的变化趋势,弧形管的第1阶共振频率要比等直管的第1阶共振频率低23 Hz,第1阶反共振频率比等直管的第1阶反共振频率大201 Hz.弧形管的阻抗幅值比等直管的要小5.4 dB左右.在较高频区,弧形管和等直管2者声阻抗曲线吻合度较好,由此可知弧形管的弧形结构主要影响低频区声阻抗,对中高频段区域的声阻抗影响较小.

图4 r=72 mm时的声阻抗

图5 r=300 mm时的声阻抗

图6 r=1 000 mm时的声阻抗
由弧形管的结构可知,当其他参数不变,弧形管的母线半径变大时,其弧度越趋于平缓,半径无限大时,弧形管就近似于一等直管.由图4~6可知,随着弧形管母线半径的变大,弧形管的声阻抗曲线逐渐趋近于等直管的声阻抗曲线,当弧形管的母线半径达到1 000 mm时,弧形管的声阻抗曲线和等直管的声阻抗曲线几乎完全重合.这说明弧形管声传递矩阵的推导是合理可行的.
5 结 束 语
根据平面波假设,推导了弧形管中的一维声波方程,该方程亦适用于其他的变截面管道.将弧形管简化成n段锥形管首尾相连而成,推导了弧形管内部声场的传递矩阵与声阻抗矩阵,并对DN80型弧形体挠性接管的声阻抗进行了计算,可以看出弧形管对流噪声有一定的衰减作用,与直管进行比较,分析了弧形管弧形半径对声阻抗的影响,可知弧形管的声阻抗比等直管的要小,随着弧形半径的增大,声阻抗增大,其阻抗曲线逐渐趋近于等直管的阻抗曲线.
[1]刘忠族,孙玉东,周庆云.管路柔性元件声阻抗测试方法研究[J].舰船科学技术,2006,28(增刊2):125-127.
[2]柴小文.舰船用挠性接管技术现状和进展[J].噪声与振动控制,2007(5):13-16.
[3]堵锋,孙玉东,钟荣.锥管中流动工作介质的声传递特性研究[J].船舶力学,2011,15(7):55-58.
[4]杜功焕,朱哲民,龚秀芬.声学基础[M].南京:南京大学出版社,2012.
[5]徐合力.船舶输流管系振动特性研究[D].武汉:华中科技大学,2008.
[6]戴安东,陈刚,朱石坚.舰船管路振动噪声控制措施综述[J].船海工程,2001,30(2):75-78.
[7]邓杰,周炜,帅长庚.弧形结构旋转薄壳机械阻抗计算方法研究[J].海军工程大学学报,2015,27(6):47-50.
[8]李艳华,柳贡民.流体管道流固耦合14方程频域传递矩阵法[J].船海工程,2009,38(5):106-111.
Investigation on the Acoustic Impedance Characteristics of Arc-type Flexible Pipe
DENG Jie WANG Honglei
(NavalDeputyOfficeof449Shipyard,Wuzhou543004,China)
Arc flexible pipe belongs to a new and high-performance type of flexible pipe which is effective in reducing vibration and compensation for displacement. Besides, it is highly reliable. It has been widely applied on ships and warships. This paper aims at studying the mechanics characteristics of the Arc flexible pipe, based on the one-dimensional linear sound wave theory. The acoustic wave equation in variable cross-section pipes is deduced. The axial acoustic impedance of the Arc flexible pipe is computed. This paper also analyzes the acoustic impedance characteristics.
arc flexible pipe; linear sound wave theory; acoustic impedance
2016-10-26
U664.84
10.3963/j.issn.2095-3844.2016.06.035
邓杰(1990—):男,工学硕士,助理工程师,主要研究领域为舰船建造、检验

