应用ANSYS用户可编程特性实现梁单元开发研究*

黄 斌 邓洪洲

(同济大学建筑工程系 上海 200092)

应用ANSYS用户可编程特性实现梁单元开发研究*

黄 斌 邓洪洲

(同济大学建筑工程系 上海 200092)

应用ANSYS平台提供的UPFs二次开发工具，对考虑几何非线性梁元的开发过程进行探索.对于用到的子程序文件uec102，uel102，以及uep102进行了研究，编写代码实现了梁单元开发，并通过经典算例校验了程序的可靠性.同时，在一般梁元开发研究基础上，进一步创建了能够考虑节点刚度影响的新型梁元，应用于一单层球面网壳结构中，与普通梁元加弹簧模拟方法进行了比较，两者计算结果吻合较好，证明了该方法的可行性.

ANSYS二次开发；几何非线性；梁单元开发；节点刚度

0 引 言

对于网壳结构中构件通常按照两端铰接的轴心受力模型进行验算.但实际结构节点并不完全铰接，存在一定的抗弯刚度.在用ANSYS软件进行有限元分析时，对于考虑节点刚度影响的构件常使用梁单元加弹簧方式进行模拟，但就目前ANSYS单元库中的弹簧元而言，采用梁元两端连接弹簧，每个节点至少要连接2个弹簧，其中1个用于控制平动位移，另1个用于控制转角位移，如此，在进行建模时，每个节点要额外增加2个节点用于构建弹簧元，这样节点数量较多，且出现节点位置重合，增加建模难度.

文中应用ANSYS平台提供的用户可编程特性UPFs(user programmable features)从一般梁元创建出发，探索梁元开发过程.对于考虑节点影响构件，可将构件与半刚性节点作为一体，研究其等效单元刚度矩阵，作为一新型梁元单元刚度矩阵，在建模时不用再增加节点模拟弹簧元，仍可按梁元看待，降低了建模难度，提高了建模效率.

UPFs是对ANSYS程序提供的可供用户修改子程序文件(uex100～uex105)进行调整或修改，用于建立新型材料的本构关系，定义复合材料的失效准则，或根据用户要求开发具有特定力学性能的单元等[1].

1 梁单元的开发过程探索

1.1 单元形函数

文中一般梁单元为3节点线型单元，其中仅节点i，j对单元刚度有贡献，k节点为辅助节点，用于截面朝向的控制.

梁元形函数采用2节点(除去辅助节点k)3次hermite插值函数，单元场函数在节点处具有一阶导数连续性，为C1型单元，形函数如下所示[2].

采用量纲一的量坐标

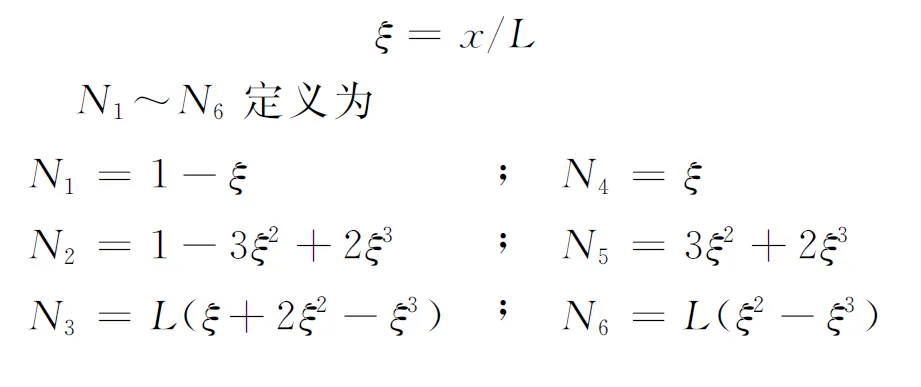
1.2 几何非线性分析

1.2.1 空间大转动处理

文献[3-5]给出了考虑几何非线性时空间大转动的处理方法.三维空间旋转变换除了指定旋转角外，还需指定旋转轴.

给定具有单位长度的旋转轴A=(ax,ay,az)和旋转角θ，则绕OA轴旋转变换的旋转矩阵Tθ表示为

(1)

式中：ax，ay,az为旋转轴的方向余弦.

1.2.2 单元坐标转换矩阵

坐标转换矩阵取决于单元坐标系与整体坐标系之间的相对位置关系.考虑几何非线性时，单元两端截面的位置不断变化见图1，因此需要更新每次迭代的坐标转换矩阵.

图1 单元坐标系示意图

梁单元坐标系与整体坐标系的转换矩阵为

式中：r为单元定向矩阵，可表示为

(2)

式中:rij(i，j=1,2,3)为单元局部坐标轴j(j=x,y,z)与整体坐标轴i(i=X,Y,Z)的夹角的方向余弦，r的第一列为单元局部坐标x轴与整体坐标系中各坐标轴的方向余弦，由现时构形下单元两端节点的位置即可得到，此时单元的长度为

单元矩阵的y轴与z轴在整体坐标系中相对位置的确定比较复杂.设节点坐标系的任意时刻的坐标矩阵为

式中：α为节点坐标系的坐标轴任意时刻与整体坐标轴夹角的方向余弦矩阵.

初始构形下节点坐标系分别平行于3根整体坐标系的坐标轴，则初始节点坐标系矩阵为

假设在t时刻αt已经求得t+Δt时刻的转角增量为Δθ(Δθx，Δθy，Δθz)，则根据式(1)可以得到t+Δt时刻的节点定向矩阵αt+Δt.

αt+Δt=TΔθαt

(3)

式中：αt+Δt为节点坐标系相对于整体坐标系的位置.定义端截面定向矩阵S.S的第一列为截面法线的方向余弦，其余两列为截面主轴的方向余弦.则有

Sit+Δt=αit+Δtr0

Sjt+Δt=αjt+Δtr0

(4)

式中：r0为初始单元坐标的定向矩阵.初始时刻，截面坐标系平行于单元坐标系，也即为截面坐标系的矩阵，r0的确定可参阅文献[6].

截面坐标系S确定之后，在上文单元坐标系的x轴的方向已经确定，因此，便可获得单元坐标系的x轴与截面坐标系的x轴之间的夹角，假定单元的相对变形是微小的，如下式.

(5)

为求r的第二、三列，令：

由此可根据两端截面的定向矩阵得到两单元坐标系的定向矩阵

Pit+Δt=Sit+Δteit+Δt

Pjt+Δt=Sjt+Δtejt+Δt

(6)

取单元截面主轴方向为两端截面主轴方向的平均值，则可得

(7)

1.3 UPFs子程序文件说明

主要用到的子程序文件有：uec102， uel102，uep102.

uec102文件用于描述所创建单元的基本特征，该子程序文件中主要是对一维数组ielc()进行赋值.uel102子程序文件是单元计算的核心程序.在该文件中单元刚度矩阵计算，内力计算，单元坐标转换矩阵的更新，非线性计算时Newton-Raphson恢复力的计算，非线性分析迭代的逻辑都需要在uel102中编写相应代码.uep102主要是用于控制线单元输出结果，用户可在此子程序中指定输出内容，如单元杆端力，单元应力等.

2 经典算例检验

为检验程序的可靠性及有效性，与经典算例进行了对比分析.

2.1 William平面刚架几何非线性分析

William平面刚架是结构几何非线性分析中的经典算例，其结构布置简图见图2.文中对2种不同高度(h=9.804，8.128 mm)的框架进行了计算分析.

图2 William框架结构简图(尺寸单位：mm)

图3～4分别对应h=9.804 mm时点A处荷载P-竖向位移δA曲线及荷载P-水平支座反力H曲线.

图3 点A处P-δA曲线

图4 P-H曲线

图5～6分别对应h=8.128 mm时点A处荷载p-竖向位移δA曲线及荷载p-水平支座反力H曲线.单元划分数量均为4单元.

图5 点A处P-δA曲线

图6 P-H曲线

2.2 六角星形穹顶平衡路径追踪

六角星形穹顶结构平衡路径分析也是几何非线性分析的经典算例，结构布置见图7.

图7 六角形猩猩穹顶结构布置简图(尺寸单位：cm)

文中在进行分析时，考虑到文中使用的形函数与ANSYS单元库中BEAM4的形函数相同，因此与使用了ANSYS的BEAM4梁元模拟的结果进行了对比.计算结果见图9～12.

图8～9为结构点1处的荷载位移曲线.图8单元划分数量均为1，图9单元划分数量为4.图10为4单元时，荷载与点2处的x向水平位移ux关系曲线，图11为4单元时点2处的z向位移uz关系曲线.

图8 点1处P-δ1曲线

图9 点1处P-δ1曲线

图10 点2处P-ux曲线

图11 点2处P-uz曲线

通过比较可知：2种方法的计算所得的荷载位移曲线基本重合，说明文中使用UPFs编写的程序在逻辑上是合理的.

2.3 六边形12构件空间框架几何非线性分析

文中选取了文献[7]中的六边形框架(见图12)算例进行了计算分析.，并与ANSYS单元库中的BEAM4单元进行对比.

图12 六边形空间框架(尺寸单位：mm)

计算结果见图13～14，图13为单元划分数量均为1单元，图14为单元划分数量均为4单元.两者的荷载位移曲线均较好的吻合.

图13 点A处P-δA曲线

图14 点A处P-δA曲线

3 新型梁元的网壳分析应用

对于网壳结构，许多学者为了考虑节点对结构计算结果的影响，提出了多种计算模型.在一般梁元开发研究的基础上，文中基于刚臂-弹簧模型，研究了考虑节点尺寸以及节点半刚性影响的构件等效刚度矩阵，并作为应用ANSYS的UPFs开发的新型梁元单元刚度矩阵，应用于一单层球面网壳结构计算分析中.

当不考虑节点尺寸的影响，仅考虑节点半刚性时，计算简图见图15.

图15 考虑节点半刚性单元计算简图

弹簧的力矩-转角关系可以表示为

Ms=Ksθs

(8)

Ms=[MyaMzaMyaiMzaiMyb

MzbMybiMzbi]T

(9)

θs=[θyaθzaθyaiθzaiθybθzbθybiθzbi]T

(10)

式中：θyai，θzai，θybi，θzbi为增加的内部节点自由度；Myai，Mzai，Mybi，Mzbi为与其对应的力矩.

式中：Rki为弹簧的转动刚度，与圆管相连的焊接球的转动刚度可根据文献[8-9]提供的公式计算.

构件采用普通梁元模拟每个单元有12个自由度，考虑弹簧之后，增加了4个内部自由度，此时，构件的自由度变为16个.将原构件的12×12刚度矩阵与弹簧的8×8刚度矩阵均扩展为16×16阶矩阵，并且进行合并，则有：

fa=Kaua

(12)

式中：

fa=[FxaFyaFzaMxaMyaMza

FxbFybFzbMxbMybMzb

MyaiMzaiMybiMzbi]T

(13)

ua=[uavawaθxaθyaθzaubvbwb

θxbθybθzbθyaiθzaiθybiθzbi]T

(14)

式(12)可写为

(15)

通过凝聚内部自由度，将U4消掉，由式(15)可得

(16)

将式(16)代入式(15)可得

(17)

式(17)中

(18)

(19)

(20)

进一步再考虑焊接球节点的尺寸影响，采用刚臂弹簧梁元模型，计算见图16.

图16 刚臂弹簧模型的计算简图

根据向量运算法则，a点的位移向量和荷载向量与A点的位移向量和荷载向量有如下关系

(21)

(22)

(23)

(24)

(25)

Kab与KAB之间的关系为

(26)

式(26)中，转换矩阵的表达式为

(27)

考虑焊接球尺寸影响时，可取exA为焊接球的半径长度，eyA=0，ezA=0.

文献[8]采用梁元连接弹簧元再加刚臂模拟网壳中的构件，考虑焊接球影响，对一单层球面网壳结构进行了分析计算.网壳结构布置图见图17～18.结构跨度30 m，矢跨比为1/4，杆件外径为0.077 5 m、内径为0.069 5 m，焊接球的直径为0.45 m、厚度为0.014 m.

图17 单层球面网壳结构布置图

图18 单层球面网壳1/8结构

文中将基于刚臂弹簧模型的等效刚度矩阵，作为一新型梁元的单元刚度矩阵，应用在单层球面网壳结构分析中，并分别计算对比了文献[8]中的2种工况下构件应力.工况1为网壳各节点均受竖向力10 kN，工况2为仅网壳的顶点受竖向力10 kN.

计算结果见表1～2，表中的“组合模型”是指文献[8]中构件采用梁元加弹簧元再加刚臂方法建立的模型，由表1～2可知，2种模型计算结果的轴应力比较接近，说明使用新型梁元模拟考虑节点刚度的构件的力学模型是可行的.

表1 工况1时的构件应力对比 ×108 N/m2

表2 工况2下的构件应力对比 ×108 N/m2

4 结 论

1) 在创建单元时，用到了3个子程序文件，分别为：uec102，uel102，uep102.uec102用于描述单元的基本特征，主要是给ielc数组赋值；uel102用于编写单元计算的核心程序；uep102主要用于线单元在后处理中的打印输出，需要输出的结果必须已经写入了结果文件中.

2) 通过经典算例检验了文中使用UPFs二次开发工具进行梁元开发所编写程序的可靠性，同时说明文中在开发过程中关键步骤处理的合理性.

3) 在网壳结构中常采用弹簧与梁元组合模拟网壳结构中的构件，此法建模复杂，文中应用UPFs创建了能够考虑节点刚度影响的梁元，并与弹簧梁元模型计算进行了对比，结果吻合较好，说明了该方法的可行性，因此，也能为其它多构件结构，考虑节点影响提供参考.

[1]师访.ANSYS二次开发及应用实例详解[M].北京:中国水利水电出版社,2011.

[2]陈正清,杨孟刚.梁杆索结构几何非线性有限元[M].北京：人民交通出版社，2013.

[3]ORAN C. Tangent stiffness in space frames[J]. Journal of the Structural Engineering,1973,99(ST6):987-1001.

[4]沈祖炎,罗永峰.网壳结构分析中节点大位移迭加跟踪技术的修正[J].空间结构，1994(1):11-16.

[5]沈祖炎,罗永峰.节点大位移条件下的梁-柱单元坐标转换矩阵[J].上海力学,1994,15(4):13-18.

[6]罗永峰.网壳结构弹塑性稳定及承载全过程研究[D].上海：同济大学，1991.

[7]王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007.

[8]刘海峰,罗尧治,许贤.焊接球节点刚度对网壳结构有限元分析精度的影响[J].工程力学，2013,30(1):350-358.

[9]王星，董石麟，完海鹰.焊接球节点刚度的有限元分析[J].浙江大学学报,2003,34(1)：77-82.

Study on the Development of Beam Element Applying the ANSYS User Programmable Features

HUANG Bin DENG Hongzhou

(DepartmentofStructuralEngineering,TongjiUniversity,Shanghai200092,China)

The User Programmable Features (UPFs) secondary development tools provided by ANSYS platform is to explore the process of establishing the beam element considering the geometric non-linearity. Sub program files uec102, uel102 and uep102 are studied which are used in the process of establishing the beam element, and the reliability of the program are checked through the classic example. A new type of beam element is developed considering the effect of joint stiffness to improve the efficiency of modeling and the whole calculation process. Besides, this new beam element is applied to a single layer spherical reticulated shell structure. Compared with the calculating method based on the common beam element and spring element, the results show good agreement, which proves the feasibility of the method based on the new type of beam element developed using UPFs.

secondary development of ANSYS; geometric nonlinearity; beam element development; joint stiffness

2016-09-07

*国家电网公司科技项目(521300130CSS)、国家自然科学基金项目(51578421)资助

TU3

10.3963/j.issn.2095-3844.2016.06.010

黄斌(1985—)：男，博士生，主要研究领域为输电铁塔节点极限承载力