一类推广的共轭梯度法及收敛性分析

郑小平，陈忠 (长江大学信息与数学学院，湖北 荆州 434023)



一类推广的共轭梯度法及收敛性分析

郑小平，陈忠 (长江大学信息与数学学院，湖北 荆州 434023)

共轭梯度法由于其计算量小、收敛速度快，在求解大规模无约束问题中起着重要作用。通过对参数βk的修正，构造了一种求解无约束问题新的共轭梯度算法，并证明了算法的全局收敛性。

无约束最优化；共轭梯度法；充分下降性；线搜索；全局收敛性

考虑无约束最优化问题：

(1)

其中，f:Rn→R为连续可微函数。求解问题(1)的迭代公式为：

xk+1=xk+αkdk

(2)

(3)

式中，gk=f(xk)；dk为搜索方向；αk≥0为步长因子；选取不同的βk可以构成不同的共轭梯度算法。比较常见的βk选取公式[1～4]有：

其中,‖·‖为欧式范数。

文献[5]给出了一族包含CD方法的新共轭梯度算法,并证明了它们在非精确线性搜索下具有全局收敛性；文献[6]给出了收敛共轭梯度法参数βk的构造条件并建立了其收敛性定理。下面笔者给出一种新的βk的选取方法：

(4)

式中，μ为参数。

显然, μ=0时式(4)为CD公式，μ=1时式(4)为HS公式。

1 算法描述

步1 给定x1∈Rn，ε>0，0<ρ<σ<1，令d1=-g1，k=1；

步2 利用Wolfe线性搜索准则求得αk：

(5)

(6)

步3 计算xk+1=xk+αkdk；如果‖gk+1‖≤ε，则停止；否则转步4;

步4 由式(4)计算βk，由式(3)计算dk；

步5 令k=k+1，转步2。

2 算法全局收敛性

假设(H)：

(ii)f(x)在水平集L的某个邻域N内，其导函数g满足Lipschitz条件，即存在常数M>0，使得:

‖g(x)-g(y)‖≤M‖x-y‖ ∀x,y∈N

(7)

证明采用数学归纳法。

当n=k-1时，由式(3)和式(4)有：

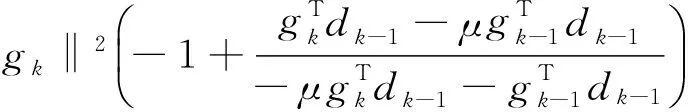
(8)

结合式(4)和式(6)可知：

综上，引理1得证。

(9)

证明采用反证法。假设定理1不成立，则存在常数c>0，使得：

‖gk‖2>c k=1,2,3,…

(10)

由式(6)可得：

从而有：

(11)

由式(3)可得：

dk+gk=βkdk-1

两边取平方移项可得：

故而有：

又：

则：

即：

[1]Hestenes M R, Stiefel E. Methods of conjugate gradients for solving linear syste-ms[J]. J Res Nat Bur Standards Sect,1952,49(5):409～436.

[2]Polyack B T. The conjugate gradient method in extreme problems[J].USSR Computational Mathematics and Mathematical Physics,1969,9(1):94～112.

[3]Fletcher R, Reeves C M. Function minimization by conjugate gradients [J]. The C-Omputer Journal, 1964,7(2):149～154.

[4]Fletcher R.Practical Methods of Optimization: Vol.2: Constrained Optimization [M]. John Wiley & Sons Inc,1987.

[5]高丽，谢铁军.Wolfe线搜索下新的共轭梯度法的全局收敛性[J].运筹与管理，2008，17(1):38～41.

[6]Zhang Liwei.Conditions on Parameter βkin a Convergent Conjugate Gradi-ent Method[J].运筹学学报，1999,3(2):71～81.

[编辑] 张涛

2016-09-15

国家自然科学基金项目(61273179)。

陈忠(1964-)，男，博士(后)，教授，博士生导师，现主要从事最优化理论与算法方面的教学与研究工作；E-mail：czhong@yangtzeu.edu.cn。

O224

A

1673-1409(2016)34-0001-03

[引著格式]郑小平，陈忠.一类推广的共轭梯度法及收敛性分析[J].长江大学学报(自科版)，2016,13(34)：1～3.