轧辊维修策略与备件库存联合优化研究
高 坤,张晓红,曾建潮
(太原科技大学,太原 030024)
轧辊维修策略与备件库存联合优化研究
高 坤,张晓红,曾建潮
(太原科技大学,太原 030024)
辊是使轧材产生塑性形变的主要工具,也是轧钢过程中的主要消耗部件,其合理的更换策略和库存设置对保证企业安全生产和降低生产成本至关重要。将同一生产线上多个轧辊组成的系统建模为一个同类可修多部件系统,结合轧辊本身的运行和维修特点,提出了成批更换及离线视情修磨相结合的轧辊更换修磨策略与 备件库存订购策略的联合策略,在考虑确定的修磨时间,交付时间和非完美修磨效果的基础上,分析了生产过程中轧辊的成批更换、视情修磨和备件订购的相互制约关系,建立了以更换周期、报废阈值和库存参数为决策变量,以单位轧辊无限时间范围内的平均费用率最小为目标的仿真优化模型,最后采用离散事件仿真和遗传优化算法相结合的方法对模型进行求解。仿真结果表明,联合优化所得到的更换周期和库存参数更合理的,可以有效降低生产成本。
轧辊;成批更换策略;视情修磨; 备件订购策略;仿真;优化
随着经济的不断发展,钢铁的需求量也不断增加。作为轧钢工业的关键部件,轧辊是使轧材产生塑性形变的主要工具,也是轧制过程中的主要消耗部件。轧辊的可靠运行直接关系到钢材的产量和质量。
通过研究轧辊的维修特性与运行特征,结合现有的维修与库存策略,可把轧钢厂的一条生产线上的轧辊看作一个串联的同类多部件可修系统。
对于独立同分布的同类可修多部件组成的系统的最优维修优化问题,国内外已有诸多研究涉足:Osaki[1]研究的成批更换策略适用于多设备系统,该维修策略是指系统中所有的部件在等间隔时间点kTr(Tr固定,k=1,2,…)上进行周期预防更换,如果其他时间系统发生故障则立即进行故障后更换,并且任何故障后更换都不影响周期预防更换策略。俞金松等[2]从费用和可用度两个角度对成批更换的更换周期进行了分析和优化。Guo等[3]采用Wiener过程对系统对系统劣化进行建模,研究了任务限制系统的视情维修问题。Wang等[4]以舰队的船用柴油机油样,对基于寿命分布的视情维修进行了研究。Acharya等[5]早在1986年就研究了成批更换策略与(R,S)备件库存策略的联合优化问题。Wang[6]研究了定期预防维修和备件库存策略的联合优化问题。张晓红等[7]针对可修复杂关键组件研究了周期性视情更换式维修与连续检查的(S,s)备件订购联合优化策略。
通过研究多个独立同分布的同类可修多部件系统特性,结合轧辊自身的特性,本文采用周期性成批更换和视情修磨相结合的维修策略与(S,s)备件订购的联合策略,考虑维修时间和可修磨轧辊非完美维修的同时,分析了维修和备件之间的关系,建立了以单位设备在无限时间范围内的平均费用率为目标,以更换周期、报废阈值和库存参数为决策变量的随机仿真模型,采用离散时间仿真与遗传算法相结合的方法对模型进行求解。
1 系统特征
1.1 系统特征的定义
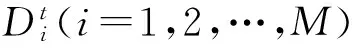
1.2 维修与备件库存的联合
采用周期性成批更换与离线视情修磨与(S,s)备件订购的联合维修策略,即生产线运行到需要更换的时刻,成批更换M个轧辊(优先更换直径大的),把更换下的轧辊统一送到修磨厂,并检测轧辊直径状态进行视情修磨。为了保证生产的持续和避免产生更高的持有成本,采用(S,s)备件策略,其中,s为安全库存水平,S为最大库存水平。设初始运行时,系统中有M个全新的轧辊,库存中有S个全新备用轧辊,并有专门的修磨厂可提供所有的轧辊修磨工作。在具体的系统运行过程中,由于维修与备件库存的相互制约和影响,预定的更换周期可能因备件不足而推迟,备件的库存和订购需求及数量也由维修活动的不断进行而动态更新。具体的维修与备件库存联合策略如下:
1) 周期性成批更换策略
本文采用成批更换维修策略,即系统在上次更换后等间隔时间T后进行周期性更换。第j个更换时刻tj对生产线上的M个轧辊进行更换,更换能否顺利完成与库存轧辊数量有关,设此时现有库存轧辊数量为SLj:
若SLj≥M,则更换立即完成,一次成批更换的费用为Cr,由于更换时间远小于系统的更换周期,因此假设更换瞬时完成;
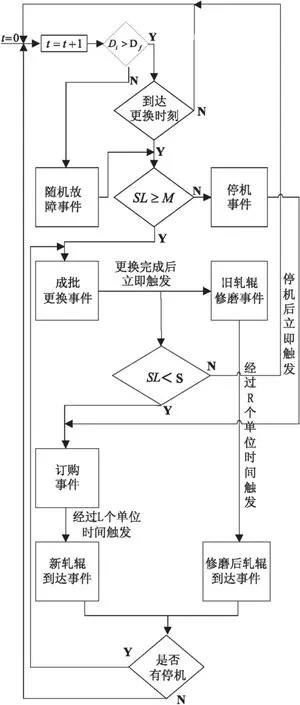
若SLj 2) 随机故障成批更换 在第j个和第j+1个周期性更换之间的tf(jT 3) 视情修磨策略 4) 备件库存和订购策略 设tj时刻修磨好的M′j个轧辊可补充到库存备用,但随着生产的继续,不可修复辊的不断报废,库存中可用轧辊数量不断减少,则第j 次更换后的系统中总的可用轧辊数量为SLj-M+M′j.根据定义的库存策略,若SLj-M+M′j 以单位轧辊无限时间范围内系统维修和库存轧辊总成本的平均费用率EC∞最小为目标,用于评价所提出联合策略的优劣。由1.2节的联合策略可知,轧辊更换周期T的太大可能造成轧辊欠维修,太小可能造成过维修;报废阈值Df太大则无法保证轧制钢材的质量,太小轧辊有效寿命得不到充分利用;库存参数S太大可能产生更多的持有成本,s太小无法维持生产线正常运行。因此要权衡决策变量T,Df,S,s,来确定最优的联合策略。 基于维修和备件策略联合优化问题的复杂性,建立目标与决策变量之间的解析函数比较困难,本文拟建立仿真模型,利用蒙特卡洛方法,对生产线上的M个轧辊在Tm个单位时间内的运行情况进行仿真。并建立了最低费用率fEC和决策变量T,S,s,Df之间的仿真模型。 (1) 3.1 离散事件仿真 分析建立的仿真模型发现,离散时刻不同事件的发生触发模型中所有统计量和费用成本的产生,整个仿真过程为离散事件仿真,一次仿真流程图如图1所示。 系统仿真开始,输入系统的参数有轧辊数量、报废阈值常量、各种成本常量、新轧辊交付时间、旧轧辊维修时间、劣化分布参数、视情修磨参数、更换周期、最大仿真时间和库存参数。每次仿真开始均需要初始化系统和库存状态、各类统计量、仿真时间、时间表等参数。整个仿真过程的离散事件分析如下: 1)周期性成批更换事件 图1 一次离散事件仿真流程图 Fig.1 The simulation flowchart of a discrete event 生产线运行Tm个单位时间,周期性成批更换引起的更换事件的总次数为Qr: (2) 2)旧轧辊修磨事件 tj时刻完成更换,检测更换下来的M个轧辊的直径,检测后可修磨轧辊数量为M′j.那么仿真运行Tm个单位时间后完成修复轧辊数量为 (3) TR=tj,经过R个单位时间触发修磨备件的到达事件,轧辊的维修不改变库存状态。 3)新轧辊订购事件 tj时刻需要订购新轧辊,订购次数FOj和订购数量NOj的计算如式(4)和式(5)所示,仿真运行Tm个单位时间后总的订购数量如式和式(6)所示。 (4) (5) (6) 若NOi>0,则修改订购参数SO=1,TLO=tj,NLO=NOj.经过L个单位时间触发新备件到达事件,轧辊订购不会引起库存状态变化。 4)新轧辊到达事件 将新轧辊插入到备用轧辊队首,tj时刻到达的新轧辊数量: (7) 式中,SO为订购标志;TLO为最后一次订购开始的时刻;NLO为最后一次订购数量。新轧辊到达后,库存状态发生变化SLj=SLj+NOSj,若系统运行标志位SR=1,则筹划周期性成批更换事件。一旦新轧辊到达,即NOSj>0,订购参数SO,TLO,NLO就全部恢复为0,TS=tj. 5)修磨后轧辊到达事件 将修好的轧辊按照直径从大到小的顺序插入可用库存,tj时刻到达的修好的轧辊数量: (8) 式(8)中,TR为最后一次修理开始时刻。修磨轧辊到达后,库存状态发生变化SLj=SLj+NCSj,TS=tj.若系统运行标志位SR=1,则筹划周期性成批更换事件。 6)停机事件 系统运行标志位SR置1,tj时刻停机,则停机时间 (9) 式(9)中,TS为新轧辊或者退化轧辊达到的时间。 7)随机故障事件 生产线运行Tm个单位时间,突然故障引起的更换事件总次数Qf (10) 事件之间的相互触发关系如图2所示。 图2 离散事件及其关系图 Fig.2 The diagram of discrete event and its relationship 3.2 遗传算法优化 遗传算法是一种基于生物自然选择与遗传机理的随机全局搜索算法[8]。其搜索依据概率算法,可有效避免局部最优结果的产生,广泛应用于组合优化的研究,因此本文用遗传算法优化上文所建立的离散事件系统仿真模型。 4.1 实验数据 设置单次仿真的运行周期Tm=500(hour)表1所示为M=5,T=6,Df=1 000,S=11,s=4时任意5次仿真结果所对应的周期性成批更换次数Qr,故障更换次数Qf,修磨轧辊总数量M,轧辊总持有数量Ch,总停机时间TDS,订购总数量Qo和费用率。 表1是多次仿真任选的5次仿真结果,多次仿真结果表明费用率比较稳定。 表1M=5,T=6,S=11,s=4是对应的5次仿真结果 Tab.1 The simulation results whenM=5,T=6,S=11,s=4 次数QrQfMChTDSQo费用率1761338345752814216782817378460531145162137893944842221331647.4478123784321351511650.2577123874365241371606 4.2 优化结果 遗传算法优化参数设置:种群大小为10,最大遗传代数为50,代沟0.8,交叉概率为0.8,变异概率为0.2.图3为M=5时的一次优化结果,优化后最小平均费用率为 1832.800 000,最优解为T=6,Df=1054.333 333 3,S=3,s=1.图4为M=56时的一次优化结果,优化后最小平均费用率为1 822.000 000,最优解为T=7,Df= 1001.742 096,S=21,s=16.优化结果表明平均费用率没有随生产线轧辊数量的增加而发生明显变化。 4.3 实验分析 由4.2节结果可以看出生产线上轧辊总数量的多少对更换周期的影响比较小,都在T=6左右。按照轧辊直径在单位时间内的劣化量为20 mm计算,生产线运行到更换时刻,轧辊直径消耗大约为120 mm,是报废差值(250 mm)的一半,优化后的更换周期有效的避免了过维修或欠维修的现象,所以论文制定的联合策略比较合理。 与太钢用到的经验更换周期T=3,本文采用联合策略所得到的最优更换周期T=6既减少了停机次数避免了过维修现象,又没有造成欠维修现象。 当M=5时,库存参数为S=3,s=1,最大库存约为生产线上轧辊总数量的1/2;当M=56时,库存参数为S=21,s=16,最大库存量为轧辊总数量的1/3,由此可见,对系统维修与备件库存联合优化的必要性,在保证较为稳定的费用率的前提下,不同系统的最优策略不尽相同。 遗传算法参数选择:种群数量太小不利于求得最优解,而太大相应的计算量也会增加;要想获得相对集中的最优解,就得减小变异概率,增加交叉概率。因此设置遗传算法种群大小为10,最大遗传代数为50,代沟0.8,交叉概率为0.8,变异概率为0.2. 图3 M=5时优化图像 Fig.3 The optimize image when M=5 图4 M=56时优化图像 Fig.4 The optimize image when M=56 提出的同一生产线上多个同类轧辊组成的可修多部件系统的成批更换及离线视情修磨与(S,s)备件订购的联合优化策略。与轧辊的实际特性结合,分析了轧辊维修和备件策略之间的权衡关系,考虑到连续劣化轧辊的非完美修磨效果、确定的交付时间和修磨时间,建立了以更换周期、报废阈值和维修参数为决策变量,以单位轧辊无限时间范围内的平均费用率最小为目标的仿真优化模型。 下一步将建立维修、库存和维修能力三者之间的模型。考虑更加是实际的系统策略和假设,如修磨时间,加急订购,随机交付时间,修磨效果等。 [1] OSAKI S. Stochastic models in reliability and maintenance[M]. Germany : Springer, 2002. [2] 俞金松, 程继红,张国. 导弹定时更换周期决策建模及仿真[J]. 舰船电子工程, 2013(8):94-97. [3] GUO C., W. WANG B. GUO,X. SI. A main-tenance optimization model for mis sion-oriented systems based on Wiener degradation[J]. Reliability Engineering & System Safety, 2013, 111(3):183-194. [4] WANG W., B. HUSSIN,T. JEFFERIS. A case study of condition based maintenance modelling based upon the oil analysis data of marine diesel engines using stochastic filtering[J]. International Journal of Prod-uction Economics, 2012,136(1):84-92.[5] ACHARYA D., G. NAGABHUSHANAM,S. ALAM. Jointly optimal block-replacement and spare provisioning policy[J]. Reliability, IEEE Transactions on, 1986, 35(4):447-451. [6] WANG W. A stochastic model for joint spare parts inventory and planned maintenance optimisation[J]. European Journal of Opera-tional Research, 2012, 216(1):127-139. [7] 张晓红,曾建潮. 可修组件的视情更换维修与备件订购联合优化[J]. 计算机集成制造系统, 2014(4):909-918. [8] 洪朝飞,陶元芳,潘鲜.面向机械设计的一种改进遗传算法[J].太原科技大学学报,2013(4):101-106. The Joint Optimization Strategies of Rollers Maintenance Policy and Spare Parts Provisioning Policy GAO Kun, ZHANG Xiao-hong, ZENG Jian-chao (Taiyuan University of Science and Technology, Taiyuan 030024, China) Roller is an important tool for plastic deformation of rolling material and the main consuming parts in Rolling Industry. Reasonable replacement policy and spare parts inventory are essential to ensure production and reduce production costs. Taking the roller system in roll machine as a multi-unit with many identical units and combining the characteristic of roller, a joint optimization strategy of roll block replacement policy and condition-based repair and (S,s) type spare parts provisioning policy was proposed. Based on the assumptions of deterministic maintenance time, lead-time and imperfect maintenance effect, the relationship between maintenance policy and spare parts inventory strategy was analyzed. On this basis, the simulation optimization model was established with trashed threshold and inventory parameter as the decision variable and minimum average cost rate in infinite time range as the target. The discrete event simulation and genetic algorithm were used to solve the model. The results of simulation indicated that the joint optimization strategy could be got, and the proper retirement threshold and inventory parameter can decrease maintenance cost significantly. roller, block replacement policy, condition-based repair , (S,s) type spare parts provisioning policy, simulation, joint optimization 1673-2057(2016)06-0462-07 2016-01-04 国家自然科学基金(61573250) 高坤(1988-),男,硕士研究生,研究方向为系统健康管理。 TH165+.3 A 10.3969/j.issn.1673-2057.2016.009
2 模型的建立
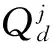
3 模型求解
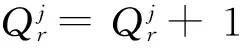


4 算例分析
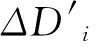



5 结束语
——基于教育培训行业的实证分析

