放坡疏浚对海陆交接段隧道稳定性的影响研究

陈向红， 陶连金， 刘春晓， 安林轩， 安军海

(北京工业大学建筑工程学院， 北京 100124)



放坡疏浚对海陆交接段隧道稳定性的影响研究

陈向红， 陶连金， 刘春晓， 安林轩， 安军海

(北京工业大学建筑工程学院， 北京 100124)

为了研究航道疏浚对水下隧道结构的影响，选取海陆交接处的隧道段作为分析对象，考虑隧道围岩为基于Drucker-Prager屈服准则的连续介质，利用ANSYS有限元软件分析了航道疏浚对结构变形、受力的影响，重点对航道放坡疏浚条件下放坡坡度、回淤厚度及疏浚工序等因素的影响程度进行了研究。数值计算结果表明：航道疏浚清淤增加了沿隧道纵向的差异变形，且影响较大的水域段最大竖向位移发生在隧道顶部，而最大等效应力则出现在隧道两侧；航道疏浚放坡坡度大小除了与坡体本身的稳定性相关外，在水深一定条件下，坡度的改变对结构水域段和陆域段的影响甚微，主要影响到放坡段的结构变形和内力变化速率，实际工程中应综合经济性评价与效果分析确定疏浚坡度的取值；此外，回淤、再清淤厚度对结构变形和内力的影响也是航道规划、设计中需要考虑的主要问题。

水下隧道； 航道放坡疏浚； 坡度系数； 回淤厚度； 数值模拟

0 引言

近年来，作为一种新型环保的跨水域交通手段，水下隧道在国内外不断得到开发，并持续向着长大化深度发展[1]。然而，由陆地水系携带的泥沙等冲填物常在水底形成深厚淤积层，从而堵塞航道、污染水质，需要定期清淤以满足正常通航，维护河流生态环境[2-3]，同时考虑航道开挖可能引起的隧道过大上浮等风险[4-5]，合理规划航道，调查航道施工对水下隧道稳定性的影响，是目前亟待解决的研究课题。

近几年来，国内外有关航道开挖对水下隧道的影响研究常见于沉管隧道[6-9]，而对于深埋盾构隧道的影响研究较少。其中，黄俊等[10]采用数值模拟方法分别研究了航道疏浚深度、疏浚工序及回淤厚度对海底盾构隧道结构纵向变形和受力的影响；王道远等[11]则基于弹性地基梁弯曲模型，对运河开挖卸荷下的隧道纵向上浮量进行了预测研究。上述学者尽管对水下盾构隧道的航道施工工况进行了一定研究，但未考虑航道疏浚放坡坡度的影响问题。当前，随着国内各港口(长江口和珠江口等)、琼州海峡、台湾海峡通道的前期规划、研究和设计工作的相继开展，海底隧道工程的结构稳定性问题日益凸显。鉴于此，本文针对妈湾盾构隧道海陆交接段的结构稳定问题，通过数值模拟方法，开展了疏浚放坡坡度、回淤厚度和施工步序等因素对隧道结构变形和内力的影响分析研究。

1 工程概况

拟建妈湾隧道为深埋式盾构公路隧道，主要承担南山港区的疏港货运交通。航道测试水深约5.0 m；远期航道底高程-19.3 m(黄海高程系)；盾构隧道埋深为规划航道下方10 m，设计外径为φ15 m，壁厚0.65 m，环宽2 m，左、右线净间距为15 m；陆地高出自由水面约5 m，为确保岸边结构的稳定，航道采用放坡疏浚方案，航道疏浚断面见图1。

图1 航道疏浚断面示意图

Fig. 1 Cross-section showing channel dredging

由地质勘查报告，该段土层从上至下依次为人工填石(素填土)、淤泥、中粗砂、全-强风化花岗岩、中-微风化花岗岩。

2 模型与结果分析

2.1 模型尺寸、参数及假定

本文针对妈湾隧道海陆交接段结构，采用ANSYS软件进行模拟，计算模型如图2所示，模型尺寸沿隧道纵向水域段与陆域段各取值100 m，宽度方向取半结构(边界距离隧道近端一侧为5D，D为隧道直径)，坡段宽度根据放坡坡度确定。模型上方取至地层自由面，下至隧道底以下80 m(约5D)；隧道和围岩均采用六面体实体单元，底边界限制竖向位移，左边界与前后边界限制水平位移，右边界为对称边界。拟建隧道深埋在具有一定结构性的花岗岩地层，参照志波由纪夫的等效连续模型，将隧道简化为具有等效刚度的均匀线弹性体[12]；淤泥介质则按非牛顿流体以静压力作用在规划航道底面[13-14]。计算时通过对淤泥压力和静水压力相互转化，以实现清淤和回淤的过程模拟。假设在海陆交接位置的地层近似呈水平分布，不计岩层中水的渗流和浮力影响，选用符合Drucker - Prager准则的弹塑性本构模型。由地质勘查报告和隧道方案资料，围岩与结构参数见表1和表2。

图2 海陆交接段三维计算模型(单位：m)

Fig. 2 3D calculation model of land-sea connecting area(m)

表1 地层计算参数

Table 1 Calculation parameters of strata

地层名称h/mE/MPaμγ/(kN/m3)c/kPaφ/(°)人工填土(石)15100.319220淤泥1016.4中粗砂6180.3520030全-强风化岩121000.32223225中-微风化岩4725400.22560040

表2 支护结构计算参数

Table 2 Calculation parameters of supporting structures

材料类型 t/mE/MPaμγ/(kN/m3)隧道管片0.65345000.225浆液结石体2.52000.2523

考虑到结构分析断面应具有代表性，用于隧道结构变形与内力分析的观测点布置如图3所示，观测点分别选择在距离模型前后边界40 m、航道疏浚前水底、航道坡顶及坡脚位置处。

图3 隧道分析截面位置示意图(单位：m)

Fig. 3 Location of analytical sections of tunnel(m)

2.2 模型比较

为验证有限元模型计算结果的可靠性，首先与Winkler弹性地基梁模型作对比，梁计算长度包括水面以下坡段和水域段部分。根据表1和表2所列参数，依据Vlazov理论[13]定义隧道计算段基床系数均取10 000 kN/m3，隧道纵向等效抗弯刚度EI= 1.668 × 1010kN·m2，隧道单位长度受到的静态上浮力按清淤引起的卸载大小考虑，当清淤厚度为10 m、边坡坡度系数为1∶2时，水域段上浮力为64 kN，坡段按三角形荷载由水底位置向坡脚逐渐递增，采用与文献[11]相同的边界条件设置。由此求得Winkler理论解与数值解的比较结果如图4所示。

图4 隧道纵向上浮曲线

Fig. 4 Curve of longitudinal uplifts of shield tunnel

由图4分析可知，由于简化处理时坡段地基反力系数取值与水域段相同，以及未考虑地层间的水平剪力传递效应，理论解明显偏高。但在远离坡段位置，最大上浮量误差为2.98%，理论解和有限元数值解所绘制的曲线几乎重合，且沿隧道结构纵向上浮量变化规律与文献[10]和文献[11]中隧道两头的分析结论一致。

2.3 隧道结构受力分析

航道疏浚前后隧道截面最大竖向位移与等效应力沿隧道纵向的分布规律如图5和图6所示。

分析图5和图6中曲线可知：

1) 航道疏浚前后，由于航道的开挖卸荷作用，水域段隧道出现较明显的抬升，沿隧道纵向最大上浮量为3.12 mm，沿隧道坡段周壁任意点的位移梯度为0.02%，满足变形限值要求[15-16]。

2) 沿隧道纵向最大等效应力为14.5 MPa，最大等效应力差则由4.25 MPa增至5.87 MPa。结构最大等效应力变化值为1.62 MPa，满足隧道管片材料强度要求。

3) 由于航道开挖边坡的影响，海陆交接段的连接长度增加，隧道位移和等效应力由陆域向水域呈近似抛物线式平缓发展；由于清淤引起的结构受力变化，隧道响应曲线由近陆域部分的凸曲线逐渐过渡为近水域部分的凹曲线。

4) 当疏浚放坡坡度系数较大，坡道较陡时，水-土、水-气之间材料属性差异对隧道结构变形和应力发展的影响不显著。

图5 航道疏浚前后隧道纵向最大竖向位移分布

Fig. 5 Distribution of maximum vertical displacements of tunnel before and after channel dredging

图6 航道疏浚前后隧道纵向最大等效应力分布

Fig. 6 Distribution of maximum equivalent stresses of tunnel before and after channel dredging

1#和5#观测点沿隧道截面环向各点相对起拱线竖向位移与等效应力分布规律如图7和图8所示。

(a) 1#观测点

(b) 5#观测点

Fig. 7 Relative displacement distribution of spring line on tunnel cross-section

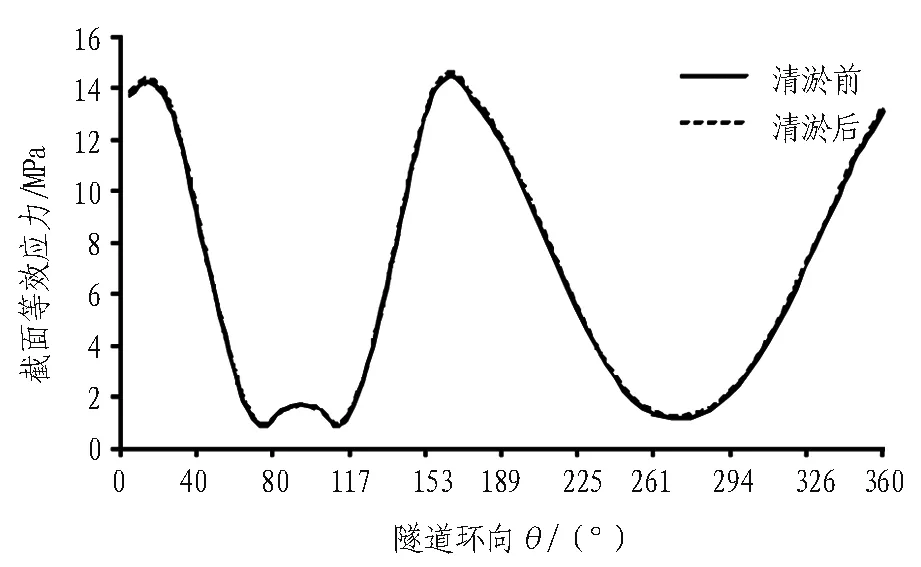
(a) 1#观测点

(b) 5#观测点

Fig. 8 Equivalent stress distribution on tunnel cross-section

从图7和图8可以看出，航道疏浚前后，沿隧道截面环向各点竖向位移和等效应力受影响较大位置均出现在水域段。其中，位移最大位置发生在隧道拱顶，拱底则产生与拱顶反向的变形；受三向应力状态影响，结构最大等效应力出现在隧道两侧。

3 航道放坡疏浚方案的参数影响分析

3.1 放坡坡度的影响关系

其他条件不变，不同疏浚坡度下隧道截面最大竖向位移和等效应力的分布规律如图9和图10所示。

由图9和图10计算结果可知：

1) 当坡度系数由1∶2减小至1∶10时，隧道截面沿纵向最大竖向位移和等效应力变化趋于平缓，由陆域向水域发展的过渡效应逐渐减弱。由此可见，减缓航道疏浚放坡坡度在一定程度上减弱了直立边坡或大坡度陡坡引起的应力集中现象，缩减结构节点处理开支。但从另一角度看，边坡的无限放缓也限制了航道的开发和岸边的充分利用。因此，需要合理的规划航道坡度以满足结构稳定性和空间使用效率的双重要求。

2) 随着坡度放缓，航道放坡段结构纵向最大竖向位移和等效应力分布曲线受上覆水和淤泥等介质材料的属性影响越显著。隧道反应曲线由较明显的“凸-凹”单拐点曲线逐渐向着多拐点、多段线的连接方式转换，曲线曲率亦随之减小。

3) 在航道边坡坡顶和坡底位置，结构反应变化速率较大，需要对坡段两端位置处地层与结构的加固方式及效果做进一步研究。

图9 不同坡度下隧道纵向最大竖向位移分布

Fig. 9 Distribution of longitudinal maximum vertical displacements of tunnel under different dredging gradients

图10 不同坡度下隧道纵向最大等效应力分布

Fig. 10 Distribution of longitudinal maximum equivalent stresses of tunnel under different dredging gradients

3.2 回淤厚度的影响关系

航道疏浚后一段时间内均有回淤，分别对2～9 m的回淤厚度进行分析，不同回淤厚度下各测点最大竖向位移、等效应力变化趋势如图11和图12所示。

由图11和图12分析可知：

1) 当回淤厚度由2 m增至9 m时，结构最大竖向位移和等效应力与之基本呈线性增长关系，且受回淤厚度影响较大位置均发生在水域段(4#、5#)。

2) 航道回淤、清淤属于“加载—卸载—再加载再卸荷”的循环过程，需要通过优化结构和地层参数来降低由于荷载变化对隧道稳定性产生的不利影响。

图11 不同回淤厚度下各测点最大竖向位移变化规律

Fig. 11 Maximum vertical deformation of tunnel measured at different monitoring points under different back-silting depths

图12 不同回淤厚度下各测点最大等效应力变化规律

Fig. 12 Maximum equivalent stresses of tunnel measured at different monitoring points under different back-silting depths

3.3 施工步序的影响关系

航道清淤、回淤2 m及二次清淤施工步序下各测点最大竖向位移与等效应力相对疏浚前的增幅变化规律如图13和图14所示。

图13 各测点最大竖向位移增幅

Fig. 13 Amplification of maximum vertical deformations of tunnel measured at different monitoring points

图14 各测点最大等效应力增幅

Fig. 14 Amplification of maximum equivalent stresses of tunnel measured at different monitoring points

由图13和图14可知，位于水域段的5#测点和坡脚4#测点受航道疏浚的影响最大，其中，由清淤引起的最大竖向位移和应力增幅：5#测点为-11%和-15%，4#测点为-7%和-10%；回淤2 m后位移和应力有所回弹，二次清淤又再次使位移和应力接近航道清淤时水平。由此可见，控制回淤厚度不变，航道清淤后的结构变形和应力水平呈振荡变化。

4 盾构隧道加固方案

在水下隧道上方施工须满足国家及地方相关法律、法规的要求[17-18]。航道设计时应考虑在水下隧道防护地段设置禁止抛锚或疏浚等航行及施工警示装置，或考虑安全和经济性优化覆盖层厚度，以及对隧道进行防护加固等保护处理措施，以保障隧道施工与运营安全。

4.1 隧道结构加固方案

优化隧道衬砌几何和材料参数，以实现控制结构变形，达到减小沉降或防止过大上浮的目的。其中，使用高强度、高延展性新型材料和增加衬砌厚度，是提高结构抗弯刚度的有利举措； 但同时限制了隧道空间开发，增加振动荷载作用下的吸收能，对结构稳定和受力均不利。

海陆交接段的边坡坡角位置为应力集中区，最大相对位移亦出现在该区域，因此，可考虑设置大变形环，以缓冲差异沉降。

4.2 地层加固方案

由理论分析可知，在相同荷载作用下，地基反力系数越高，则支撑在地基上的结构变形量越小，尤其当原有地层反力系数小于10 000 kN/m3，地层加固后的影响效果越显著[11]。

对于本文中深埋于地基反力系数较高岩层中的隧道结构，为控制航道施工引起的过大上浮位移，除了必要的隧道衬砌壁后注浆外，一方面，从隧道内沿隧道径向打深孔锚杆桩，其中锚杆长度需大于岩层厚度，其目的是为了建立不同地层间的协同工作能力，提高地层整体抗弯刚度； 另一方面，从水底钻孔注浆加固地层，其目的同前者一致，钻孔深度以达到岩层并具有一定锚入深度为基准，注浆段厚度可通过参数分析和经济性评估确定； 但考虑水下施工难度较大，加固效果难以控制，同时对航道运营亦存在一定影响。

5 结论与讨论

本文针对航道放坡疏浚对水下隧道的影响开展了研究，通过与简化模型及文献计算隧道纵向位移分布规律的比较证明了本文方法的可靠性。所得结论如下。

1) 航道施工在隧道海陆交接处产生位移和应力差，在疏浚放坡段位移速率较大，朝着水域或陆域方向逐渐下降，因此，可通过在差异变形较大位置设置大变形环或优化地层注浆参数，以缓冲差异变形的不利影响。

2) 航道疏浚主要对水域隧道段产生较大影响，且受影响程度较大位置中最大位移发生在拱顶，而最大等效应力则出现在隧道两侧。

3) 航道疏浚坡度主要影响到放坡段的结构变形和内力变化速率，随坡度减小结构反应曲线趋于平缓，位移变化速率降低。但考虑到放坡坡度不能无限小，坡段位置仍然是今后水下隧道加固处理的重要环节。

4) 隧道结构变形和应力与回淤厚度呈近似线性关系，并随着回淤、再清淤的施工进展，其结构变形和应力水平呈振荡变化。

本文对航道放坡疏浚下隧道海陆交接段的稳定性问题进行了初步研究，相关的研究工作仍需结合更详细的地质水文勘察、安全评估报告和健康监测资料进行定量的分析和反馈，并根据结构变形控制指标指导施工，对可能存在的风险提出及时可行的加强处理措施和补救方案。

[1] 王梦恕. 水下交通隧道发展现状与技术难题——兼论“台湾海峡海底铁路隧道建设方案”[J]. 岩石力学与工程学报, 2008, 27(11): 2161-2172. (WANG Mengshu. Current developments and technical issues of underwater traffic tunnel: Discussion on construction scheme of Taiwan Strait undersea railway tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(11): 2161-2172. (in Chinese))

[2] 水玉跃, 丁天明. 舟山虾峙门口外航道疏浚对海洋生态环境的影响及防治措施[J]. 浙江海洋学院学报(自然科学版), 2012, 31(3): 249-255. (SHUI Yuyue, DING Tianming. The countermeasures and effects of the Zhoushan Xiazhimen’s waterway dredging programs to ocean ecology environments[J]. Journal of Zhejiang Ocean University (Natural Science Edition), 2012, 31(3): 249-255. (in Chinese))

[3] Erftemeijer P L A, Riegl B, Hoeksema B W, et al. Environ-mental impacts of dredging and other sediment disturbances on corals: A review [J]. Marine Pollution Bulletin, 2012, 64(9): 1737-1765.

[4] Azadi M, Mir Mohammad Hosseini S M. The uplifting behavior of shallow tunnels within the liquefiable soils under cyclic loadings [J]. Tunnelling and Underground Space Technology, 2010, 25(2): 158-167.

[5] ZHANG Z G, HUANG M S, WANG W D. Evaluation of deformation response for adjacent tunnels due to soil unloading in excavation engineering[J]. Tunnelling and Underground Space Technology, 2013, 38: 244-253.

[6] Rasmussen N S. Dredging for immersed tunnels: The designer’s and contractor’s viewpoint[C]// Central Dredging Association CEDA Dredging Days 1987. [S.l.]: ICE Publishing, 1987: 75-87.

[7] Grantz W C. Immersed tunnel settlements. Part 1: Nature of settlements [J]. Tunnelling and Underground Space Technology, 2001, 16(3): 195-201.

[8] Grantz W C. Immersed tunnel settlements. Part 2: Case histories [J]. Tunnelling and Underground Space Technology, 2001, 16(3): 203-210.

[9] 丁文其, 朱令, 彭益成, 等. 基于地层-结构法的沉管隧道三维数值分析[J]. 岩土工程学报, 2013, 35(增刊2): 622-626.(DING Wenqi, ZHU Ling, PENG Yicheng, et al. 3D numerical analysis of immersed tunnels based on stratum-structure method [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 622-626.(in Chinese))

[10] 黄俊, 张顶立, 刘洪洲, 等. 航道疏浚对海底盾构隧道纵向稳定性的影响研究[J]. 岩石力学与工程学报, 2007, 26(11): 2363-2369. (HUANG Jun, ZHANG Dingli, LIU Hongzhou, et al. Study of influences of channel dredging on longitudinal stability of subsea shield tunnel [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(11): 2363-2369.(in Chinese))

[11] 王道远, 王锡朝, 袁金秀, 等. 运河开挖卸载下水下盾构隧道纵向上浮量预测研究[J]. 现代隧道技术, 2015, 52(2): 110-114. (WANG Daoyuan, WANG Xichao, YUAN Jinxiu, et al. Prediction of the longitudinal uplift of an underwater shield tunnel during canal excavation [J]. Modern Tunnelling Technology, 2015, 52(2): 110-114.(in Chinese))

[12] 志波由纪夫, 川岛一彦, 大日方尚巳, 等. シールドトンネルの耐震解析に用いる長手方向覆工剛性の評価法 [C]//土木学会论文集. 东京: 土木学会, 1988: 319-327. (Shiba Y, Kawashima K, Obinata N, et al. An evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analyses [C] // Proceedings of Japan Society of Civil Engineers. Tokyo: Japan Society of Civil Engineers, 1988: 319-327.(in Japanese))

[13] 田琦. 河口淤泥特性及其运动规律研究[D]. 天津:天津大学, 2010.(TIAN Qi. The research on properties and motions of mud in estuary [D]. Tianjin: Tianjin University, 2010.(in Chinese))

[14] Jacob N, Ansari M A, Revichandran C. Environmental isotopes to test hypotheses for fluid mud (mud bank) generation mechanisms along the southwest coast of India[J]. Estuarine, Coastal and Shelf Science, 2015, 164: 115-123.

[15] 盾构法隧道施工与验收规范：GB 50446—2008[S]. 北京：中国建筑工业出版社，2008. (Code for construction and acceptance of shield tunneling method：GB 50446—2008[S]. Beijing：China Architecture & Building Press, 2008.(in Chinese))

[16] 公路隧道施工技术规范: JTG F60—2009[S]. 北京：人民交通出版社，2009. (Technical specifications for construction of highway tunnel: JTG F60—2009 [S]. Beijing：China Communications Press, 2009. (in Chinese))

[17] 公路水下隧道设计规范: JTG D71—2014 [S]. 北京：人民交通出版社，2014. (Specifications for design of highway underwater tunnel: JTG D71—2014 [S]. Beijing：China Communications Press, 2014. (in Chinese))

[18] 港口及航道护岸工程设计与施工规范: JTJ 300—2000[S].北京：人民交通出版社，2000. (Code for design and construction of port and waterway revetment engineering: JTJ 300—2000 [S]. Beijing：China Communications Press, 2000. (in Chinese))

Study of Influence of Grading and Channel Dredging on Stability of Subsea Tunnel in Land-sea Connecting Area

CHEN Xianghong, TAO Lianjin, LIU Chunxiao, AN Linxuan, AN Junhai

(CollegeofArchitectureandCivilEngineering,BeijingUniversityofTechnology,Beijing100124,China)

For studying the influence of channel dredging on underwater tunnel structure, taking subsea tunnel in the land-sea connecting area for example, the surrounding rock is modeled as continuous media based on Drucker-Prager yield criterion. The influencing degrees of the channel dredging, including the channel dredging gradient, the alluvium thickness and the dredging working procedure, etc, on tunnel structure deformation and stress are studied by means of finite element software ANSYS. The numerical calculation results show that: 1) The differential deformations along the longitudinal direction of tunnel is increased by channel dredging; the vertical displacement of tunnel roof at underwater section is the largest; and the equivalent stresses of the both sides of tunnel are the largest. 2) The grading gradient is related to slope; the change of gradient affects structure in land and water a little, and mainly affects the deformation and stress of structure in grading section. 3) The influence of back-silting and desilting thickness on structural deformation and internal force should also be considered in the channel planning and design phases.

underwater tunnel; grading and channel dredging; gradient coefficient; alluvium thickness; numerical simulation

2016-02-01；

2016-04-01

北京市市政工程设计研究总院有限公司委托横向课题(2014W063)

陈向红(1978—)，男，河北保定人，2013年毕业于北京交通大学，岩土工程专业，博士，讲师，主要从事地下工程领域的教学与科研工作。E-mail：07872@bjut.edu.cn。

10.3973/j.issn.1672-741X.2016.07.006

U 459.5

A

1672-741X(2016)07-0806-06