盾构地铁隧道区间在地震作用下的三维动力时程响应分析
毕 冉,唐 晓,刘保健
(1.长安大学公路学院道路与铁道工程,陕西西安 710064;2.中交公路第一公路勘察设计研究院道路与轨道分院,陕西西安 710075)
盾构地铁隧道区间在地震作用下的三维动力时程响应分析
毕 冉1,唐 晓2,刘保健1
(1.长安大学公路学院道路与铁道工程,陕西西安 710064;2.中交公路第一公路勘察设计研究院道路与轨道分院,陕西西安 710075)
地铁已成为城市地下空间结构和轨道交通网络的重要组成部分。为预估和降低地震灾害的影响,以西安盾构地铁区间隧道为例,建立了地铁隧道区间三维计算模型,进行三维抗震时程响应分析。采用粘弹性局部人工边界模拟地基结构的半无限性,利用不同超越概率水平下的地震动参数作为参考,考虑相位随机性影响,拟合地震动时程样本,建立了地基与结构相互作用的三维有限元模型。计算结果表明,地震发生时,顶部、底面、侧面、以及联络通道处虽产生变形影响,但均在规范规定范围内;位移时程曲线、位移分布云图、拉压应力云图清楚显示区间结构在地震持续时的抗震情况,数据表明结构最不利位置在联络通道处,而内力和变形均满足规范安全要求。
地铁区间 地下空间结构 抗震 三维计算 地震相应 时程分析
1 引言
相对于地上结构来说,普遍的认知是地下结构较为良好的抗震性能,虽然在周围土体的约束下存在一定程度的抗震优化作用,但根据过往的地震灾害历史记录显示,被认为良好的地下空间结构在地震作用下也会发生严重的破坏,威胁人的生命和财产安全,像是1995年在日本阪神地震作用导致大规模地下结构破坏,其中地铁车站的威胁甚大,支撑结构坍塌,车站沉降远超安全水平,发生严重破坏(Horibe,1995;Uenishi,2000;Liu,2006)。1994年的美国Northridge 6.7级地震,1999年台湾的集集地震和土耳其Kocaeli地震,2003年伊朗Bam地震等,由于距离城市较近,对人口相对密集的居民造成了严重伤害。近年来,随着市政公路网线的快速发展,城市地面发展的有限空间轨道成为制约城市发展的不利因素,地铁网络应运而生,地震活动诱发的地下空间结构稳定性问题,如引发岩土工程突水、涌水、
裂缝等(谢云跃等,2015;袁广祥等,2015),成为隧道工程施工关注的热点问题。地下空间结构也越来越在城市居民生活中占据举足轻重的地位。
本文以西安地铁沿线某地下二层双柱三跨箱形框架结构区间为例进行时程地震反应分析,其中对地基开放系统到封闭系统的实现是通过黏弹性边界的施加来保证,且考虑到侧向人工边界的合理性,选取范围顶至地表面,低至设计地震作用基准面,水平向侧壁距离边界至少大于水平有效宽度三倍。虽然地下车站区间结构形式连续,横截面构造大致相同,土层沿纵向分布也较为一致,抗震验算可以化简为只考虑只沿着横向计算水平地震作用,抗震分析也可以按照平面应变问题分析,但为了更加精确的模拟地铁区间的地震响应,仍对其进行三维建模分析,边界选取粘弹性局部人工边界(Choietal.,2002),混凝土的本构模型采用(Jeeho,1998)动损伤模型来计算地震作用对地铁结构的影响(刘晶波等,1998;国胜兵等,2002;匡志平等,2002)。
2 有限元粘弹性局部人工边界分析
地铁地基结构系统是一个无限开放的系统,无论是针对地铁采用静力还是动力分析,都涉及到对半无限地基辐射阻尼的模拟。静力分析时,可以通过增大地基取值范围来实现;但动力分析时,为了避免计算模型尺寸过大造成计算负担,影响有效计算速率,或者计算模型尺寸过小,导致散射波在截取的有限边界区域上发生反射增大计算误差,因此选用粘弹性局部人工边界。
粘弹性局部人工边界从粘弹性角度考虑,一方面克服了粘性边界在模拟地基弹性恢复性能时的误差,避免了低频漂移情况,体现出良好的频率稳定特性;另一方面考虑了散射波能的吸收,便于与大型商业软件的二次开发进行对接(Deeks,1994;刘晶波等,2006;谷音等,2007),计算精度满足工程研究需求。从局部人工边界角度来说,具有良好的时空解耦特性,实现简便,虽然全局人工边界,如边界元计算精度较高,但由于全局耦合特性,计算耗时长,因此局部人工边界从计算时间和适用性角度分析都具有更广的应用范围(Lee,1998)。具体来说,粘弹性局部人工边界是通过在边界上设置阻尼器和弹簧来实现的,三维局部人工边界的法向和切向刚度计算如下:
其中,αN表示法向粘弹性局部人工边界修正系数;αT表示切向粘弹性局部人工边界修正系数。经过大量算例验证粘弹性人工边界鲁棒性良好,法向和切向粘弹性局部人工边界修正系数取值范围在0.5~1.0和1.0~2.0之间计算结果精确度较高,经数值分析本文将αN和αT分别设置为0.68和1.35(Huoetal.,2013);G表示土的剪切模量;R表示波源到局部人工边界点的距离。
法向和切向阻尼系数为:
其中,ρ表示土体的密度;vp表示土体的P波;vs表示土体的S波;Ai表示局部人工边界上节点所代表的面积。
3 地铁地震动荷载有限元实例分析
以西安市在建地铁某盾构区间主体结构为研究背景,区间隧道设计里程为右CK21+851.863-右CK22+513.082;左CK21+851.863-左CK22+513.082。右线全长661.219m,左线全长661.538m,区间采用盾构法施工,并且在右CK22+135.000处设置区间联络通道兼废水泵房(此处联络通道属于抗震薄弱部位),隧道埋深为11.1m~14.3m,采用浅埋暗挖施工。区间纵断面先以1.3%的坡向下至联络通道及泵房后,再以0.6526%的坡向上至站二,穿越的土层主要为黄土状土、粉质粘土和中砂。隧道有限元模型见图1,纵长90m,宽100m,高度75m,由于采用动力分析,在设定单元尺寸时为了考虑地震波的传播,剪切波传播方向的单元长度需要满足:
(3)
式中:λmin计算考虑最短波长,鉴于地震波能量集中在0~50Hz范围内,因此当土体最小剪切波速为100m/s时,λmin为10m,此时单元尺寸不大于1m即满足计算要求。本文土层最小剪切波速约为180m/s,故单元尺寸经计算不超过2.3m即满足要求。网格划分尺寸设为2.0m,符合要求,模型包括共60086个单元,61640个节点,三维模型如图1所示。

图1 区间隧道有限元模型
3.1 介质的动力本构模型
土体和地铁结构混凝土在地震等动荷载的作用下的非线性特性是反映地震风险分析的一个重要影响因素之一,因此对于土体本构模型的选取必须可以反映在地震动荷载的作用下非线性、滞后性和累计变形,本文通过修正的Davidenkov粘弹性动力本构模型来实现有效孔隙水压力和体积应变的变化(宫必宁等,2002);结构所用混凝土的动力本构关系通过Jeeho(1998)提出的粘塑性动力损伤模型实现。场地土体动力参数见表1所示,地铁区间设计地震分组为第一组,场地类别为Ⅱ类,特征周期值是0.39s,抗震设防分为为乙类,抗震等级为二级,无液化,没有地裂缝,各土层分布相对稳定,无明显错断,无湿陷性黄土,按照抗震设防烈度8度进行抗震验算(杨林德,2003)。同时盾构法使用的装配式钢筋混凝土管片材料使用C50混凝土,管片厚度300mm,管片宽度1500mm。

表1 土体的力学参数Table 1 Mechanical parameters of soil
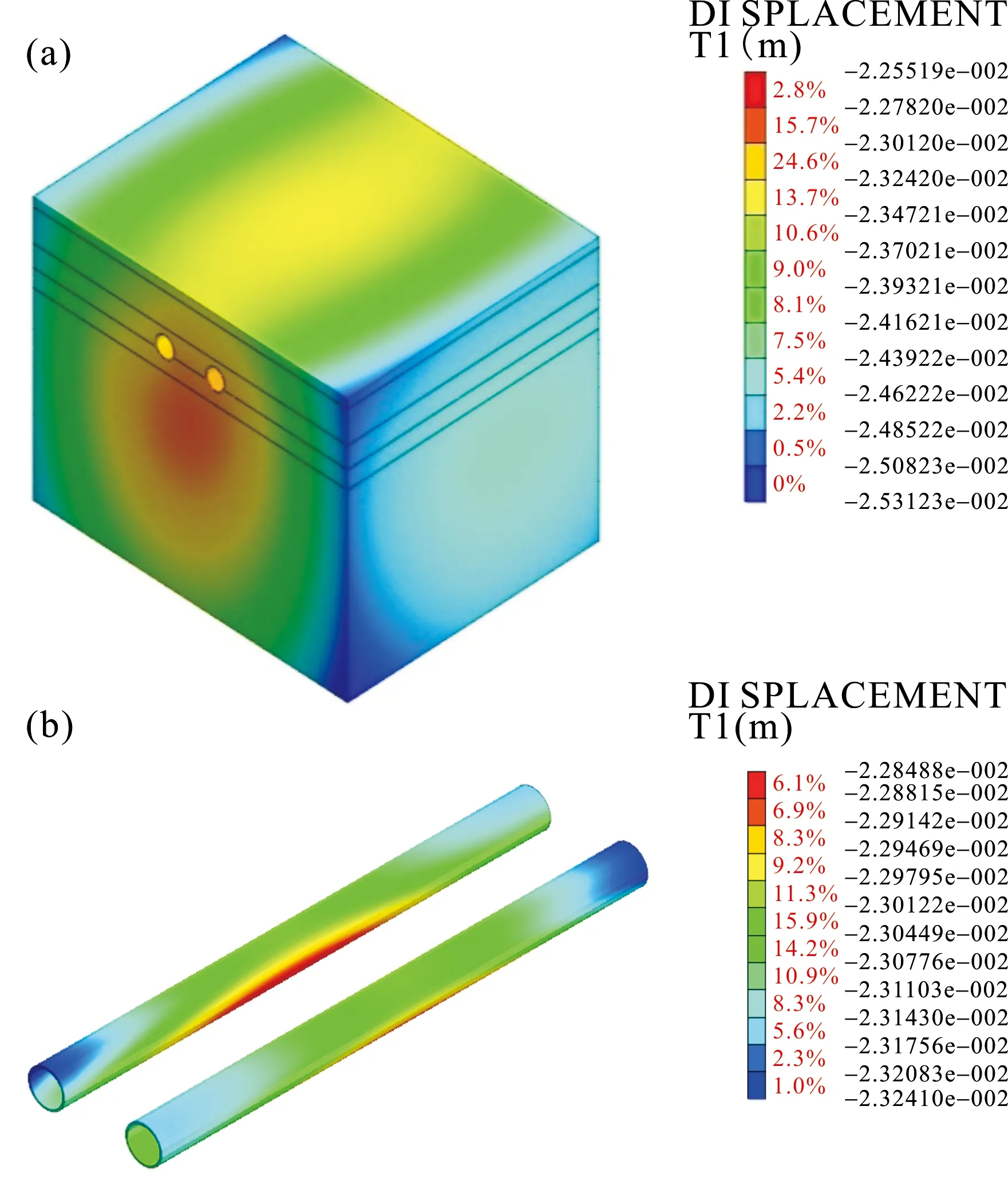
图2 地震作用下位移云图
3.2 地震波构造
地铁工程位于渭河断陷带内,并涉及到秦岭褶皱系的北部边缘,根据地铁地震安全评估报告中给出的场地基岩地震相关反应谱为依据,利用50年超越概率为10%和2%的地震动参数合成模型地震动时程,将地震运动视为一个随着时间变化的过程进行计算分析。其中因为地震波直接输入的关系,土体单元的尺寸要受到一定限制,利用振波的高频成分决定网格单元长度,低频成分决定模型边界范围的大小,考虑到水平向和竖直向地震波的影响,侧局部人工边界距离地下结构为三倍地下结构水平有效宽度,地面局部人工边界取自地震作用基准面,上表面取自实际地表。
3.3 计算模型
3.3.1 地震作用下的变形结果
分别考虑三组地震加速度反应谱,计算结果取其包络值。地震作用时,地层横断面X方向的最大的位移是22.6mm,发生在时间5.5s处;区间隧道结构的X方向最大位移是22.8mm。从地层结构和区间结构的位移云图(图2)可以得知,地层峰值位移小于区间峰值位移,结构的峰值位移在地铁区间中点位置,故中点位置较其他结构属于较为薄弱环节。
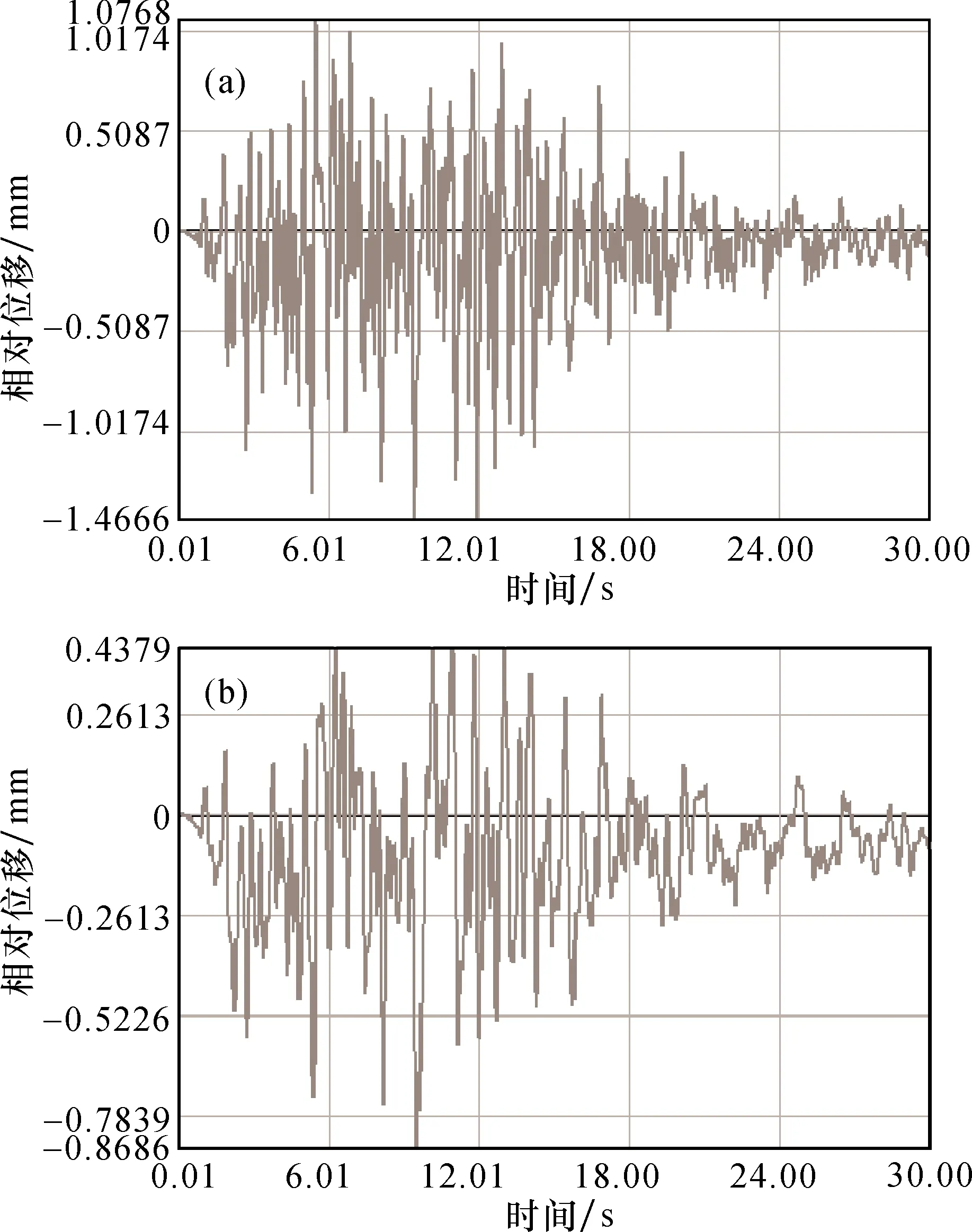
图3 区间隧道相对位移时程曲线
3.3.2 盾构法区间与联络通道接口
区间隧道与联络通道存在接口,属于抗震的薄弱
部位,计算时需要考虑额外三维分析,计算模型如图4。
区间隧道与联络通道的结构位移云图,地震作用下X向和Z向位移见图5,其中结构最大位移23.7mm,X向最大位移15.7mm,Z向最大位移17.9mm。从区间结构横断面和纵断面的位移云图可以得知,联络通道处位移并不达到峰值,从结果上判断风险威胁指数较低。
通过计算分析得到,地震作用下,隧道水平方向最大变形差为1.47mm,发生在时间9.44s,隧道顶、底处的最大变形差是0.87mm,发生在9.54s,盾构隧道与联络通道接口部位最大差异变形是17.75mm,发生在10.36s。
地铁区间钢筋混凝土管片材料使用C50混凝土,抗压强度标准值是32.4MPa,抗压设计值是23.1MPa,抗拉强度标准值1.8MPa,抗拉设计标准值是1.44MPa,抗震设计规范要求结构拉、压应力应分别小于1.57MPa和16.7MPa。通过计算分析可以得到,地震作用下,隧道主体峰值拉应力是0.65MPa,隧道与联络通道接口处峰值压应力是0.81MPa。因此,在地震作用下,隧道结构拉应力均小于1.44MPa<1.57MPa,结构构件按照抗拉强度设计值和规范要求分析时符合要求。同理,从压应力计算结果得知隧道主体峰值压应力为8.06MPa,隧道与联络通道接口处峰值压应力为15.9MPa,结构混凝土在地震作用下均小于16.7MPa<23.1MPa,结构从设计标准值和抗震设计规范要求角度分析发现抗拉、压承载力均满足要求,且富余量较大。
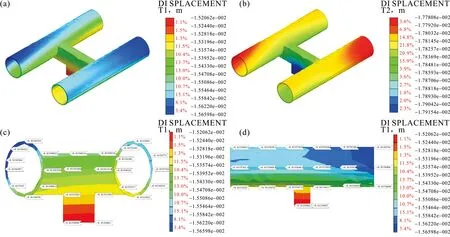
图4 地震作用下区间隧道与联络通道位移云图

图5 相对位移时程曲线
4 结论
本文以西安市某在建地铁某盾构区间主体结构为研究背景,针对地震作用下土体-区间隧道共同作用的地下结构进行抗震动力响应研究。利用粘弹性局部人工边界实现地基开放系统的模拟,边界范围选取时考虑了侧向人工边界的合理性,介质动本构模型采用修正的Davidenkov粘弹性动力本构模型实现有效孔隙水压力和体积应变的变化;混凝土的动力本构关系采取粘塑性动力损伤模型;地震波输入根据场地基岩地震相关反应谱为依据。
通过有限元结构动响应计算,结合超越概率下地震动参数合成的地震动时程对地层、地铁区间顶、底面、侧面、以及联络通道进行具体分析,发现地层和区间隧道均随地震波的输入产生位移变化,且地层位移变化略小于区间隧道,最大响应值均发生在同一时刻,5.5s;区间左、右和顶、底相对位移变化也表现出类似规律,最大响应值产生在9.4s左右。对得到的地层位移时程曲线、地铁区间隧道结构在拱顶、底间的位移差时程、曲线、盾构左、右侧相对位移时程曲线、盾构顶、底面相对位移时程曲线等进行研究发现,X向峰值位移出现在隧道区间中点处,抗震薄弱环节联络通道处位移并不达到位移峰值;混凝土的抗压、抗拉强度通过计算发现均小于结构设计值和规范要求。本文通过地铁区间三维地震动响应分析,结合介质的动本构模型和地震波输入,可以得到位移和内力随地震动时程的变化情况,更具针对性的分析区间结构的最大影响时刻和最不利位置,可辅助类似区间结构的风险抗震分析。
Chen Lei,Chen Guo-xing,Li Li-mei.2001.Seismic response characteristics of the double-layer vertical overlapping metro tunnels under near-field and far-field ground motions[J].China Railway Science,31(1):79-86( in Chinese with English abstract)
Deeks A.J,Mark F.R.1994.Axisymmetric time-domain transmitting boundaries[J].Journal of Engineering Mechanics,120(1):25-42
Gong Bi-ning,Zhao Da-peng.2002.Experimental research on dynamic interaction of underground structure and soil[J].Underground Space,22(4):320-324(in Chinese with English abstract)
Gu Yin,Liu Jing-bo,Du Yi-xin.2007.3D Consistent viscous-spring artificial boundary and viscous-spring boundary element[J].Engineering Mechanics,24(12):31-37(in Chinese with English abstract)
Guo Sheng-bing,Zhao Yi,Zhao Yue-tang.2002.Dynamic analysis of underground structures under the vertical and horizontal seismic load[J].Underground Space,22(4):314-319(in Chinese with English abstract)
Huo H.B,Bobet A.2003.Seismic design of cut and cover rectangular tunnelse-valuation of observed behavior of dakai station during Kobe Earthquake,1995[A].Proceedings of 1st World Forum of Chinese Scholars in Geotechnical Engineering,August 20-22[C].Tongji University,Shanghai:456-466
Jeeho Lee.1998.Plastic-damage model for cyclic loading of concrete structures[J].Journal of Engineering Mechanics,19(4):892-900
Choi J.S,Lee J.S,Kim J.M.2002.Nonlinear earthquake response analysis of 2-D underground structures with soil-structure interaction including separation and sliding at interface[A].15th ASCE Engineering Mechanics Conference,June2-5[C].New York:Columbia University:1-8
Kuang Zhi-ping,Liu Zhu-zhao,Cao Guo-an.2002.Axial random seismic response and external value analysis of underground structures[J].Journal of Tongji University(Natural Science),30( 8):922-926(in Chinese with English abstract)
Liu Jing-bo,Du Yi-xin,Du Xiu-li,Wang Zhen-yu,Wu Jun.2006.3D viscous-spring artificial boundary in time domain[J].Earthquake Engineering & Engineering Vibration,5(1):93-102
Liu Jing-bo,Lü Yan-dong.1998.A direct method for analysis of dynamic soil-structure interaction[J].China Civil Engineering Journal,31(3):55-64(in Chinese with English abstract)
Lin Jing-bo,Gu Yin,Du Yi-xin.2006.Consistent viscous-spring artificial boundary and viscous-spring boundary element[J].Chinese Journal of Geotechnical Engineering,28(9):1070-1075(in Chinese with English abstract)
Rittirong A,Shang J.Q.2008.Numerical analysis for electro-osmotic consolidation in two-dimensional electric field[A].The Proceedings of the Eighteenth International Offshore and Polar Engineering Conference,July 6-11[C].International Society of Offshore and Polar Engineers,Canada Vancouver:566-572
Uenishi K,Sakurai S.2000.Characteristic of the vertical seismic waves associated with the 1995 Hyogo-ken Nanbu(Kobe),Japan earthquake estimated from the failure of the Daikai Underground Station[J].Earthquake Engineering & Structural Dynamics,29(6):813-821
Xie Yun-yue,Xiao Hong-tian,Yan Qiang-gang.2015.Two-Dimensional Numerical Simulation of Macro-Mechanical Parameters for Fractured Rock Mass[J].Geology and Exploration,51(2):376-382(in Chinese with English abstract)
Yuan Guang-xiang,Li Jian-yong,Huang Zhi-quan,Wang Peng-jiao.2015.On Prediction of Water Inflow into Tunnels during Engineering Surveys[J].Geology and Exploration,51(5):993-998(in Chinese with English abstract)
Y.Horibe,H.Yagi,S.Okayasu,T.Ukawa.1995.Connection between two tunnels under a busy crossing in a big city[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,32(3):11-16
Yang Lin-de.2003.Shaking table test on metro station structures in soft soil[J].Modern Tunnelling Technology,40(1):7-11(in Chinese with English abstract)
[附中文参考文献]
陈 磊,陈国兴,李丽梅.2001.近场和远场地震动作用下双层竖向重叠地铁隧道地震反应特性[J].中国铁道科学,31(1):79-86
宫必宁,赵大鹏.2002.地下结构与土动力相互作用试验研究[J].地下空间,22(4):320-324
谷 音,刘晶波,杜义欣.2007.三维一致粘弹性人工边界及等效粘弹性边界单元[J].工程力学,24(12):31-37
国胜兵,赵 毅,赵跃堂.2002.地下结构在竖向和水平地震荷载作用下的动力分析[J].地下空间,22(4):314-319
匡志平,刘竹钊,曹国安.2002.地下结构纵向随机地震响应和极值分析[J].同济大学学报(自然科学版),(8):922-926
刘晶波,吕彦东.1998.结构-地基动力相互作用问题分析的一种直接方法[J].土木工程学报,31(3):55-64
刘晶波,谷 音,杜义欣.2006.一致粘弹性人工边界及粘弹性边界单元[J].岩土工程学报,28(9):1070-1075
谢云跃,肖洪天,闫强刚.2015.裂隙岩体宏观力学参数的二维数值模拟[J].地质与勘探,51(2):376-382
袁广祥,李建勇,黄志全,王朋娇.2015.隧道工程勘察阶段涌水预测的问题探讨[J].地质与勘探,51(5):993-998
杨林德.2003.软土地铁车站结构的振动台模型试验[J].现代隧道技术,40(1):7-11
Three-Dimensional Seismic Response Analysis of a Shield-Shaped Subway Tunnel
BI Ran1,TANG Xiao2,LIU Bao-jian1
(1.RoadandRailwayEngineering,HighwayCollegeofChang’anUniversity,Xi’an,Shaanxi710064;2.CCCCFirstHighwayConsultantsCo.Ltd,RoadandRailwayBranch,Xi’an,Shaanxi710075)
Subways has become an important part of the urban underground transportation networks as well as underground space structure.In order to forecast and reduce the impact of earthquake hazard,using a subway shield-shaped tunnel as an example,this work establishes a three-dimensional calculation model to analyze seismic response.In the calculation,a viscoelastic artificial boundary is employed to simulate the half infinite feature of the foundation.Several earthquake ground motion parameters under different exceeding probability levels are adopted for reference.Considering the random phase affects to fit the seismic ground motion time history samples,a three-dimensional finite element modeling for soil-structure interaction is carried out.The results show that the deformation amounts of the top,bottom,sides and the connecting passage are all deformed caused by the earthquake are all within the allowed range of the relevant codes .The displacement time history curves and tensile and compressive stress distributions clearly show the performance of the subway tunnel anti-earthquake structure.The most vulnerable position is the connecting passage,but its inner stress and deformation still satisfies the safety requirement of the codes.
subway tunnel,underground space structure,seismic resistance,three- dimensional analysis model,seismic response,time history analysis
2016-01-06;
2016-06-12;[责任编辑]陈伟军。
国家留学基金联合培养项目(201306560005)资助。
毕 冉(1988年-),女,博士研究生,主要研究方向为岩土工程。E-mail:cs_biran@sina.com。
U231
A
0495-5331(2016)04-0712-06
Bi Ran,Tang Xiao,Liu Bao-jian.Three-dimensional seismic response analysis of a shield-shaped subway tunnel[J].Geology and Exploration,2016,52(4):0712-0717.

