灰色Verhulst-BP模型在沉降分析中的应用

高良博，贾 伟

（1.辽宁科技大学，辽宁 鞍山 114051；2.中交四航工程研究院有限公司，广东 广州 510220 ）

灰色Verhulst-BP模型在沉降分析中的应用

高良博1，贾 伟2

（1.辽宁科技大学，辽宁 鞍山 114051；2.中交四航工程研究院有限公司，广东 广州 510220 ）

针对软基处理后的地基沉降情况进行分析，利用灰色Verhulst-BP模型对沉降数据进行分析预测。灰色Verhulst-BP模型是利用灰色Verhulst模型的残差值来改进BP神经网络模型，进而提高模型的模拟预测精度。在Matlab9.0平台上，通过Matlab语言编程实现实例检验分析。研究结果表明，灰色Verhulst-BP模型相对于灰色Verhulst模型更适合于S型序列的数据分析预测。该模型预测精度较高，能够较好地反映沉降趋势。

软基；沉降；灰色Verhulst-BP模型；预测分析

软基处理[1]是对于建筑物基础不稳定的情况下进行的加固处理，而对于处理后地基沉降情况的分析尤为重要。地基沉降情况复杂，影响因素既包括已知信息同时也包括未知信息，而针对未知信息的分析，主要利用灰色理论方法[2]。灰色理论主要针对贫信息的情况，由于路基沉降监测不确定因素较多，因而更加适用于灰色理论模型的分析[3]。本文主要采用灰色Verhulst-BP模型，该模型是灰色Verhulst模型对BP神经网络模型的改进，具有较强的灰色分析预测能力[4]。

1 灰色Verhulst-BP模型

1.1 灰色Verhulst模型的建立

灰色Verhulst模型[5]：

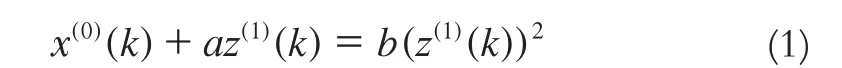
式中，x(0)为原始数据序列，z(1)为x(0)的1—AGo紧邻均值生成序列。

建立白化方程为：

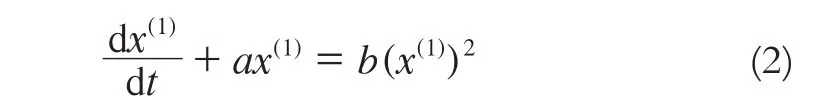
时间响应序列为：

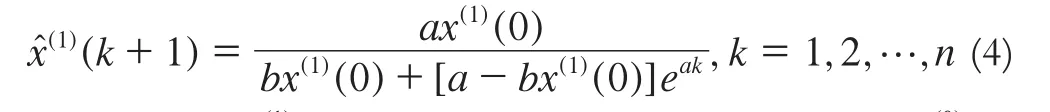
通过对xˆ(1)的模拟值进行IAGo运算还原出x(0)的模拟值：

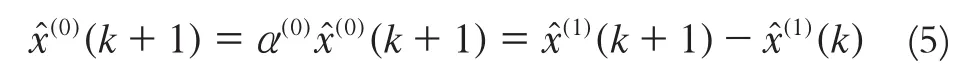
当k≤n时，称xˆ(0)（k）为模型模拟值；当k＞n时，称xˆ(0)（k）为模型预测值。

1.2 灰色Verhulst-BP模型的建立

灰色Verhulst-BP模型是利用灰色Verhulst模型的预测残差值来修正BP神经网络，进而提高BP神经网络模拟预测的精度，为地基沉降分析提供有效的参考信息。

灰色Verhulst-BP模型的建模方法如下：

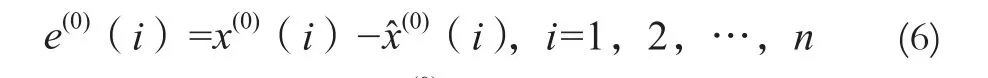
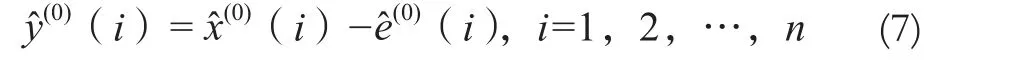
1.3 精度评定

为了有效地评价和衡量模型预测精度，采用如下参考指标来对预测精度进行评价。

1）均方误差（MSE），该指标主要用于评价模型精度的高低，若数据变化程度小，则MSE的值越小，模型精度就越高：

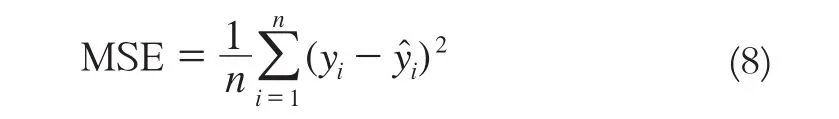
2）平均相对误差（MRE），又称平均绝对偏差：

式中，yi为实际值；yˆi为预测值。

2 实例分析

本文利用灰色Verhulst-BP模型，对某软基处理地基沉降监测点的数据进行分析。

2.1 灰色Verhulst模型的预测分析

设原始数据序列为：

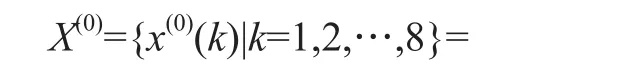
{10.07,12.16,15.58,19.66,23.47,27.25,30.19,31.76}

利用灰色Verhulst模型的Matlab程序对原始数列进行模拟预测，模拟预测结果见表1。

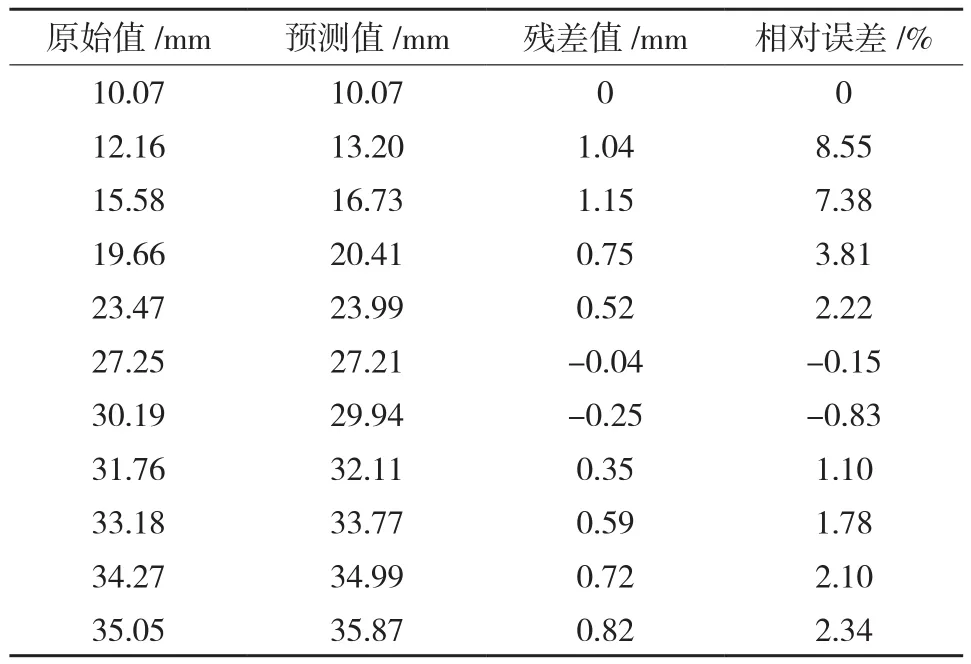
表1 数据序列的预测结果

由表1可得，其MRE为2.57%， MSE为0.45。

2.2 灰色Verhulst-BP模型的预测分析

由表1得残差序列e(0)={0,1.04,1.15,0.75,0.52,-0.04, -0.25,0.35,0.59,0.72,0.82}。

将其分为训练样本和检验样本，6期的训练样本和2期检验样本均以前3个残差值作为输入样本，后一个残差值作为输出样本，形成等维新息样本,如表2所示。

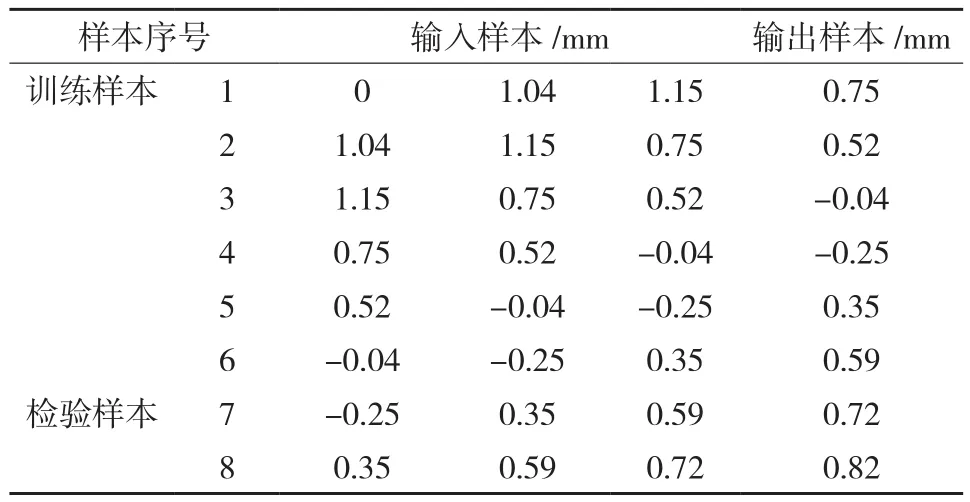
表2 灰色Verhulst-BP神经网络样本选取表

灰色Verhulst-BP模型神经网络训练Matlab程序为：

net=newff(minmax(p),[3,9,1],{ 'tansig','logsig','purelin'},'trainlm'),

net.trainparam.show=100,

net.trainparam.Ir=0.05,

net.trainparam.epochs=100000,

net.trainparam.goal=1e-4,

[net,tr]=train(net,p,t)，

由于隐层神经元的选取需要试算，本文选取9时效果最好，故灰色Verhulst-BP模型神经网络拓扑结构为3-9-1。在训练之前需要将原始数据归一化，设置传递函数如表3所示。

表3 灰色Verhulst-BP模型神经网络拓扑结构

训练函数选取Levenberg-Marquardt算法——trainlm。通过trainlm算法训练得到残差序列的新预测值，进而改进预测值 y ˆ(0)（i），预测结果见表4。

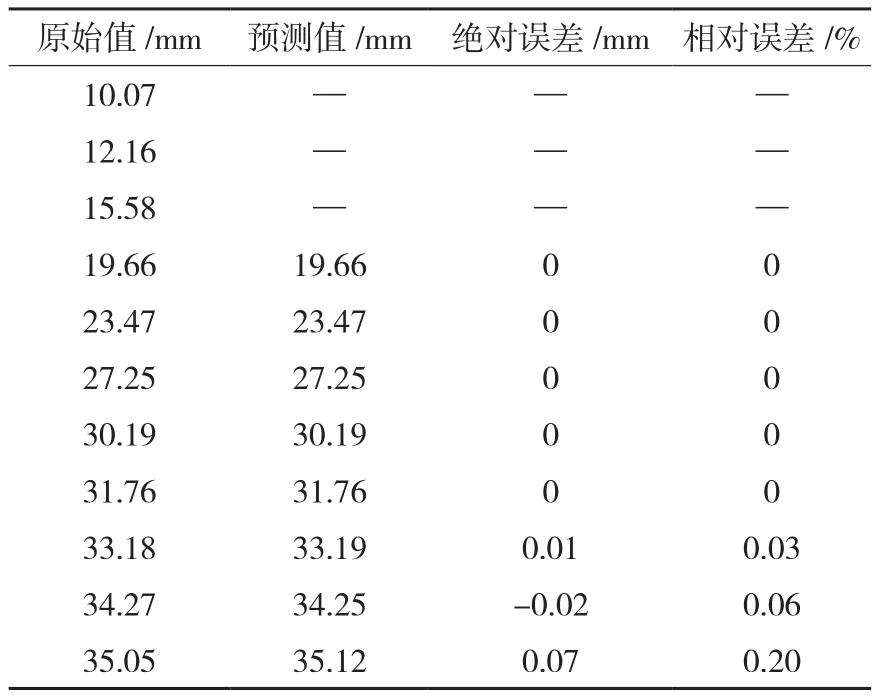
表4 灰色Verhulst-BP模型预测结果表

依据表4可知，其MRE为0.026%，MSE为0.000 5。由于表4中序号4～8项的模型预测绝对误差和相对误差值很小，以mm为单位显示已经无法表达其测量意义，故表示为零值。

为方便比较，现将几种理论模型与灰色Verhulst-BP模型预测的结果进行比较（图1），见表5。

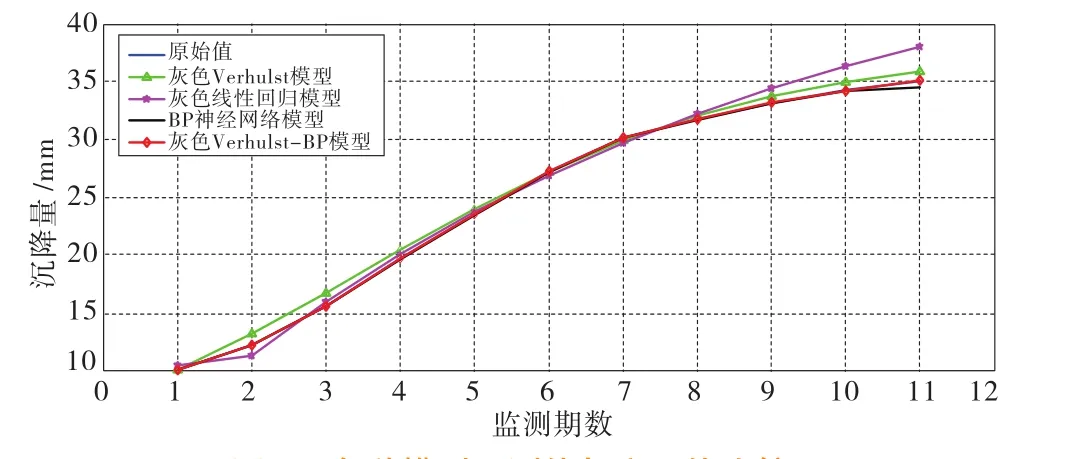
图1 各种模型预测值与实际值比较

由表5和图1可知，与其他3种模型相比，灰色Verhulst-BP模型模拟预测效果更好，如11期预测值相对误差，灰色Verhulst模型、灰色线性回归模型和BP神经网络模型分别为灰色Verhulst-BP模型的11.7倍、42.95倍、7.15倍，而通过MSE和MRE比较则更具说服力（表6）。

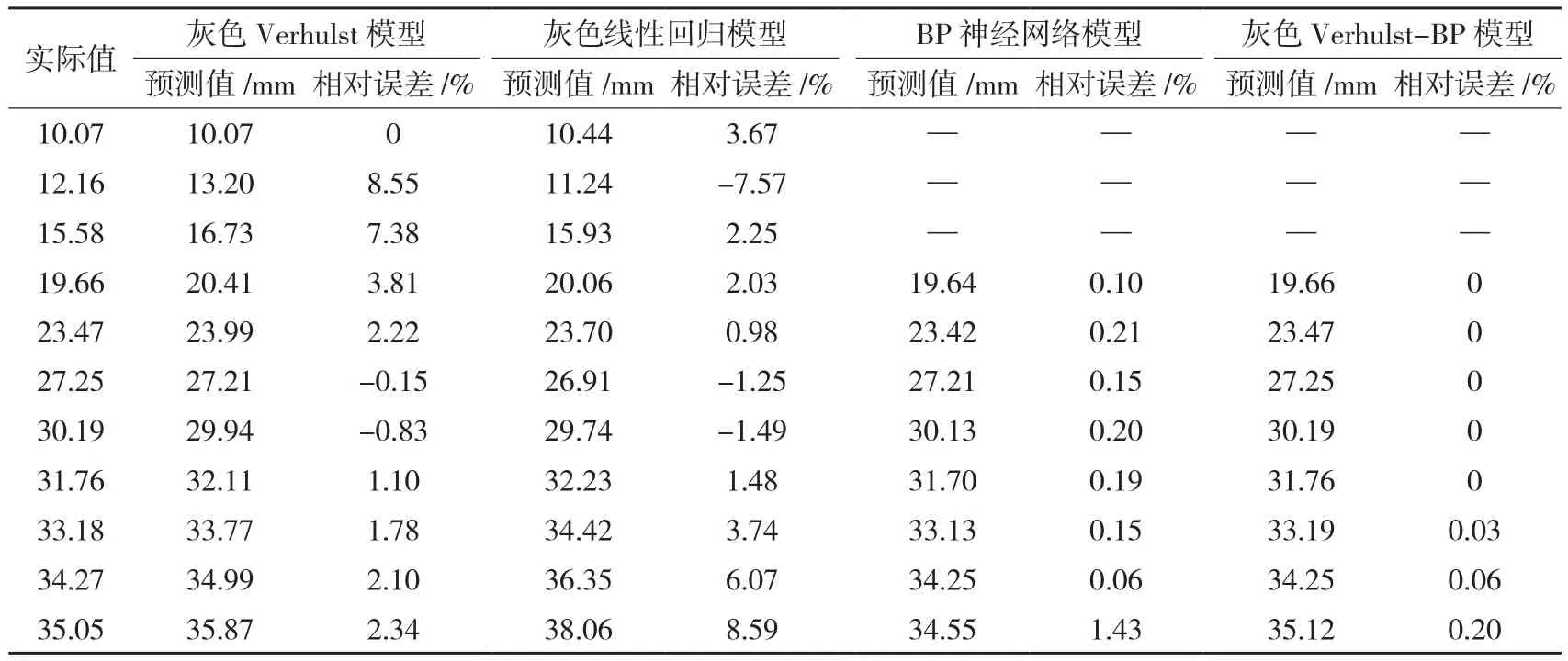
表5 各种模型预测值及误差比较

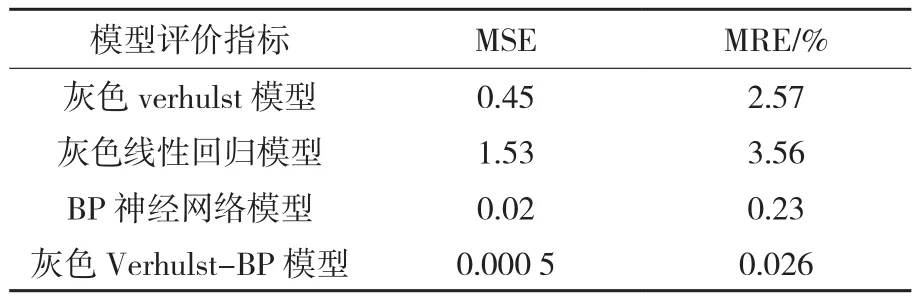
表6 模型预测值误差评价

3 结 语

通过灰色Verhulst-BP模型与其他模型预测结果进行对比，得到以下结论：

1）针对于S型序列的数据，灰色Verhulst-BP模型的模拟预测效果更好，从其相对误差来看也符合预测分析的规律。

2）由表5灰色Verhulst-BP模型的9～11期预测相对误差可知，随着预测期数的增加，预测精度随之降低，但相对其他模型仍能保证较好的预测精度。

3）灰色Verhulst-BP模型是基于灰色Verhulst的改进，因此灰色Verhulst模型的预测效果直接影响到灰色Verhulst-BP模型的预测精度和效果，同时BP神经网络算法的选取也直接影响着模型运算的效率及预测效果。

[1] 郭策,王立峰,陈小乐,等.软基沉降监测及处理技术研究[J].黑龙江交通科技,2014(2)：73-74

[2] 邓聚龙.灰理论基础[M].武汉：华中科技大学出版社,2002

[3] 刘峰.基于灰色Verhulst模型对边坡变形预测研究[J].公路工程,2013(4)：265-268

[4] 米鸿燕,蒋兴华.基于灰色BP神经网络的沉降预测模型应用研究[J].昆明理工大学学报(理工版),2007(2)：65-68

[5] 周德强,冯建中.建筑物沉降预测的改进Verhulst模型研究[J].地下空间与工程学报,2011(1)：194-198

[6] 王婷婷,靳奉祥.基于BP神经网络法的地表变形监测[J].测绘与空间地理信息,2014(3)：57-61

[7] 刘国仕,何亮云,薛建华,等.灰色线性回归组合模型在沉降监测中的应用[J].长沙理工大学学报(自然科学版),2012(4)：32-36

[8] 陈正威,王铁生.Verhulst模型在深基坑坑周土体水平位移预测中的应用[J].华北水利水电学院学报,2014(1)：42-45

[9] 胡志刚,花向红. Levenberg-Marquarat算法及其在测量模型参数估计中的应用[J].测绘工程,2008(4)：31-34

P258

B

1672-4623（2016）08-0090-03

10.3969/j.issn.1672-4623.2016.08.030

高良博，硕士研究生，主要研究方向为测绘信息采集及处理。

2014-09-23。