基于改进残差重采样粒子滤波的纯方位目标追踪

杨伟明，薛 召，刘玉良

(天津科技大学电子信息与自动化学院，天津 300222)

基于改进残差重采样粒子滤波的纯方位目标追踪

杨伟明，薛 召，刘玉良

(天津科技大学电子信息与自动化学院，天津 300222)

目标被动追踪利用持续的观测信息来估计目标的运动状态，针对此问题提出了一种改进残差重采样粒子滤波算法．算法考虑采样粒子集的空间分布特性，将粒子集空间分布分割为数量可变、可数的网格，在每个网格内运用时间序列相关性分析选择重要粒子，能够丰富采样粒子的多样性，并将该网格内所有粒子的残余权值和赋予该重要粒子，从而削弱采样粒子的退化现象，提高非线性系统状态估计精度．实验表明：当观察噪声方差小于系统噪声方差，特别是当初始采样粒子数目较小时，该算法在单站纯方位目标追踪状态估计中的精度优于传统残差重采样粒子滤波算法．

粒子滤波；纯方位目标追踪；残差重采样

目标追踪利用雷达、红外以及可见光等传感器的测量数据对目标的状态进行估计，正日益广泛地应用于科学技术、国防建设以及国民经济的各个领域[1]．从信息获取方式上通常分为主动追踪和被动追踪.随着反跟踪技术的不断完善，主动追踪利用目标反射的回波进行探测，容易暴露自身而遭到对方的攻击．而被动追踪利用持续的观测信息来估计目标的运动状态，可以很好地克服这一缺点．目标被动追踪理论和实际应用一直都是人们广泛研究的一个重要课题，其中纯方位目标追踪[2-3]问题更因其固有的优势而成为当前研究的热点．该课题研究一个在二维空间中移动目标的追踪问题，在固定的间隔时间内利用传感器观测目标的方位(角度)，而不是测量与目标间的距离，仅仅利用观测到的方位信息来估计运动目标的状态．

利用角度测量估计目标的位置和速度实质上是一个非线性状态估计问题．1960年，Kalman[4]提出了经典的卡尔曼滤波器(Kalman filter，KF)，为线性高斯系统状态估计提供了一种最优的解决方法．然而在现实世界中，实际问题大都具有非线性非高斯特征，解决非线性非高斯系统状态估计的传统方法是扩展卡尔曼滤波算法(extended Kalman filter，EKF)[5]和无极卡尔曼滤波算法(unscented Kalman filter，UKF)[6]．它们以EKF框架为基础，对非线性系统的后验概率密度作高斯假设，因此不适应一般的非高斯分布模型．

解决非线性系统状态估计问题的另一种方法为序贯重要性采样算法(sequential importance sampling，SIS)[7-10]，也称为粒子滤波算法(particle filter，PF)．由于该方法存在严重的样本权重退化问题，因此直到1993年，Gordon等[11]才将重采样步骤(resampleing)引入粒子滤波过程，提出一种自举滤波器，有效地解决了粒子权重退化现象，称为序贯重要性重采样粒子滤波算法(sequential importance resampling，SIR)．但同时带来另外一个难题：粒子贫化，少数粒子拥有重要的权重，而大多数粒子由于较小的权重在重采样过程中被丢弃．特别当系统状态噪声方差较小时，重采样后的粒子集集中在一个较小的区域中，导致较大的系统状态估计误差．

截至目前，大多数SIR算法在重采样[12-14](多维重采样、系统重采样、残差重采样、分层重采样等)步骤中只关注采样粒子的权重，而忽略了它们的空间分布，譬如粒子状态值．基于权重的重采样步骤中任意的去除权值小的粒子，仅复制权重大的粒子，导致经过重采样步骤后的状态概率分布与原概率分布有较大的偏差．

本文提出一种改进的残差重采样算法，在重采样步骤中不仅考虑采样粒子的权值，而且考虑粒子的空间分布信息[15]，引入时间序列相关性分析[16]作为重要粒子选择的依据进行重采样，并进行了仿真实验．

1 序贯重要性重采样粒子滤波算法

在贝叶斯公式推理中，PF采用一组从建议分布中采样带有权值的样本(或称粒子)、权值，且满足的集合，Nt为采样粒子数．根据这一支持样本(粒子)集近似表示系统状态的后验概率分布f( xt|y1:t)．

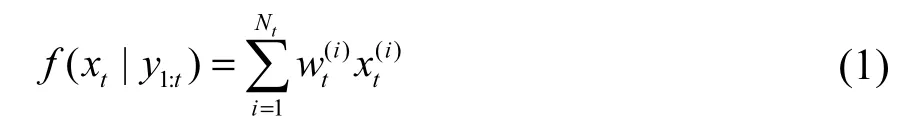
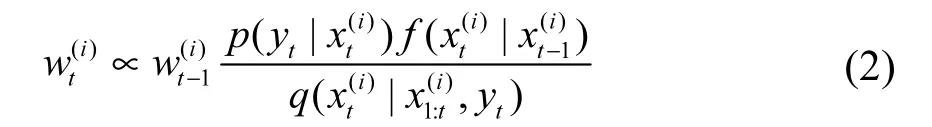
在粒子传播过程中经过少数的迭代步骤，将产生粒子权值退化现象，仅有少数的粒子拥有重要的权值，大多数粒子的权值几乎可忽略不计．为了解决粒子退化问题，在SIS中引入式(3)重采样步骤[11]，删除权值小的粒子，复制权值大的粒子．

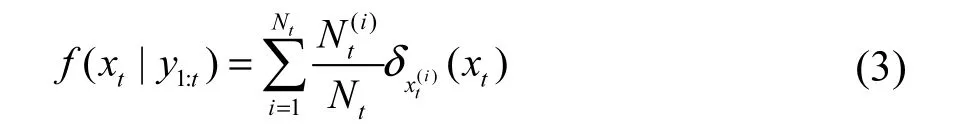
重采样过程在粒子滤波过程中重新设置采样粒子分布，能够减小在SIS中系统状态估计急剧增加的方差，残差重采样过程见图1．

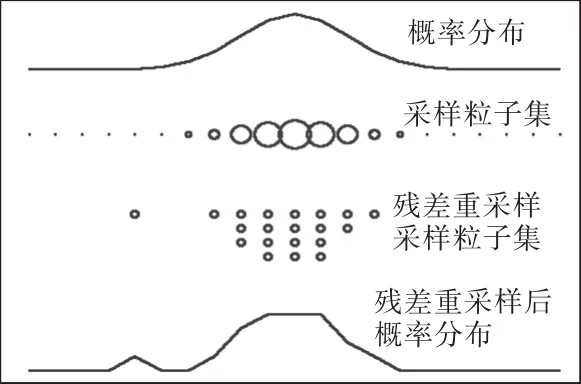
图1 残差重采样过程Fig. 1 Procedure of residual resampling

在重采样步骤中，残差重采样只考虑了粒子的权值，仅复制大权值的粒子，丢弃小权值的粒子，经过几次重采样步骤后，导致采样粒子集中在一个小的重要区域中，降低了粒子的多样性，为系统状态估计带来较大的估计误差．

2 改进残差重采样粒子滤波算法

改进算法是基于残差重采样[14]，在残差重采样算法的第二步中将粒子空间分布分割为数量可变、可数的区域(网格)．依据系统状态转移函数将采样粒子转移至状态空间的任意区域，因此粒子的空间分布表示了采样粒子的多样性与系统状态估计的不确定性．所以，网格数量的一个重要功能就是定义了采样粒子集的多样性与系统状态估计的不确定性．

2.1 基于采样粒子状态将粒子空间分割

计算采样粒子集在空间分布上各维的最大值、最小值，然后将最大值、最小值区间按照设定的长度L进行分割．一个粒子只能属于一个网格，每个网格都是独立的，在每个网格中运用时间序列相关性分析选择重要粒子，能够在不增加初始采样粒子数量的前提下提高粒子的多样性，并将该网格内所有粒子的权值赋予该重要粒子，削弱了粒子滤波的退化现象，从而提高系统状态估计精度．初始长度参数L和采样粒子集空间分布的分散程度决定了网格分割的数量，粒子集越分散，网格数越多，采样粒子的多样性程度越高，反之越少．一般来说，L的选择依赖于期望的采样粒子数，而且应根据粒子滤波器的具体应用考虑计算量和状态估计精度进行调整．为了在2.3节算法步骤中描述方便，定义

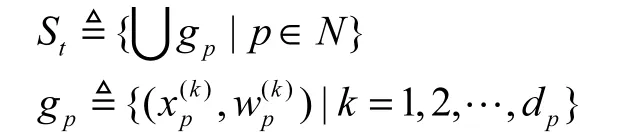
式中：St为t时刻粒子集的空间分布；gp为整个粒子空间分割成的网格；下标p表示第p个网格；dp表示第p个网格中粒子的数量．

2.2 采用时间序列相关性选择重要粒子

肯德尔相关系数[16]可以用于度量两个时间序列的相关性．在2.1节分割的每个独立的网格中，运用肯德尔时间序列相关系数度量各粒子观测路径和系统观测路径的相关性，显而易见，选择接近系统状态程度较高的粒子将在系统状态估计中起到比较重要的作用，所以选取线性相关程度最高的粒子作为该网格的重要粒子．

2.3 改进残差重采样粒子滤波算法步骤

如前所述，应用粒子滤波器解决非线性系统状态估计时，在重采样中保留重要粒子缓解粒子贫化现象是必须的．本文在残差重采样过程中引入重要粒子选择过程，以提高采样粒子的多样性，具体算法步骤如下：

(1)改进的粒子滤波重采样算法的第一步和残差重采样相同，复制粒子．

首先将所有采样粒子的权值乘以采样粒子数Nt；然后将每个粒子复制次，并赋予相同的权值(权值的大小在步骤(4)中定义)，其中取小于最大的整数值；再将减去得到所有粒子残余的权值

(2)将采样粒子集分割成数量可变、可数的网格．

(3)在每个网格中使用肯德尔相关系数选择重要粒子，过程为

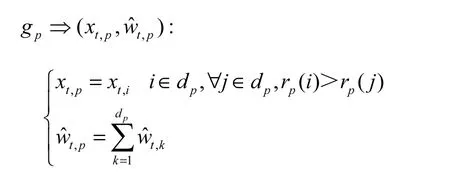
改进残差重采样过程见图2．

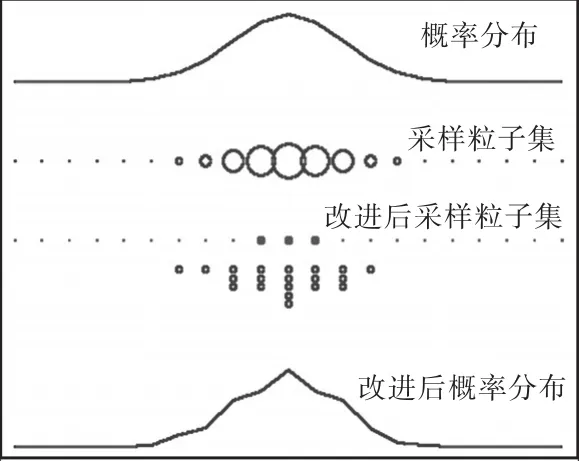
图2 改进残差重采样过程Fig. 2 Procedure of improved residual resampling

在图2中可以看到，改进残差重采样过程采样粒子集不仅包含了大权重粒子而且还保留了小权重的粒子，表明改进残差重采样算法提高了采样粒子集的多样性，减弱了采样粒子的退化现象．图2与图1进行比较，经过改进残差重采样粒子滤波算法计算得到的近似概率分布比残差重采样粒子滤波算法计算得到的近似概率分布更接近重采样前的概率分布．

计算复杂度指对总运算次数表达式中影响最大的项(不含系数)，所以改进残差重采样粒子滤波算法的计算复杂度为O( Nt)，Nt为重采样的粒子数．从计算过程可以看到，步骤(1)、(2)和(4)中复制粒子、粒子状态空间分割和粒子赋值的计算复杂度为O( Nt)，步骤(3)中重要粒子选择的计算复杂度为O( M)，M为重要粒子个数，且满足M＜Nt，只是在步骤(3)中多了一些时间序列相关性的计算．所以该重采样粒子滤波算法的计算复杂度为O( Nt)．

3 仿真实验

3.1 仿真模型

式(5)表示一个二维空间中单站纯方位目标运动的数学模型．

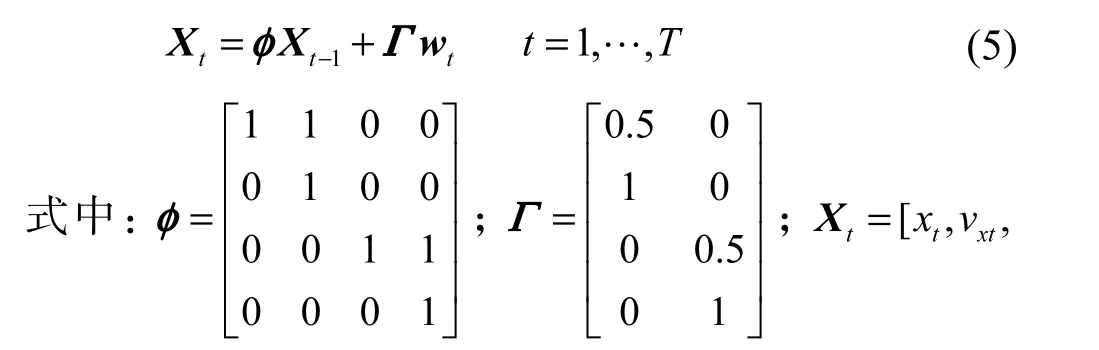
应用式(6)观测方程对式(5)系统运动方程的仿真数据生成观测数据进行仿真实验．

式中：zt为观测数据；vt为观测过程零均值高斯白噪声，vt～N()．

参照文献[11]设置初始化参数．其中X0=[−0.05, 0.001,0.7,−0.055]T，σw=0.001，σv=0.005，μ0=

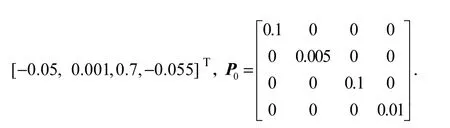
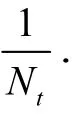
采用均方根误差(root mean square error，RMSE)评估非线性系统的状态估计精度：

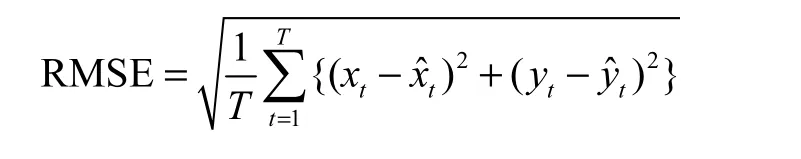
式中：xt、yt、、分别为系统状态t时刻在x、y方向的真实值和估计值；T为仿真时间步数．

3.2 结果与讨论

按照上述设计，设置仿真步数T=25，初始粒子数为100，进行仿真，仿真结果见图3，残差重采样与改进残差重采样路径估计的均方根误差分别为0.444,3、0.069,0．

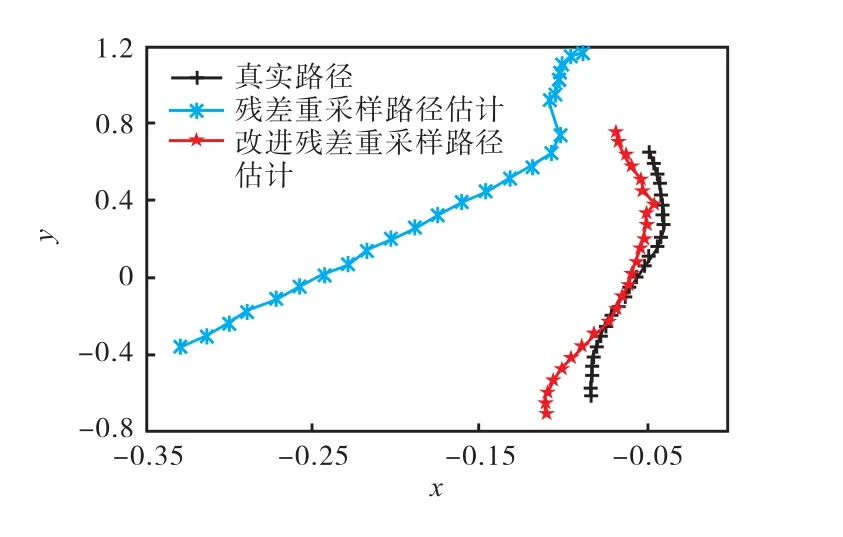
图3 随机仿真实验结果Fig. 3 Result of a random simulation

在相同的仿真环境下仿真10次，记录均方根误差，结果见图4．从图3和图4中可以看到，改进的残差重采样算法比残差重采样算法的估计值更接近真实值．

最后采用从10到100(间隔10)作为每次仿真的起始粒子数，仿真10次，记录在不同初始粒子数仿真的均方根误差，仿真结果见图5．从图5中可以观察到，当初始粒子数较小时(特别是在粒子数＜50时)，改进的重采样算法性能表现更优越．这是因为改进的重采样算法采用粒子空间分割、使用时间序列相关系数选择网格中的重要粒子，从而提高了粒子的多样性，降低了粒子退化现象，提高了系统状态的估计精度．

4 结 语

本文提出了一种改进重采样的粒子滤波算法，在重采样步骤中考虑采样粒子集的空间分布特性，引入时间序列分析选择重要粒子，丰富了采样粒子集的多样性，削弱了采样粒子的贫化现象，进而使系统状态的估计精度得到了提高．仿真结果表明，改进的重采样粒子滤波算法在单站纯方位目标追踪状态估计中优于传统的重采样粒子滤波算法，尤其针对初始粒子数目较小的情况，改进效果更加明显．

［1］ 高文，朱明，贺柏根，等. 目标跟踪技术综述[J]. 中国光学，2014，7(3)：365-375.

［2］ 任波，闫向远. 纯角度跟踪非线性预测滤波算法研究[J]. 弹箭与制导学报，2014，34(2)：6-8.

［3］ 梁军，彭喜元. 基于观测相似性粒子滤波的纯角度目标跟踪[J]. 电子测量与仪器学报，2009，23(2)：10-14.

［4］ Kalman R E. A new approach to linear filtering and prediction problem[J]. Transactions of the ASME：Journal of Basic Engineering，1960，82(1)：35-45.

［5］ Daum F. Nonlinear filters：Beyond the Kalman filter[J]. IEEE Aerospace and Electronic Systems Magazine，2005，20(8)：57-69.

［6］ Julier S J，Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE，2004，92(3)：401-422.

［7］ Cappé O，Godsill S J，Moulines E. An overview of existing methods and recent advances in sequential Monte Carlo[J]. Proceedings of the IEEE，2007，95(5)：899-924.

［8］ 王法胜，鲁明羽，赵清杰，等. 粒子滤波算法[J]. 计算机学报，2014，37(8)：1679-1694.

［9］ Djuric P M，Kotecha J H，Zhang J Q，et al. Particle filtering[J]. IEEE Signal Processing Magazine，2003，20(5)：19-38.

［10］ Johansen A M，Doucet A. A note on auxiliary particle filtering[J]. Statistics & Probability Letters，2008，78(12)：1498-1504.

［11］ Gordon N J，Salmond D J，Smith A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. Radar & Signal Processing IEE Proceedings F，1993，140(2)：107-113.

［12］ 冯驰，王萌，汲清波. 粒子滤波器重采样算法的分析与比较[J]. 系统仿真学报，2009，21(4)：1101-1105.

［13］ Li T C，Bolic M，Djuric P M. Resampling methods for particle filtering：Classification，implementation，and strategies[J]. IEEE Signal Processing Magazine，2015，32(3)：70-86.

［14］ Liu J S，Chen R，Logvinenko T. A Theoretical Framework for Sequential Importance Sampling with Resampling[M]. New York：Springer-Verlag，2001.

［15］ Li T C，Sattar T P，Sun S D. Deterministic resampling：Unbiased sampling to avoid sample impoverishment in particle filters[J]. Signal Processing，2012，92(7)：1637-1645.

［16］ 徐维超. 相关系数研究综述[J]. 广东工业大学学报，2012，29(3)：12-17.

责任编辑：常涛

Bearing-only Target Tracking with an Improved Residual Resampling Particle Filter

YANG Weiming，XUE Zhao，LIU Yuliang
(College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China)

Problems in single station passive target tracking for estimating the state of the moving target based on successive measurement have been studied．Based on this，an improved residual resampling particle filter algorithm was proposed，which prevents uncensored discarding of the low weighted particles and maintains the diversity of the sample particles．The key idea in the new algorithm is to select the important particles based on not only their weight but also their state values．Simulations of single station passive target tracking demonstrate the estimation accuracy of the algorithm，which is better than the traditional residual resampling method，especially when the sample size is small.

particle filter；bearing-only target tracking；residual resampling

TP391.99

A

1672-6510(2016)06-0074-05

10.13364/j.issn.1672-6510.20150254

2015-12-20；

2016-06-30

国家自然科学基金资助项目(51674176，81472070)；天津市高等学校科技发展基金资助项目(20130707)

杨伟明（1980—），男，山东人，实验师；

刘玉良，副教授，ylliu@tust.edu.cn.