快速网格路径算法在对流层层析中的应用

杨 飞，郭际明，史俊波

（1.武汉大学 测绘学院，湖北 武汉 430079）

快速网格路径算法在对流层层析中的应用

杨 飞1，郭际明1，史俊波1

（1.武汉大学 测绘学院，湖北 武汉 430079）

在GNSS对流层层析应用中，常规的网格辐射路径算法是利用空间平面与空间直线求截距。本文介绍了一种快速求解算法，用于计算网格辐射路径，构造层析系数矩阵。结果表明，快速求解方法与常规方法解算精度相当，当射线条数大于500时，计算效率明显提高。

对流层层析；层析网格；系数矩阵；网格辐射路径

GNSS对流层层析是求解对流层水汽密度，从而反映对流层水汽在三维空间分布情况的方法[1]。对流层层析首先要划分层析网格，建立层析观测方程[2]，求解层析方程系数矩阵，该系数是每条GNSS射线穿过的层析网格内的截距，精确的对流层层析网格辐射路径算法是层析计算的关键。陈宏斌[3]提出了利用空间直线与空间平面的关系求解算法；胡金玉[4]提出了利用卫星信号路径与纬度面、经度面、高度面联合求解算法。这些都属于常规的逐个平面解算方法，没有详尽阐述解算过程。在放射性治疗应用中，Siddon[5]提出了一种三维CT数组辐射路径的快速算法。本文将医学CT中的算法用于GNSS对流层层析网格辐射路径的解算，利用已知测站坐标和卫星坐标求解各段路径在总路径中的比例关系，可以得到与常规方法相同精度的结果，提高解算效率。

1 三维层析网格系数矩阵常规方法

层析观测方程[6]如式（1）所示：

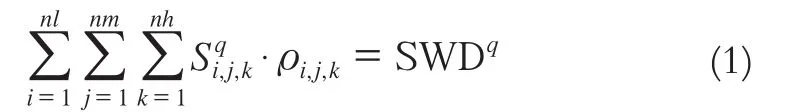
式中，nl、nm、nh分别为经度、纬度和高程方向划分的网格数量；Sqi,j,k为第q条卫星信号穿过（i，j，k）网格单元的路径长度；ρi,j,k为相应立体网格的水汽密度；SWDq为第q条卫星信号倾斜路径延迟[7]。将式（2）写成矩阵形式：

式中，SWD是n×l阶倾斜路径湿延迟向量，x为m×l阶未知参数向量。A为n×m阶层析系数矩阵，其第j行第i列的元素表示第j条射线穿过网格i的长度[8]。所以构建层析观测方程解算层析结果，需要进行层析网格辐射路径长度的求解。

对流层层析常采用逐个平面求解的方法。如图1所示，将卫星信号射线AB视为空间直线，将经度、纬度、高程面视为空间平面，依次求空间直线AB与各个空间平面交点P1、P2、P3，分别得到线段P1P2、P2P3的长度及其所在网格的位置。

图1 卫星信号射线穿过层析网格示意图

2 层析网格辐射路径快速求解算法

快速求解算法将第一个交点P1作为起点，通过递归循环得到其他所有交点，并求出每个格网路径长度具体步骤如下：

1）点线面的初始化。将地面测站点A与卫星位置点B的信号简化为射线AB，利用式（3）参数化，参数α在A点时为0，在B点时为1；将层析区域划分为（Nx-1，Ny-1，Nz-1）个网格单元，利用式（4）将经度、纬度和高程面参数化：

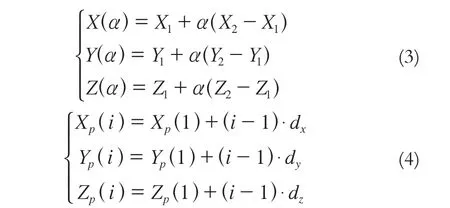
式中，X1、Y1、Z1表示点A的三维坐标；Xp（i）、Yp（i）、Zp（i）表示网格化后的各个经度面、纬度面、高程面；dx、dy、dz分别表示经度方向、纬度方向和高程方向相邻两个平面间的距离。

2）求取参数集合{α}，即各个穿刺点在整条卫星信号中的比例因子。首先，利用上述参数化点面计算类似求取αy（i）、αz（i）；接着，利用式（5）由上述参数值求取αmin和αmax：

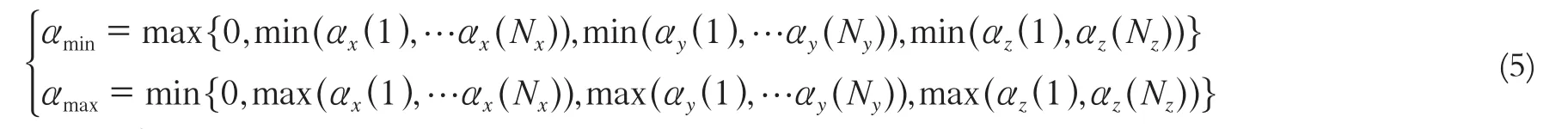
然后，利用式（6）求解参数集合{αx}、{αy}、{αz}：

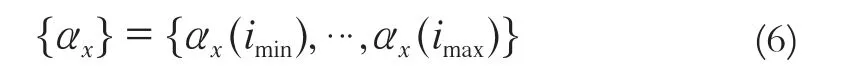
其中需要利用式（7）得到（imin，imax）、（jmin，jmax）、（kmin，kmax）：

利用类似公式求取相应y、z和j、k参数。最后，利用式（8）得到参数集合{α}：

3）利用上述参数集合求取射线与三维网格的交点距离Sqi,j,k。设m和m-1为射线与一个网格的两个交点，则存在如下关系：

4）确定网格[i（m），j（m），k（m）]在全体三维网格中的位置，与网格交点m和m-1有下列关系式：

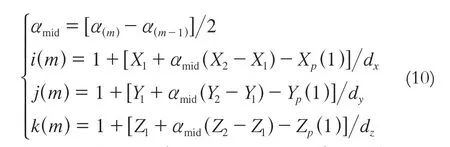
5）经过4）的计算，得到卫星信号穿过层析网格的位置（i，j，k）及长度构成层析方程系数矩阵[10]。

3 实验验证

为验证快速算法的准确性和效率，以武汉CORS网络进行层析建模。经度范围是113.8°～115.0°，纬度范围是30.0°～31.0°，高度范围是0～10 km。首先，选取测站WHHN和WHXZ于 2013-05-06的GPS观测数据，计算卫星相对于测站的高度角和方位角。然后，划分层析网格，水平分辨率设为0．2°，垂直分辨率设为500 m，共6×5×20个网格，如图2所示。最后，分别选取两个测站的500条卫星信号进行层析网格辐射路径求解，比较2种方法的解算精度。

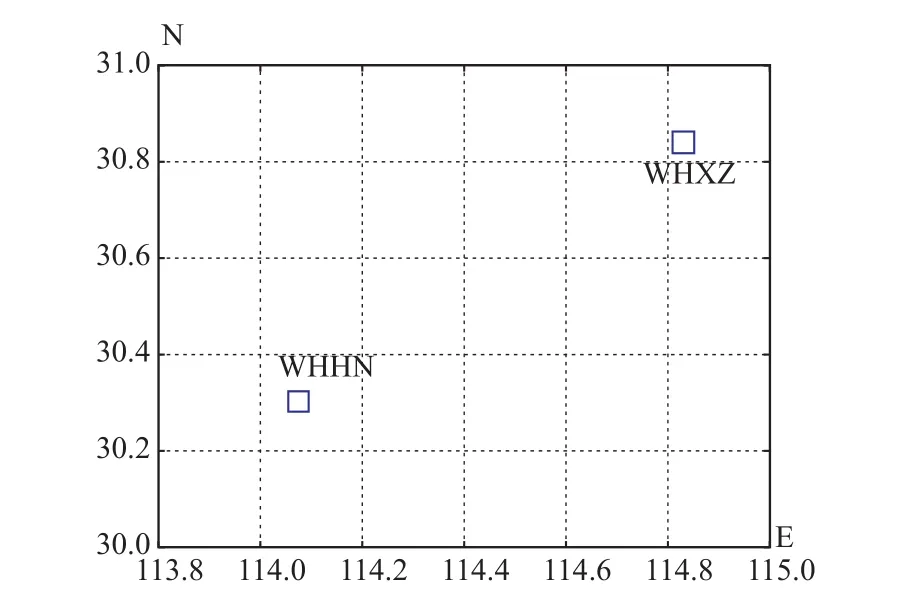
图2 地面层析网格划分及测站位置图

3.1 精度验证

本次层析实验中，测站WHHN和WHXZ的500 条卫星信号分别穿过网格单元的次数为10 520次和10 451次。其中，一条卫星信号最多穿过24个网格单元，最少穿过20个网格单元。以常规方法解算结果作为参考，计算快速解算方法中各测站不同数量卫星信号射线穿过层析网格的平均误差和RMS，如图3所示。

图3 快速解算法与常规解算方法的平均误差和RMS

快速求解算法的平均误差随着卫星信号射线数量的增加而趋于稳定，测站WHXZ稳定于0．248 m（图3a），测站WHHN稳定于0．232 m（图3b）。另一方面，两个测站的RMS也随着卫星信号射线数量的增加而趋于稳定，其稳定值分别为0．417 m（图3c）和0．371 m（图3d）。实验结果说明，快速解算方法与常规解算方法结果差值的平均误差在25 cm左右，RMS在40 cm左右。相对于格网长度（≥500 m），平均误差比例小于等于0．05%， RMS不超过0．08%，可以用于构建层析系数矩阵。

3.2 快速求解算法的效率验证

为了验证快速算法的效率，选取不同数量的射线进行层析网格求解，统计解算时间，每种情况进行10 次计算取平均时间，结果如图4所示。

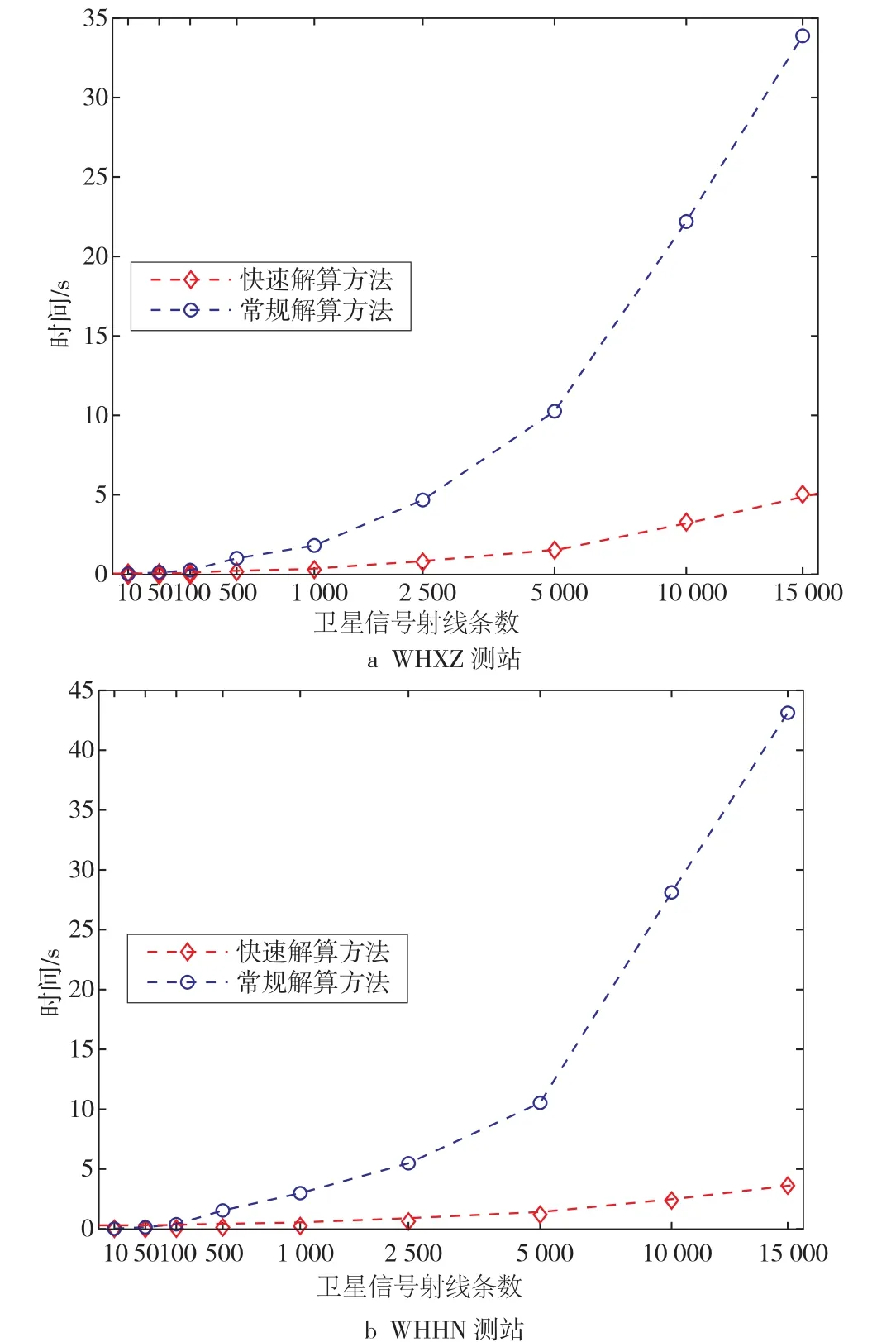
图4 两种方法解算时间对比图

从图4可以看出，无论卫星信号射线条数的多少（0～15 000），快速解算方法所用时间都小于常规解算方法。当射线条数小于500时，时间效率的差别不明显。以WHHN测站为例，当射线条数为500时，两种方法解算时间都小于2 s，分别为1．545 s和0．125 s，快速解算法比常规解算法快1．420 s。随着射线条数的逐渐增加，两种方法的效率差别更加明显；当射线为1 000条时，快速解算方法比常规解算法快2．753 s；当射线为15 000条时，快速解算方法比常规解算法快39．518 s。

实验结果表明，在GNSS对流层层析网格解算过程中，无论测站位置和卫星信号数量，尤其在卫星信号数量大时，快速解算法能提高计算效率。

4 结 语

三维层析网格系数矩阵是GNSS对流层层析解算的关键。对比常规方法和快速求解方法，2种方法的精度相当。当射线条数增多时，快速求解方法的解算效率明显提高。

[1] Flores A,Ruffini G,Rius A．4D Tropospheric Tomography Using GPS Slant Wet Delays[J]．Annales Geophysicae, 2000, 18(2):223-234

[2] 曹玉静,刘晶淼,梁宏,等．基于地基GPS层析大气水汽资源的方法研究[J]．自然资源学报,2010,25(10):1 786-1 796

[3] 陈宏斌．地基GPS层析水汽三维分布研究[D]．成都:西南交通大学,2014

[4] 胡金玉．基于CORS参考站对区域水汽的研究[D]．成都:西南交通大学,2014

[5] Siddon R．Fast Calculation of the Exact Radiological Path for a Three-Dimensional CT Array[J]． Medical Physics,1985,12(2):252-255

[6] 范士杰． GPS海洋水汽信息反演及三维层析研究[D]．武汉:武汉大学,2013

[7] 王晓英．地基GNSS层析对流层水汽若干关键技术研究[D]．南京:南京信息工程大学,2013

[8] 宋淑丽．地基GPS网对水汽三维分布的监测及其在气象学中的应用[D]．上海:中国科学院上海天文台,2004

[9] Censor Y． Finite Series-Expansion Reconstruction Methods[C]．Proceedings of the IEEE,1983, 71(3):409-419

[10] Christiaens M,Sutter B D,Bosschere K D,et al． A Fast, Cache-Aware Algorithm for the Calculation of Radiological Paths Exploiting Subword Parallelism[J]．Journal of Systems Architecture,1999, 45(10):781-790

P228.4

B

1672-4623（2016）06-0045-03

10.3969/j.issn.1672-4623.2016.06.015

杨飞，硕士，研究方向为区域对流层建模。

2015-06-30。

项目来源：国家自然科学基金资助项目（41474004）。