回到思维原点

[摘 要]
教学用书是教师教学的必备参考书,是教学的依据,然而教师应该有自己的思考,如果察觉其有疑惑之处,应及时予以探究,还原数学的本质面貌。“大道至简”也许能揭示一些数学规律,但简单中蕴含的不简单却要引起我们的关注。作为一名小学数学教师,在新课程推进的今天,不应仅仅是解题的能手,更应是追寻数学根源的探索者。
[关键词]
小学数学;探究;还原本质
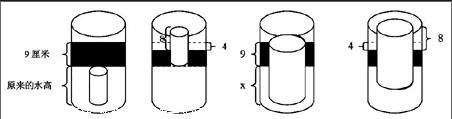
苏教版数学六年级下册第19页思考题:在一个圆柱形储水桶里,把一段底面半径为5厘米的圆柱形钢材全部放入水中,这时水面上升9厘米。把这段钢材竖着拉出水面8厘米,水面下降4厘米。求这段钢材的体积。
教学用书的解法是先算出储水桶的底面积:3.14×52×8÷4=157(平方厘米),然后算出圆钢的体积:157×9=1413(立方厘米)。
笔者开始也和教学用书的思路一样。在数学练习课放手让学生讨论一番,在学生的讨论中笔者方才发现其中值得推敲的地方甚多。“老师,如果圆钢的高度小于或等于储水桶原来水的高度,题目解法思路简单明了。”“老师,如果圆钢的高度与上升后水面高度齐平时,该如何考虑?”“老师,如果圆钢的高度大于储水桶原来水的高度而小于上升后水面高度时,又该如何考虑?”疑惑顿现,笔者静下心来,梳理了一番解题思路,察觉其需分析多种情况下题目的解题方法。下面就自己探究问题的历程与诸位共享。
图1 图2
一、解题之初,看山是山,看水是水
探讨一:当圆钢的高度小于或等于储水桶原来水的高度,见图1,教学用书上的解法显得非常清晰。教学用书的解法先算3.14×52×8÷4=157(平方厘米),是因为“拉出水面8厘米的圆钢体积等于下降4厘米水柱的体积”,由此算出储水桶的底面积,而上升9厘米的水柱体积等于圆钢的体积,所以用157×9=1413(平方厘米)求出圆钢的体积。不过值得注意的是这里的“水柱体积”应是“实心的,圆柱体的体积”,因为上升的水的形状会有多种情况出现,只是最后结论可统一为“上升或下降的水柱(实心的,圆柱体。以下所提水柱均为实心的圆柱体)体积等于圆钢的体积”。
当然,也可以换一种思路。圆钢拉出水面8厘米,水面就下降4厘米,可得“8厘米圆钢的体积等于下降4厘米水柱的体积”。把圆钢全部拉出水面,水面就下降9厘米,可得“圆钢的体积等于下降9厘米水柱的体积”,如果出现水面与圆钢齐平时,其结论也是一样的。这样,圆钢拉出水面的体积和下降的水柱的体积成正比例,用9÷4×8=18(厘米)求出圆钢的高度,再用3.14×52×18=1413(平方厘米)求出圆钢的体积。该种解法简洁明了,是正比例知识的灵活运用。让学生理解此种解法,可以使学生体味数学思考方法无所不在。数学教学中不但要知其然,还要知其所以然。
二、解题有悟,看山不是山,看水不是水
探讨二:当圆钢的高度与上升后水面高度齐平时,见图2,则“上升和下降的就是‘环形水柱而非‘水柱”“上升9厘米的环形水柱的体积是x厘米圆钢的体积”,有人理解为“上升9厘米的环形水柱的体积应是整段圆钢的体积而非x厘米圆钢的体积”是理解歧义所致。应理解为“上升9厘米的环形水柱的体积是x厘米圆钢的体积,同时加上9厘米圆钢的体积,可得上升的9厘米的水柱体积是整段圆钢的体积”,“把圆钢竖着拉出水面8厘米后,水面就下降4厘米”可得“(8-4)厘米圆钢的体积等于下降4厘米环形水柱的体积,同时加上4厘米的圆钢,得8厘米圆钢的体积等于下降4厘米水柱的体积”,由此用3.14×52×8÷4=157(平方厘米)先求出储水桶的底面积,再用157×9=1413(平方厘米)求出圆钢的体积。x厘米圆钢的体积能“挤高”9厘米的环形水柱,因为9厘米圆钢占据了自己的空间。
图3 图4 图5
探讨三:当圆钢的高度大于储水桶原来水的高度而小于上升后水面高度时,文中所提及的情况可分为三种。
第一种情况:以圆钢的上底面与水相交的截面为基准,上升的9厘米水分割成4厘米水(圆钢的上底面距现在水面的距离)和5厘米水(圆钢的上底面距原来水面的距离)。如图3,可知“下降4厘米的水柱体积等于8厘米圆钢的体积”,求得储水桶的底面积是3.14×52×8÷4=157(平方厘米)。“上升9厘米的水的体积(4厘米水柱的体积和5厘米的环形水柱的体积)等于截掉5厘米圆钢的体积,同时加上5厘米圆钢的体积,则上升9厘米水柱的体积等于整段圆钢的体积。”所以再用157×9=1413(平方厘米)求出圆钢的体积。
第二种情况:上升的9厘米水分割成上面m(大于4)厘米水和下面n(小于5)厘米水。如图4,可知“下降4厘米的水柱体积等于8厘米圆钢的体积”,求得储水桶的底面积是3.14×52×8÷4=157(平方厘米)。“上升9厘米的水的体积(m厘米水柱的体积和n厘米的环形水柱的体积)等于截掉n厘米圆钢的体积,同时加上n厘米圆钢的体积,则上升9厘米水柱的体积等于整段圆钢的体积。所以再用157×9=1413(平方厘米)求出圆钢的体积。
第三种情况:上升的9厘米水分割成上面m(小于4)厘米水和下面n(大于5)厘米水。如图5,可知“下降4厘米的水的体积,即m厘米水柱的体积和(4-m)厘米环形水柱的体积等于(8-4+m)厘米圆钢的体积,同时加上(4-m)厘米圆钢的体积,则下降4厘米水柱的体积等于8厘米圆钢的体积”。我们也可以换一个角度来分析,把图5“圆钢竖着拉出水面8厘米”改为“把圆钢先向上拉至和水面齐平,因为是在水中运动,总体积不变,所以水面高度没有变化,如同图2的左图,再把圆钢向上拉出水面8厘米,水面下降4厘米,可得“(8-4)厘米圆钢的体积等于下降4厘米水柱的体积,同时加上4厘米的圆钢,得8厘米圆钢的体积等于下降4厘米水柱的体积”,求得储水桶的底面积是3.14×52×8÷4=157(平方厘米)。“上升9厘米的水的体积(m厘米水柱的体积和n厘米的环形水柱的体积)等于截掉n厘米圆钢的体积,同时加上n厘米圆钢的体积,则上升9厘米水柱的体积等于整段圆钢的体积”。所以再用157×9=1413(平方厘米)求出圆钢的体积。
三、解题彻悟,看山仍然山,看水仍然是水
殊途同归,以上诸多的情况,分析思路不一,但都回到了思考的原点——“下降4厘米的水柱体积等于8厘米圆钢的体积,上升9厘米水柱的体积等于整段圆钢的体积”。此时,笔者不由得要重新审视自己的解题思路,“解决问题的策略——转化法”,不就是我们平时教学中常用的数学方法吗?终于豁然开朗,思维原点图在我脑海里呈现。以上5种情况,只要把圆钢截成若干段,全部放入原来的水面下,这样“上升9厘米水柱的体积等于整段圆钢的体积”;把圆钢竖着拉出水面8厘米后,水面就下降4厘米,可以转化成“截掉8厘米的圆钢,剩余的圆钢全部放入原来的水面下”,这样“下降4厘米的水柱体积等于8厘米圆钢的体积”。如此,还原出数学本质。就在我欣慰之际,“如果圆钢的体积足够大时,截成若干段不能全部放入原来的水面下”,那又必须回归到上述的各种情况,然后再回到思维原点。真是教无定法,数学分析方法千变万化,但只要理解了数学方法中所渗透的数学思想,则万变不离其中,数学智慧由此凸显其价值取向。
经历了千山万水,终于还原了数学的本质面貌,关于此类问题的争论也可告一段落。教学用书的解题方法固然是正确的,但其中蕴含的数学思想和方法只有靠数学教师自己去探寻、思索。“大道至简”也许能揭示一些数学规律,但简单中蕴含的不简单却要引起我们的关注。作为一名小学数学教师,在新课程推进的今天,不应仅仅是解题的能手,更应是追寻数学问题根源的探索者。
[参 考 文 献]
[1]胡作玄.数学是什么[M].北京:北京大学出版社,2008(6).
[2]刘彦平.谈谈小学生数学应用题解题能力的培养[J].中小学数学(小学版),2014(7-8).
(责任编辑:李雪虹)
作者简介:王玉兰(1973-),女,江苏射阳人,小学高级教师,大学本科。研究方向:小学数学教学。

