Numerical study on the effects of progressive gravity waves on turbulence*
Anqing (Elliott) XUAN, Bingqing DENG, Tao CAO, Lian SHEN
Department of Mechanical Engineering and Saint Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN, USA, E-mail: xuanx004@umn.edu
Numerical study on the effects of progressive gravity waves on turbulence*
Anqing (Elliott) XUAN, Bingqing DENG, Tao CAO, Lian SHEN
Department of Mechanical Engineering and Saint Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN, USA, E-mail: xuanx004@umn.edu
The wind-wave-ocean system, which contains complex interactive processes, is of great importance for the momentum, heat and mass transport in the atmosphere and ocean and at their interface. In this work, we perform wave-coupled phase-resolved numerical simulations to investigate the effect of progressive gravity waves on wind and ocean turbulence. Initially homogeneous turbulence under a finite-amplitude monochromatic surface wave is simulated to reveal how the wave influences the subsurface turbulence. For the interaction between wind-driven waves and shear turbulence in the ocean, new wave-phase-resolved simulation approaches are developed to capture Langmuir cells. Lastly, wind turbulence over one and two progressive waves is simulated to elucidate the dynamics of turbulence coherent structures impacted by surface waves for improved understanding of wind-wave growth mechanism.
wave-ocean interaction, Langmuir circulation, wave-wind interaction, numerical simulation
Introduction
Turbulence in the wind-wave-ocean system involves many complex processes. Waves can substantially modify the turbulent flows, resulting in many distinct features, such as, Langmuir cells on the ocean side and critical layer on the air side. The turbulence can in turn affect ocean currents and waves. The coupling dynamics plays an important role in the momentum, heat, and mass fluxes at sea surfaces and the transport and mixing in the oceanic mixed layer and marine atmospheric boundary layer. Despite its importance, the dynamics of turbulence in the wave environment has largely been elusive due to the complexity of the physical problem.
Considerable studies have been performed to investigate the subsurface turbulence in the presence of surface waves. It has been found that turbulence intensity can be enhanced by wave-turbulence interaction[1,2]. Waves can also contribute to the stretching and tilting of turbulence vortices[3,4]. Meanwhile, turbulence has been shown to become wave-phase depe-ndent under the modulation of waves[1,4-6]. It is therefore desirable to study the wave-turbulence interaction using wave-phase-resolved simulations, which have been made possible with the increase in computing resources and the recent development of numerical methods[7-9].
The interaction between surface waves and winddriven turbulence can generate Langmuir cells[10-12], which is one of the most important turbulence processes in the upper ocean. Langmuir cells can be manifested by windrows on the surface, which are the amalgamation of buoyant materials driven by pairs of counter-rotating vortices aligned with the wind. The downward and upward convection by the vortices can significantly affect the mixing and transport processes in the mixed layer. Traditionally, numerical simulations of Langmuir cells have been limited to a wavephase-averaged description using a Craik-Leibovich equations with a rigid-lid approximation[13-15]. The wave effect on the long-term evolution of the turbulent flow is modeled through a vortex force involving the Stokes drift. However, such model may oversimplify the complex system by overlooking the wave phase information and the correlation between waves and turbulence fluctuations. This limitation motivates us to develop and perform large-eddy simulation (LES) of Langmuir turbulence with explicitly resolved wavesto capture more accurately the wave-turbulence interaction dynamics.
Wind-wave interaction is important in many applications and critical for the fundamental understanding of the wind wave growth mechanism. It has been found that the turbulent coherent structures and the related Reynolds stresses over progressive surface waves are characterized by wave-phase-correlated turbulence fluctuations. Belcher and Hunt[16]and Cohen and Belcher[17]proposed a non-separated sheltering mechanism to relate the wave-phase-correlated turbulent stress to the growth of the waves. As a consequence, a detailed understanding of turbulent structures in the vicinity of surface waves was obtained. The turbulence over two progressive surface waves is far more complicated than that over one surface wave, because the wave-phase-correlated turbulent motions induced by two different surface waves can interact with each other. Chen and Belcher[18]performed a theoretical analysis at extremely high Reynolds numbers, and showed the importance of the sheltering effect with a decrease of the form drag on short waves due to the reduction of the turbulent stress over the short waves in the presence of a long wave. This theory shed lights on the understanding of the generation of surface waves in the presence of long waves, but still needs more study to be validated. In our study, one of the tasks is to perform numerical simulations for wind turbulence over one and two surface waves to improve the understanding of the effect of progressive waves on turbulent structures.
This paper aims at using high-fidelity and highresolution data from wave-coupled phase-resolved simulations to obtain an improved understanding of the fundamental mechanisms of wave effects on the wind and ocean turbulence. First, the interaction between sur-face progressive waves and initially isotropic turbulence underneath is studied using direct numerical simulation (DNS). We focus on the mechanistic study of the effect of a finite-amplitude monochromatic wave on the subsurface turbulence. Then, Langmuir turbulence is studied with two advanced wave-phaseresolved numerical simulation approaches. Finally, the effects of progressive waves on the wind turbulence are investigated.
1. Mechanistic study of wave-turbulence interaction
In this section, we focus on the interaction of initially homogeneous turbulence with surface progressive waves. To capture the sea-surface boundary effects and wave nonlinearity, we perform DNS on a wavesurface-fitted curvilinear grid that moves with the dynamically-evolving wave surface subject to fully nonlinear kinematic and dynamic free-surface boundary conditions[9]. As a result, the wave profile and orbital motions are explicitly resolved, in contrast to the rigid-lid approximation and Stokes drift treatment used in previous studies. Fourier-based pseudo-spectral method in the horizontal directions and finitedifference method in the vertical direction are used for spatial discretization, and a second-order fractionalstep scheme is used for temporal integration. Statistically steady isotropic homogeneous turbulence is generated in the bulk flow by a random forcing method[19,20]. The turbulence is then distorted by surface waves with various wave steepness and frequency. The turbulence-to-wave length ratio is 0.109, and the turbulence-to-wave time ratio ranges from 2.58 to 11.5, corresponding to immediate to rapid distortion regimes. A gentle pressure is applied on the surface to dynamically adjust and maintain the progressive waves to obtain a statistically steady state. Detailed problem setup and parameters can be found in the works of Guo and Shen[6,21].
The statistics of our simulation data show that the magnitude and orientation of turbulent vortices vary with the wave phase. The vertical vortices are tilted toward the wave propagating direction under the wave crest, and are tilted backwards under the wave trough. In other words, as a wave passes by, vertical vortices are tilted back and forth. However, it is found that there exists a net tilting of vertical vortices to the wave propagation direction, which can be attributed to the Stokes drift of waves and the correlation between turbulence and wave strain rate[21]. The tilting of vortices is closely related to the role of waves in the initial formation of Langmuir cells. Horizontal vortices also experience periodic tilting, but the net effect is close to zero.
The intensities of turbulence velocity fluctuations are also found to vary with wave phases. Take phasedependent averaged streamwise velocity fluctuations intensityas an example. Away from the surface,reaches its maximum under the wave trough and minimum under the wave crest. This result is consistent with previous theoretical analysis using the rapid distortion theory[4]. The variation near the surface, however, is opposite to the theoretical prediction. Our analysis of the budget ofshows that the variation of velocity fluctuations is dominated by the normal production associated with the mean wave strain rate, pressure-strain correlation, and pressure transport. The production term in the budget equation,increasesunder the forward slope, and the opposite process happens below the backward slope. Near the surface, both the pressure-strain correlationand pressure transportterms are negative under the forward slope and positive under the backward slope. Therefore, near the surface, thepressure-related terms reverse the energy distribution process caused by the wave production term, resulting in the deviation from the previous theory[6].
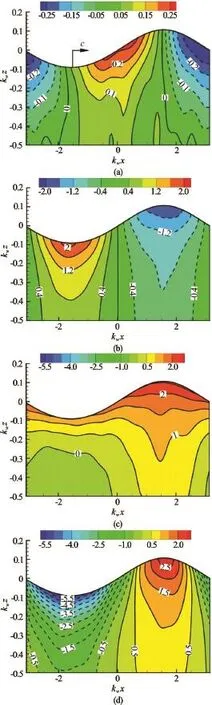
Fig.1 Contours of (a) Reynolds shear stressand terms in the budget equation for(b) Wave production(c) Velocity-pressure-gradientand (d) Velocity-pressure-gradient
The propagation of waves also results in a wavephase dependent distribution of the Reynolds shear stress. As shown in Fig.1(a), the shear stressis positive under the wave backward slope and negative under the forward slope. The distribution ofis not symmetric, and the Lagrangian averagedis non-zero, indicating a net shear stress exerted by the progressive wave. The budget of Reynolds shear stress is dominated by a production term related to wave shear strain, and velocity-pressure-gradient terms related to the pressure fluctuations (Figs.1(b)-1(d)). The production term⋅is negative under the wave crest and positive under the trough. The velocity-pressure-gradient termis positive under the crest and negative under the trough. The other termis always positive but has a smaller magnitude. A comparison of the magnitudes of different terms shows that the variation of Reynolds shear stress is mainly determined by the velocity-pressuregradient terms, whereas the production term offsets the effects of pressure. This result suggests that the pressure, which is related to the kinematics of wave surface, is important in the turbulence dynamics near the surface.
2. Simulation of Langmuir turbulence
The present study performs LES of Langmuir turbulence with the waves explicitly resolved, and thus obtains more information on the wave-turbulence interaction dynamics. Our phase-resolved LES employs two different advanced numerical approaches: (1) wave-surface-fitted simulation as mentioned above with subgrid-scale (SGS) modeling, and (2) wavedirectly-forcing simulation, which can couple the phase-dependent wave forcing with the simulation of turbulent flows. The advantage of the first approach is its ability to reveal the fundamental mechanism of the generation of Langmuir cells because of its ability to directly resolve the wave surface with nonlinear freesurface boundary conditions. The second approach is derived based on the assumption of potential surface waves. Using Helmholtz’s decomposition, the fluid motions are decomposed into a potential flow part and a rotational part. The potential part corresponds to the surface waves, and the rotational part indicates the turbulence flow with an additional wave-phase-dependent vortex forcing term in the Navier-Stokes equations standing for the influence of waves. The potential wave motions satisfy the kinematic boundarycondition and the surface-normal dynamic boundary condition. The potential part is simulated by the highorder-spectral method (HOS)[22]. The rotational velocity is responsible for the balance of surface-tangential stresses. The boundary conditions of the rotational velocity are further expanded into terms of surface amplitudes at the averaged surface height, and hence a regular Cartesian grid can be used. Because HOS can compute the nonlinear interaction of surface waves and because a Cartesian grid is used for the turbulence flow simulation, the second approach can simulate Langmuir cells beneath realistic waves with high computational efficiency.
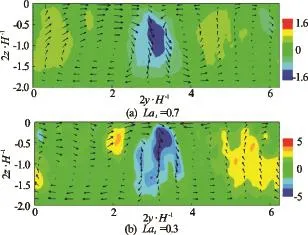
Fig.2 Contours of instantaneous streamwise averaged vertical velocityThe vectors indicate the velocity component

Fig.3 Distribution of surface parcels after released randomly
In Langmuir turbulence, the relative importance of the Stokes drift to the shear force is quantified by the turbulent Langmuir number, defined as, withu∗being the friction velocity andbeing the Stokes drift velocity at the surface. A variety of turbulent Langmuir numbers have been considered in our study. After averaging over the streamwise direction, the counter-rotating structure emerges from the wave-surface-fitted simulation (i.e., the aforementioned first approach) as shown in Fig.2. The downwelling region is below the surface convergence zone, and the strength of the downwelling motion is increased as Latdecreases (i.e., with stronger wave forcing). Figure 3 shows the surface structures of the convergence zones (windrows) using particles. Initially, particles are randomly released onto the surface. After some time, most particles aggregate into narrow bands due to the converging effects. We can also observe the joining of windrows, which is in consistence with previous observations and other numerical simulations.
Figure 4 shows the instantaneous streamwise velocity of Langmuir turbulence interacting with a monochromatic wave train solved by the wave-directly-forcing method (i.e., the aforementioned second approach). Long streaks are generated at the surface, and the influence of wave phase is also exhibited. The large-scale regions of high speed and low speed in the frontal cross-wind plane indicate the upwelling and downwelling of large-scale Langmuir cells.

Fig.4 Contour of instantaneous streamwise velocity fluctuation u′

Fig.5(a) Surface elevations of JONSWAP waves
Using the wave-directly-forcing approach, we have also simulated the formation and evolution of Langmuir cells in broadband wave field for the first time. Fig.5(a) shows the surface elevation of JONSWAP waves, and Fig.5(b) shows the particles on the surface after a short time of the onset of Langmuir cells. The particles are initially distributed homogeneously on the surface, and then are quickly gathered into windrows by the Langmuir cells.

Fig.5(b) Particles on the surface
3. Wind over progressive waves
To study the influence of surface waves on wind turbulence, we carry out DNS of stress-driven turbulent Couette flow over one and two waves as a canonical problem of wind-wave interaction. In the one surface wave cases, airy waves and Stokes waves are considered and compared with stationary wavy walls and vertically waving walls. Different wave steepness values (ak=0.1, 0.2, 0.25) are considered. In the two wave cases, we prescribe the wavelength ratio,λl/ λs=4, which is the ratio of the wavelength of the long wave to that of the short wave, and other parameters of these two waves are determined by the JONSWAP relationship. For the effect of wave age, c/ u∗, which is the ratio of the wave phase speed to the friction velocity of the wind, we investigate three representative cases,c/ u∗=2, 14, and 25, in both one and two wave cases, corresponding to slow, intermediate, and fast waves, respectively.
3.1 Wind over one progressive wave
In addition to the geometrical effect of the wavy surface, the motion of sea surface substantially changes the flow features of wind and increases the complexity of the turbulence in the vicinity of waves. Our study shows that the turbulence flow structures in the vicinity of water waves highly depend on the wave age and wave steepness. Vortex structures for the slow wave cases are characterized by the reversed horseshoes concentrated over wave trough and the quasistreamwise vortices mainly over the windward face of the wave (Fig.6). For intermediate and fast wave cases, the vortex structures are dominated by bent quasistreamwise vortices, which have a downward bending in their upstream ends near the wave trough[23]. These vortex structures have a large influence on the Reynolds stress distribution over waves. Detailed examination of Reynolds stress with quadrant analysis, turbulence kinetic energy (TKE), and TKE budget shows large variations with the wave phase; and the variations are highly dependent on the wave age and wave nonlinearity. Comparison of Airy waves with Stokes waves shows that the higher order wave components can make an appreciable difference to turbulent structures[24].

Fig.6 Instantaneous vortex structures in turbulent wind over waves. Wave steepness ak =0.25, wave age(a) Iso-surfaces of the tensorwhere S andΩare respectively the symmetric and anti-symmetric parts of the velocity gradient tensor, (b) Vectors of horizontal and vertical velocity fluctuations (u′,w′) on the left vertical cross-section in (a)
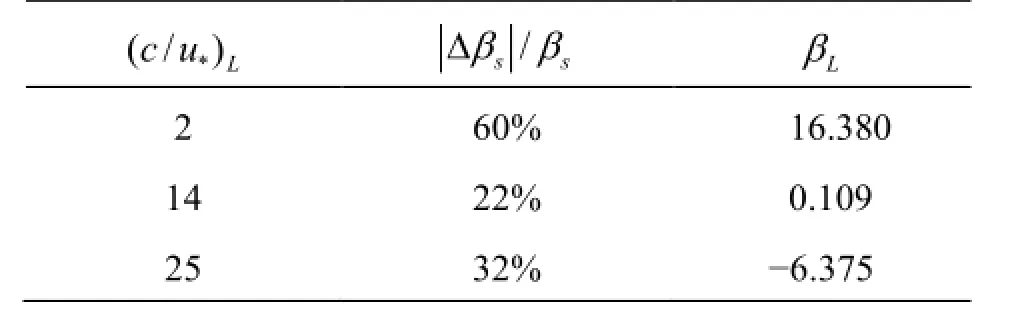
Table 1 Comparison of wave growth rate of short wave with and without long wave
3.2 Wind over two progressive wave

To further examine the mechanism of the reduction of the wave growth rate of the short wave, we carry out the energy conservation analysis in the wave boundary, and it shows that the sheltering effect is related to the production of turbulence energy at the short wave scale and thus the Reynolds stress corresponding to the short wave. In the slow wave case, the Reynolds stress at the short wave scale is reduced in the presence of the long wave (Fig.7(a)), and thus the production of TKE is reduced, so is the energy flux from the wind to the short wave. As a result, the form drag on the short wave is reduced. In the fast wave case, the Reynolds stress corresponding to the short wave is enhanced by the long wave (Fig.7(b)), but the direction of energy flux is from the short wave to the wind. The increase of turbulence production leads to a reduction of energy flux from the short wave to the wind. Therefore, for the fast wave case, the form drag on the short wave is also reduced, which leads to a reduction of the magnitude of the wave growth rate of the short wave.

Fig.7 The amplitudes of Reynolds stresses on the short wave
4. Conclusions
In this work, the influence of progressive gravity waves on turbulence, including ocean and wind turbulence, is investigated by performing wave-coupled phase-resolved numerical simulations. The interaction between surface progressive waves and isotropic turbulence is studied to reveal the underlying mechanism how the finite-amplitude monochromatic wave affects the subsurface turbulence. New simulation strategies are developed for Langmuir turbulence resulted from the interaction of surface waves with wind-driven shear turbulence. The influence of surface waves on wind turbulence is analyzed for the cases with one and two progressive waves.
The mechanistic study of wave-turbulence interaction based on the wave-phase-resolved DNS in a surface-fitted coordinate provides substantial information on the effects of waves on the subsurface turbulence. Turbulence statistics, including vorticity, kinetic energy, and Reynolds shear stress, shows strong wavephase-dependence due to the wave distortion. Both streamwise and vertical vortices are found to be tilted by the wave periodically. However, the Stokes drift and wave-turbulence correlation result in a net turning of the vertical vortices towards the wave propagation direction, whereas the accumulative turning of streamwise vortices is negligible. Away from the surface, the variation of streamwise turbulence intensity is mainly dominated by the production by wave strain rate, which leads to maximum intensity under the wave trough and minimum under the wave crest. Near the surface, however, the energy distribution is reversed by pressure-strain correlation and pressure transport terms. The Reynolds stress, modulated by waves, is found to be respectively positive and negative under the backward and forward wave slopes. The analysis on budget reveals that the variation is controlled by wave shear production and velocity-pressure-gradient correlation.
Two simulation strategies are developed to preform phase-resolved LES of Langmuir cells resulted from the interaction of wind-shear-driven turbulence and surface waves in the upper ocean. One approach uses the surface-fitted grid and fully nonlinear surface boundary condition. This method can accurately resolve Langmuir turbulence, and hence is of great importance for investigating the underlying dynamic mechanism and validating the existing theories. Another approach uses Helmholtz’s decomposition to decompose the flow field into rotational and potential parts. The potential part corresponds to potential surface waves, which satisfy the kinematic boundary condition and the surface-normal dynamic boundary condition, and is simulated by the HOS method. The rotational part represents the turbulence, and is influenced by surface waves through a wave-phase-dependent vortex forcing term. The rotational part satisfies the balance of surface-tangential stresses at the surface, which is then expanded into terms of surface amplitudes at the averaged surface height for simplification. Due to thesimplified boundary condition for turbulence and the usage of the HOS method for nonlinear surface waves, this method can simulate Langmuir cells in the presence of realistic waves with high computational efficiency. The simulation results indicate that both these two methods can successfully capture Langmuir cells.
Lastly, wave-boundary-fitted DNS turbulence solver previously developed by Yang and Shen[9]is employed to study the turbulence structure over surface waves. Using DNS, the vortex structures over various progressive waves are studied in detail. We also study the turbulent flow over two progressive waves and the sheltering effect of the long wave on the short wave was confirmed under a relatively low Reynolds number. We also study the mechanism of the sheltering effect by energy conservation analysis and show that this sheltering effect is related to the change of Reynolds stress at the short wave scale.
Acknowledgement
This work was partially supported by the NSF (Grant Nos. 1341062, 1341063 and 1605080) and the ONR CASPER MURI project.
[1] Rashidi M., Hetsroni G., Banerjee S. Wave-turbulence interaction in free-surface channel flows [J]. Physics of Fluids A Fluid Dynamics, 1992, 4(12): 2727-2738.
[2] Thais L., Magnaudet J. Turbulent structure beneath surface gravity waves sheared by the wind [J]. Journal of Fluid Mechanics, 1996, 328: 313-344.
[3] Phillips O. M. A note on the turbulence generated by gravity waves [J]. Journal of Geophysical Research Atmospheres, 1961, 66(9): 2889-2893.
[4] Teixeira M. A. C., Belcher S. E. On the distortion of turbulence by a progressive surface wave [J]. Journal of Fluid Mechanics, 2002, 458: 229-267.
[5] Jiang J., Street R. L. Modulated flows beneath windruffled, mechanically generated water waves [J]. Journal of Geophysical Research Atmospheres, 1991, 96(C2): 2711-2721.
[6] Guo X, Shen L. Numerical study of the effect of surface wave on turbulence underneath. Part 2. Eulerian and Lagrangian properties of turbulence kinetic energy [J]. Journal of Fluid Mechanics, 2014, 744: 250-272.
[7] Hodges B. R., Street R. L. On simulation of turbulent nonlinear free-surface flows [J]. Journal of Computational Physics, 1999, 151(2): 425-457.
[8] Komori S., Kurose R., Iwano K. et al. Direct numerical simulation of wind-driven turbulence and scalar transfer at sheared gas-liquid interfaces [J]. Journal of Turbulence, 2010, 11: 1-20.
[9] Yang D., Shen L. Simulation of viscous flows with undulatory boundaries. Part I: Basic solver [J]. Journal of Computational Physics, 2011, 230(14): 5488-5509.
[10] Craik A. D. D., Leibovich S. A rational model for Langmuir circulations [J]. Journal of Fluid Mechanics, 1976, 73: 401-426.
[11] Leibovich S. On the evolution of the system of wind drift currents and Langmuir circulations in the ocean. Part 1. Theory and averaged current [J]. Journal of Fluid Mechanics, 1977, 79: 715-743.
[12] Thorpe S. A. Langmuir circulation [J]. Annual Review of Fluid Mechanics, 2004, 36(1): 55-79.
[13] McWilliams J. C., Sullivan P. P., Moeng C. H. Langmuir turbulence in the ocean [J]. Journal of Fluid Mechanics, 1997, 334: 1-30.
[14] Skyllingstad E. D., Smyth W. D., Crawford G. B. Resonant wind-driven mixing in the ocean boundary layer [J]. Journal of Physical Oceanography, 2000, 30(8): 1866-1890.
[15] Tejada-Martínez A. E., Grosch C. E., Gargett A. E. et al. A hybrid spectral/finite-difference large-eddy simulator of turbulent processes in the upper ocean [J]. Ocean Modelling, 2009, 30(2-3): 115-142.
[16] Belcher S. E., Hunt J. C. R. Turbulent shear flow over slowly moving waves [J]. Journal of Fluid Mechanics, 1993, 251: 109-148.
[17] Cohen J. E., Belcher S. E. Turbulent shear flow over fastmoving waves [J]. Journal of Fluid Mechanics, 1999, 386: 345-371.
[18] Chen G., Belcher S. E. Effects of long waves on windgenerated waves [J]. Journal of Physical Oceanography, 2000, 30(9): 2246-2256.
[19] Rosales C., Meneveau C. Linear forcing in numerical simulations of isotropic turbulence: Physical space implementations and convergence properties [J]. Physics of Fluids, 2005, 17(9): 095106.
[20] Guo X., Shen L. On the generation and maintenance of waves and turbulence in simulations of free-surface turbulence [J]. Journal of Computational Physics, 2009, 228(19): 7313-7332.
[21] Guo X., Shen L. Numerical study of the effect of surface waves on turbulence underneath. Part 1. Mean flow and turbulence vorticity [J]. Journal of Fluid Mechanics, 2013, 733: 558-587.
[22] Dommermuth D. G., Yue D. K. P. A high-order spectral method for the study of nonlinear gravity waves [J]. Journal of Fluid Mechanics, 1987, 184: 267-288.
[23] Yang D., Shen L. Characteristics of coherent vortical structures in turbulent flows over progressive surface waves [J]. Physics of Fluids, 2009, 21(12): 125106.
[24] Yang D., Shen L. Direct-simulation-based study of turbulent flow over various waving boundaries [J]. Journal of Fluid Mechanics, 2010, 650: 131-180.
(Received June 30, 2016, Revised November 1, 2016)
* Biography:Anqing (Elliott) XUAN (1991-), Male, Ph. D. Candidate
Lian SHEN,
E-mail: shen@umn.edu
- 水动力学研究与进展 B辑的其它文章
- Development of an adaptive Kalman filter-based storm tide forecasting model*
- Development of Cartesian grid method for simulation of violent ship-wave interactions*
- Experimental tomographic methods for analysing flow dynamics of gas-oilwater flows in horizontal pipeline*
- Energy saving by using asymmetric aftbodies for merchant ships-design methodology, numerical simulation and validation*
- Coupling of the flow field and the purification efficiency in root system region of ecological floating bed under different hydrodynamic conditions*
- Modelling hydrodynamic processes in tidal stream energy extraction*

