Wavy properties and analytical modeling of free-surface flows in the development of the multi-domain method*
Xiaobo CHEN, Hui LIANG
Deepwater Technology Research Centre, Bureau Veritas, Singapore 117674,
E-mail: xiao-bo.chen@bureauveritas.com
Wavy properties and analytical modeling of free-surface flows in the development of the multi-domain method*
Xiaobo CHEN, Hui LIANG
Deepwater Technology Research Centre, Bureau Veritas, Singapore 117674,
E-mail: xiao-bo.chen@bureauveritas.com
The wavy (oscillatory both in space and in time) properties of free-surface flows due to presence of floating bodies are analyzed within the framework of the potential-flow theory by assuming that the fluid is perfect and flow irrotational. A so-called new multi-domain method has been developed based on the fluid domain division by an analytical control surface surrounding bodies and the application of different methods adapted in the external and internal domains. In the analytical domain external to the control surface, the fundamental solution satisfying the linear boundary condition on the free surface associated with a point singularity (often called Green function and referred here as point solution) is applied to capture all wavy features of free-surface flows extending horizontally to infinity. Unlike classical studies in which the control surface is discretized, the unknown velocity potential and its normal derivatives are expressed by expansions of orthogonal elementary functions. The velocity potential associated with each elementary distribution (elementary solutions) on the control surface can be obtained by performing multi-fold integrals in an analytical way. In the domain internal to the control surface containing the bodies, we could apply different methods like the Rankine source method based on the boundary integral equations for which the elementary solutions obtained in the external domain playing the role of Dirichlet-to-Neumann operator close the problem.
analytical modeling, multi-domain method, point solution (PS), elementary solution (ES), body solution (BS)
Introduction
We consider one or several bodies floating on the free surface which is extended horizontally to infinity. The major issues of such free-surface hydrodynamics include the fluid viscous effect, the non-linearities and wavy behaviors of the free surface. The real flow described by Navier-Stokes equations has viscous effect which plays a critical role in flow separation, generation and movement of vorticity, turbulence, pressure distribution, and dissipation. The viscous effect is of great importance in the resistance computation useful for hull optimizations, the estimation of viscous damping coefficient introduced to roll motions, and wind/ current coefficients to approximate wind/current loading. Non-linearities associated with body’s large motions and with free-surface boundary conditions are intrinsic in the real flow and in the non-viscous flowby ignoring viscous effect. In modeling flows of large amplitude or violent phenomena like greenwater, water impact, wave run-up, etc., the non-linearities are evident. Significant progress has recently been made to model viscous flows by computational fluid dynamics (CFD) and in non-linear computations of potential flows, thanks to the amazing development of powerful computation resources. However, still a reliable and practical method is missing in the modeling of wavebody interaction like seakeeping of ships advancing in waves. One major reason is associated with the peculiar properties of free-surface flows which are oscillatory and dispersive. It is easy to understand that most advanced numerical algorithms in CFD are merely useful to capture wavy flows since the dimension of meshed domain should be large enough to contain several waves while the mesh (cell or finite volume) size should be sufficiently small to capture complex flow of vorticity. Recent research has thus oriented to develop multi-domain methods to combine different approaches to model the viscous effect and non-linearities on one side and to take care of wavy flow on the other side.
The dynamic balance between the inertial force of moving water mass and the restoring force due to the gravity makes the free surface rise up and fall down surrounding the perturbation. Free-surface elevations (waves) propagate and carry energy away from the perturbation. Depending on the wavelength, the oscillatory behavior of flow can persist very deep beneath the free surface. Understanding the wavy properties of free-surface flows is essential and critical to study the wave-body interaction for evaluating wave loads and predicting body’s responses. Indeed, three classes of issues in the fluid-structure interaction include viscous effect, non-linearities and wavy behavior of the free surface, of which the last is not the least.
It is reasonable to accept the assumption that the viscous effect and non-linearities are negligible at some distance from bodies. Classical works based on the Laplace equation and the linearized boundary condition on the free surface have been very successful in giving the fundamental solution often called Green function associated with a point singularity-choice of singularity depending on the treated problem. For this reason, we like to refer the Green function as the point solution (PS). PS can be distributed on some surface (usually on the body surface) to form a complete solution which satisfies all boundary conditions including that on the body surface by using the boundary integral equation to determine the density of distribution, and is referred as body solution (BS). Being a distribution of PS, BS is deemed to have similar properties with PS. However, it could not be the case in reality.
For the modeling of wave radiation and diffraction around bodies, the conventional approach is the boundary element method (BEM) associated with the free-surface Green function which is required to integrate over each discretized panel to seek BS[1]. This method works well in some particular problems like wave-body interaction without the forward speed. Unfortunately, it fails to be generalized to the problem of the free-surface flow induced by a ship advancing in waves. The main reason lies in the complexly singular and highly oscillatory behaviors of PS when both field and source points are in the vicinity of the free surface[2], or waves near the origin of impulsive point are found to diminish continually in length and to increase continually in height. These peculiar properties are manifestly non-physical. The integration of PS over a meshed panel or along a line segment giving the building block (influence coefficients) of the boundary integral equations, inherits the similar singularity and highly oscillatory properties. In the limit of smaller and smaller panels (shorter and shorter segment), the integral equation should be more ill-conditioned and could not produce correct and convergent results. Nevertheless, BS should be totally different or at least the leading terms (singularities and high oscillations) might be cancelled out due to destructive interference effect in the integration of PS according to Lamb[3].
In order to overcome above-mentioned difficulties, we consider the multi-domain methodology. The fluid domain is divided by a control surface into the internal domain where the floating body is present and external domain. The control surface can be in the form of a hemi-ellipsoid, a hemi-sphere, a truncated vertical cylinder with bottom or an infinite vertical cylinder in deepwater. In the external domain without the presence of floating bodies, the free-surface Green function can be used to represent the wavy properties of the free surface, while the Rankine source method is applied in the internal domain. Different from the traditional domain decomposition strategy, the control surface is not panelized in the present multi-domain method, on which the velocity potential and its normal derivative are expanded into the sum of elementary functions. The boundary integral equation imposed on the control surface is obtained by Galerkin collocation involving a series of test functions orthogonal to the elementary functions. Unlike classical methods, the free-surface Green function is not explicitly evaluated but its integration over the control surface is computed analytically. The elementary solutions (ES) obtained in this way build the relationship between velocity potential and its normal derivative which is called the Dirichlet-to-Neumannoperator. Thisoperator can be directly used in the coupling with equations in the internal domain through continuous conditions on the control surface.
In terms of implementation, Ten and Chen[4]adopted a hemi-sphere as the control surface and elementary functions consist of Legendre polynomials and Fourier series. For the purpose of simplification, Liang and Chen[5]used a circular cylinder as the control surface to keep the independence of horizontal and vertical variables, and the velocity potential and its normal derivative are expressed in the form of Fourier-Laguerre series. This approach has been capable of solving the wave radiation and diffraction problems with zero forward speed free of irregular frequencies[5]. Chen et al.[6]studied the transient disturbance caused by a vertical cylinder and found that PS is highly oscillatory with large amplitude while ES is smooth and well-behaved. Indeed, the multi-domain method combines the advantages of both the Rankine panel method and that based on the free-surface Green function. The difficulties associated with peculiar properties of complex singularities[2]are solved by the integration of the free surface Green function on the control surface. Furthermore, the internal domain is a finite domain and thus the Rankine panel method is well suited and efficient.
It is worth noting that the multi-domain method is not limited to couple the Rankine source methodand the method based on the free-surface Green function within the framework of the potential-flow theory. It can also be generalized to couple the CFD method accounting for the viscous effect and potentialflow solver. In this case, an intermediate domain between the external domain and internal domain is necessary to make a smooth transition from viscous or/and non-linear problem to the linear free-surface wavy problem. Figure 1 shows a typical sketch of the multi-domain methodology where the fluid domain is divided into three domains including: the internal domain, transit domain and external domain. In the internal domain where the body is present, the viscous as well as nonlinear effects play a predominant role, and the numerical algorithms used in CFD are well suited for local flows in the vicinity of bodies. In the transit domain, the viscous effect is out ruled and the nonlinear problem is smoothly transited to the linear one. In the external domain, both viscosity and nonlinearity are ignored so that the linear potential-flow solver can be applied, and semi-analytical solutions ensure the wavy behavior of free-surface flows to be consistent and accurate.

Fig.1 Sketch of the multi-domain methodology by dividing the fluid domain into three domains
In the present article, the method to predict the free-surface flow around floating bodies based on the free-surface Green function is first outlined, and the features of PS and BS are described, respectively. In particular, different features of PS and BS are analyzed. Then, a brief introduction of the multi-domain method is presented, and the progress that we made on the multi-domain method is reported.
1. Green function method
Free-surface flows featured with wavy properties are quite common in the field of marine and offshore hydrodynamics. One mainstream method is based on BEM associated with the free-surface Green function. This approach was extensively studied in the past several decades. Due to the fact that the free-surface Green function satisfies not only the governing equation but also the free-surface and radiation conditions, the boundary integral equation over all boundary surfaces can be reduced to the integral over the body surface (and the waterline if necessary) only which greatly reduces the number of unknowns. Besides, the utilization of the free-surface Green function can effectively avoid dispersion errors caused by the discretization of the free surface[7].
Essentially, the free-surface Green function (PS) is an expression of a source potential with unit strength satisfying one specific free-surface boundary condition as well as the radiation condition in the far field, and various types of free-surface Green functions are collected by Wehausen and Laitone[8]. PS can be distributed over boundary surfaces (usually on the body surface) to form a complete solution which satisfies all boundary conditions including that on the body surface by using the BEM to determine the density of distribution. In this way, BS can then be considered as a linear superposition of PS.
1.1 Point solution
PS can be obtained by applying the Fourier transform to free-surface boundary condition of the problem and is then expressed in the form of a double Fourier integral in the Fourier plane (a, β). Associated with the boundary condition on the free surface, the integrand of the Fourier representation contains a denominator called dispersion functionD . Through the asymptotic analysis performed by Noblesse and Chen[9], the free-surface Green function can be decomposed into a local component, which is non-oscillatory and evanescent, and the wave component. The wave component which is dominant in the far field can be expressed by a single integral along the dispersion curves defined by the zeroes of the dispersion function[9]

Two typical wave patterns including V-shaped waves (inner and outer V waves) and ring waves contained in PS are depicted in Fig.2. The relationship between the dispersion curve on the Fourier plane and the associated waves on the free surface has been established by applying the method of stationary phase to the dispersion function[10]. Indeed, the wave length, and phase and group velocities are intrinsically linked to the wave number magnitude, wavenumber vector and normal vector along the dispersion curve. The crestlines (at constant-phases) of waves can then be easily obtained. Furthermore, the cusp angles are determined by the normal direction at the inflection points of dispersion curve. Similarly, a time-domain analysis based on Laplace-Fourier transform gives PS by a single Fourier integral associated with an impulsive point perturbation.
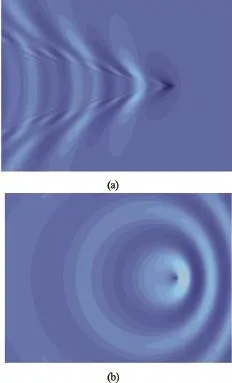
Fig.2 Typical wave patterns of PS
1.2 Body solution
Within the framework of the potential-flow theory, BS is directly obtained by the boundary integral equation which is expressed as

In Eq.(2),S denotes all boundary surfaces of the fluid domain including: body surfaceH , free surface F, the surface at infinity S∞and bottom of the water domainB. In addition,Grepresents the fundamental solution to the Laplace equation and it can be either Rankine source function in the form of1/r or the free-surface Green function satisfying all boundary conditions except that on the body surface. Here, we adopt the free-surface Green function as the fundamental solution, and then the boundary integral equation can be reduced to an integral over the body surfaceH (and the waterlineWif the forward speed effect is accounted for). On the right side of Eq.(2), the expression ∂φ /∂n is often given by the body boundary condition. As a consequence, the Eq.(2) is an integral equation with respect to φ.
In order to determine the distribution of the velocity potential over the hull surface, we first discretize the body surface into panels. If we assume the velocity potential is uniformly distributed over each panel (namely: constant BEM), the number of unknowns is equal to the number of panels, and the collocation point would locate at the geometrical center of each panel. Suppose that the body surface is discretized into N panels, and thus there areNunknowns to be determined. By imposing the boundary integral Eq.(2) on each collocation point, we haveNlinear equations. Therefore, the velocity potential on each panel can be determined by solving the resultant linear equation system. Then, the linear wave loads including the added mass and damping associated with the radiation force as well as the exiting force can be calculated following Bernoulli’s equation. Therefore, BS is essentially a linear superposition of PS, and it requires the integration of the free-surface Green function over a panel or a line segment. For the wave radiation and diffraction problems, BS is easily achieved by integrating PS over the discretized panels. Unfortunately, BS fails to be obtained when the forward speed effect is accounted for.
1.3 Point solution v.s. body solution
The far-field component of PS defined by Eq.(1) has been analyzed in Chen and Wu[2]by using the properties of Complex Error Function given in Abramowitz and Stegun[11]resultant from the asymptotic analysis of integration along the open dispersion curves, and the leading-order term of the wave component in Eq.(1) when both source and field points locate on the free surface takes the form[2]
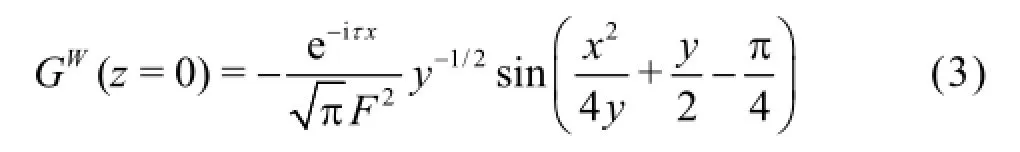
It can be shown from Eq.(3) that the free-surface Green function (PS) is highly oscillatory for a field point approaching to the track of the source point at the free surface. Depending on the path of the field point approaching to the track(y=0), PS is singular along the horizontal path and finite along any other inclined path under the free surface. The numerical evaluation of PS itself and its integration on the meshed boundary surface are very difficult, if not impossible, to obtain. In fact, the integration of Green function over a meshed panel or along a line segment giving the building block (influence coefficients) of the integral equations, inherits the similar singularity and oscillatory properties. In the limit of smaller and smaller panels (shorter and shorter segment), the integral equation should be more ill-conditioned and could not produce correct and convergent results.
BS should be totally different or at the least the leading terms (singularities and high oscillations) might be cancelled out due to destructive interference effect in the integration of PS according to Lamb[3]. Indeed, the analysis by Doutreleau and Chen[12]shows that the waterline integral involved in the boundary element integral equation is well finite. Besides, thereexist a critical frequency for the ship-motion Green function at t= Uω/ g=0.25, and PS is singular at the critical frequency. However, the work by Liu and Yue[13]showed that BS is well finite at this critical frequency and that the results (added mass, damping and wave loading) are continuous across the frequency (not critical at all in fact). Other examples include the waves in the trapping modes[14]and cloaking[15]studies where the properties of BS are totally different from those of PS. Especially for the cloaking, far-field waves are totally invisible to observers in contrary to the features of PS. In addition, the half-angle of the ship wave wedge called “Kelvin angle” is 19.47oindependent of ship’s speed obtained from the analysis of PS. However, the recent interesting works on ship wakes show that the wedge angle of wave crests behind the ship is narrower than Kelvin angle and varies with the ship speed in contrary to the Kelvin’s theory[16]. Noblesse et al.[17]expounded this phenomenon by introducing a source and a sink at the bow and stern and indicated that this is a consequence of the interference of PS.
Therefore, PS (free-surface Green function) is not directly useful. Its usefulness should be embedded in the boundary integrals which construct the basis of BEM. However, the numerical evaluation of PS and its integration on the meshed boundary surface are very difficult, if not impossible, to obtain. In fact, the integration of PS over a meshed panel or along a line segment constructing the building block (influence coefficients) of the integral equations, inherits the similar singularity and oscillatory properties. In the limit of smaller and smaller panels (shorter and shorter segment), the integral equation should be more and more ill-conditioned and could not produce correct and convergent results. As mentioned above, BS can be totally different from PS so that PS cannot be used in the usual way in which PS is first evaluated and then integrated over a discretized panel (and along a line segment).
2. Multi-domain method

In order to overcome difficulties caused by the singular and highly-oscillatory behaviors of PS, we first consider a body with smooth hull surface such as a hemi-ellipsoid, a hemi-sphere, a truncated vertical cylinder with bottom or an infinite vertical cylinder in deepwater. In the case of an infinite vertical cylinder as illustrated in Fig.3, we can write the velocity potential and its radial derivative by an expansion composed of Fourier series in polar angle and Laguerre function in vertical direction The influence coefficients in the integral equation are then associated with all elementary Fourier-Laguerre distribution and represented by six-fold integrations including the double integration on the control surface of the Green function (represented by a double Fourier integral) and the double integral following Galerkin collocation. The six-fold integrals have been analytically calculated and reduced to single integrals in wavenumber. Furthermore, the single wavenumber integrals could be evaluated semi-analytically and approximated by Chebyshev polynomials to ensure efficiency and accuracy. BS is then decomposed into a series of ES which are a smooth distribution of PS and evaluated in an analytical way. Unlike PS, these ES have similar behavior with BS since the singularity and oscillation of leading-order terms in PS are just removed and canceled out by the integration of a smooth distribution over a smooth space.
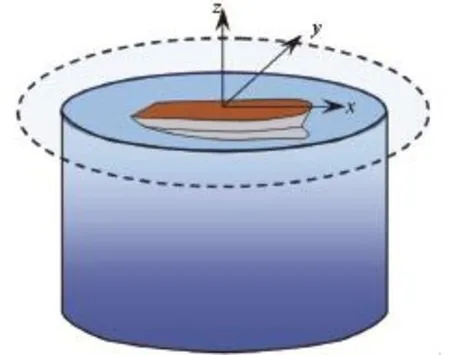
Fig.3 A ship surrounded by a control surface
For a floating body with an arbitrary geometry, we consider a control surface of analytical forms as mentioned above which surrounds the body and is at some distance. In the external domain from the control surface, the free-surface Green function satisfying the boundary condition on the free surface is used while in the internal domain limited by the control surface, the body surface and portion of free surface in between, the Rankine source function1/ris adopted. Unlike classical methods, the free-surface Green function is not explicitly evaluated but its integration on the control surface is computed analytically. ES of the external domain give the relationship between the velocity potential and its normal derivative often called the Dirichlet-to-Neumannoperator. Thisoperator will be used in establishing integral equation in the internal domain which is expressed as[5]
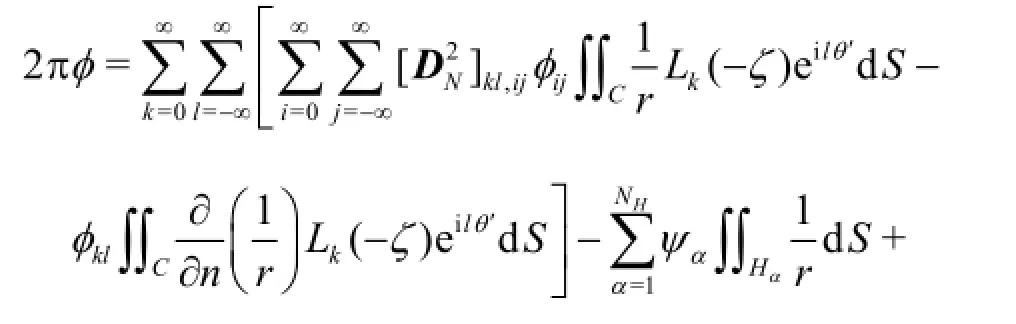

where aandβdenote the panel indices on the body surface and free surface, respectively, andk0represents the wavenumber. As a consequence, we can obtain a linear equation system with unknowns including the potential on the body surfaceφa, potential on the free surface φβand expansion coefficients on the control surface φkl.
3. Conclusion
The development of a new multi-domain method presented here takes the benefit of comprehensive understanding of wavy properties of free-surface flows. The analysis on PS vs BS has conducted us to construct appropriate ES associated with analytical distribution of unknowns on the analytical control surface. The resultant ES in the external domain construct a relationship between the velocity potential and its normal derivatives. Thisoperator can be considered as a somewhat radiation condition which closes the problem in the internal domain and provides the essential building block for the consistent and accurate solutions to the wave radiation diffraction around stationary bodies and advancing bodies with forward speed.
[1] Chen X. B. Hydrodynamics in offshore and naval applications [C]. Keynote Lecture at Proceedings 6th International Conference on Hydrodynamics. Perth, Australia, 2004.
[2] Chen X. B, Wu G. X. On singular and highly oscillatory properties of the Green function for ship motions [J]. Journal of Fluid Mechanics, 2001, 445: 77-91.
[3] Lamb H. Hydrodynamics [M]. New York, USA: Dover Publications, 1932.
[4] Ten I., Chen X. B. A coupled Rankine-Green function method applied to the forward-speed seakeeping problem [C]. Proceedings 25th International Workshop on Water Waves and Floating Bodies. Harbin, China, 2010, 165-168.
[5] Liang H., Chen X. B. A multi-domain method for the computation of wave loads [C]. Proceedings 31st International Workshop on Water Waves and Floating Bodies. Michigan, USA, 2016, 97-100.
[6] Chen X. B., Li R. P., Cheng L. Waves generated by an impulsive perturbation on vertical cylinder [C]. Proceedings 31st International Workshop on Water Waves and Floating Bodies. Michigan, USA, 2016, 21-24.
[7] Nakos D. E., Sclavounos P. D. On steady and unsteady ship wave patterns [J]. Journal of Fluid Mechanics, 1990, 215: 263-288.
[8] Wehausen J. V., Laitone E. V. Surface waves [M]. Berlin, Heidelberg, Germany: Springer-Verlag, 1960, 446-778.
[9] Noblesse F., Chen X. B. Decomposition of free-surface effects into wave and near-field components [J]. Ship Technology Research, 1995, 42: 167-185.
[10] Chen X. B., Noblesse F. Dispersion relation and far-field waves [C]. Proceedings of 12th International Workshop on Water Waves and Floating Bodies. Marseille, France, 1997, 31-35.
[11] Abramowitz M., Stegun I. A. Handbook of mathematical functions: With formulas, graphs, and mathematical tables [M]. National Bureau of Standards, 1964.
[12] Doutreleau Y., Chen X. B. Line integrals on the free surface in ship-motion problems [C]. Proceedings of 14th International Workshop on Water Waves and Floating Bodies. Port Huron, Michigan, USA, 1999, 33-36.
[13] Liu Y., Yue D. K. P. On the solution near the critical frequency for an oscillating and translating body in or near a free surface [J]. Journal of Fluid Mechanics, 1993, 254: 251-266.
[14] McIver P., McIver M. Trapped modes in the water-wave problem for a freely floating structure [J]. Journal of Fluid Mechanics, 2006, 558: 53-67.
[15] Porter R., Newman J. N. Cloaking of a vertical cylinder in waves using variable bathymetry [J]. Journal of Fluid Mechanics, 2014, 750: 124-143.
[16] Dias F. Ship waves and Kelvin [J]. Journal of Fluid Mechanics, 2014, 746: 1-4.
[17] Noblesse F., He J, Zhu Y. et al. Why can ship wakes appear narrower than Kelvin’s angle? [J]. European Journal of Mechanics-B/Fluids, 2014, 46: 164-171.
(Received June 24, 2016, Revised August 14, 2016)
* Biography:Xiaobo CHEN, Male, Ph. D., Director
- 水动力学研究与进展 B辑的其它文章
- Development of an adaptive Kalman filter-based storm tide forecasting model*
- Numerical study on the effects of progressive gravity waves on turbulence*
- Experimental tomographic methods for analysing flow dynamics of gas-oilwater flows in horizontal pipeline*
- Energy saving by using asymmetric aftbodies for merchant ships-design methodology, numerical simulation and validation*
- Coupling of the flow field and the purification efficiency in root system region of ecological floating bed under different hydrodynamic conditions*
- Modelling hydrodynamic processes in tidal stream energy extraction*

