On the nanoparticulate flow*

Jian-zhong LIN (林建忠), Ming-Zhou YU (于明州), De-ming NIE (聂德明)

1. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China

2. Institute of Fluid Measurement and Simulation, China Jiliang University, Hangzhou 310018, China,

E-mail: mecjzlin@public.zju.edu.cn

On the nanoparticulate flow*

Jian-zhong LIN (林建忠)1,2, Ming-Zhou YU (于明州)2, De-ming NIE (聂德明)2

1. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China

2. Institute of Fluid Measurement and Simulation, China Jiliang University, Hangzhou 310018, China,

E-mail: mecjzlin@public.zju.edu.cn

Nanoparticulate flows occur in a wide range of natural and engineering applications hence have received much attention. The purpose of the present paper is to provide a brief review on the research on the nanoparticulate flow in some aspects which consist of the method of moment for solving the particle population balance equation, penetration efficiency, pressure drop and heat transfer in the turbulent nanoparticulate pipe flow, fluctuating-lattice Boltzmann model for Brownian motion of nanoparticles.

nanoparticulate flow, numerical method, flow and heat transfer property, fluctuating-lattice Boltzmann, review

Introduction

Nanoparticulate flow, defined as dispersed particulate flow in which the particle size is below 1µm in diameter, occurs in a wide range of natural phenomena and industrial applications, for example, nanoparticle synthesis, contamination control in the microelectronics and pharmaceuticals industries, and diesel particulate formation. These particles with sizes much less than Kolmogorov length scale exhibit Brownian motion, and thus have different mechanism of dispersion in flows from those particles with larger size. The research on the nanoparticulate flow is required not only to know the interaction between the dispersed particles and the carrier phase, but also to understand the fundamentals of internal processes such as nucleation, condensation, coagulation and breakage.

1. Method of moment for solving particle population balance equation

In the nanoparticulate flow system the governing equation for dispersed particles is called convection-diffusion transport equation which, however, can’t provide the information of some key parameters such as particle size, number concentration, and the spectrum of particle size distribution. In order to break through this limit, Smoluchowski[1]put forward the mean-field theory. A key accomplishment of this theory is to establish the population balance equation (PBE) or particle general dynamic equation. However, the numerical solution of the PBE remains an unsolved issue now. Given the coupling between the PBE and Navier-Stokes equation for investigating nanoparticle dynamics in turbulent flows, the method of moment (MOM) became the mostly suitable method for solving the PBE in the nanoparticulate flow. Since the first MOM proposed by Hulburt and Katz[2], five predominate MOM, including the predefined size distributed method such as log-normal MOM and Gamma MOM, Gaussian quadrature MOM and its variants,pthorder-polynomial MOM, MOM with interpolative closure, and Taylor-series-expansion MOM (TEMOM), have been proposed by different researchers. Here the TEMOM will be briefly reviewed.

Since its first introduction in 2008 for solving the PBE for Brownian coagulation[3], the TEMOM has been developed further, resulting in the method being placed on a more rigorous mathematical basis and being simplified for practical application. The TEMOM was first designed to solve the PBE for spherical nanoparticles, and later, it was successfully extended to solve the PBE for the Brownian coagulationof fractal-like agglomerates. The scope of application has been extended from limited size regimes to all size regimes[4,5]. This method has also been used successfully to solve the PBE for turbulent coagulation and breakage resulting from turbulent shear force[6]. Because of the simplicity of its mathematical structure and absence of size distribution assumptions, the TEMOM was verified appropriate for achieving asymptotic solutions for PBEs[7,8]and can be used to study the self-preserving property of a nanoparticles. The TEMOM has also been confirmed to be an ideal method for solving PBEs analytically. Thus, it enables studying the time evolution of a nanoparticle analytically[9,10]. To construct TEMOM model insensitive to the coagulation kernel, the direct Taylor-series-expansion method of moment (DTMM) was proposed[11,12]. Recently, the TEMOM was further developed to meet a more general requirement for arbitrary order of Taylor-series expansion and arbitrary basis moment sequence[13]. In addition, the TEMOM has been successfully used for solving multiple dynamic problems[14,15]and multiple-mode problems[16]. When nanoparticulate dynamics is considered in a turbulent flow, the TEMOM offers the advantage of coupling the PBE with CFD because of its simple mathematical structure and properties of a typical transport equation[17,18]. As a statistical method for obtaining the ensemble properties of a system by ignoring specific details, the TEMOM’s fundamentals as well as feasibility in mathematics and statistical physics have been thoroughly studied[19].

For any MOM, the key point is to convert the PBE into a system of ordinary differential equations (ODEs) with respect to moment mk. Moment conversion involves multiplying the PBE byvkand then integrating it from 0 to∞. Unfortunately, some unexpected moments, including both fractal and integer moments, will appear, which needs to be further approximated by suitable closure models. Without loss of generality, we select the Smoluchowski equation (SE) involving only Brownian coagulation in the continuum regime as an example here. Once the SE was converted from size-dependent space to moment-dependent space using the following definition

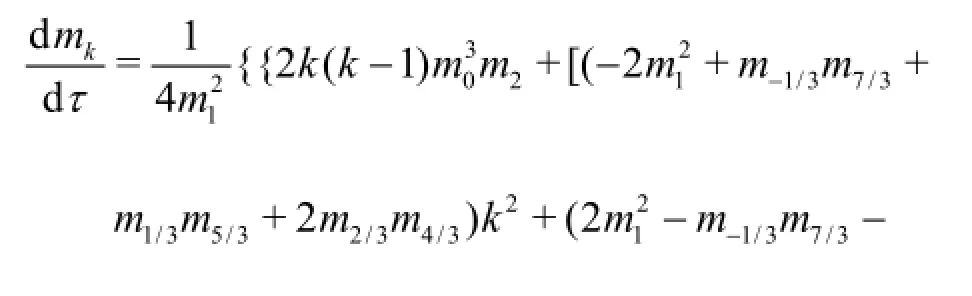
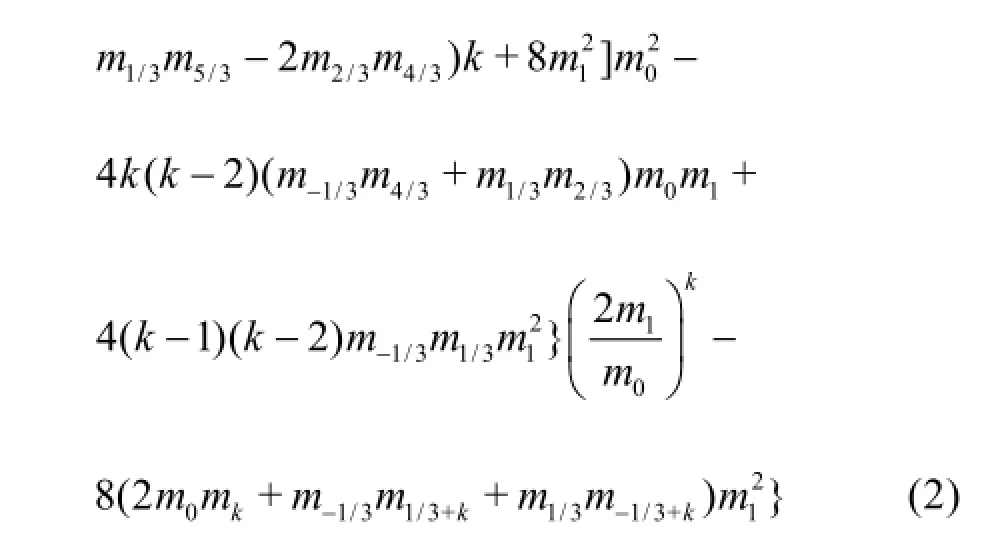
the following expression for the k-thmoment can be obtained herek can be selected to have an arbitrary value, not only integers. Equation (2) is a basic equation for moment of any order. Oncek is specified according to requirements, including those regarding the number of equations that must be solved and the type of moment sequence that should be selected, the final system of O DEs for moment can be determined.In the first version of the TEMOM[3], the basic closure equations for arbitrary moment are:

(1) The third-order Taylor-series expansion

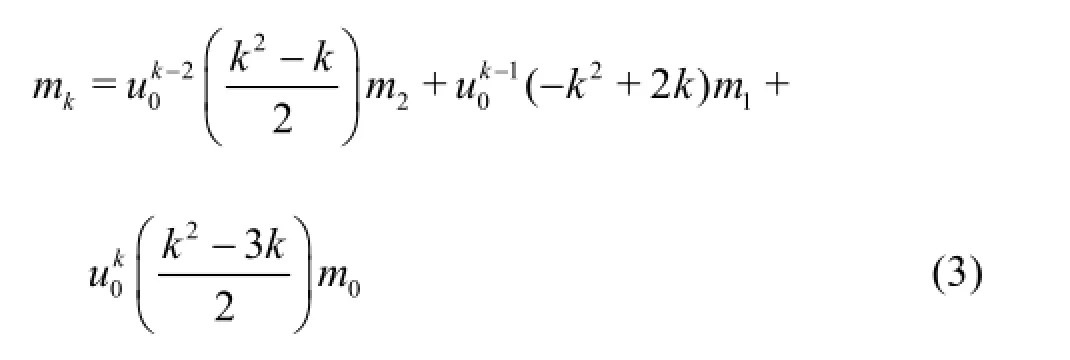
(2) The fourth-order Taylor-series expansion[20]

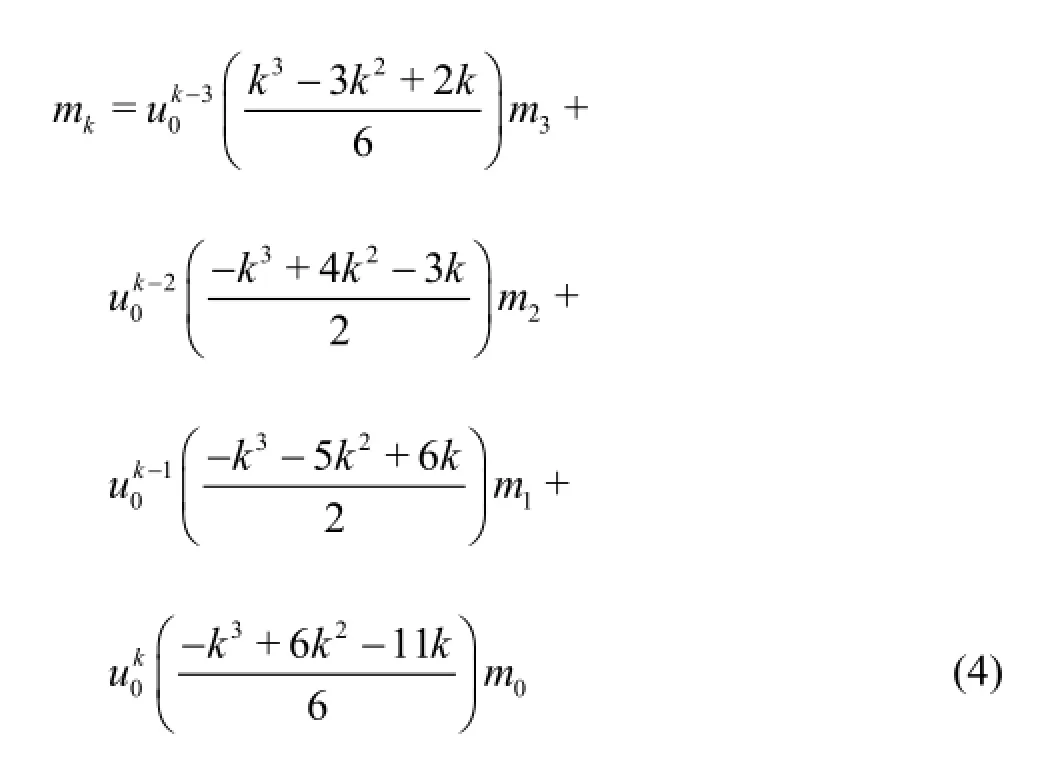
In this version, the number of ODEs is equal to the order of Taylor-series expansion. In the new version of the TEMOM, i.e. generalized TEMOM or GTEMOM[18], the basic closure equation takes the following form

where The term on the left hand side of Eq.(5) can be easily integrated out. Once integrated out, Equation (5) is the closure function for arbitrary moment and can be used to close Eq.(2). Obviously,mk/φis a function of both φandk. Equation (5) will reduce to Eqs.(3) or (4) ifφ=1. The advantage of Eq.(5) is that it can be expressed as a function of fractional moment, not only integer moment, making the TEMOM more reliable and higher accuracy. In the new version of the TEMOM, a critical variable, i.e., the Taylor-seriesexpansion point q0, should be defined in terms of φ

The generalized TEMOM was found to have two advantages over the classic TEMOM. First, the accuracy of moment, especially the fractional moment, is significantly improved, second, the scope of application according to the geometric standard deviation of the number distribution become wider. Figure 1 shows the comparison of the zero-th moment calculated with different MOM for solving Smoluchowski equation. Accordingly, the GTEMOM is recommended as an ideal method for solving PBEs.

To summarize, the TEMOM is a standard statistical method. It can successfully predict k-thmoment with high efficiency and reliability at the cost of ignoring details of the size distribution. As an effective method, the TEMOM has been verified to be reliable in solving PBEs involving one or more processes such as Brownian coagulation, breakage, condensation, and nucleation, for each limited size regime and over the entire size regime. In addition, the TEMOM can be easily combined with the CFD to deal with the complex nanoparticulate flow.

2. Penetration efficiency and distribution of nanoparticles in pipe flow

Transport of nanoparticles through a pipe has a wide range of application. For such transportation it is significant to predict particle penetration efficiency and the size distribution. In the actual applications nanoparticles are usually transported under turbulent conditions. In such case the physical mechanisms by which nanoparticles are transported and deposited on wall surfaces are complex. Particle deposition on the wall is dependent on the Brownian diffusion, turbulent diffusion, particle inertial and gravity. Shimada et al.[21]investigated experimentally the turbulent and Brownian diffusive deposition, and found deposition velocity of monodisperse particles with diameter of 10 nm-40 nm. Mols and Oliemans[22]explored the influences of the pipe size, particle diameter and Froude number on the particle deposition. Mehrzad et al.[23]presented the particle deposition velocity by extending the sublayer model for the turbulent deposition process to cover the functions of gravity, Brownian, and lift forces. Ahmadi and Chen[24]simulated numerically the particle deposition and gave the deposition rate by including the effects of turbulent diffusion, Brownian dispersion, lift force and gravity. Parker et al.[25]per-formed the simulation of the particle deposition rates byfocusing on thefunctions of turbulence model,drag model and grid resolution. Chiouet al.[26]showedthe relationship of particle concentration and convection velocity by taking into accountof the particle transport resulting from the turbulent and Brownian diffusion, eddy impaction, particle inertia and thermophoresis. Mehel et al.[27]showed that the proposed anisotropic Langevin model can enhance the accuracy of deposition prediction in the whole range of particle inertia based on the Reynolds averaged turbulence models and particle Lagrangian tracking method. Chiou et al.[28]indicated the effects of turbulent eddy diffusivity, Brownian diffusion, turbophoresis and thermophoresis on the particle deposition velocity.

Coagulation, as a process whereby particles collide with one another and adhere to form large particles, usually occurs when particles are transported. In that case the particle size and its geometric standard deviation increased and particle number density decreased, resulting in a change of particle deposition velocity. Brockmann[29]addressed the case where the effects of both coagulation and deposition are significant and the simplifying assumption of pure coagulation or pure deposition cannot be made. Kostoglou and Karabelas[30]investigated the effects of particle coagulation on the deposition rate and on the particle size distribution by simulating the interaction between fluid dynamics and particle nucleation, growth and coagulation.Ghaffarpasandet al.[31]put forward the penetration efficiencies as a function of the particle size, Stokes number and Reynolds number by measurement. Yin et al.[32]determined the penetration efficiency of nanoparticles of sizes ranging from 5.6 nm to 560 nm in diameter as a function of the Dean number, the Schmidt number and the bend angle.

As nanoparticles grow by coagulation, particle aggregate breakage will happen. As shown above there is a lack of investigation on the nanoparticle deposition under the combined effect of turbulent diffusion, Brownian diffusion, particle coagulation and breakage. While the competition between coagulation and breakage as well as diffusion affects particle distribution and hence the deposition as well as penetration efficiency.

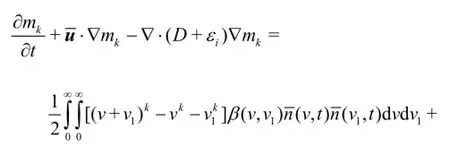
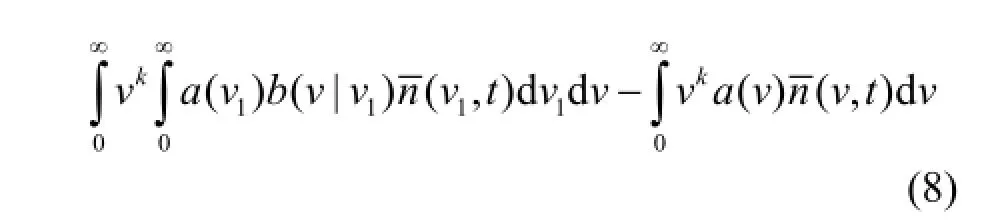
The averaged transformed moment equation for nanoparticles under the combined effect of convection, Brownian diffusion, turbulent diffusion, particle coagulation and breakage is where mis the moment,u is the fluid velocity,Dis the particle diffusion coefficient,εiis the eddy diffusivity,β(v, v1)is the volume-based coagulation kernel for two particles with volumevand v1,a( v)is the volume-based breakage kernel which gives the frequency of breakage of a particle of volumev, and b( v| v1)is the breakage distribution function.

The penetration efficiency and distribution of nanoparticles are simulated numerically for different Reynolds numbers and different ratios ofpipe length to diameter in the turbulent pipe flow[33]. Distributions of particle diameter in the cross-section are shown in Fig.2 where dpis the particle diameter,Land Dpare the length and inner diameter of the pipe. Figure 3 shows the relationship between penetration efficiency and particle diameter for different Reynolds numbers.

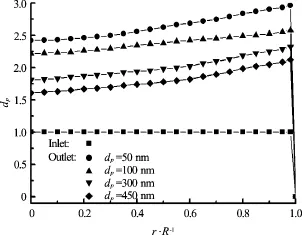
Fig.2 Distributions of particle diameter in the cross-section in the turbulent pipe flow (Re =5120,L/ d p=500)

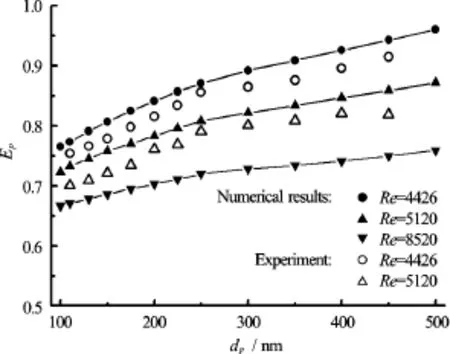
Fig.3 Relationship between penetration efficiency and particle diameter for differentRe (L/ d p=500)

The simulated results show that the particle number concentration is distributed non-uniformly in the cross-section, and the particles in the near wall region are diffused to the region near the pipe center and the wall. Particle diameter increases from an initial value at the inlet to the different values depending on the radial position at the outlet. The particles with large size are found in the near wall region from which the particle diameters decrease gradually to the pipe center. Smaller particles are easy to become more polydisperse at the outlet. The turbulent dissipation rate has a stronger effect on particle diffusion and coagulation than that on particle breakage. The larger the particles are, the larger the differences in number concentration between the region near wall and near pipe center are. 65% to 95% particles flow through the pipe. The penetration efficiencies increase with increasing particle size, while decrease as Reynolds number increases. When the pipe diameter remains unchanged, the longer the residence time of particles in the pipe is, the smaller the penetration efficiency is. Finally, the relationship of penetration efficiency and related synthetic parameters is built up based on the calculated data

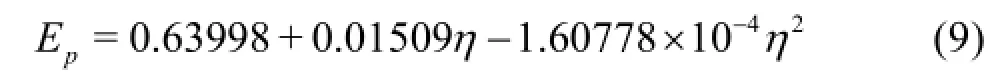
where Epis the penetration efficiency,ξ=dp/L, η= ξ×1012.

3. Pressure drop and heat transfer of nanoparticulate turbulent pipe flow

Convective heat transfer of fluid plays a significant role in the engineering applications. For increasing heat transfer, several approaches, e.g. suspending nanoparticles to fluids, have been presented. One of the most popular applications is the nanoparticulate pipe flow under turbulent conditions.

There are a large number of investigations on the pressure drop and heat transfer of nanoparticulate turbulent pipe flow. Jwo et al.[34]demonstrated that suspending Al2O3to water increases the pressure drop, and the proportional increase in the pressure drop was lower under turbulent flow conditions than under laminar flow conditions. Hao et al.[35]showed that the frictional pressured drop increases with the mass fraction of nanoparticles. Kuznetsov and Nield[36]showed that the reduced Nusselt number is a decreasing function of each of buoyancy-ratio number, Brownian motion number and thermophoresis number.Duangthongsuk and Wongwises[37]found that the heat transfer coefficient is higher than that of the base liquid and increased with increasing the Reynolds number and TiO2nanoparticle concentrations.Heyhat and Kowsary[38]indicated that the increase of the convective heat transfer could not be solely attributed to the increase of the effective thermal conductivity, and particle migration was also an important reason. Torii et al.[39]showed that the pressure loss increases slightly in comparison with that of pure water, and substantial heat transfer enhancement is caused by nanoparticles, but its effect is attenuated by large particle aggregation. Sajadi and Kazemi[40]showed that addition of small amounts of TiO2nanoparticles augmented heat transfer remarkably.

Zamzamian et al.[41]showed considerable enhancement in convective heat transfer coefficient of Al2O3and CuO/ethylene glycol, and this effect increases with increasing particles concentration and suspension temperature.Li et al.[42]indicated that the heat transfer coefficient of CuO/wateris higher than that of thebase liquid.Julia etal.[43]showed that maximum heattransfer coefficient enhancement (300%) and pressure drop penalty (1000%) of SiO2- and Al2O3/water are obtained with 5% SiO2nanofluid.Oztekinet al.[44]found that addition of spherical and elongated SiO2nanoparticles into fluids could have the potential for heat transfer enhancement without paying the penalty of increasing pumping power.Corcione et al.[45]indicated that there exists an optimal particle loading for maximum heat transfer. The optimal concentration increases as the suspension bulk temperature and the Reynolds number are increased, and the length-to-diameter ratio of the pipe is decreased, while it is independent of the nanoparticle diameter. Kayhani et al.[46]showed that heat transfer coefficients increase with increasing the TiO2/water volume fraction and it is not changed with altering the Reynolds number. The enhancement of the Nusselt number is about 8% for suspension with 2.0% nanoparticle volume fraction. Farinas Alvarino et al.[47]showed that the heat transfer enhancement by adding nanoparticles was attributed to its transport properties rather than to another transport mechanism.Prajapati and Rajvanshi[48]showed that the addition of Al2O3nanoparticles in water enhances heat transfer coefficient and the enhancement increases with increase in the nanoparticle concentration and flow rate.Bayat and Nikseresht[49]deduced that increasing the particle concentration enhances convective heat transfer rate considerably, moreover, there is a large pressure drop.Abbasian Arani and Amani[50]observed that by increasing the Reynolds number or TiO2nanoparticle volume fraction, the Nusselt number increases, by using nanofluids at high Reynolds numbers, compared with low Reynolds numbers, have lower benefits.Ziaei-Rad[51]indicated that the effect of the presence of Al2O3nanoparticles on hydraulic and thermal parameters for the turbulent flow is not very significant.Azmi et al.[52]found that the Nusselt number and friction factor at 3.0% nanofluid SiO2particle concentration are respectively greater than the values of water by 32.7% and 17.1%, the pressure drop increases with nanoparticle concentra-tion up to 3.0% and decreases thereafter.Sahin et al.[53]found that the heat transfer increased with the increase of Reynolds number and the Al2O3particle volume concentration with the exception of the particle volume concentrations of 2 and 4 vol.%.Esfe et al.[54]showed that addition of low value of MgO nanoparticles to the base fluid motivates the heat transfer to increase remarkably. The nanoparticles enhance the heat transfer without huge penalty in pumping power.

As summarized above, suspending nanoparticles to fluids can enhance heat transfer coefficient in a pipe under turbulent conditions. However, there are different conclusions on the effect of nanoparticles on the friction factor as well as pressure drop, and there have been relatively few researches on the effect of particle diameter on the properties of heat transfer and pressure drop. In addition, among the numerical studies, the distribution of particle volume concentration is usually assumed uniform without taking particle convection, diffusion, coagulation and breakage into account. Therefore, it is needed to clarify the effect of nanoparticles on the heat transfer and the pressure drop characteristics when the distribution of particle volume concentration is non-uniform, and to further assess the effect of particle diameter and volume concentration on the heat transfer and the pressure drop characteristics[55].

The nanoparticulate flow is considered as incompressible and fully developed turbulent at the exit of the pipe. The governing equations are:

where ui,p,T,ρnfand νnfare the mean velocity, pressure, temperature, effective density and effective kinematic viscosity of the suspensions, respectively,Cnfis thermal diffusivity coefficient,CT=(k is turbulent kinetic energy,εis turbulent dissipation rate,Cµ=0.09and turbulent Prandtl numberis eddy thermal diffusivity coefficient. The equation for nanoparticles is shown in Eq.(8).

The finite-volume method is used to solve the equations. The power-law scheme is selected to discretize the convection term and the SIMPLE scheme is employed to deal with the term of velocity-pressure coupling. The power-law scheme is a piece-wise approximation to the exact solution of convection-diffusion type of equation. A staggered mesh system and an alternating direction implicit method are used to solve the discretized equations. Figure 4 shows the relationship between friction factor and Reynolds number for three different particle volume concentrationsΦand pure water. The experimental results performed by Sahin et al.[53]are also given. Figure 5 shows the relationships between Nusselt number and Reynolds number for four different particle diameters.

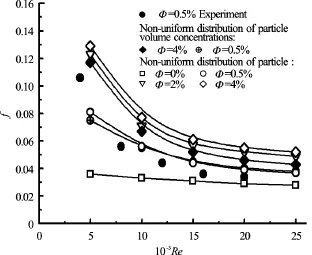
Fig.4 Friction factor vs Re for different Φ(d p=30 nm)

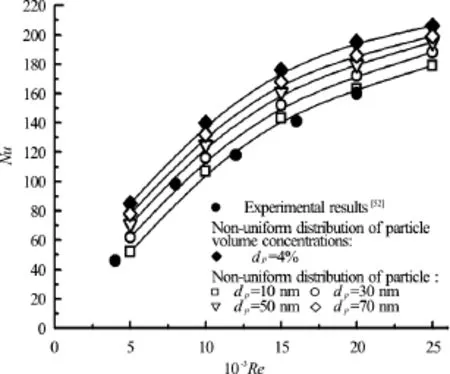
Fig.5 Nusselt number vsRe for different dp(Φ =0.5%)

The results show that friction factors increase with the increase of particle volume concentrations and particle diameter, and with the decrease of the Reynolds number. The friction factors increase remarkably at lower volume concentration, while slightly at higher volume concentration. For a fixed particle volume concentration, the friction factor is smaller for the case with the assumption that the distribution of particle volume concentration is uniform in the flow, than that the distribution is non-uniform due to the particle convection, diffusion, coagulation and breakage. The presence of nanoparticles provides higher heat transfer than pure water. The Nusselt number of suspensionsincreases with increasing the Reynolds number, particle volume concentration and particle diameter. The rate increase in Nusselt number at lower particle volume concentration is more than that at higher concentration. The heat transfer enhancement caused by the increase of Reynolds number and particle advection rate in heat transfer is of much greater magnitude than the increased surface area effect of smaller particles. For a fixed particle volume concentration, the Nusselt number is larger for the case with the assumption that the distribution of particle volume concentration is uniform in the flow, than that the distribution is non-uniform. In order to effectively enhance the heat transfer by adding nanoparticles and simultaneouslysave energy, it is necessary to make the particle distribution more uniform. Finally, the expressions of friction factor and Nusselt number as a function of particle volume concentration, particle diameter and Reynolds number are derived based on the numerical data:

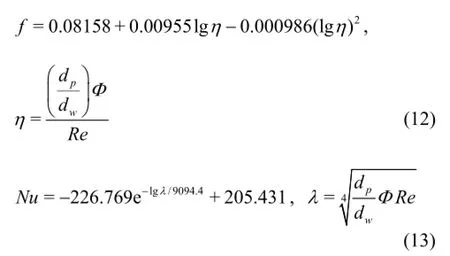
where dpand dware the diameter of particle and water molecule, respectively,Φis the particle concentration.

4. Fluctuating-lattice Boltzmann model for Brownian motion

Nanoparticles suspended in fluids experience a random force due to the thermal fluctuations in the fluid around them in addition to the average hydrodynamic force, and show Brownian motion. For many applications in chemical and biological analysis, the ability to control and measure temperature in the microfluidic devices is critical since the biological or chemical processes are dependent on temperature. Recent researches[56]demonstrate that the well-defined temperature dependence of the Brownian motion of nanoparticles could be used to present a temperature measurement technique which offers several benefits over existing methodologies. Brownian particle can be adopted to measure the local viscoelastic response of soft materials or the topography of a surrounding polymer network[57]. The motion of a Brownian probe can also be used to characterize mechanical properties of molecular motors by analyzing the particle’s trajectory[58]. Moreover, the biased Brownian motions or rectified Brownian motions, induced by an energy source[59]or by broken spatial reflection symmetry[60], provide a very effective technique for particle separation. Furthermore, it has been demonstrated[61]that nanoparticles in a conventional base fluid, known as nanofluids, tremendously enhance the heat transfer characteristics of the original fluid. At the same time, some researchers[62,63]have declared that Brownian motion is a key mechanism governing the thermal behavior of nanofluids. Due to its importance in engineering applications, there has always been a great deal of interest in developing algorithms that can provide a better understanding of particle’s Brownian motion. Especially in some cases where high resolution of Brownian motion is needed, the numerical algorithms are required to observe the motion on short time scalesMis particle mass,a is particle radius,µis fluid viscosity,Jis moment of inertia).

Roughly speaking, the existing numerical methods for modeling particle’s Brownian motion can be categorized by the treatment of particle’s motion equations into two groups. (1) The method based on Langevin type equation. Brownian dynamics (BD)[64]and Stokes dynamics (SD)[65]are the most important methods in this group. These methods treat the particle’s motion based on the Langevin equations without treatment of the fluid flow, which indicates that random fluctuations are applied directly into the particles. The approximate expressions and the Rotne-Prager-Yamakawa tensors are used to model the hydrodynamic interactions for BD and SD, respectively. BD and SD are widely and effectively used to simulate the particles’ Brownian motion. One of major defects of the method based on Langevin type equation may be that it cannot account for the short-time motion of Brownian particle[66]and cannot deal with the Brownian motion of non-spherical particles. (2) Direct numerical simulation method(DNS). In this group, the thermal fluctuations in the fluid, which result in the Brownian motion of particles, are modeled by adding a random stress tensor to Navier-Stokes equations. This method was called fluctuating hydrodynamics[67]. The Brownian motion of particles can be described by solving the fluctuating hydrodynamic equations coupled with the equations of particle motion. In this method, the particles acquire random motion through the hydrodynamic force acting on its surface from the surrounding fluctuating fluid. Therefore, there is no need to add a random force term in the particles’ equations, unlike Langevin equations. Sharma and Patankar[68]have solved the fluctuating hydrodynamic equations through finite volume method and their numerical results include the Brownian displacements of a spherical particle and drag coefficient acting on the particle,which agree well with the analytic values. This method can successfully account for the short-time motion and deal with the particles of irregular shape in a straightforward manner. In the late 1990’s Ahlrichs and Dünweg[69]applied the fluctuating lattice Boltzmann equations to simulate the polymer solutions successfully. Meanwhile, it should be stated that a random stress tensor required for a spatial grid needs a lot of random numbers for the fluctuating hydrodynamics, especially in the three-dimensional simulations.

Fig.6Root mean square values of velocity and angular velocity for a elliptical particle with Brownian motion

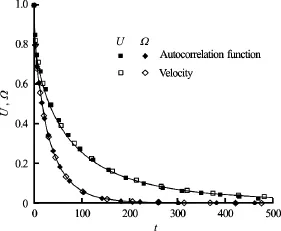
Fig.7 Correlation function of velocity and angular velocity for a elliptical particle with Brownian motion

In general, the main obstacle of the fluctuating hydrodynamics is to solve Navier-Stokes equation, which is usually a very complicated task, especially in the three-dimensional flows. As an alternative computational technique to the Navier-Stokes solvers, lattice-Boltzmann method (LBM) has achieved a great success in simulating particle suspensions in the past decades[70,71], demonstrating that LBM is a promising numerical scheme for multi-component fluid flow. Application of LBM coupled with fluctuating hydrodynamics to simulate particle’s Brownian motion was first proposed by Ladd[66], which is performed by adding a fluctuating term in the two-relaxation-time (TRT) LB equations. The same idea is adopted to establish a single-relaxation-time (SRT) fluctuating LB model[72], which is most widely used due to its high computational efficiency. By performing a Chapman-Enskog expansion the continuum and Navier-Stokes equations can be recovered from LB equations, proving that the fluctuating term is equivalent to the random stress tensor in fluctuating hydrodynamic equations. As a validation of the present fluctuating LB model, a threedimensional implementation for D3Q15 lattice has been presented. The equation for fluid in the fluctuating LB mode is

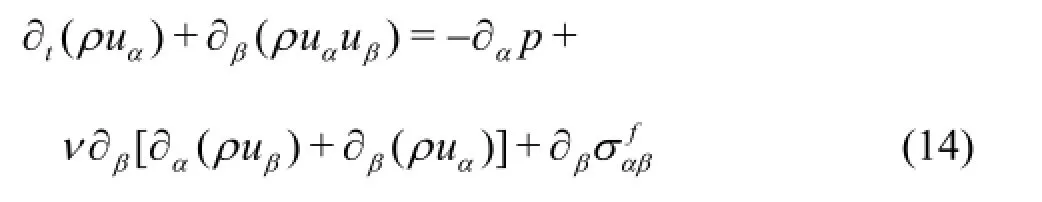
the last term on the right hand side of Eq.(8) is the random stress tensor which reflects the molecular thermal fluctuations. Based on Eq.(14), the Brownian motion of nanoparticles can be simulated. Figures 6 and 7 show the root mean square values and correlation functions of velocity and angular velocity for a elliptical particle with Brownian motion.

[1] Smoluchowski M. von. Versuch einer mathematischen theorie der Koagulationskinetik kolloider Losungen [J]. Zeitschrift Für Physikalische Chemie, 1917, 92: 129-168.

[2] Hulburt H. M., Katz S. Some problems in particle technology: A statistical mechanical formulation [J]. Chemical Engineering Science, 1964, 19(8): 555-574.

[3] Yu M. Z., Lin J. Z., Chan T. L. A new moment method for solving the coagulation equation for particles in Brownian motion [J]. Aerosol Science and Technology, 2008, 42(9): 705-713.

[4] Yu M. Z., Lin J. Z. Solution of the agglomerate Brownian coagulation using Taylor-expansion moment method [J]. Journal of Colloid and Interface Science, 2009, 336(1): 142-149.

[5] Yu M. Z., Lin J. Z. Taylor-expansion moment method for agglomerate coagulation due to Brownian motion in the entire size regime [J]. Journal of Aerosol Science, 2009, 40(6): 549-562.

[6] Yu M. Z., Zhang K. The verification of the Taylor-expansion moment method in solving aerosol breakage [J]. Thermal Science, 2012, 16(5): 1424-1428.

[7] Chen Z. L., Lin J. Z., Yu M. Z. Asymptotic behavior of the Taylor-expansion method of moments for solving a coagulation equation for Brownian particles [J]. Particuology, 2014, 14: 124-129.

[8] Xie M. L., He Q. Asymptotic solution of population balance equation based on TEMOM model [J]. Chemical Engineering Science, 2013, 94: 79-83.

[9] Xie M. L., He Q. Analytical solution of TEMOM model for particle population balance equation due to Brownian coagulation [J]. Journal of Aerosol Science, 2013, 66: 24-30.

[10] Yu M. Z., Zhang X., Jin G. D. et al. A new analytical solution for solving the population balance equation in the continuum-slip regime [J]. Journal of Aerosol Science, 2015, 80: 1-10.

[11] Chen Z. L., Lin J. Z., Yu M. Z. A direct expansion method of moments for Brownian coagulation [J]. Physica Scripta, 2014, 89(12): 125204.

[12] Yuan F. Y., Chen Z. L. Direct expansion method of moments with n/3th moments for nanoparticle Brownian coagulation in the free molecule regime [J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2014, 25(1): 1-12.

[13] Yu M. Z., Liu Y. Y., Lin J. Z. et al. Generalized TEMOM scheme for solving the population balance equation [J]. Aerosol Science and Technology, 2015, 49(11): 1021-1036.

[14] Yu M. Z., Lin J. Z. Nanoparticle-laden flows via moment method: A review [J]. International Journal of Multiphase Flow, 2010, 36(2): 144-151.

[15] Yu M. Z., Lin J. Z., Chan T. L. Numerical simulation for nucleated vehicle exhaust particulate matters via the TEMOM/LES method [J]. International Journal of Modern Physics C, 2009, 20(3): 399-421.

[16] Yu M. Z., Seipenbusch M., Yang J. et al. A new analytical solution for solving the smoluchowski equation due to nanoparticle Brownian coagulation for non-self-preserving system [J]. Aerosol and Air Quality Research, 2014, 14(6): 1726-1737.

[17] Xie M. L., Yu M. Z., Wang L. P. A TEMOM model to simulate nanoparticle growth in the temporal mixing layer due to Brownian coagulation [J]. Journal of Aerosol Science, 2012, 54(12): 32-48.

[18] Xie M. L., Yu M. Z., Wang L. P. A TEMOM model to simulate nanoparticle growth in the temporal mixing layer due to Brownian coagulation [J]. Journal of Aerosol Science, 2012, 54(12): 32-48.

[19] Xie M. L., He Q. The fundamental aspects of TEMOM model for particle coagulation due to Brownian motion. Part I: In the free molecule regimes [J]. International Journal of Heat and Mass Transfer, 2014, 70(3): 1115-1120.

[20] Zhang X., Yu M. Z., Liu Y. Y. et al. Verification of expansion orders of the Taylor-Series expansion method of moment model for solving population balance equations [J]. Aerosol and Air Quality Resarch, 2015, 15: 2475-2484.

[21] Shimada M., Okuyama K., Asai M.Deposition of submicron aerosol-particles in turbulent and transitional flow[J]. AIChE Journal, 1993, 39(1): 17-26.

[22] Mols B., Oliemans R. V. A.A turbulent diffusion model for particle dispersion and deposition in horizontal tube flow[J]. International Journal of Multiphase Flow, 1998, 24(1): 55-75.

[23] Mehrzad S., Goodarz A., Hasan R. A sublayer model for deposition of nano- and micro-particles in turbulent flows [J]. Chemical Engineering Science, 2000, 55(24): 6097-6107.

[24] Ahmadi G., Chen Q.Numerical simulation of particle transport and dispersion in turbulent pipe flows[J]. Review of Educational Research, 2001, 25(2): 77-84.

[25] Parker S., Foat T., Preston S.Towards quantitative prediction of aerosol deposition from turbulent flows[J]. Journal of Aerosol Science, 2008, 39(2): 99-112.

[26] Chiou M. C., Chiu C. H., Chen H. S.Formulation for predicting deposition velocity of particles in turbulence [J]. International Journal of Thermal Sciences, 2010, 49(2): 290-301.

[27] Mehel A., Taniere A., Oesterle B. et al.The influence of an anisotropic langevin dispersion model on the prediction of micro- and nanoparticle deposition in wall-bounded turbulent flows[J]. Journal of Aerosol Science, 2010, 41(8): 729-744.

[28] Mehel A., Taniere A., Oesterle B. et al.The influence of an anisotropic langevin dispersion model on the prediction of micro- and nanoparticle deposition in wall-bounded turbulent flows[J]. Journal of Aerosol Science, 2010, 41(8): 729-744.

[29] Brockmann J. E. Coagulation and deposition of ultrafine aerosols in turbulent pipe flow [D]. Doctoral Thesis, Minneapolis, USA: University of Minnesota, 1981.

[30] Kostoglou M., Karabelas A. J.Comprehensive modeling of precipitation and fouling in turbulent pipe flow[J]. Industrial and Engineering Chemistry Research, 1998, 37(4): 1536-1550.

[31]GhaffarpasandO.,DrewnickF.,HosseiniebalamF. et al. Penetration efficiency of nanometer-sized aerosol particles in tubes under turbulent flow conditions [J]. Journal of Aerosol Science, 2012, 50(2): 11-25.

[32] Yin Z. Q., Lin J. Z., Lou M. Penetration efficiency of nanoparticles in a bend of circular cross-section [J]. Journal of Hydrodynamics, 2015, 27(1): 93-98.

[33] Lin J. Z., Yin Z. Q., Gan F. J. et al. Penetration efficiency and distribution of aerosol particles in turbulent pipe flow undergoing coagulation and breakage [J]. International Journal of Multiphase flow, 2014, 61(5): 28-36.

[34]Jwo C. S., Teng T. P., Wu D. J. et al.Research on pressure loss of alumina nanofluid flow in a pipe[J]. Journal of the Chinese Society of Mechanical Engineers, 2009, 30(6): 511-517.

[35] Hao P., Ding G. L., Jiang W. T.Measurement and correlation of frictional pressure drop of refrigerant-based nanofluid flow boiling inside a horizontal smooth tube[J]. International Journal of Refrigeration-Revue Internationale Du Froid, 2009, 32(7): 1756-1764.

[36] Kuznetsov A. V., Nield D. A.Natural convective boundary-layer flow of a nanofluid past a vertical plate[J]. International Journal of Thermal Sciences, 2010, 49(2): 243-247.

[37] Duangthongsuk W., Wongwises S.An experimental study on the heat transfer performance and pressure drop of tio2-water nanofluids flowing under a turbulent flow regime[J]. International Journal of Heat and Mass Transfer, 2010, 53(1-3): 334-344

[38] Heyhat M. M., Kowsary F.Effect of particle migration on flow and convective heat transfer of nanofluids flowing through a circular pipe[J]. Journal of Heat Transfer-Tran- sactions of the ASME, 2010, 132(6): 062401.

[39]Torii S., Satou Y., Koito Y.Experimental study on convective thermal-fluid flow transport phenomena in circular tube using nanofluids[J]. International Journal of Green Energy, 2010, 7(3): 289-299.

[40] Sajadi A. R., Kazemi M. H.Investigation of turbulent convective heat transfer and pressure drop of TiO2/water nanofluid in circular tube[J]. International Communications in Heat and Mass Transfer, 2011, 38(10): 1474-1478.

[41] Zamzamian A., Oskouie S. N., Doosthoseini A. et al. Experimental investigation of forced convective heat transfer coefficient in nanofluids of Al2O3/EG and CuO/EG in a double pipe and plate heat exchangers under turbulent flow[J]. Experimental Thermal and Fluid Science, 2011, 35(3): 495-502.

[42] Li D. D., Zhao W. L., Liu Z. M. et al.Experimental inve-stigation of heat transfer enhancement of the heat pipe using CuO-water nanofluid[J]. Advanced Materials Research, 2011, 160-162: 507-512.

[43] Julia J. E., Hernandez L., Martinez-Cuenca R. et al.Measurement and modelling of forced convective heat transfer coefficient and pressure drop of Al2O3- and SiO2-water nanofluids[J]. Journal of Physics Conference Series, 2012, 395(1): 012038.

[44] Oztekin A., Neti S., Ukaew A.Effects of nanoparticles and polymer additives in turbulent pipe flow[C]. Proceedings of the ASME International Mechanical Engineering Congress and Exposition. Vancouver, British Columbia, Canada, 2012, 9: 761-766.

[45] Corcione M., Cianfrini M., Quintino A.Heat transfer of nanofluids in turbulent pipe flow[J]. International Journal of Thermal Sciences, 2012, 56(7): 58-69.

[46] Kayhani M. H., Soltanzadeh H., Heyhat M. M. et al.Experimental study of convective heat transfer and pressure drop of TiO2/water nanofluid[J]. International Communications in Heat and Mass Transfer, 2012, 39(3): 456-462.

[47] Farinas Alvarino P., Saiz Jabardo J. M., Arce A. et al.Heat transfer enhancement in nanofluids. A numerical approach[J]. Journal of Physics Conference Series, 2012, 395(1): 012116.

[48] Prajapati O. S., Rajvanshi A. K.Al2O3-water nanofluids in convective heat transfer[J]. Applied Mechanics and Materials, 2012, 110-116: 3667-3672.

[49] Bayat J., Nikseresht A. H.Thermal performance and pressure drop analysis of nanofluids in turbulent forced convective flows[J]. International Journal of Thermal Sciences, 2012, 60(1): 236-243.

[50] Abbasian Arani A. A., Amani J.Experimental study on the effect of TiO2-water nanofluid on heat transfer and pressure drop[J]. Experimental Thermal and Fluid Science, 2012, 42(5): 107-115.

[51] Ziaei-Rad M. Numerical investigation of pressure drop and heat transfer in developing laminar and turbulent nanofluid flows [J]. Physica Scripta, 2013, T155: 014021.

[52] Azmi W. H., Sharma K. V., Sarma P. K. et al.Experimental determination of turbulent forced convection heat transfer and friction factor with SiO2nanofluid[J]. Experimental Thermal and Fluid Science, 2013, 51: 103-111.

[53] Sahin B., Gultekin G. G., Manay E. et al.Experimental investigation of heat transfer and pressure drop characteristics of Al2O3-water nanofluid[J]. Experimental Thermal and Fluid Science, 2013, 50: 21-28.

[54]Esfe M. H., Saedodin S., Mahmoodi M. Experimental studies on the convective heat transfer performance and thermophysical properties of MgO-water nanofluid under turbulent flow[J]. Experimental Thermal and Fluid Science, 2014, 52: 68-78.

[55] Lin J. Z., Xia Y., Ku X. K. Pressure drop and heat transfer of nanofluid in turbulent pipe flow considering particle coagulation and breakage [J]. Journal of Heat Transfer-Transactions of the ASME, 2014, 136(11): 111701.

[56] Chung K., Cho J. K., Park E. S. et al. Three-dimensional in situ temperature measurement in microsystems using Brownian motion of nanoparticles [J]. Analytical Chemistry, 2009, 81: 991-999.

[57] Tischer C., Altmann S., Fisinger S. et al. Three-dimensional thermal noise imaging [J]. Applied Physics Letters, 2001, 79(23): 3878-3880.

[58] Jeney S., Stelzer E. H. K., Grubmuller H. et al. Mechanical properties of single motor molecules studies by threedimensional thermal force probing in optical tweezers [J]. ChemPhysChem, 2004, 5(8): 1150-1158.

[59] Dean Astumian R. Thermodynamics and kinetics of a Brownian motor [J]. Science, 1997, 276(5314): 917-922.

[60] Derenyi I., Astumian, R. D. AC separation of particles by biased Brownian motion in a two-dimensional sieve [J]. Physical Review E, 1998, 58(6): 7781-7784.

[61] Keblinski P., Phillpot S. R., Choi S. U. S. et al. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids) [J]. International Journal of Heat and Mass Transfer, 2002, 45(4): 855-863.

[62] Rasher R., Bhattacharya P., Phelan P. E. Thermal conductivity of nanoscale colloidal solutions (nanofluids) [J]. Physical Review Letters, 2005, 94(2): 025901.

[63] Jang S. P., Choi S. U. S. Role of Brownian motion in the enhanced thermal conductivity of nanofluids [J]. Applied Physics Letters, 2004, 84(21): 4316-4318.

[64] Ermak D. L., McCammon J. A. Brownian dynamics with hydrodynamic interactions [J]. Journal of Chemical Physics, 1978, 69(4): 1352-1360.

[65] Brady J. F., Bossis G. Stokesian dynamics [J]. Annual Review of Fluid Mechanics, 1988, 20: 111-157.

[66] Ladd A. J. C. Short-time motion of colloidal particles: Numerical simulation via a fluctuating lattice-Boltzmann equation [J]. Physical Review Letters, 1993, 70(9): 1339-1342.

[67] Landau L. D., Lifshitz E. M. Fluid mechanics [M]. London, UK: Pergamon Press, 1959.

[68] Sharma N., Patankar N. A. Direct numerical simulation of the Brownian motion of particles by using fluctuating hydrodynamic equations [J]. Journal of Computational Physics, 2004, 201(2): 466-486.

[69] Ahlrichs P., Dünweg B. Simulation of a single polymer chain in solution by combining lattice Boltzmann and molecular dynamics [J]. Journal of Chemical Physics, 1999, 111(17): 8225-8239.

[70] Aidun C. K., Clausen J. R. Lattice-Boltzmann method for complex flows [J]. Annual Review of Fluid Mechanics, 2010, 42: 439-472.

[71] Shi X.,Zhang S.,Wang S. L. Numerical simulation of hemodynamic interactions of red blood cells in micro-capillary flow [J]. Journal of Hydrodynamics, 2014, 26(2): 178-186.

[72] Nie D. M., Lin J. Z. A fluctuating lattice-Boltzmann model for direct numerical simulation of particle Brownian motion [J]. Particuology, 2009, 7(6): 501-506.

(Received June 15, 2016, Revised September 5, 2016)

* Project supported by the Major Program of National Natural Science Foundation of China (Grant No. 11632016).

Biography:Jian-zhong LIN (1958-), Male, Ph. D., Professor