涡旋压缩机滑环式防自转机构的摩擦磨损研究*

刘兴旺 汪 洋

(1.兰州理工大学石油化工学院；2.兰州理工大学温州泵阀研究院)

涡旋压缩机滑环式防自转机构的摩擦磨损研究*

刘兴旺**1,2汪 洋1

(1.兰州理工大学石油化工学院；2.兰州理工大学温州泵阀研究院)

十字滑环的摩擦磨损对涡旋压缩机动静涡旋盘的精确啮合和整机的高效运行均有很大影响，为探究十字滑环的摩擦磨损特性，根据动涡旋盘和十字滑环所受力的平衡方程，推导出十字滑环凸键处所受正压力的计算方法，代入样机数据计算得到了十字滑环所受摩擦力的变化规律。利用有限元软件模拟了做变速往复运动的十字滑环的摩擦接触，分析了十字滑环的实时接触状态和摩擦力分布情况，并计算出十字滑环的摩擦损失功率。结果表明：十字滑环在动涡旋盘滑槽处受到的摩擦力随主轴转角按类似正、余弦函数规律变化，十字滑环在机架滑槽处受到的摩擦力在一个运动周期内基本不变；十字滑环与动涡旋盘接触的凸键处受力随主轴转角变化而有规律地发生改变，不断对十字滑环凸键键端处造成冲击，这是致使十字滑环容易磨损的主要原因；十字滑环摩擦应力变化显著处是十字滑环与动涡旋盘接触的凸键部位，凸键部位的键端处是十字滑环最易磨损的部位；十字滑环摩擦损失功率约为20～90W，占整机摩擦损失功率的比例约10%。

涡旋压缩机 十字滑环式防自转机构 摩擦 磨损

涡旋压缩机动涡旋盘以一个定回转半径绕静涡旋盘做公转平动,形成有效容积腔,对工作介质进行压缩。为此需设置一套防自转机构，实现动涡旋盘的公转平动。十字滑环防自转机构因具有结构简单、工艺性好、易于装配及便于润滑等特点而被广泛应用[1]。但涡旋压缩机十字滑环上的凸键与涡旋压缩机支架上的滑槽和动涡旋盘上的滑槽之间形成摩擦，极易造成摩擦副的磨损。导致动、静涡旋盘难以精确啮合，致使涡旋压缩机不能正常工作。涡旋压缩机的摩擦磨损一直是研究的热点和难点之一。

针对上述问题，周家胜介绍了6种常见的公转型涡旋流体机械防自转机构[2]，其中对十字滑环防自转机构的工作原理进行了说明，并介绍了3种已经使用的十字滑环样式。李超等以无油润滑涡旋压缩机的动、静涡旋盘端面摩擦为研究对象，分析了动、静涡旋盘端面摩擦损失，建立了动、静盘端面摩擦力学分析模型[3]。曹霞等分析了立式高压型涡旋压缩机在稳定运行工况下的摩擦副及其摩擦润滑状态[4]，对涡旋压缩机的径向轴承类摩擦副进行建模，根据涡旋压缩机的载荷和相位分布特征对载荷式进行了积分，得到了该类摩擦副在压缩机稳定运行时摩擦力的分析解。刘兴旺等分析了具有背压腔结构的基圆渐开线型立式涡旋压缩机涡盘摩擦损耗、动静涡盘间的泄漏损耗与涡盘几何参数的关系[5]。已有的研究多是对涡旋压缩机十字滑环进行力学分析，说明其工作原理。对涡旋压缩机的摩擦磨损问题研究也以动、静涡旋盘之间形成的摩擦副为研究对象。而对涡旋压缩机十字滑环摩擦磨损问题的研究则少有涉及。因此，笔者以某样机为研究对象，对其动涡旋盘、十字滑环受力进行动力学分析与计算，并利用ANSYS分析软件对做变速往复运动的十字滑环的接触状态进行模拟分析，计算出在实际工况下十字滑环的摩擦损失功率。

1 十字滑环动力学分析

笔者以一压缩机样机为算例进行分析，其参数为：吸气压力ps=0.2MPa，排气压力pd=1.46MPa，开始排气角θ*=1.778π，等熵压缩指数k=1.41，十字滑环环形中心面的直径D0=135mm，十字滑环凸键键宽B=12mm，涡旋齿高度h=40mm，动涡旋盘回转半径r=5.1mm，主轴转速n=3000r/min。

涡旋压缩机的十字滑环安装在涡旋压缩机动涡旋盘和机架之间，十字滑环上4个凸键分别嵌入到动涡旋盘端板背面滑槽和机架固定端盖滑槽中，如图1所示。十字滑环与动涡旋盘相嵌侧的凸键沿动涡旋盘端板背面滑槽做相对滑动，十字滑环另一侧的凸键沿机架上的滑槽做相对滑动。这种装配关系使得动涡旋盘相对于静涡旋盘只能做回转平动而不发生自转，正好满足动、静盘的啮合需要。

如图2所示，嵌入动涡旋盘端板背面滑槽的十字滑环凸键的相对滑动速度为ux，嵌入机架滑槽的十字滑环凸键的相对滑动速度为uy。十字滑环受到来自动涡旋盘的正压力F1、F2，来自机架的正压力F3、F4。F1～F4始终垂直作用于滑槽壁侧[6～8]。

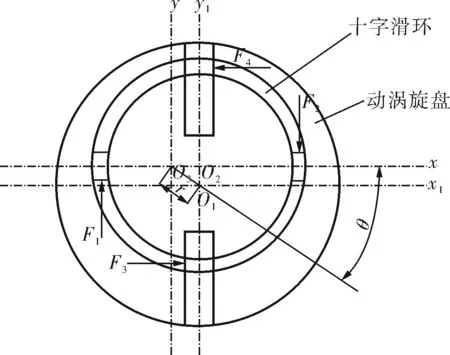
图2 十字滑环受力图

设十字滑环的z方向垂直于图2中十字滑环xy平面，x方向的受力平衡方程、y方向的受力平衡方程、z方向上的力矩平衡方程分别为：

∑Fx=0,F3-F4-μ1(F3-F4)=0

(1)

∑Fy=0,F1-F2+μ2(F3+F4)=Fm

(2)

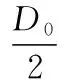
(3)

式中Fm——往复惯性力；

μ1——十字滑环与动涡旋盘间的摩擦系数；

μ2——十字滑环与机架间的摩擦系数。

动涡旋盘z方向与十字滑环z方向平行，动涡旋盘在z方向上的力矩平衡方程：

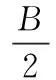
(4)

式中Mr——动涡旋盘自转力矩；

θ——主轴转角。

联立式(1)～(4)，可求解F1、F2、F3、F4。令：

(5)

(6)

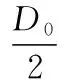
(7)

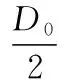
(8)

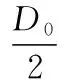
(9)

c2=Mr

(10)

则：

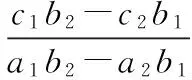
(11)

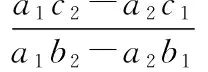
(12)

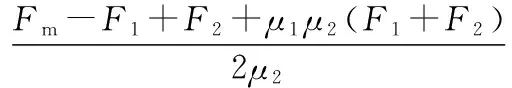
(13)

(14)

分析式(11)～(14)可知，决定F1、F2、F3、F4的大小的变量中a1、b1、a2、b2的值都比较小，F1、F2、F3、F4的大小主要受c1、c2的影响。所以自转力矩Mr和十字滑环沿支架滑槽产生的往复惯性力Fm对十字滑环上的正压力F1、F2、F3、F4的大小变化起主要作用。

代入样机参数，求得自转力矩Mr随主轴转角θ变化的曲线(图3)和十字滑环上正压力F1、F2、F3、F4随主轴转角θ变化的曲线(图4)。

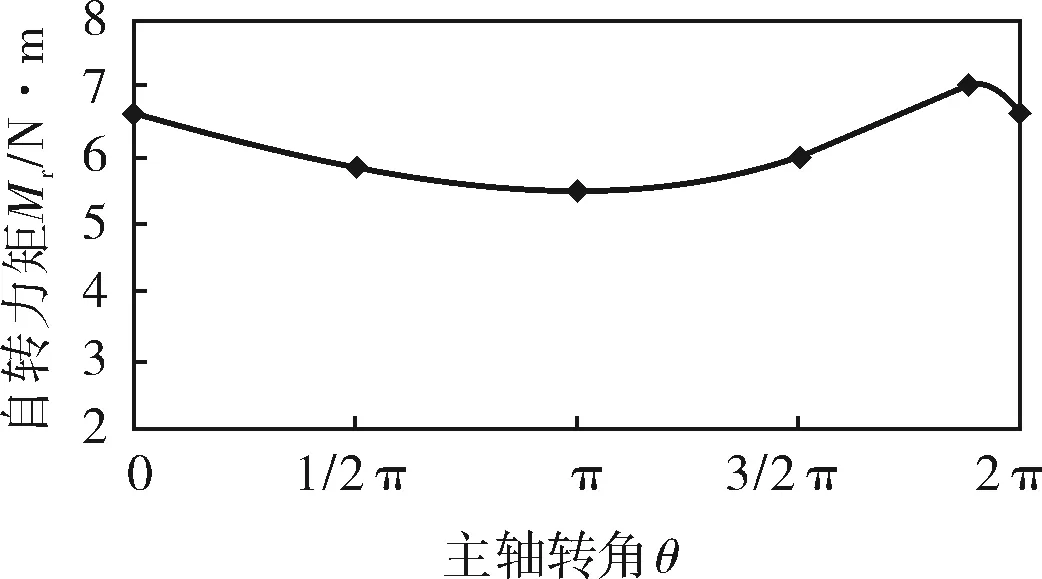
图3 自转力矩随主轴转角变化的曲线

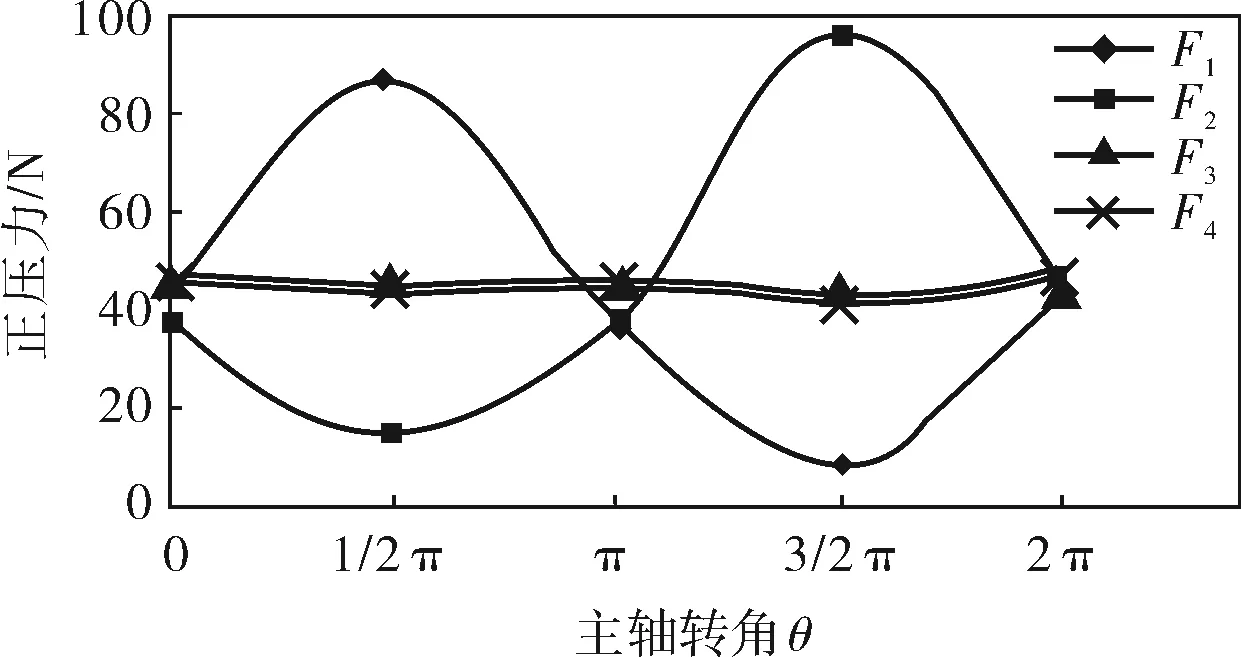
图4 十字滑环上所受正压力随主轴转角变化的曲线

如图3所示，Mr在一个周期内的变化幅度很小，对F1、F2、F3、F4的变化周期影响有限。十字滑环的往复惯性力越大，F1、F2、F3、F4的大小变化幅度就越大，引起机器的振动就越剧烈。所以在满足十字滑环强度和刚度要求的前提下，十字滑环的质量m应尽量减轻。图4中F1、F2随主轴转角以类似正、余弦函数规律变化，F3、F4是作用在压缩机支架滑槽上的力，大小在一个运动周期内基本不变。

十字滑环在动涡旋盘与机架之间往复滑动，它所受到的摩擦力即为滑动摩擦力，滑动摩擦力的大小为正压力与摩擦因数的乘积[9]。则可总结出十字滑环在动涡旋盘滑槽处受到的摩擦力随主轴转角按类似正余弦函数规律变化，十字滑环在机架滑槽处受到的摩擦力大小基本不变。

在涡旋压缩机高速运行的条件下，十字滑环同样做高速的往复运动，在这个过程中十字滑环的受力也时刻发生着变化，当其速度为零，同时改变运动方向时，十字滑环上各凸键受力基本相同；当主轴转角转到π/2、3π/2时，十字滑环与动涡旋盘接触的凸键受力最大。这导致十字滑环与动涡旋盘接触的凸键在运行过程中将不断受到高频冲击，极易损坏。

2 十字滑环接触应力的有限元分析

十字滑环摩擦、磨损的产生和摩擦表面的接触状态、接触应力密切相关，所以了解和研究摩擦表面的接触状态和接触应力是分析、解决摩擦学各种问题不可缺少的部分。

使用ANSYS有限元软件可以对十字滑环接触状态进行模拟仿真[10]。但涡旋压缩机十字滑环防自转机构做变速的往复运动，每一个时刻十字环的速度和受力都是变化的，很难模拟十字环一个周期内的接触应力变化情况。笔者模拟了十字滑环滑动速度为零时的接触状态和速度最大时的接触状态，并通过这两种特定状态分析其极限受力状态和摩擦磨损机理。

2.1模型建立

笔者先采用Solidworks软件直接建立三维实体模型，然后将模型导入ANSYS Workbench有限元软件中进行分析。模型的动涡旋盘端板平面为xy平面，动涡旋盘涡旋齿齿高方向为z方向，其结构参数为：动涡旋盘的端板半径100mm，端板滑槽与机架滑槽宽12mm，动涡旋盘的齿高40mm，十字滑环的半径75mm，环宽15mm，环高16mm，十字滑环上的凸键高8mm，凸键宽12mm。

2.2模型的物理属性及网格划分

在ANSYS Workbench中新建材料：铸造硅铝合金，密度为2.68g/cm3，弹性模量为74GPa，泊松比为0.33；灰铸铁HT250，密度7.15g/cm3，弹性模量为113GPa，泊松比为0.26；定义十字滑环的材料为铸造硅铝合金，动涡旋盘和机架的材料为灰铸铁HT250。采用网格划分中的自由网格划分方法，并使用Refinement选项对动涡旋盘滑槽处、十字滑环凸键处、机架滑槽处的网格分别进行加密。

2.3接触属性基本选项设置

ANSYS Workbench接触采用接触对的概念，接触对由目标面和接触面组成。设置十字滑环每个凸键上的3个面为目标面，与它相接触的滑槽上的3个面为接触面，同时设置十字滑环的上环面与动涡旋盘端板背面、十字滑环的下环面与机架固定端盖上表面相接触，十字滑环的环面为目标面，动涡旋盘端板背面和机架固定端盖上表面为接触面。以上接触对的接触类型均为摩擦接触，设置摩擦系数为0.04。在ANSYS Workbench提供的接触算法中选择Augmented Lagrange算法。插入接触工具检测出接触对的间隙和穿透都满足模拟计算的要求。

2.4边界条件及载荷设置

静态模型的边界条件：动涡旋盘与十字滑环接触模型中，动涡旋盘端板周边与静涡旋盘外圆接触，设置端板周围z方向的自由度为零；动涡旋盘公转平动，设置动涡旋盘轴套内壁面x、y方向自由度为零；动涡旋盘轴套顶部z方向自由度为零；十字滑环与机架相接触的凸键在滑槽内自由滑动，设置它在y、z方向上的自由度为零。十字滑环与机架接触模型中，对机架周边设置固定约束。在十字滑环与机架相接触的凸键上设置向右滑动0.055mm。在十字滑环同一侧的两个凸键上施加方向相反的垂直载荷，即将静态时十字滑环受到的正向压力F1、F2、F3、F4分别施加到相应的凸键上。

动态模型的边界条件：动涡旋盘与十字滑环接触模型中，用两个载荷步施加载荷，第1个载荷步中，设置端板周围z方向的自由度为零，动涡旋盘轴套内壁面x、y、z方向自由度为零。因为轴的转速为3 000r/min，十字环一个凸键受力最大时的速度为1m/s，所以在第2个载荷步中，令十字滑环外向右滑动0.055mm，即在十字滑环外圈所有节点上施加y方向位移0.055mm。在十字滑环同一侧的两个凸键上施加方向相反的垂直载荷，即将动态时十字滑环受到的正向压力F1、F2分别施加到相应的凸键上。

2.5结果与分析

十字滑环与动涡旋盘、十字滑环与机架静态磨损过程中的接触状态分析结果如图5、6所示，十字滑环与动涡旋盘动态磨损过程中的接触状态分析结果如图7所示。从图5～7中可以看出静态接触状态与动态接触状态是不一样的，虽然都存在滑动区域，但动态接触时十字滑环的滑动区域扩大到整个环面，并随着滑动进行不断向环边缘处集中。

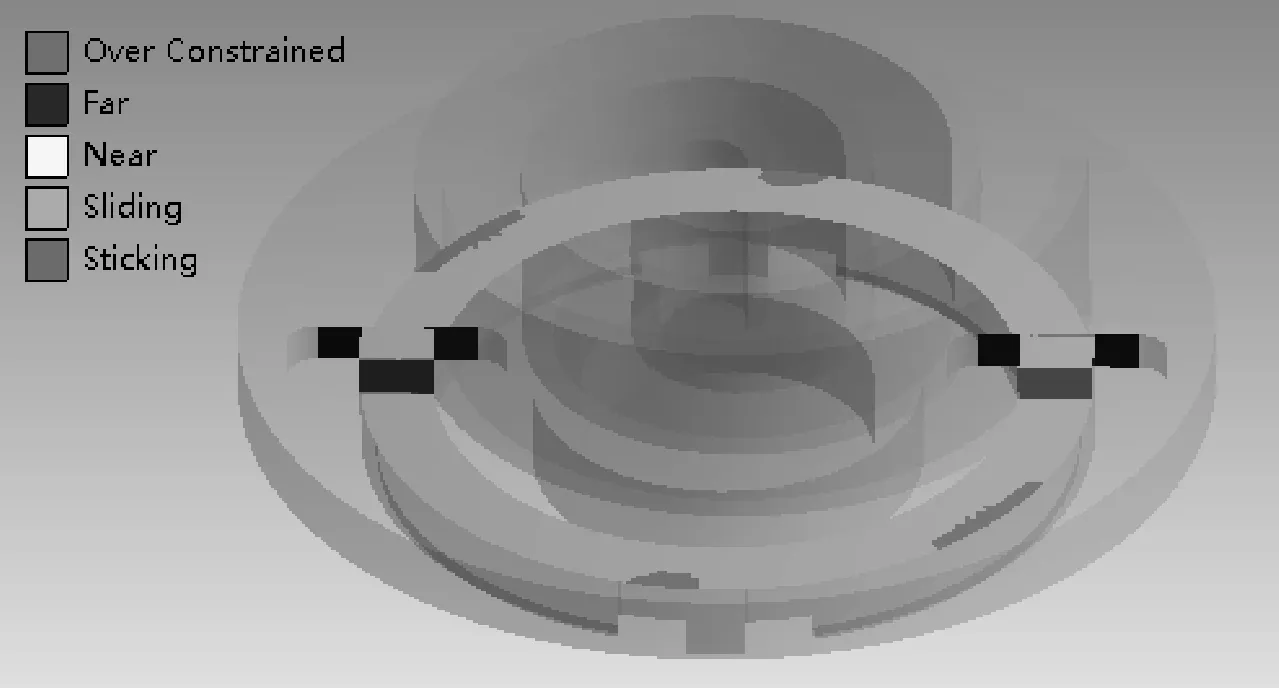
图5 十字滑环与动涡旋盘静态接触状态

图6 十字滑环与机架静态接触状态

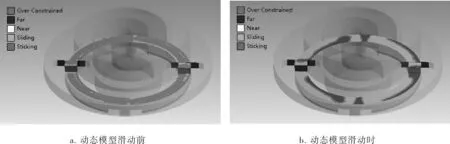
图7 十字滑环与动涡旋盘动态接触状态

图8、9分别表示了十字滑环与动涡旋盘静态接触时和动态接触时的受力情况。动涡旋盘与十字滑环接触时，十字滑环每个凸键的一个侧面受到来自动涡旋盘的正压力，从图8、9中都可以看出十字滑环凸键侧面的接触压力和摩擦应力都是边缘大，中间小，最大压力位于十字环凸键侧面的边界处。比较图8b、9b可见，十字滑环凸键的摩擦应力最大处均出现在凸键的键端处，也就是说该处也是十字滑环最容易磨损的地方。十字滑环的环面处受到的摩擦应力为0.3～2.0kPa，相比凸键处摩擦应力是较小的，在研究十字滑环摩擦磨损问题时可以将重点主要放在十字环凸键处。同时可以看出十字滑环在静态时受到的最大摩擦应力为3.1kPa，滑动速度最大时受到的最大摩擦应力为21.0kPa，但是由于十字滑环在压缩机内运行的速度是很快的，同时十字滑环凸键处长时间地受交变应力影响，因此因摩擦而引起的十字滑环凸键处的磨损是不容忽视的。

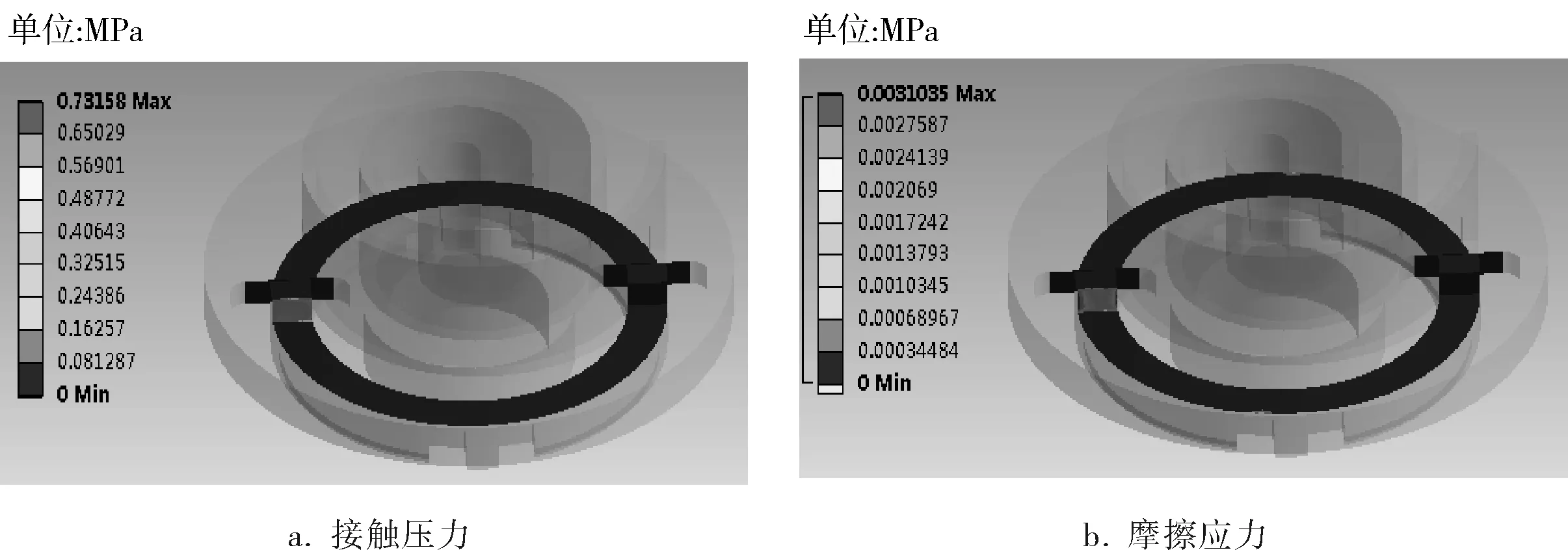
图8 十字环与动涡旋盘静态接触应力分析结果

图9 十字环与动涡旋盘动态接触应力分析结果

十字滑环与机架接触时静态磨损过程中的应力分析结果如图10所示。从图10中可以看出十字滑环与机架接触时主要受到的接触压力和摩擦应力都集中在十字滑环环面与机架固定端盖处，这是十字滑环与机架接触时最容易磨损的地方。与十字滑环与动涡旋盘接触一侧相比，十字滑环的凸键与机架滑槽处的受力、十字滑环环面的受力都比较小，并不是十字滑环摩擦磨损的最主要部位。

图10 十字环与机架动态接触应力分析结果

十字滑环的凸键键端处是遭受冲击最直接的部位，通过有限元软件分析得出十字滑环摩擦应力最大处也集中在十字滑环与动涡旋盘接触的凸键键端处。因此，十字滑环与动涡旋盘接触的凸键键端处的磨损应该最为严重，这与十字滑环实际磨损情况也是相符的。

3 十字滑环的摩擦损失

涡旋压缩机在运行过程中，十字滑环在动涡旋盘与机架之间不断地平移滑动，十字滑环与动涡旋盘和机架啮合面之间形成了两对摩擦副，该摩擦属于滑动摩擦，十字滑环与滑槽之间的滑动摩擦系数与摩擦副的材料、表面加工精度、装配精度有关[11]。摩擦力表示为f1、f2、f3、f4，一般十字滑环与动涡旋盘和机架之间的摩擦系数μ1、μ2取值为0.01～0.06。于是十字滑环与动涡旋盘和机架之间的摩擦损失功率Pf表示为：

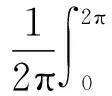
(5)

图11给出了不同主轴转速n下的十字滑环的摩擦功率。

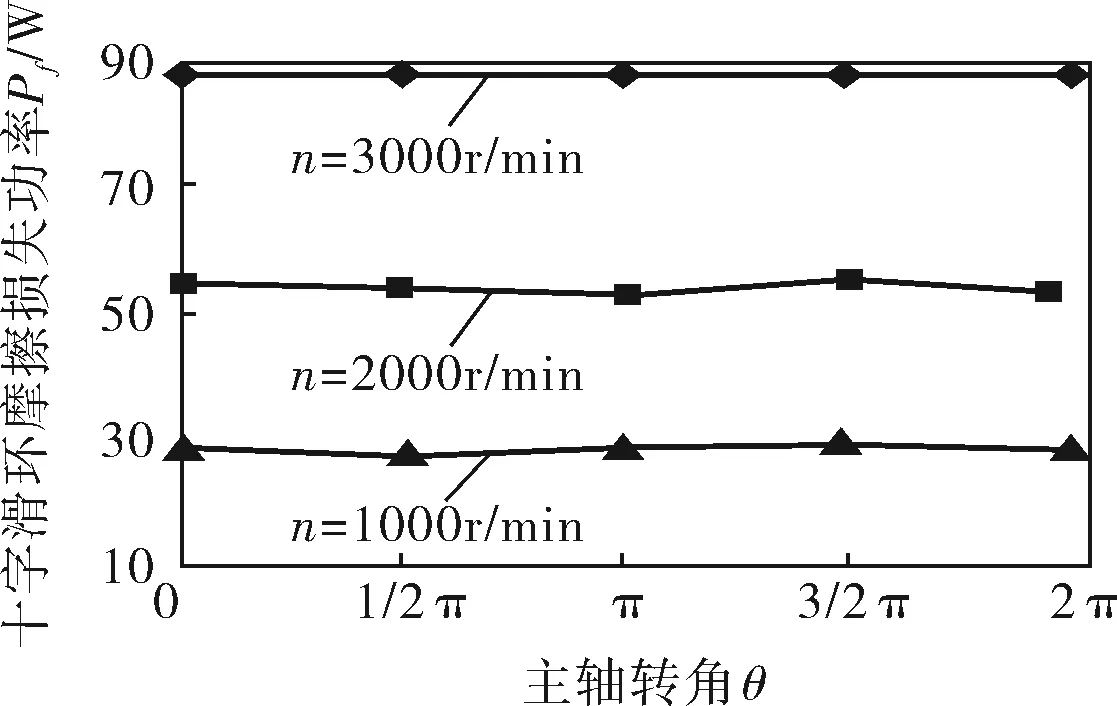
图11 不同主轴转速下的十字滑环的摩擦功率

由图11中可以看出，十字滑环的摩擦损失功率随主轴转速的增大而增大，当主轴转速分别为1 000、2 000、3 000r/min时，十字滑环的摩擦功率在20～90W之间，且计算可得，十字滑环的摩擦损失功率约占整机摩擦损失功率的10%。与该样机整体将近1kW的摩擦功率相比，这一部分的摩擦功率相对较小。十字滑环长时间运行带来的损失可分为两部分，即因摩擦引起的能量损失和因磨损引起的材料损失。通过分析可以得出十字滑环的摩擦损失功率是很小的，故因十字滑环的磨损而引起的材料损失，造成动、静涡旋盘不能精确啮合的现象就成为了研究十字滑环摩擦磨损的重点。

4 结论

4.1作用在十字滑环上的正压力的大小主要受自转力矩Mr和十字滑环沿支架滑槽产生的往复惯性力Fm的影响。

4.2十字滑环在动涡旋盘滑槽处受到的摩擦力随主轴转角按类似正、余弦函数规律变化，十字滑环在机架滑槽处受到的摩擦力大小在一个运动周期内基本不变。十字滑环与动涡旋盘滑槽接触的凸键在运行过程中将不断受到冲击，这是造成十字滑环磨损的主要原因。

4.3十字滑环与动涡旋盘的接触部位是十字滑环摩擦磨损最严重的部位，其中摩擦应力最大处出现在十字滑环凸键的键端处，该处是十字滑环最容易磨损的地方。

4.4十字滑环摩擦损失功率为20～90W，约占整机摩擦损失功率的10%。

[1] 李连生.涡旋压缩机[M].北京：机械工业出版社，1998：27～125.

[2] 周家胜.涡旋流体机械防自转机构[J].压缩机技术，1995，(3)：5～10.

[3] 李超，孙照岚，赵嫚.无油润滑涡旋压缩机动静涡旋端面摩擦测试装置[J].化工机械，2014，41(2)：180～183.

[4] 曹霞，陈芝久，刘振全.立式高压型涡旋压缩机摩擦副分析[J].上海交通大学学报，2000，34(9)：1228～1232.

[5] 刘兴旺，刘振全，李超，等.涡旋压缩机摩擦损耗和泄漏损耗研究[J].压缩机技术，2006，(3)：1～4.

[6] 王国梁，高秀峰，冯诗愚，等.涡旋压缩机防自转机构载荷改善分析[J].流体机械，2000，28(8)：39～41.

[7] 胡旭，屈宗长，于漠南，等.平动回转式压缩机的几何理论[J].中国机械工程，2011，22(16)：1896～1900.

[8] 李超，郑尚书，赵嫚，等.涡旋压缩机小曲拐防自传机构动力特性分析[J].中国机械工程，2014，25(2)：236～241.

[9] 温诗铸，黄平.摩擦学原理[M].北京：清华大学出版社，2002.

[10] 余洋.涡旋压缩机动力特性及仿真模拟研究[D].兰州：兰州理工大学，2014.

[11] 刘佐民.摩擦学理论与设计[M].武汉：武汉理工大学出版社，2009.

StudyonFrictionandWearofSlip-ringAnti-rotationMechanisminScrollCompressor

LIU Xing-wang1,2, WANG Yang1

(1.SchoolofPetroleumandChemicalEngineering,LanzhouUniversityofTechnology,Lanzhou730050,China;2.WenzhouInstituteofPumpandValve,LanzhouUniversityofTechnology,Wenzhou325000,China)

The cross slip ring’s friction and wear has a great influence on both scroll plate’s precise meshing and scroll compressor’s efficient operation. In order to explore wear and friction loss of the cross slip ring, having force-balance equation for the orbiting scroll and cross slip ring based to work out a calculation method for positive pressure at the cross slip ring’s convex key was implemented, including having prototype data based to get friction’s periodic variation of the cross slip ring. Through making use of the finite element software to analyze friction contact of the cross slip ring in reciprocating motion, and its real time contact status and the friction force distribution, the cross slip ring’s friction loss power was obtained. The results show that, at the orbiting scroll, the friction force of the cross slip ring changes with the principle axis which varies like the sine and the cosine function, and the end of cross slip ring’s convex key is impacted continuously, this mainly incurs the wear of the cross slip ring; and at the rack’s sliding chute, the friction force of cross slip ring keeps steady in a period of motion; and the end of convex key of cross slip ring area that contacting with orbiting scroll is easy to be worn; the cross slip ring’s frictional loss stays at 20 to 90W which accounting for about 10% of the total friction loss.

scroll compressor, slip-ring anti-rotation mechanism, friction, wear

*国家自然科学基金项目(51265026)，浙江省自然科学基金项目(Y1080079)。

**刘兴旺，男，1970年11月生，副教授。甘肃省兰州市，730050。

TQ051.21

A

0254-6094(2016)06-0803-07

2016-01-05，

2016-09-30)

(Continued from Page 769)

ultrasonic wave influence, this demonstrates a much better synergy between the temperature field and the velocity field.

Keywordsheat exchanger, numerical simulation, ultrasonic cavitation, Nusselt number, field synergy theory, field synergy number