长期生存率比较的统计检验法*

陈金宝 邱李斌 王北琪 曾 洁 陈慧林 侯雅文 陈 征△

长期生存率比较的统计检验法*

陈金宝1邱李斌1王北琪1曾 洁1陈慧林1侯雅文2陈 征1△

目的针对基于生存数据的长期疗效分析的问题，特别是两条生存曲线出现交叉或危险率不成比例的情况下，比较在特定时刻点后组间生存率的差异，本文主要介绍组合检验法ZOLS、ZSP，p和χ2三种检验的适用情况。方法在两组危险率不满足比例风险假定的前提下，对生存曲线交叉和后期差异大的两个例子，分别使用ZOLS、ZSP，p和χ2三种方法检验在不同时刻点之后组间生存率的差异。结果两个例子中，ZOLS检验与χ2检验对不同时刻点之后的组间生存率差异进行检验，均能得出较为一致的结论，并且与实际情况符合。而ZSP，p检验的结果与前两种相比有差异。结论结合实例分析，在比较长期疗效或者生存曲线特定时间点后的生存率时，建议使用ZOLS检验与χ2检验。

生存分析 组间生存率比较 非参数检验 长期疗效分析

在医学临床研究中，组间生存率差异的检验是常见的研究问题之一，经典方法如统计软件SPSS 22.0采用的log-rank、Breslow和Tarone-Ware检验，均是对组间生存曲线进行整体检验，当两组危险率不满足比例风险假定时，这三种检验［1－4］均不适用。例如在一项评估两种治疗方法对肾透析患者疗效的临床研究中［1］，两条生存曲线存在交叉（图1），并经 Grambsch-Therneau检验［2］得到两组危险率不满足比例风险假定（χ2＝8.70，P＝0.003），因而 log-rank检验结果（χ2＝2.53，P＝0.112）不可靠，外科放置组与皮下放置组的平均感染时间分别为18.527月和23.649月，结合图1发现10个月之后两组间生存率可能有较大的差异。此时可以使用避免交叉点前后差异相互抵消的two-stage检验［3－4］，从而得到整体上两组间生存率有统计学差异（P＝0.025）。但依旧很难给出哪种治疗法生存率更高的结论，因为交叉点前、后的生存率高低是相反的。陈金宝等［5］建议使用固定点处组间生存率的比较法，但很多时候更关注的是哪种治疗法在长期阶段有着更高的生存率，如在实际的临床研究中，研究者往往对特定时间点后的部分（或阶段）生存率的差异更感兴趣，在上述肾透析研究（图1）中关注第5个月之后或第15个月之后两组之间生存率是否有差异等。本文将介绍两生存曲线在长期阶段（特定时间点后）生存率比较的三种检验方法［6］，Nelson-Aalen估计线性组合的ZOLS检验，Kaplan-Meier估计线性组合的ZSP，p检验以及二次型形式的χ2检验，并应用于两个实例来分析说明。

图1 肾透析患者分别进行外科放置导管和皮下放置导管的生存曲线

模型简介

本文只考虑两条生存曲线长期（特定时间点后）生存率的比较。假设第k组有样本量nk，其中k＝0，1，tj表示第j个个体的事件发生时间，且t1≤t2≤……≤tm，dkj表示第k组在时间tj发生的事件数，Ykj表示第k组在时间tj的风险人数。Kaplan-Meier估计生存率率及其方差估计值分别是

比较长期（特定时间点后）生存率的差异，原假设H0∶｛S1（t0）＝S0（t0）｝∩｛λ1（t）＝λ0（t），t＞t0｝，其中λk（t）表示第 k组（k＝0，1）在时间点 t的危险率。原假设包括 H01∶S1（t0）＝S0（t0）和 H02∶λ1（t）＝λ0（t），t＞t0两个子假设，其中H01表示在t0时刻生存率相等，而H02表示时间点t0后的危险率无差异；备择假设H1:两个子假设中至少有一个子假设不成立。

针对于特定时刻后生存率比较，本文介绍组合检验法中三种检验统计量［6］:

1.组合检验的基本统计量

（1）子假设H01的检验统计量为 ZNA（t0）:利用 Nelson-Aalen法估计累计危险率，设

（2）子假设 H02的检验统计量 ZLR（t0），基于 logrank检验法。从时刻点 t0开始可设得 XLR（t0）＝差一致性估计值为dj）/（Yj－1）｝dj，其中的 dj和 Yj分别是已发生事件总人数和正处于风险总人数，则检验统计量为:

并且检验统计量ZLR（t0）服从标准正态分布。

2.组合检验法

为了检验组合原假设H0，利用上述检验统计量ZNA（t0）和 ZLR（t0），本文主要阐述组合检验的两种检验法，包含三个检验统计量，方法如下:

（1）线性组合检验

①ZOLS检验统计量

假设在H0成立的条件下，基于Nelson-Aalen估计法，对 ZNA（t0）和 ZLR（t0）两个检验统计量进行线性组合，则检验统计量为:

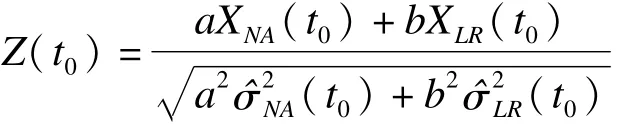
其中，可以根据实际情况合理调整权重a和b大小，Logan等［6］通过模拟实验发现，当对权重a和b分别赋值a

不错，并且此时统计量Z（t0）化简后表达式为:

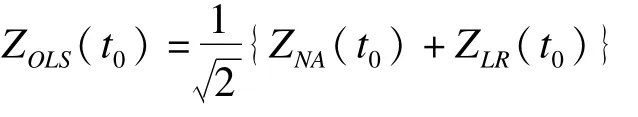
检验统计量ZOLS类似于检验多终点事件的普通最小二乘法（ordinary least squares，OLS），并且服从标准正态分布。

②ZSP，p检验统计量

对于子假设H01的检验，基于Kaplan-Meier估计法来计算t0时刻不同组别的生存率的差值及组合样本的生存率和方差，在估计生存率差值的方差时用到组合样本。类似于部分分组log-rank检验法，构造一种特殊的线性组合检验（SP，p）统计量:

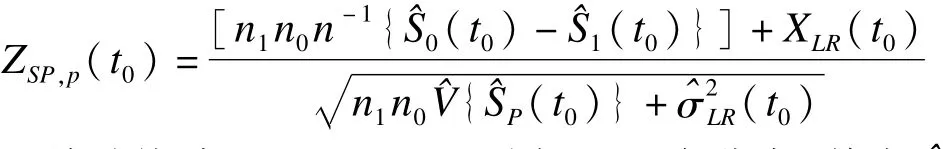
并且检验统计量ZSP，P（t0）服从标准正态分布，其中＾Sp（t0）表示在t0时刻组合样本n0＋n1的生存率估计值。

（2）二次型 χ2检验法

通过对组合检验基本统计量ZNA和ZLR的构造分析，可得（ZNA（t0），ZLR（t0））服从均值为（0，0），方差和协方差矩阵可由估计得到的二元正态分布，二次型检验法对二元正态分布整体进行假设检验，这时检验统计量逼近卡方分布，构造得到检验统计量为:

在原假设H0成立的前提下，检验统计量χ2（t0）服从自由度为1的卡方分布。

实例应用

本文给出两个例子来说明上述方法的应用，一个两条生存曲线交叉，另一个是生存率后期差异大。

1.两条生存曲线交叉

在一项评肾透析患者疗效的研究中［1］，共有119名患者，其中43人进行外科放置导管，76人进行皮下放置导管（删失率分别为65.1%和85.5%）。终点事件为肾功能不全患者初次发生通道口感染，右删失为导尿管失效和试验结束时终点事件尚未发生，图1显示两条生存曲线大概在第8个月左右相交，不满足比例风险假定。由表1可见，ZOLS检验结果显示在第10、15和20个月后，两组间生存率差异均有统计学意义，结合图1发现对应时间段皮下放置导管的生存率均较外科放置导管的高，而在第5个月后两组间生存率差异没有统计学意义。ZSP，p检验结果与ZOLS检验结果完全相反。χ2检验结果显示在第5、10、15和20个月后，两组间生存率差异均有统计学意义。Logan等［6］通过模拟研究发现，ZOLS检验与χ2检验不论I类错误还是检验效能都有较好且一致的表现，建议综合ZOLS检验和χ2检验结果来得出结论。

表1 不同检验方法在例1上的应用结果

2.生存率后期差异大

一项关于万络预防腺性息肉瘤的研究［7］共收集了262例曾患结肠直肠的患者，其中132例服用昔布类药物:万络，130例服用安慰剂，中位生存时间分别为9.71个月和10.04个月，右删失率为22.0%和37.7%，由于原文数据无法获得，因此参照Royston和Mahesh［8］的方法模拟产生了本例的数据。终点事件是发生心血管事件（心脏病中风），到研究截止时间尚未发生终点事件为右删失，图2显示服用万络患者比服用安慰剂的患者在18个月后出现心血管事件的几率相对增加，但在18个月之前两组患者出现心血管事故的生存率基本一致。由表2可见，log-rank检验结果显示两组间整体无统计学差异，而且Grambsch-Therneau检验［2］显示两组不满足风险比例假设（χ2＝4.45，P＝0.035），two-stage检验结果显示两组整体上有统计学差异。长期检验的ZOLS检验显示在第6和12个月后两条生存曲线生存率均无统计学差异，而在第18和24个月后差异均有统计学意义。ZSP，p检验显示在四个时间点后的生存率差异均无统计学意义。χ2检验显示在第6个月后的生存率差异无统计学意义，而在第12、18和20个月后生存率差异有统计学意义。结合图2和 Logan等［6］的模拟研究，ZSP，p检验结果可能与实际不符，ZOLS检验与χ2检验能给出较为合理的结果，即患者在使用万络一段时间之后能够增加心血管事件发生的概率。

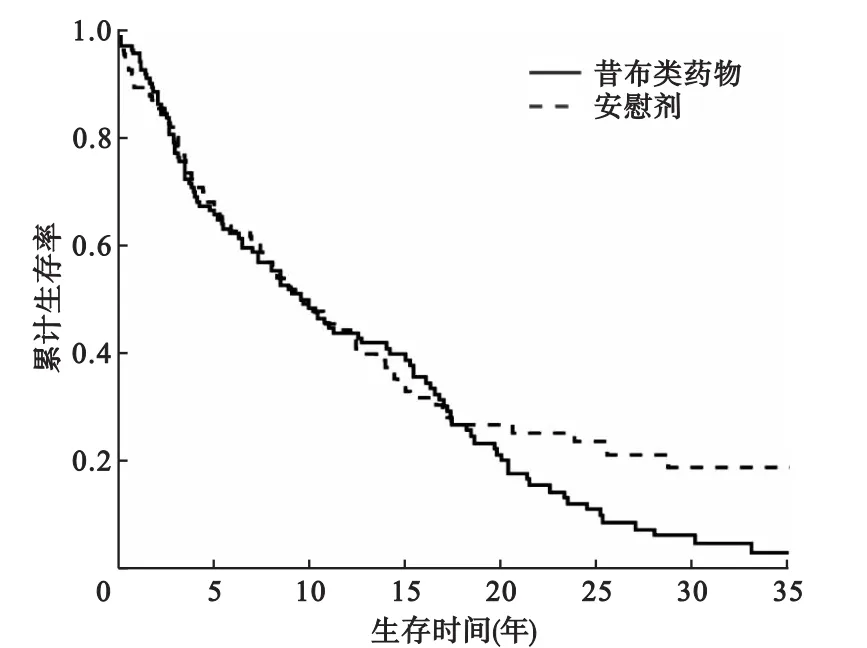
图2 结肠直肠腺瘤患者分别服用昔布类药物和安慰剂的生存曲线

表2 不同检验方法在例2上的应用结果

讨 论

两条生存曲线比较是医学临床研究中重要的统计分析方法。当两组危险率满足比例风险假定，可采用常规的log-rank检验或Breslow检验等方法，但当两组危险率不满足比例风险假定，采用two-stage检验可以克服常规方法的不足。以上都是检验组间整体的生存率差异，然而在实际临床研究中，特别是不满足比例风险时，整体检验法还是无法确定生存率谁高谁低，这时可以采用某固定时刻点组间生存率的比较检验法［5］，但这种检验法只关注某固定时刻点上生存率的差异，还是不能做整段的生存率比较，这时若是对长期效果感兴趣则可以采用本文介绍的某特定时刻后生存率长期比较检验法，其可以关注某特定时刻后组间生存率的差异。Logan等［6］对长期检验的三种检验统计量，在不同删失率下进行模拟研究，发现ZOLS检验在不同删失率下均表现出较高的稳健性和适用性；χ2检验在删失率较低（20%以下）的情况下对组间差异更加敏感；ZSP，p检验法不论删失率的高低，均易得出与实际情况不相符合的结果。结合本文两个例子分析结果，笔者建议在分析之前先绘制生存曲线图和进行成比例假设检验，也建议采用线性组合检验法的ZOLS检验，它相对ZSP，p检验和χ2检验具有较好的适用性和稳健性。

［1］Klein JP，Moeschberger ML.Survival Analysis:Techniques for Censored and Truncated Data.Second Edition.New York:Springer，2003.

［2］Grambsch P，Therneau T.Proportional hazards tests and diagnostics based on weighted residuals.Biometrics，1994，81（3）:515-526.

［3］Li H，Han D，Hou Y，et al.Statistical Inference Methods for Two Crossing Survival Curves:A Comparison of Methods.PLoS ONE，2015，10（1）:e0116774.

［4］李慧敏，韩栋，陈征，等.生存曲线交叉时统计推断的比较和选择.中国卫生统计，2013，30（5）:668-672.

［5］陈金宝，邱李斌，王北琪，等.固定点处组间生存率比较的统计检验法.中华流行病学杂志，2015，36（2）:186-188.

［6］Logan BR，Klein JP，Zhang M.Comparing Treatments in the Presence of Crossing Survival Curves:An Application to Bone Marrow Transplantation.Biometrics，2008，64（3）:733-740.

［7］Bresalier RS，Sandler RS，Quan H，et al.Cardiovascular Events Associated with Rofecoxib in a Colorectal Adenoma Chemoprevention Trial.N Engl JMed，2005，352（11）:1092-1102.

［8］Royston P，Mahesh KBP.The use of restricted mean survival time to estimate the treatment effect in random ized clinical trials when the proportional hazards assumption is in doubt.Statistics in Medicine，2011，30（19）:2409-2421.

国家自然科学基金（81202288）、广州市科技计划（2012J5100023）、广东省大学生创业创新训练计划（1212113039）、南方医科大学科研启蒙计划（B1012444）

1.南方医科大学公共卫生学院（广东省热带病研究重点实验室）生物统计学系（510515）

2.暨南大学经济学院统计学系

△通信作者:陈征，E-mail:zchen@smu.edu.cn

（责任编辑:郭海强）