落差指数法在湘乡水文站的应用初探

刘雪桂（湘潭水文水资源勘测局 湘潭市 411100）

落差指数法在湘乡水文站的应用初探

刘雪桂
（湘潭水文水资源勘测局 湘潭市 411100）

用落差指数法进行单值化处理，可获得水位流量之间确定的函数关系，提高水文站在受洪水涨落和变动回水顶托影响时段推流精度，为水文预报和资料整编提供可靠方法。利用Matlabl软件的强大计算优势，根据湘乡站的测站特性，选择合适的线形，编制相应的程序。利用湘乡站实测的资料，获得该段时期内的对应参数。落差指数法不仅可以提高推流精度，而且求解方便，计算快捷，极大减轻测站人员的劳动强度，节省人力、物力、财力，因而具有较强的实用价值。

落差指数法 数学模型 Matlab 最优拟合

1 落差指数法的基本原理

天然河道的洪水波运动规律可以用圣维南方程组描述，它由连续方程式（1）和动力（运动）方程式（2）组成：

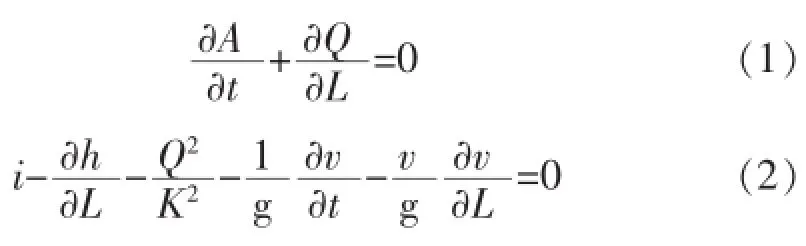
式中 Q——流量（m3/s）；

K——流量模数；

i——稳定流比降；

L——流程；

h——水深；

A——过水面积；

v——流速；

t——时间；

g——重力加速度。

如把动力（运动）方程式（2）加以变形，即为水位流量关系严谨的数学表达式：

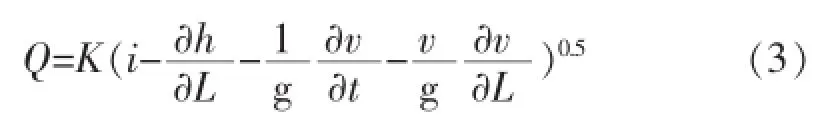
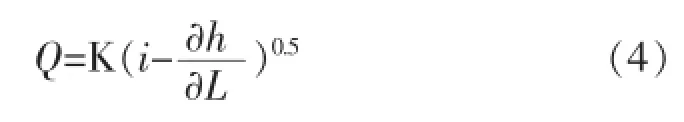
在稳定的天然河槽中，流量模数K和稳定流水面比降与水深基本上成单值关系。附加比降取决于洪水涨落和回水顶托的综合影响。表示的实际上就是扩散波时水面的实际比降，对于两固定断面来说，其值可表示为：

式（5）中△z表示两固定断面的水位差。由式（5）代入式（4），得：

式（7）中q称为单值化流量（实质为落差指数法校正因素）。

式（7）中落差指数0.5是理论值，它是水流阻力平方律的反映。在实际应用中，由于各种因素的影响，水面线不是直线而是曲线，尤其是两固定断面较远时，水面线比较明显地表现为曲线，式（7）的处理不一定都能达到满意的效果。因此在实际工作中经验性地将式（7）表示为：

式（8）即为落差指数法的基本公式，式中β为综合落差指数。

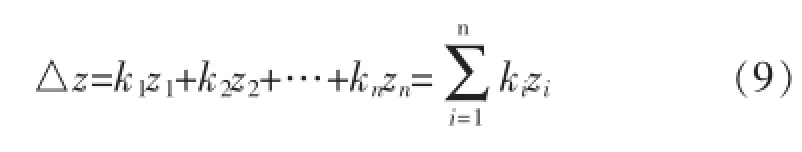
式（9）中ki（i=1，2，…n）为综合落差权重系数，且k1+k2+…+kn=1。

2 水位关系模型的确定及Matlab编程实现

2.1 水位关系模型的确定

由式（6）可知，单值化流量q与水位z成单值关系，可以表示为：

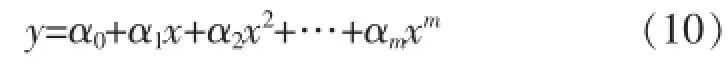
式（10）即水位流量拟合模型，式中y=q；x=z；a0，a1，a2，…，am为待定系数。

以n次实测流量的相应数据代入式 （9）、（10），考虑模型误差和观测误差，加入残差ε即得n个方程组。写成矩阵：

最优拟合模型的评判标准是水位流量测点标准差，采用式（10）拟合时为：

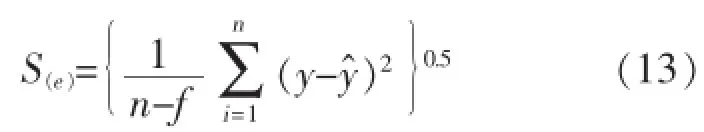
式（13）中n-f为自由度，f=m+1，其中f为待定未知数个数，m为拟合次数。

2.2 Matlab编程实现

要使模型拟合的效果最佳，即S（e）取得最小值。从上推导可知，S（e）不仅与拟合次数m，还有落差指数β及落差权重系数k有关，可以表示为：

其中拟合次数m，可以设定，一般取二阶或三阶即可取得较好的拟合效果；落差指数β的优选，对于单一落差(只有两固定断面)来说，李正最[6]等曾提出直接解算的方法，倒不失为一种有效的途径，而对于综合落差来说，直接解算方法就显得力不从心了。本人在研究落差指数β和综合落差权重系数k的优化先后问题时发现，式（9）属于一次函数方程，而式（8）属于指数函数方程，根据两种函数的性质不同，应该先作落差指数β的优选，而不考虑落差权重系数k，然后在此基础上作落差权重系数k的优选，即两参数同时达到最优，最佳的落差指数β应在一次优化的附近，这样就不必一一试算了。

Matlab是一种功能强大的数学软件，广泛的内置函数可大大简化编程的过程。基于试算法的基本思想，编写了计算落差指数法的Matlab程序，其主要是通过内置函数polyfit实现单值化流量与水位的多项式拟合，通过corrcoef函数计算相关系数，从而比较优选出最佳方案。计算出单一落差指数β后，程序略作修改，就可计算综合落差权重系数k的优选。

3 落差指数法在湘乡水文站的应用初探

3.1 湘乡站的基本情况

湖南省湘乡水文站，设立于1958年1月，位于湘乡市学前街65号，即：东经112°31′，北纬27°43′；流域控制集水面积6 053 km2，干流全长232 km，干流平均坡降0.69‰，至河口距离53 km。湘乡水文站是国家基本站，属国家重要水文站，湘江一级支流涟水控制站。

测验河段顺直、平整，河床由细沙、卵石组成，两水边系岩石，附近部分有局部冲淤影响，断面形状为“U”型，无分流、串沟、漫滩现象，断面右岸水边部分生有水草，下游控制断面急滩进口处较严重，下段局部为乱石堆积。

断面上游：61 km有水府庙电站，常年发电并兼顾灌溉，汛期暴雨闸门开关频繁、引起湘潭水文站水位急剧变化。43 km处有韶山灌区洋潭拦河坝，坝上右侧有一引水渠——韶山灌区总干渠，供下游工农业及生活用水。

断面下游：350 m处有一空腹式公路桥东山大桥。1 800 m处碧洲公园左侧有2 m高的拦水坝，后在坝上修了一平坦式桥，通往公园内。右侧有一急滩，两岸护坡。2011年公园四周修挡板墙，高约2.5 m。2008年老城至新城跨越涟水通过公园修建一座市内连接桥。断面左侧至2011年已修防洪大堤约3.0 km，右侧约1.5 km。8 km处有东山电站常年拦水发电。

高水上游水府庙电站开闸泄洪，洪水波传播速度快，比降大，用连时序法推流。中低水受上游洋潭滚水坝控制，流速较稳定，低枯水受下游急滩控制，有时段性变迁，均用临时线推流，测验河段属不经常性冲淤，但有局限性，下游急滩进口处夏季易生水草，且该段多为乱石堆积，易受漂浮物阻塞，引起水位流量关系曲线变迁。

2015年7月下旬，下游东山电站改建完成，关闸蓄水试运行，站水位较平常抬高达1.0 m，同水位流量相差达2.7倍，水位流量关系紊乱，采用连实测流量过程线法推流。

根据影响湘乡水文站水位流量关系的主要因素：①洪水涨落率影响；②下游变动回水顶托影响；③测验河段局部冲淤影响；④水草影响等，拟改进流量测验方案采用落差指数法推流。

3.2 落差指数法单值化处理方法

3.2.1 落差指数法单值化处理运用的外部条件

落差指数法应用的关键技术是观测落差水尺断面的选定。根据现有规范规定的定线误差指标和现有测量测验设备的测验精度，可以从落差指数法的流量计算公式估算落差水尺的最小落差范围。

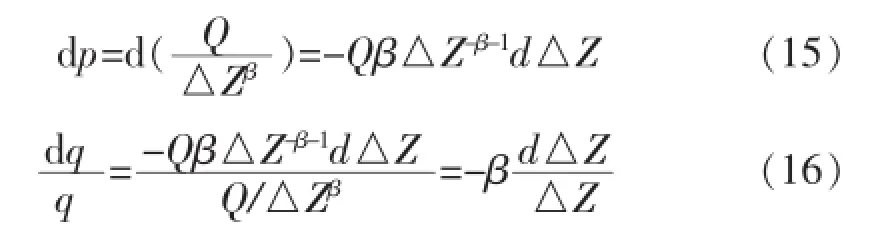
假设观测落差水位误差d△Z为±0.02 m （包括观测水位和校测水尺的误差在内），校正流量误差落差指数β值一般接近0.5，取用0.5。则需要的最小落差△Z为：

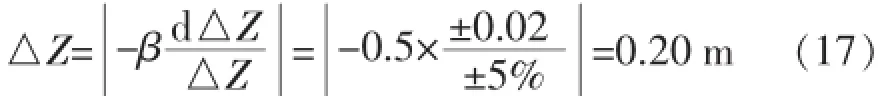
因此“综合落差不小于0.20 m”成为布设落差水尺断面的基本条件。

3.2.2 落差水尺断面的布设

由于事前并不知晓满足最小落差范围为0.2 m的断面在哪，且不同的洪水组合和不同的水位级其落差也不一定相同，故落差指数法实际应用时需根据河道比降和实地测量进行估算，且估算的落差水尺断面并不一定就是实际的最好落差水尺断面，因此，落差水尺断面选定前，需在估算的落差水尺断面附近布设几组断面进行比选。

根据“综合落差不小于0.20 m”的原则，在湘乡水文站测验断面上下游一定范围内，布设了3组水尺进行比选，见图1。

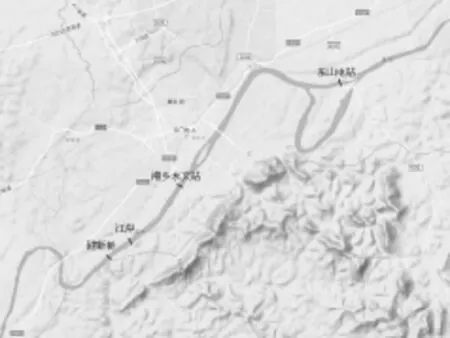
图1 水尺断面布置图

3.2.3 资料的收集与分析计算

对布设的三组水尺进行水准测量，在测流的同时，组织测站人员进行上下游同步观测水位，资料如表1。

对所取得的资料，按单一落差和综合落差两种方案运用所编的程序进行曲线拟合和各参数的优选，计算成果如表2。

表2中k1系下游落差权重系数，k2系上游落差权重系数。

从表2可以明显看出：综合落差方案优于单一落差方案，加入落差权重系数后的方案优于未加入落差权重系数的方案；综合落差指数法适宜湘乡水文站应用。

标准差稍微偏大的原因：实测流量次数过少；软件采用的是二次多项式拟合曲线，与天然河流的曲线有一定差别，因此还需要利用上述公式计算出校正流量后，人工定线，并进行曲线检验，以检验计算机优选的参数的合理性。

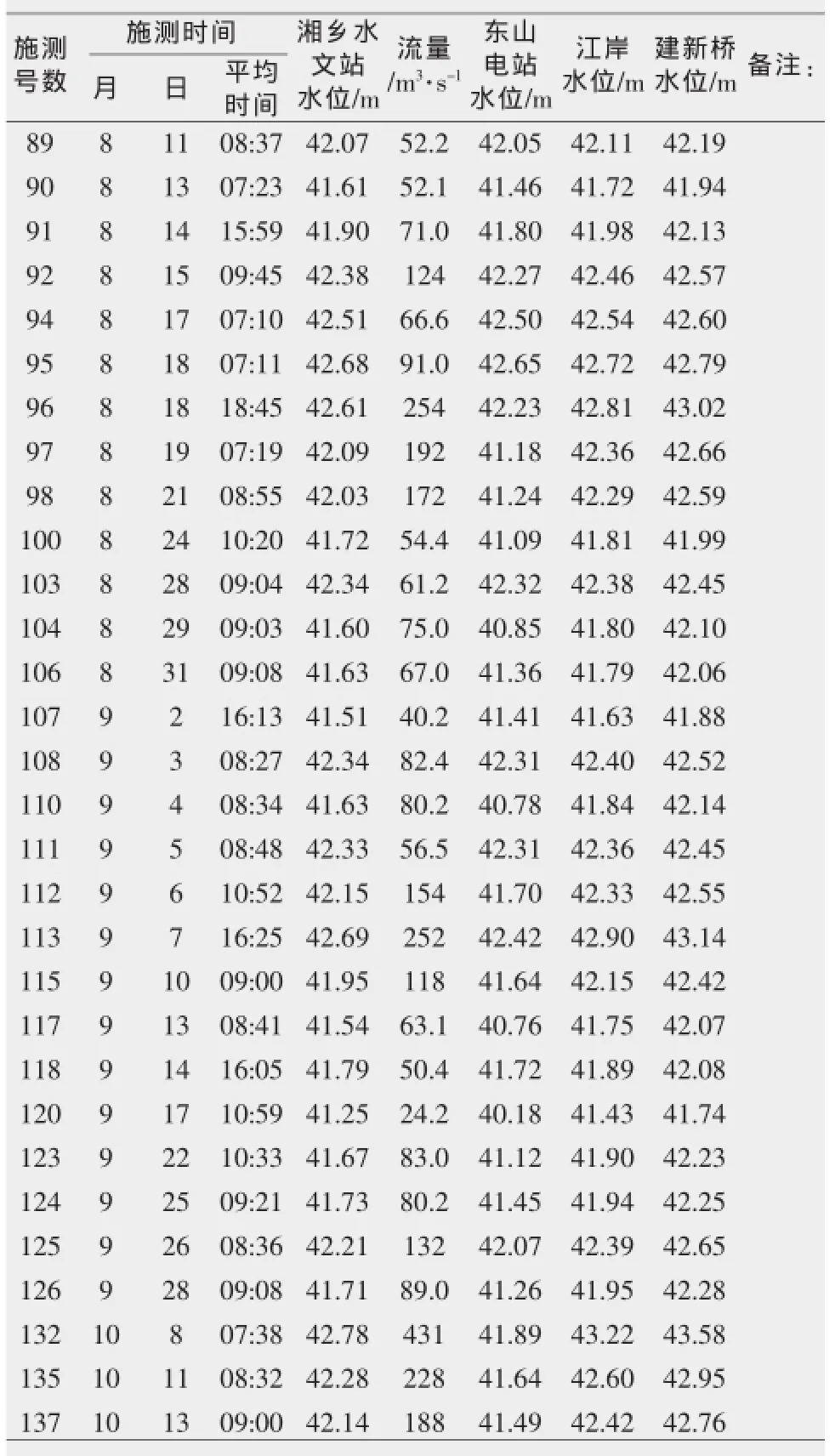
表1 湘乡水文站实测流量及上下游同时观测水位

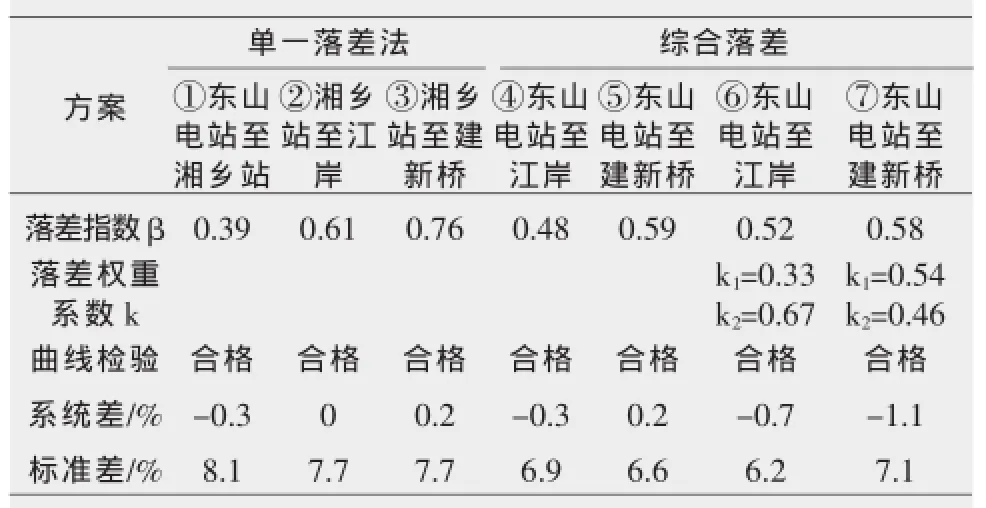
表2 落差指数法方案分析统计表

现列出方案⑥（表2）的曲线拟合方程：

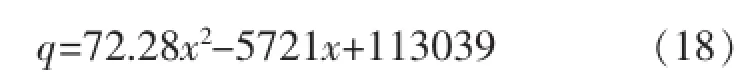
点绘方案⑥湘乡水文站水位～校正流量关系图，并通过点群中心定线（Q90、Q94、Q100误差超过3倍标准差，按特异值处理，舍弃），见图2。

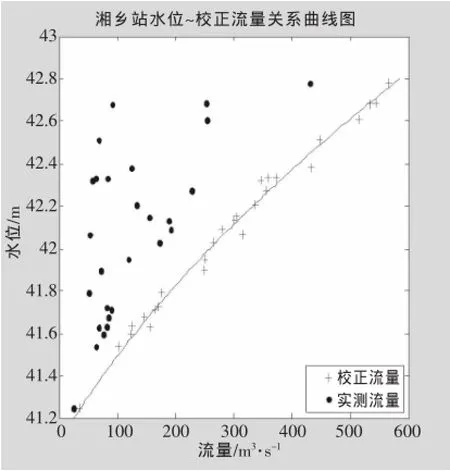
图2 湘乡站水位～校正流量关系曲线图

4 结 论

湘乡水文站适宜应用综合落差指数方案⑥（表2）。由于目前所取得的资料（30次）有限，无法对模型进行验证，对所取得的参数进行率定。用Matlab编程，简洁、方便。落差指数法不仅可以提高推流精度，而且求解方便，计算快捷，极大减轻测站人员的劳动强度，节省人力、物力、财力，因而具有较强的实用价值。对受水利工程影响的测站流量测验改革，落差指数法应用值得大力推广。

[1]芮孝芳.水文学原理[M].北京：中国水利水电出版社，2004.

[2]SL 247-2012.水文资料整编规范[S].中华人民共和国水利部.

[3]钱学伟，陆建华.水文测验误差分析与评定[M].北京：中国水利水电出版社，2007.

[4]张志涌，杨祖樱.MATLAB2012a教程[M].北京：北京航空航天大学出版社，2010.

[5]李正最.水位流量关系分析中落差指数直接解算方法及应用[J].中南水力发电，2002，（3）.

2016-04-29）

刘雪桂（1969-），男，湖南湘乡人，大学本科，工程师，主要从事水文测验，水文资料整编，水文分析计算与研究工作。