油页岩气体热载体干馏炉内温度分布的模拟及验证*

柏静儒 冯 妍 辛思谕 张 伟 王 擎 秦 宏

(东北电力大学 油页岩综合利用教育部工程中心)

油页岩气体热载体干馏炉内温度分布的模拟及验证*

柏静儒**冯 妍 辛思谕 张 伟 王 擎 秦 宏

(东北电力大学 油页岩综合利用教育部工程中心)

对直径400mm、高1 089mm、包括中心送风和边壁送风的气体热载体干馏炉采用CFD-Fluent方法进行仿真，模拟油页岩在炉内干馏过程中的温度场。由于物料堆积阻碍流动和传热，因此将区域设置为多孔介质模型，并通过对不同流动模型(层流模型与湍流模型)和不同边界条件(中心送风装置壁面恒热流与恒壁温)的对比，确定最佳设置。由最终模拟结果可以看出温度在纵向与横向具有递减性，流动模型不同，温度渗透不同；边界条件不同，反应进行与温度均匀性表达不同，同时与实验数据对比，发现层流模型下中心管恒热流边界条件与实验更相似相符。

干馏炉 油页岩 固定床 Fluent 多孔介质

油页岩作为石油的替代能源，就是将低能量密度的页岩转变成高品位能源。解决这一问题的核心是油页岩干馏，目前对油页岩干馏的研究都通过实验与模拟的方法进行。秦宏等对油页岩气体热载体干馏炉内温度分布和布气方式对温度的影响等进行了实验研究，得出干馏段温度高并且中心与边壁联合进气使温度分布较均匀等结论，却不能直观反映整体的温度分布与影响程度[1～3]。范贤振等借助Fluent软件模拟了200MW四角切向燃烧煤粉炉炉内的燃烧过程[4]，邓中乙等利用Fluent软件对加压喷动流化床煤气化进行了模拟[5]。Fluent软件作为目前功能全面、适用性广的CFD软件之一，不仅可以解决化学反应和流动方面的实际问题，还能直观、整体地反映炉内流动、温度、压力及生成物浓度等的分布。因此笔者基于Fluent软件，建立油页岩热解的热解动力学模型，探讨在不同流动模型和边界条件下与实验结果最相符的设置，为优化油页岩热解提供模拟基础。

1 几何模型

笔者研究的是基于实际的实验炉体[1]，炉体结构如图1所示，炉体由上至下依次分为干燥段、干馏段、冷却段和出焦段。炉内进气分为边壁进气和中心进气(图2)，其中，中心管上有4根布气管，呈十字形，每根布气管上在两侧斜向下45°位置交错布置5个直径5mm的圆孔；在中心管四臂横截平面上炉体外围设有一层边壁进气，在炉体内壁沿圆周分为4个象限，每部分在45°角上布置3个直径5mm的圆孔，相邻孔夹角为16°。

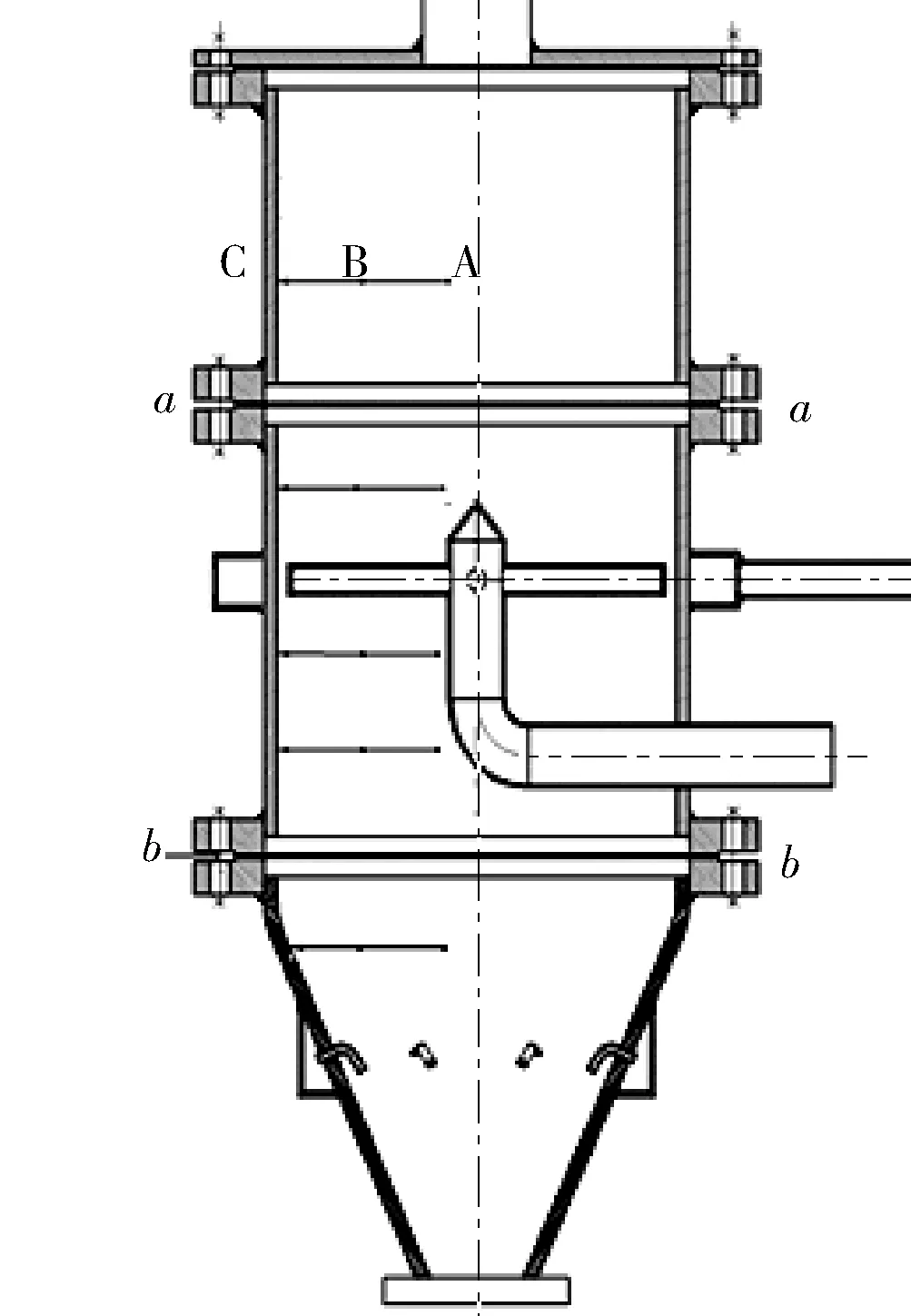
图1 炉体结构

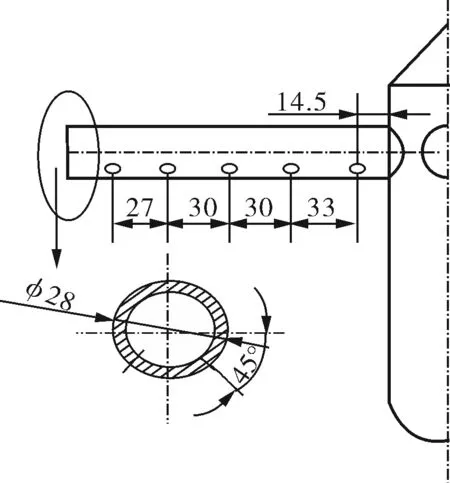
a. 中心进气

b. 边壁进气

根据干馏炉实际尺寸建立几何模型，并采用Gambit划分网格(图3)。网格为结构化与非结构化网格相结合，进气孔处的网格都进行局部加密，共计112 875个网格。根据炉体填料位置和物料在干馏炉的堆积特性，将模拟体域分为两个部分，上部(图1中炉顶至a-a线)为气流区域，下部(图1中a-a线至炉底)为多孔介质区域。

图3 网格划分

为了测量工作时干馏炉内堆积体各区域的温度参数，在炉体内部安装了多个温度传感器，这些传感器是经济实惠的K型热电偶。由于干馏段温度是影响实验结果最主要的因素，所以大部分热电偶集中布置在干馏段。炉内5个高度每个高度有3个温度测点，共15个，分布在堆积区域内，按与炉心的距离将测点分为A、B、C3组，测点位置和测点温度值见表1。

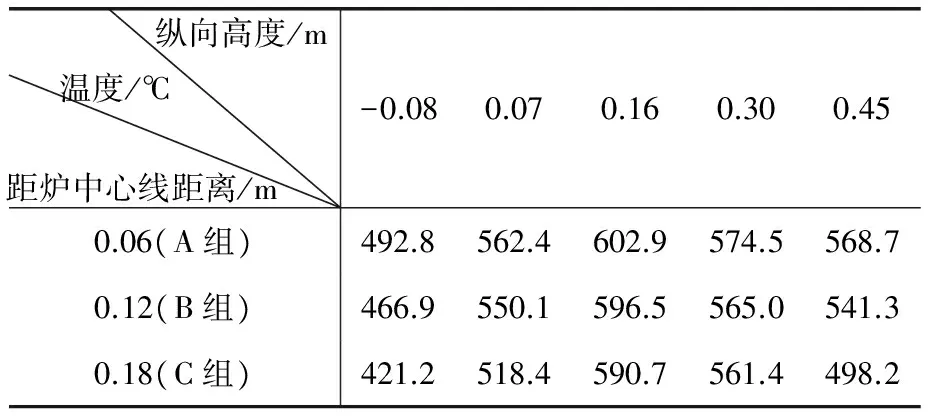
表1 实验中各测点和测点温度

2 数学模型

为合理地简化计算，更方便地应用Fluent软件模拟炉内的温度分布，给出以下假设：热解进行到一定程度时，干馏炉处于稳定状态，各参数不随时间改变；堆积的页岩为各向均匀的多孔介质，边壁处的空隙率无变化；内部与炉边壁间的换热完全为对流换热，各壁面换热系数分别给予某定值。

由于油页岩在干馏炉内的堆积特性，因此将油页岩区域设为多孔介质区域，并对多孔介质模型下物料反应对温度分布的影响进行UDF编程，热载气流动采用层流模型，整个炉体场内为导热模型。气体热载体在整个多孔介质腔道内为湍流的流动方式，而从两粒油页岩穿过的角度看流动偏向层流，因此，笔者采用层流模型与湍流模型对比的方法确定最佳模型设置。

2.1基本方程

油页岩热解的CFD模型包含对流动、传热传质和化学反应过程的描述，基本方程包括质量、动量、能量的守恒方程，分别为：

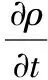
(1)

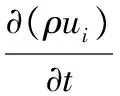
(2)

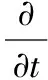
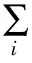
(3)

式中Ef——流体的总能量；

Es——固体的总能量；

kf——流体热导率；

ks——固体热导率；

Si——方程在i方向上的阻力源项；

Sm——源项。

2.2多孔介质模型

通常，考虑到固定床内流道几何形状极端复杂性，应用CFD研究的一种思路是把固定床视为一种等效的多孔介质或者采用拟均相假设[6]，发生在床层中的化学反应被处理成守恒方程的源项；将流体在多孔介质区域内的流动视为有特定附加源项的流动Si。通过在动量控制方程源项中增加多孔介质阻力项，模拟流体流经多孔介质区域时的动量损失。多孔介质模型主要的非线性微分方程在各向同性的简单均匀多孔介质区域中，可简化为[7]：

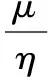
(4)

式(4)中的1/η和C2即为粘性阻力系数和惯性阻力系数，根据厄根方程可知，此两项的求解方程为：

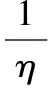
(5)

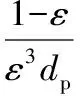
(6)

其中，ε为多孔介质的空隙率，dp为颗粒当量直径，A=150，B=1.75。

在Fluent软件中进行多孔介质域模拟时需要确定并输入这两个系数，以计算动量方程中的阻力源项。

2.3化学反应模型

油页岩热解是非均相的二级反应，包括3个方面[8]：油页岩干燥和水分析出；干酪根热解的气固非相反应；气体均相的二级反应。笔者将油页岩块粒设为多孔介质模型下的物料，除对它进行物性参数设置外，还要考虑油页岩热解反应吸热对温度分布的影响，若设置固定热源值代替，则要求反应程度的绝对性，很难达到，因此很有必要将化学反应吸热对温度分布的影响编程(即UDF方法)导入Fluent中计算，将结果进行表达。

对油页岩热解的研究很多，但目前没有统一油页岩的化学方程式和热解方程式，笔者基于对实验原料物性的研究，假设反应是一级反应，化学方程式如下[9]：

干酪根(油母质)→油+气+焦+残炭

(7)

对于固体均相反应，认为反应动力学因素控制反应进行，反应的反应速率可参考文献[10]开发的阿伦尼乌斯方程形式的化学反应动力学方程：

Rp1=(1-ε)Ap1·exp(-Ep1/RTavg)ρv

(8)

式中Ap1——热解的频率因子，1/s；

Ep1——热解活化能，J/mol；

Rp1——热解反应速率，kg/(m3·s)；

Tavg——固体平均温度，K；

ρv——挥发分的密度，kg/m3。

模型中化学反应的动力学参数[11]为：活化能Ep1=186kJ/mol，频率因子Ap1=1.88×1012s-1，反应吸热焓H=189.29 kJ/mol。

本研究模拟采用的原料是内蒙油页岩，对它进行工业分析，其中水分的质量分数是3.75%，挥发分是18.13%，灰分是69.98%，固定碳是8.14%。根据计算公式与油页岩热解所需的动力学参数等进行UDF[12]编程导入Fluent多孔介质模型下的计算模拟中，将化学反应对温度分布的影响表达出来。

2.4边界条件

速度入口根据总进气流量与进气孔面积、个数可确定流速为4.17m/s；炉内微负压出口为自然出口；各壁面均为无滑移，换热系数从report获得；因十字送风管内侧为流动热气，管道外侧为堆积物料，中心管布置在炉体内由于里面流动的是高温气体，在对外边壁的边界条件设置时，笔者进行了两种边界条件的假设对比：恒壁温与恒热流，其中根据热量与横截面积比确定热流量为4.85W/m2。

3 结果对比

3.1恒热流边界条件下的对比

当设置中心管的边界条件为恒热流时，图4a～c分别表示不同流动模型下z=0截面的温度分布，由图可知，3种流动模型温度分布大致为：由于接近入口，高温区集中在中心管四臂下方，且温度从高温区向炉顶与炉底均匀递减。图4b的SA湍流模型与图4c的RNG湍流模型温度云图相似，这是因为温度分布受中心管壁边界条件的影响较大，因此多孔介质模型作用下流动很相似，热载气体在整个多孔介质炉腔内湍流的假设论据不足。从纵向截面图对比发现：湍流模型比层流模型的最高温度高，在经过多孔介质模型时动能损失少；两者温度云图在干燥段和冷却段区别不大，即物料对流动的阻碍作用使热载气几乎流动不到这里，以导热为主同时反应进行程度不大。

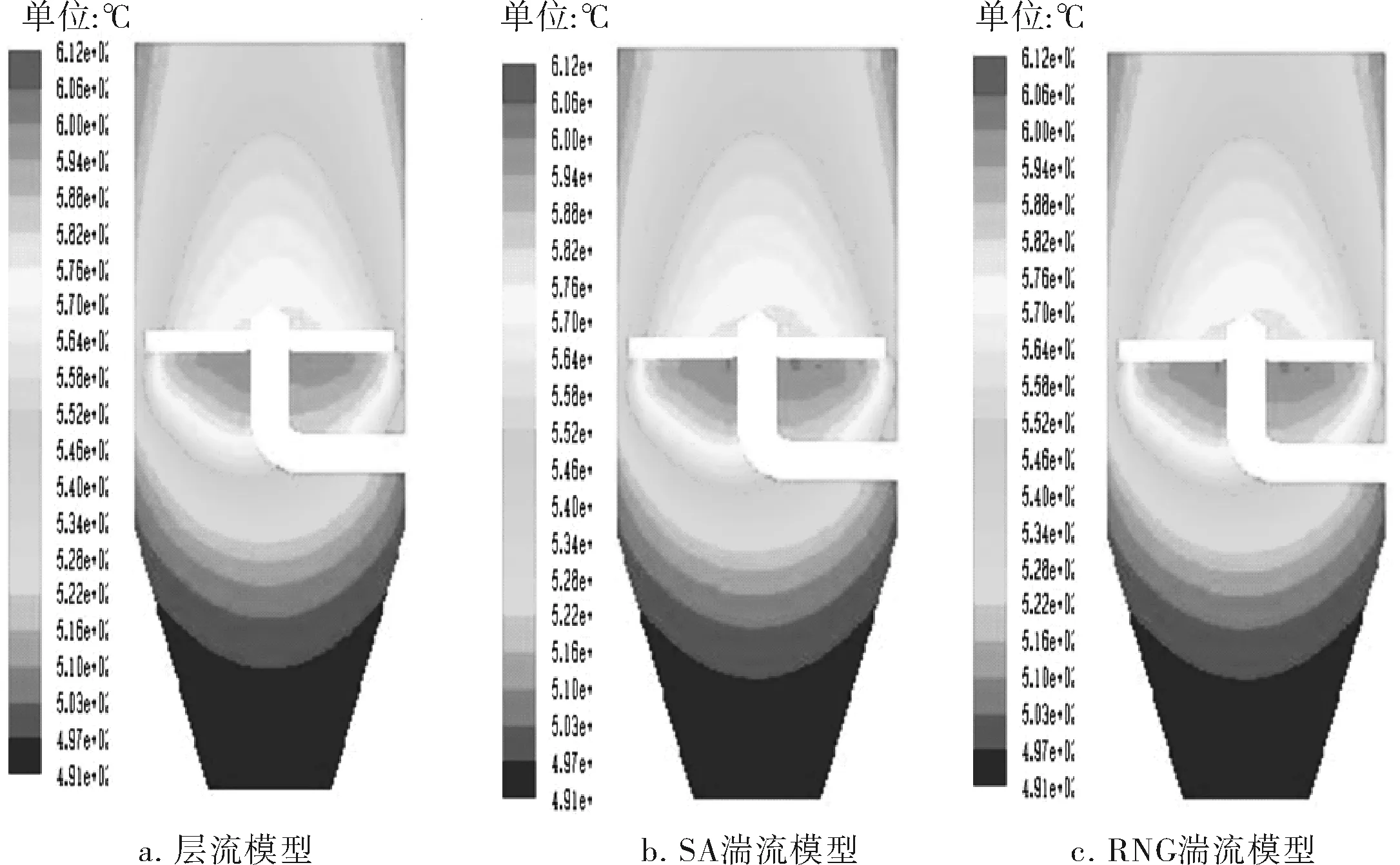
图4 恒热流边界条件下不同流动模型的温度分布

图5、6分别表示不同截面处层流模型与湍流模型的温度云图。图5a与图6a是y=0.05m处横截面温度云图，对比发现：两种模型的温度分布都较均匀且由中心向边壁递减，这种结果与进气方式有关，笔者采用的是中心边壁联合进气的方式，而y=0.05m处于进气口下方，温度主要受中心管壁条件的影响；同时，在中心管四壁正下方的y=0.05m处出现等温圈缺口，这是由于中心管壁布气孔处于斜下方45°(图2a)；层流模型的温度分布较湍流的高，这是层流湍流本质区别的体现，层流没有径向脉动，因此，热载气体在层流模型下的流动有深度少跨度。

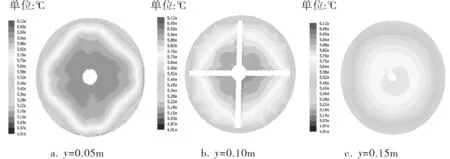
图6 湍流模型在不同位置截面的温度云图

图5b与图6b是y=0.10m处横截面温度云图，该位置极其接近中心管入口上方一点，速度在此方向上分量小，温度较y=0.05m处低，由于中心管的阻挡流动不稳定，因此可能会出现温度骤增或骤降。在选择不同的湍流模型时，流动带动温度分布，因湍流扰动性强，高温气体触及面积大；边壁进气使边壁附近温度升高，解决了热载气体到达不了、反应不彻底和降低转化率的弊端。图5c与图6c是y=0.15m处横截面温度云图，湍流模型结果中高温区域大，明显印证在多孔介质阻碍作用下湍流比层流动能损失少。同时湍流模型计算的结果低估了换热系数，温度梯度较层流模型的小。

温度分布在一定程度上反映了流动特性，从实验结果发现在中心管上方区域温度分布情况更趋近于层流模型下的结果，略不均匀、温度变化大。

3.2恒壁温边界条件下的对比

当设置中心管的边界条件为恒壁温时，图7表示不同湍流模型时z=0截面的温度分布，由图可知，恒壁温边界条件与恒热流边界条件模拟的温度分布相似，只是要比恒热流边界条件下的温度高，与实验结果不符是因为恒壁温使得热量具有堆积性，使中心管类似于固定热源，弱化了与周围的换热。

图7 恒壁温边界条件下不同流动模型结果

图8、9为不同截面处层流模型与湍流模型的温度云图，同样因热解的调节作用使得温度分布均匀，因多孔介质的阻碍作用温度递减，因流动模型不同高温区面积大小形状不同，层流模型比湍流模型的温度分布更均匀除却流动特性，最主要因为在计算结果上层流高估了换热系数而湍流却算低了换热系数，所以出现湍流较层流在y=0.05m处温度高的结果。

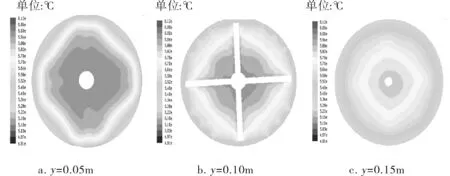
图8 层流模型在不同位置截面的温度云图

图9 湍流模型在不同位置截面的温度云图

恒壁温边界条件下的模拟仿真结果明显高于实验测量值，与实际不符，只是边界条件在一定程度上反映的是中心管内侧的换热情况，拓宽了研究的思路，可以根据中心管内的流动状态了解它在炉内的换热情况，最终达到优化中心管即优化炉内温度分布的目的。

3.3与实验结果对比

图10为炉内距中心A、B、C不同位置的纵向温度曲线对比图，每幅图中线B、D表示层流模型下的边壁恒温与恒热流，线F、H表示湍流模型下的边壁恒热流与恒温。由图发现湍流模型中在接近中心管上或下时都有温度骤增和骤降，且在接近壁面的C组实验中对比发现湍流模型较层流模型温度高，这些是判断层流模型与湍流模型的关键；从接近中心管的A组中对比发现不论层流湍流，不论恒热流恒壁温4条曲线的温度都很接近，说明化学反应程度相近，与实验数据也最相近，与B组结果相似随着位置升高各个模型下温度差别也越大，因此3组中编号4、5测点的温度是确定中心管壁边界条件的最佳数据。

a. A组数据对比 b. B组数据对比 c. C组数据对比

对比表1中的实验数据发现，实验数据较模拟值在中心处温度偏高边壁处偏低，这与反应进行程度和炉体散热有关，由C组数据对比确定层流模型，由A组数据对比并计算方差，其中在位置编号4、5测点处恒热流边界条件方差结果为：σ4=6.0K，σ5=12.6K。恒壁温方差为：σ4=8.6K，σ5=17.7K。因此确定此实验干馏实验炉最佳的模型为层流模型，中心管边界条件为恒热流。

4 结论

4.1实验数据与模拟结果对比，发现由于模拟将化学反应进行理想化彻底化，使得模拟结果中温度分布更均匀，且干馏段的温度要低于实验测量值。

4.2由于假设炉内油页岩是各向均匀的多孔介质，边壁处的空隙率无变化，温度由中心向边壁均匀递减，并且阻力系数设置影响流动与热量传递，在炉底处表达尤为明显，炉底温度涉及排渣问题，所以优化阻力系数或空隙率设置很有必要。

4.3基于边壁与中心送气的气体热载体干馏炉，模拟结果与实验数据均显示，由于边壁送风孔布置稀疏，仅在送风位置温度整体均匀一致，使得热解反应的发生率与反应程度更高，因此优化进气比、空隙率等参数的设置势在必行。

[1] 秦宏，张鑫，柏静儒，等. 油页岩气体热载体干馏炉内温度分布的试验研究[J].化工机械，2014，41(6)：727～732.

[2] 秦宏，张成，李建坡，等.气体热载体干馏炉内压力降的研究[J].东北电力大学学报，2015，35(1)：1～6.

[3] 秦宏，李建坡，王擎，等.油页岩气体热载体干馏炉内干馏特性研究[J].化学工程，2015，43(5)：11～15.

[4] 范贤振，郭烈锦，高晖，等.200MW四角切向煤粉炉炉内过程的数值模拟[J].西安交通大学学报，2002，36(3)：241～246.

[5] 邓中乙，肖睿，金保升，等.加压喷动流化床煤气化数值模拟[J].燃烧科学与技术，2009，15(4)：332～338.

[6] Nijemeisland M，Dixon A G.Comparison of CFD Simulations to Experiment for Convective Heat Transfer in a Gas-Solid Fixed Bed[J].Chemical Engineering Journal，2001，82(1)：231～246.

[7] 贝尔，竞生，崇希.多孔介质流体动力学[M].北京：中国建筑工业出版社，1983.

[8] 徐峰.油页岩热解及燃烧反应的化学动力学研究[D].吉林：东北电力大学，2007.

[9] Fausett D W.Proceedings of the 8th Oil Shale Symposium[J].Colorado School of Mines，1975，70(3)：273～313.

[10] Chan W C R，Kelbon M，Krieger B B.Modeling and Experimental Verifycation of Physical and Chemical Processes during Pyrolysis of a Large Biomass Particle[J].Fuel，1985，64(11)：1505～1513.

[11] 钱家麟，尹亮.油页岩——石油的补充能源[M].北京：中国石化出版社，2008.

[12] 韩占忠，王敬，兰小平.FLUENT流体工程仿真技术实例与应用[M].北京：北京理工大学出版社，2004.

TemperatureFieldSimulationandValidationinFurnaceofOilShaleRetortwithGasHeatCarrier

BAI Jing-ru, FENG Yan, XIN Si-yu, ZHANG Wei, WANG Qing, QIN Hong

(EngineeringResearchCentreoftheMinistryofEducationforComprehensiveUtilizationofOilShale,NortheastDianliUniversity,Jilin132012,China)

The gas retort has heat carrier and it boasts 400 mm in the diameter and 1 089 mm in the height and it has air supply from both center and side wall. The CFD-Fluent was adopted to simulate temperature field when the shale were distillated in the retort. Considering the fact that oil shale stacked hinders both flow and heat transfer, the zone within the retort was designed as porous medium model; and through having different flow models and boundary conditions—laminar flow model and turbulent model adopted, and having center air supply device’s constant wall heat flux compared with constant wall temperature condition, the optimal setting can be determined, the simulation results show that, the temperature field in longitudinal and transverse direction decreases progressively and different flow models bring about different temperature permeability; and different boundary conditions incur various degree of reaction and the expression of temperature uniformity. Compared with the experimental data indicates that, in the laminar flow model, the heat flux boundary condition of the central tube becomes more similar with the test results.

gas retort, oil shale, fixed bed, Fluent, porous medium

**柏静儒，女，1973年6月生，教授。吉林省吉林市，132012。

*吉林省重点科技攻关项目(20140204004SF)。

TQ054

A

0254-6094(2016)05-0665-07

2015-10-15，

2016-08-17)

声明

本刊已许可中国学术期刊(光盘版)电子杂志社在中国知网及其系列数据库产品中以数字化方式复制、汇编、发行、信息网络传播本刊全文。该社著作权使用费与本刊稿酬一并支付。作者向本刊提交文章发表的行为即视为同意我刊上述声明。