烟气轮机叶材高温冲蚀建模及分析

任琪琛

(兰州理工大学石油化工学院)

烟气轮机叶材高温冲蚀建模及分析

任琪琛*

(兰州理工大学石油化工学院)

塑性金属的冲蚀磨损是磨粒微切削和变形疲劳磨损的共同作用。建立了一种新的基于微切削和变形磨损的可用于高温环境的冲蚀率模型，采用积分计算了磨粒微切削造成的靶材磨屑体积，依据局部化模型和低周疲劳推导出变形磨损的表达式，分析了冲角和温度对冲蚀磨损率的影响。结果表明：GH864发生最大冲蚀率的冲角在50°左右；GH864的冲蚀率在低冲角(30、50°)下随温度的升高而增加，550℃以后增加缓慢，高冲角(90°)下在常温至400℃间几乎不变，400℃以后大幅减小；温度的升高会增加切削磨损，但减小变形磨损，不同温度下流动应力、动态硬度和临界应变的变化对冲蚀特性影响很大。

塑性金属 冲蚀 冲角 高温 微切削 变形

冲蚀磨损是指材料受到流动粒子冲击时表面出现破坏的一类磨损现象[1，2]，英国科学家Eyre T S认为冲蚀磨损占工业生产磨损破坏总数的8%[3]，它对催化裂化能量回收的烟气轮机(以下简称烟机)叶片危害巨大。烟机高温烟气中的催化剂颗粒高速冲击叶片会造成严重的冲蚀磨损，不仅会降低叶片的强度，而且会改变烟气流道、恶化流动工况、降低效率，甚至引起停车事故。

国内外专家学者不断从不同方面对冲蚀磨损进行研究，取得了很多理论成果，如Finnie I的微切削理论[4]、Bitter J G A的变形磨损理论[5]、林福严和邵荷生根据临界塑性变形应变量提出的低周疲劳冲蚀理论[6]，但对于实际情况中烟机叶材冲蚀磨损的预测都有很大的局限性。之后的研究者们主要集中于冲蚀磨损的数值模拟[7，8]和实验研究[9]，未能就理论模型进行修正或改良。

基于上述研究现状，笔者依据磨粒的微切削和材料变形磨损建立了一种适用于烟气轮机高温环境的镍基合金冲蚀磨损模型，将磨粒对靶材的冲蚀磨损分为微切削和变形磨损两部分，即磨粒在水平方向切削靶材，在垂直方向多次压缩靶材塑性变形造成变形磨损。因镍基高温合金具有优良的抗氧化和腐蚀特性，暂不考虑烟气氧化和腐蚀对叶片冲蚀的加速作用，将会在以后的工作中予以修正。

1 切削磨损

材料冲蚀是磨粒、靶材性质、冲击速度、冲角及环境等多因素的综合影响结果[10]。为方便分析问题，将磨粒冲击靶材的接触等效为一个弹塑性平面和一个刚性球体的接触，如图1所示，Ⅰ区表示由于磨粒微切削造成的磨屑，Ⅱ区为磨粒冲击靶材造成的塑性变形区。由于磨粒与靶材接触时间极短，故假设磨粒与靶材接触面与陷坑重合。

图1 磨粒与靶材接触示意图

1.1弹性变形阶段

磨粒刚开始接触靶材，靶材处于弹性变形阶段，根据赫兹接触理论[11]，法向接触力F为：

(1)

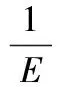
式中E1——靶材的弹性模量；

E2——磨粒的弹性模量；

h——靶材的冲击变形量；

R——刚性球形磨粒半径；

ν1——靶材的泊松比；

ν2——磨粒的泊松比。

根据能量守恒原理，磨粒在垂直方向的运动速度随变形量的增大而减小，即：

(2)

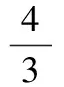
式中m——单个磨粒质量；

V——磨粒的初始速度；

V⊥——磨粒在垂直方向挤压靶材的速度；

θ——磨粒冲角；

ρ1——磨粒密度。

由式(2)可得：

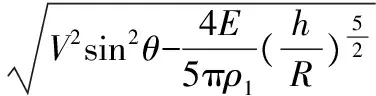
(3)

由于和靶材接触面之间存在摩擦，则磨粒在水平方向的运动速度V∥为：

(4)

式中f——弹性阶段磨粒与靶材的滑移摩擦系数；

t——磨粒与靶材的接触时间。

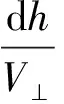
V∥=V(cosθ-fsinθ)+fV⊥

(5)

在该阶段中，磨粒冲击靶材后只有弹性变形，无冲蚀磨损出现。

1.2塑性变形阶段

在塑性压入过程中靶材以恒定的应力阻止磨粒，其值可取为材料的动态硬度[12]。根据赫兹接触理论，弹性接触状态下的最大应力Pmax为：

(6)

当磨粒冲击靶材的最大应力达到材料动态硬度Pd时，靶材开始进入塑性变形状态，即：

Pmax=Pd

(7)

由式(6)、(7)得到靶材的由弹性变形转为塑性变形的临界变形量hc为：

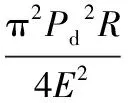
(8)

当冲击变形量hhc时，靶材处于弹塑性变形阶段，即靶材变形量大于hc的部分塑性屈服，小于hc的部分仍然处于弹性压缩，如图2所示。只有磨粒冲击靶材使它处于塑性变形时才能在水平方向切削靶材[13]。

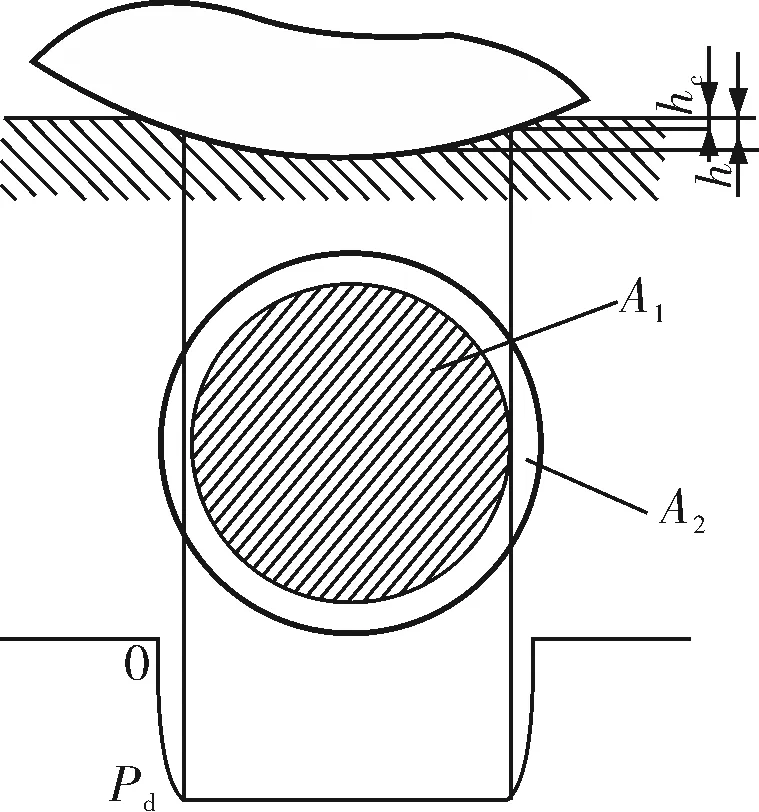
图2 磨粒靶材弹塑性接触时的变形量、接触面积和接触应力分布示意图

当靶材处于塑性变形阶段时，磨粒在垂直方向受到塑性变形部分变形抗力的作用，受力面积A1为：

A1=2πR(h-hc)

(9)

在垂直方向受到弹性变形区域弹性力的作用，受力面积A2为：

A2=2πRhc

(10)

弹性接触时的平均应力P为最大接触应力的2/3倍，则磨粒的法向接触力F为：

(11)

磨粒的挤压速度逐渐减小，则：

(12)

式(12)中V⊥(hc)表示在靶材变形量为hc时磨粒垂直方向的挤压速度，下同。

将式(10)代入式(12)可得：

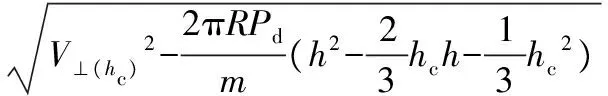
(13)

当磨粒挤压速度减小到零时，靶材达到最大变形量H为：

(14)

磨粒在水平方向受到切削抵抗力的作用，受力面积为：

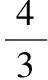
(15)

磨粒的切削速度也逐渐减小，则：

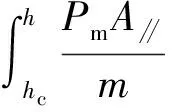
(16)

式中Pm——材料流动压力。

陈大年等指出冲蚀切削的应力为[14]：

Pm=Kσy

(17)

其中，σy是材料的极限屈服应力，刚塑性材料在发生塑性接触时，K=2.8～3.2。

(18)

磨粒切削靶材的体积S1为：

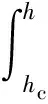
(19)

将式(13)、(15)、(18)代入式(19)，可得：

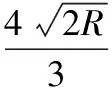
(20)

若在该阶段中水平切削速度变为零，则式(20)中h取为H0，且V∥(H0)=0；否则h取为H。

1.3弹性恢复阶段

磨粒在靶材垂直方向的弹性变形恢复力的作用下被挤出，且在水平方向继续切削靶材，此时磨粒在垂直方向的速度随变形的恢复逐渐增大，即：

(21)

式(21)转化为微分方程求解得：

(22)

靶材的弹性恢复变形量只有hc，故式(22)中h≥H-hc。而在水平方向的切削速度仍然在切削抵抗力的作用下不断减小，即：

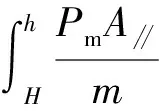
(23)

将式(15)、(22)代入式(23)得：

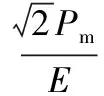
(24)

磨粒切削靶材的体积S2为：

(25)

将式(15)、(22)、(24)代入式(25)，得：

(26)

若在该阶段中水平切削速度变为零，则式(26)中h取为H1，且V∥(H1)=0；否则h取为H-hc。

磨粒在靶材弹性恢复力作用后垂直速度在忽略重力等因素情况下保持不变，磨粒继续切削靶材，则水平速度为：

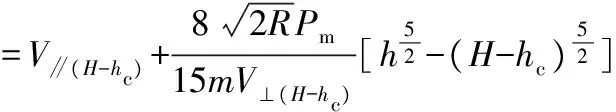
(27)

此时，磨粒的切削体积为：

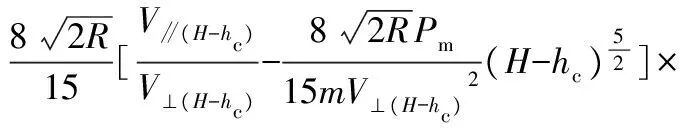
(28)

若在该阶段中水平切削速度变为零，则式(28)中h取为H2，且V∥(H2)=0；否则h取为hc。

综上所述，磨粒与靶材接触的运动过程中总的切削磨屑体积S为：

S=S1+S2+S3

(29)

2 低周疲劳磨损

单磨粒在垂直方向上冲击挤压靶材会引起塑性变形，而磨粒的连续冲击将导致靶材的变形磨损[15]，即材料表面被磨粒的单次冲击后发生一定程度的应变，当多次磨粒冲击后材料的应变积累达到“临界应变”时，会造成塑性变形区域内材料的迁移。

磨粒的冲击动能主要消耗于材料的弹性变形和塑性变形，则根据Tabor理论[16]，磨粒单次冲击靶材的塑性变形区域体积W为：

W=πR(H2-hc2)

(30)

若未发生塑性变形，则W=0。

球形磨粒最终压入靶材的塑性变形半径a为：

(31)

为简化，单个磨粒压入靶材时整个塑性变形体积的平均应变增量Δep为：

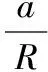
(32)

文献[17]指出最终造成塑性变形体积完全迁移的冲击次数Nf为：

(33)

并表明式(30)中材料的临界塑性应变ef为常规强度试验时达到破坏的应变值。但林福严和邵荷生指出实际冲蚀磨损过程中，应变率一般很高，通常发生绝热剪切，导致变形局部化，故ef应是变形局部化临界应变[6]。根据Sadararajan G和Shewmon P G的局部化模型理论得出变形局部化的临界应变[18]：

(34)

式(34)中n为靶材的应变硬化指数，ρ2为靶材的密度，Cp为靶材的比热容，C为靶材的剪切模量温度系数，p=1/(n+1)，K为靶材的强化系数，K=0.3Hs，Hs为靶材的静态硬度。

3 总冲蚀磨损率

由以上分析可知，单颗粒的冲蚀磨损率ε为：

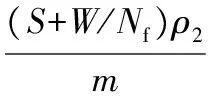
(35)

Finnie I指出，实际情况中多颗粒冲击靶材时只有部分颗粒参与微切削，取比例为α，故多颗粒冲蚀磨损率为[4]：

(36)

4 理论模型验证及影响因素分析

高温镍基合金GH864(waspaloy)是烟机叶片的常用材料[19]，工作环境常在600～800℃，故根据以上模型研究它在高温下冲蚀磨损特性。GH864的材料特性随温度变化见表1～4。

表1 不同温度下GH864的弹性模量

表2 不同温度下GH864的动态硬度[20]

表4 不同温度下GH864的比热容

为了更好地预测烟机叶片在高温下的冲蚀特性，将GH864的弹性模量、动态硬度、屈服强度、比热容拟合为关于温度的函数，即：

E(T)=-4.8142×10-8T3+3.7354×10-5T2-

0.0711T+225.5079

(37)

Pd(T)=-3.1546×10-9T3+7.2285×10-6T2-

0.0062T+5.0524

(38)

σy(T)=-2.8485×10-6T3+0.0018T2-0.3339T+

1285.8

(39)

Cp(T)=-7.6652×10-6T2+0.319T+399.4747

(40)

4.1冲角对冲蚀率的影响

Shanov V等在538℃环境温度下实验获得了不同冲角铬铁矿颗粒305m/s冲击waspaloy的冲蚀率[21]，笔者以它为例进行验算(图3)。比较发现GH864表现了典型的塑性金属冲蚀特性，最大冲蚀率发生在50°左右，在低冲角时本模型预测值比实验值略小，在高冲角时与实验值吻合较好，这是因为低角度时冲蚀磨损主要来源于磨粒切削，实验中的磨粒为多角颗粒，会造成较大的切削量[22]，而高角度时靶材冲击变形逐渐增大，冲蚀磨损以变形磨损为主，所以笔者建立的冲蚀率计算模型是可信的，可用于GH864的高温冲蚀磨损的预测。同时也可以看出磨粒形状对切削磨损有较大影响，对变形磨损影响不大。

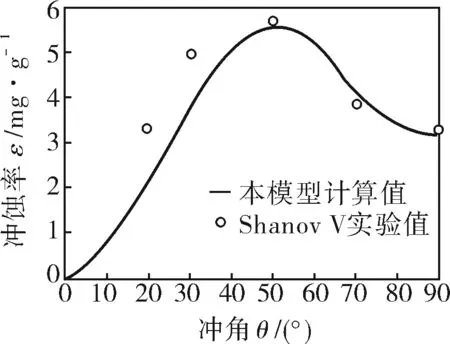
图3 实验值与预测值的比较

4.2环境温度对冲蚀率的影响

催化裂化中催化剂颗粒的主要成分是Al2O3，在烟气中的最高速度在200m/s以上，假设粒径为15μm，研究不同温度下GH864的临界变形量、最大变形量、造成塑性变形体积完全迁移的冲击次数的变化情况，如图4～6所示。可以看出hc先随温度的增大而减小，600℃以后随温度增大而增大但变化不大，即温度越高GH864越易发生塑性变形但在烟机叶片工作温度下基本变化不大；H随温度的增加而增大，即温度越高GH864的塑性变形越大；Nf随温度的增大而增大，特别在750℃以后迅速增加，说明温度的升高对于减小变形磨损是有利的。

图4 临界变形量hc与温度的关系

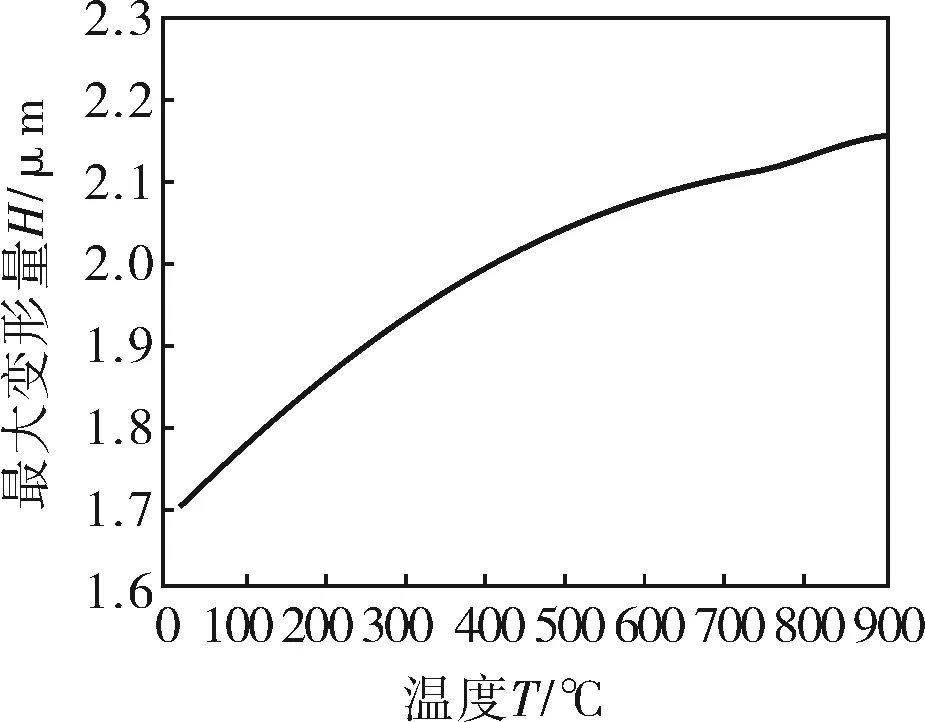
图5 最大变形量H与温度的关系

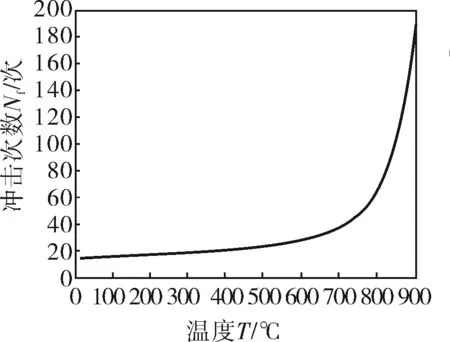
图6 冲击次数Nf与温度的关系

根据烟机的实际工况预测了30、50、90°冲角下冲蚀率随温度的变化，如图7所示。可以看出高温下GH864的冲蚀率50°最大，30°次之，90°最小；30°和50°冲角下冲蚀率随温度增加而增加，在550℃后增速减缓，这主要是由流动应力和动态硬度的变化所影响的；90°冲角下的冲蚀率在常温至400℃间几乎不变，400℃以后大幅减小，这是高温下GH864的临界应变(或造成材料迁移的冲击次数)迅速增大所导致的。即烟气温度的升高会增加催化剂颗粒对叶片的切削磨损却可以使变形磨损减小，叶材的流动应力、动态硬度和临界应变对冲蚀特性影响很大[23]。

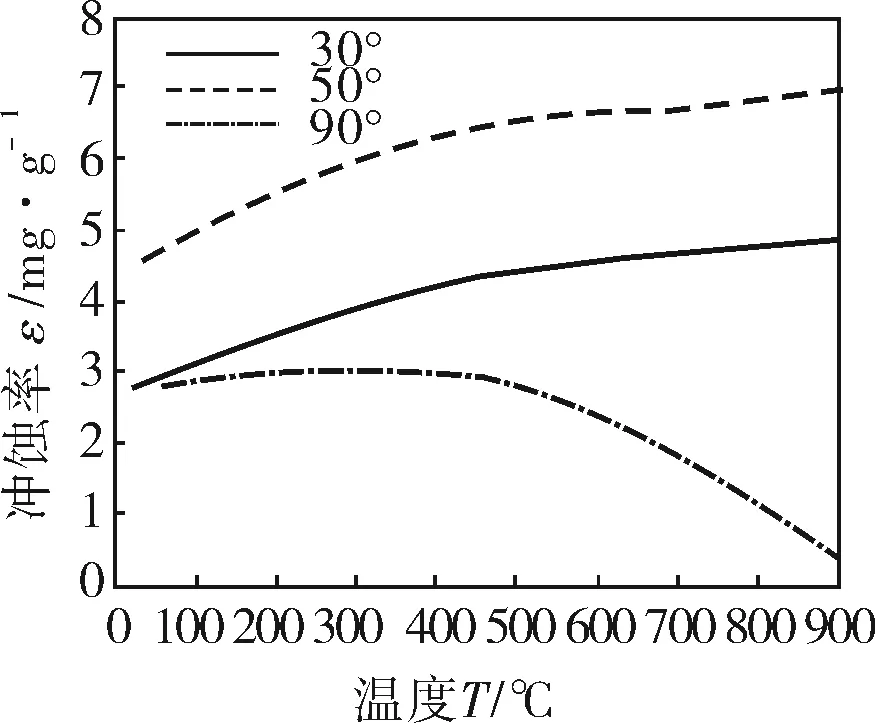
图7 3种冲角下冲蚀率ε与温度的关系

5 结论

5.1建立了一种新的基于微切削和变形磨损的可用于高温环境的冲蚀率预测模型，经验证具有很好的准确性。

5.2GH864表现了典型的塑性金属冲蚀特性，发生最大冲蚀率的冲角在50°左右。

5.3GH864的临界变形量随温度的增大而减小，在600℃以后略有增加但变化不大，最大变形量随温度增大而增大，造成塑性变形区域材料迁移的冲击次数在750℃以后迅速增加。

5.4GH864的冲蚀率在低冲角(30、50°)下随温度的升高而增加，550℃以后增加缓慢；高冲角(90°)下在常温至400℃间几乎不变，400℃以后大幅减小。

5.5温度的升高会增加切削磨损，但也可使变形磨损减小，不同温度下流动应力、动态硬度和临界应变的变化对冲蚀特性影响很大。

5.6高温冲蚀磨损是复杂的多因素问题，以后需在此基础上以烟气轮机实际工况为准进行实验，以完善冲蚀模型。烟气轮机的复杂流场对催化剂颗粒冲蚀叶片影响很大，烟气中的SO2、O2等介质对叶片的氧化腐蚀作用会加速冲蚀磨损，今后要将这些因素对冲蚀的影响加以考虑。

[1] 董刚，张九渊.固体粒子冲蚀磨损研究进展[J].材料科学与工程学报，2003，21(2)：307～312.

[2] 郭源君，王永岩，庞佑霞，等.材料的冲蚀疲劳研究[J].振动与冲击，2004，23(2)：37～38，17.

[3] Eyre T S.Treatise on Materials Science and Technology[J].Wear，1979，13：363.

[4] Finnie I.Some Reflections on the Pastand Future of Erosion[J].Wear，1995，186：1～10.

[5] Bitter J G A.A Study of Erosion Phenomena[J].Wear，1963，6(1)：5～21.

[6] 林福严，邵荷生.冲蚀磨损理论模型的研究[C].磨损理论与抗磨技术.北京：科学出版社，1993：96～101.

[7] Liu Z G，Wan S，Nguyen V B，et al.A Numerical Study on the Effect of Particle Shape on the Erosion of Ductile Materials[J].Wear，2014，313(1/2)：135～142.

[8] 谢文伟，邓建新，周后明，等.材料冲蚀磨损的数值模拟研究现状及展望[J].腐蚀与防护，2012，(7)：601～604.

[9] Nsoesie S，Liu R，Chen K Y，et al.Analytical Modeling of Solid-particle Erosion of Stellite Alloys in Combination with Experimental Investigation[J].Wear，2014，309(1/2)：226～232.

[10] Aminul Islam Md，Farhat Z N.Effect of Impact Angle and Velocity on Erosion of API X42 Pipeline Steel under High Abrasive Feed Rate[J].Wear，2014，311(1/2)：180～190.

[11] Johnson K L.Contact mechanics[M].Cammbrige：Cammbrige University Press，1985.

[12] Sundararajan G.Understanding Dynamic Indentation Behaviour of Metallic Materials[J].Materials Science and Technology，2012，28(9/10)：1101～1107.

[13] 李诗卓，董祥林.材料的冲蚀磨损与微动磨损[M].北京：机械工业出版社，1984：61～68.

[14] 陈大年，Al-Hassani S T S，陈建平，等.固粒击靶的有效摩擦系数[J].工程力学，2004，21(5)：172～177.

[15] 王锦文，瞿伟廉.结构钢杆件基于变形和耗能的塑性破坏准则研究[J].振动与冲击，2013，32(19)：71～75.

[16] Tabor D.The Hardness of Metals[M].Oxford：Clarendon Press，1957.

[17] 孙家枢.金属的磨损[M].北京：冶金工业出版社，1992：440～520.

[18] Sundararajan G，Shewmon P G.A New Model for the Erosion of Metals at Normal Incidence[J].Wear，1983，84(2)：237～258.

[19] 胡燕慧，田永江，陈赤囡，等.激光熔覆修复的GH864合金烟气轮机动叶片失效原因分析[J].金属热处理，2008，33(5)：96～99.

[20] Chinnadurai S，Bahadur S.High-Temperature Erosion of Haynes and Waspaloy：Effect of Temperature and Erosion Mechanisms[J].Wear，1995，186/187：299～305.

[21] Shanov V，Tabakoff W，Gunaraj J A.Erosion Behavior of Uncoated Waspaloy and Waspaloy Coated with Titanium Carbide[J]. Surface and Coatings Technology，1997，94/95(1/3)：64～69.

[22] 马颖，任俊，李元东，等.冲蚀磨损研究的进展[J].兰州理工大学学报，2005，31(1)：21～25.

[23] Sundararajan G.The Solid Particle Erosion of Metallic Materials：The Rationalization of the Influence of Material Variables[J].Wear，1995，186/187：129～144.

ModelingandAnalysisofHigh-temperatureErosionofFlueGasTurbineBladeMaterials

REN Qi-chen, DING Xue-xing, ZHANG Wei-zheng, ZHANG Zheng-tang

(CollegeofPetrochemicalEngineering,LanzhouUniversityofTechnology,Lanzhou730050,China)

The co-action of micro-cutting and deformation erosion can incur abrasive erosion of plastic metals．An erosion rate model which based on micro-cutting and deformation erosion and applicable to high-temperature environments was established．The integral computation was applied to calculate the micro-cutting-incurred volume loss of the target material; basing on localization model and low-cycle fatigue, the expression of de-

*任琪琛，男，1990年8月生，硕士研究生。甘肃省兰州市，730050。 丁雪兴 张伟政 张正棠

TQ050.4+1

A

0254-6094(2016)05-0649-07

2015-09-22，

2016-08-17)

(Continued on Pge 684)