偏心和转速对汽轮机隔板汽封泄漏量的影响*

曹丽华 李 超 李 盼

(东北电力大学能源与动力工程学院)

偏心和转速对汽轮机隔板汽封泄漏量的影响*

曹丽华**李 超 李 盼

(东北电力大学能源与动力工程学院)

应用RNGk-ε湍流模型，基于有限体积法求解三维可压缩雷诺时均N-S方程，模拟分析了当转子存在偏心时，偏心距和转速对汽轮机隔板汽封泄漏量的影响。结果表明：在相同汽封间隙下，一定程度的偏心内，泄漏量随偏心距的增加而增加，达到最大值后泄漏量逐渐减小并趋于不变；在偏心和非偏心工况下，隔板汽封泄漏量在一定转速内皆随着转速的增加而降低。

汽轮机 隔板汽封间隙 偏心距 转速 泄漏量

汽轮机级内静叶隔板与转子之间存在一定的间隙，当蒸汽流过静叶通道，静叶前后的压差将促使一部分流体流进隔板间隙，形成泄漏流进而造成泄漏损失，降低汽轮发电机组的发电效率[1]。现代汽轮机逐步向高参数发展[2]，而当汽轮机转子存在偏心时，在隔板汽封内由于周向间隙的不对称分布，将对隔板汽封间隙内流动造成一定的影响。

Hirano T等对比分析了两种不同CFD软件对汽封流场的模拟效果，证明了运用数值模拟方法分析汽封内流动的可行性[3]。Vakili A D等采用二维模型，利用数值模拟方法得到了高低齿迷宫式密封泄漏流的流动特性和总压损失机理[4]。Bozzi L等通过数值模拟与实验对比，证明了间隙改变对汽封内流动有着显著的影响[5]。Rosenberg S S指出在迷宫密封内，转速较小时摩擦效应起主要作用，转速较高时则以惯性力为主[6]。丁学俊等利用Fluent软件，对不同结构迷宫密封的内部流动和泄漏特性进行了对比和分析[7]。张为荣和王强对建立的光轴平齿汽封模型进行了数值模拟，结果表明汽封的诸多结构参数中，间隙对泄漏的影响最大[8]。

然而，上述研究均未考虑转速对汽封流场的影响，而且在结构和运行工况上，与汽轮机迷宫密封相比，都存在一定的差异。由于汽封间隙很小，汽轮机的高速旋转会对汽流产生一定的离心作用，必然会对漏汽量产生影响。李军等指出，转子的旋转作用在对隔板汽封流场的分析中不能忽视[9]。周国宇等通过数值模拟与实验对比的方法，得出在转速较小的情况下转子无偏心时，转动对高低齿迷宫密封的影响很小[10]。曹丽华等采用数值模拟方法得到，汽轮机转子旋转使得隔板汽封的漏汽量与静止时相比较大[11]。

笔者从分析汽轮机隔板汽封间隙泄漏流入手，采用CFD软件对汽轮机高压缸第2压力级的高低齿隔板汽封进行数值研究，分析转子存在静偏心时汽封间隙和转子转速对隔板汽封泄漏量的影响，从而为汽轮机设计人员提供一定的理论参考。

1 计算模型和数值方法

1.1计算模型

计算模型选用的是某国产300MW汽轮机高压缸第二压力级的隔板汽封，其结构示意图如图1所示。

图1 迷宫式隔板汽封的结构示意图

具体参数如下：

齿数n10个

密封间隙s0.1～0.5mm

齿厚i0.3mm

凸台高度h2.4mm

齿间距a3.0mm

齿间距b4.2mm

凸台宽度w9mm

1.2基本控制方程

计算区域内的稳态三维流体动力学通用控制方程为：

div(ρuφ)=div(Γφgrandφ)+Sφ

式中Sφ——广义源项；

φ——通用变量，可表示u、v、t、k及ε等求解变量；

Γφ——广义扩散系数；

ρ——流体密度。

湍流模型选用的是修正湍流粘度的RNGk-ε模型，相比于标准的k-ε方程，RNGk-ε模型对于强旋流或者带有弯曲壁面的流动计算具有更准确的计算结果。压力和速度耦合采用Simple算法。方程的离散项采用二阶迎风差分格式。

1.3网格和边界条件

笔者采用整周隔板汽封模型计算汽封内泄漏流的特性。通过分块划分，保证结构化网格的质量。为了提高计算精度，对汽封流域内近壁面进行边界层加密。具体的网格划分情况如图2所示。

图2 网格划分

为了将网格数量对计算结果的影响降到最低，笔者进行了网格无关性验证，发现网格数量超过600万后计算结果变化趋势逐渐减小，超过700万后基本不变，因此可认为超过700万后网格数对计算结果的影响很小。最终确定不同模型的计算网格数在700万～750万之间。

工质采用高温高压可压缩的过热水蒸气。计算区域进口设为压力入口，出口设为压力出口，入口给定总压强10.7MPa，总温度744.1K，出口压力10.0MPa。旋转轴设为固体壁面，模型绕转子中心旋转。非动面设为绝热的无滑移壁面。为了提高模拟结果的准确性，在近壁面处采用壁面函数法。

2 计算结果与分析

2.1间隙对泄漏量的影响

当转子无偏心时，选取不同间隙的隔板汽封模型进行数值模拟。当额定转速为3kr/min时，汽封间隙与泄漏量的关系曲线如图3所示。可以看出，在给定工况下，隔板汽封间隙为0.1mm时蒸汽泄漏量最小为0.400kg/s；随着隔板汽封间隙的增加，泄漏量在逐渐变大，当隔板汽封间隙为0.4mm时，蒸汽泄漏量达到1.160kg/s。

图3 汽封间隙与泄漏量的关系曲线

在给定进出口条件下，额定转速为3kr/min时，隔板汽封腔室内压力的变化情况如图4所示。可以看出，压力从左向右依次降低，密封齿与转动部分构成多个间隙狭窄的齿缝，当汽体通过齿缝时压力加速降低，通过密封齿的逐级作用，最后使压力趋于压力出口值。

由图4可以得到密封的轴向压力分布，并且可知压降主要发生在齿顶间隙处，而在每个空腔内的压力变化并不大。当汽体由间隙流入空腔时，由于流域面积突然增加而形成强烈的漩涡，导致汽流动能损耗较多并转变成热能。而汽封间隙越小，汽封齿两侧的压差越大，汽封齿的节流效果越明显。因此，当隔板汽封在相同的边界条件下时，隔板汽封间隙越小，泄漏量越小。

图4 隔板汽封腔室内压力的变化情况

2.2偏心对泄漏量的影响

在相同边界条件下，隔板汽封间隙的变化会引起泄漏量的变化。当转子存在偏心时，隔板汽封间隙沿着周向发生变化，间隙较大的一侧泄漏量增加，而间隙较小的一侧泄漏量减小。

在给定进出口边界条件下，当额定转速为3kr/min时，不同汽封间隙下泄漏量与偏心距的关系曲线如图5所示。可以看出，当汽封间隙为0.2mm、偏心距为0.02mm时，隔板汽封泄漏量为0.602kg/s；随着转子偏心距的增加，隔板汽封泄漏量逐渐增大，此过程中间隙较大一侧的泄漏量起主导作用；当偏心距达到0.06mm时，泄漏量达到最大值0.649kg/s；当偏心距超过0.06mm后泄漏量略有下降；当偏心距为0.08mm时，泄漏量为0.641kg/s；而后随着偏心距的增加，泄漏量基本不变，此时间隙较大一侧泄漏量的增加值与间隙较小一侧泄漏量的减少值大致相同。同理，根据隔板汽封间隙为0.3、0.4、0.5mm时的模拟结果，可得到类似的规律。在相同汽封间隙下一定程度的偏心内，泄漏量随着偏心距的增加而增加，达到最大泄漏量后逐渐稳定；而当偏心距相同时，汽封间隙越小泄漏量越小。

图5 额定转速下泄漏量与偏心距的关系曲线

2.3转速对泄漏量的影响

保持入口压力10.7MPa、温度744.1K、出口压力10.0MPa不变，当转子偏心距为0.04mm时，不同汽封间隙下，泄漏量与转速的关系曲线如图6所示。可以看出，不同间隙下隔板汽封泄漏量均随着转子转速的升高而降低。这是因为转子旋转带来的旋转效应使得泄漏流在隔板汽封内伴随转子沿周向旋转，随着转速的升高，旋转效应就越显著，从而，隔板汽封泄漏量随着转子转速的升高而降低。

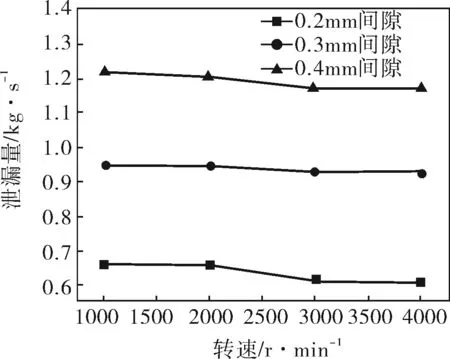
图6 泄漏量与转速的关系曲线

在给定进出口边界条件下，隔板汽封间隙为0.3mm，转子无偏心和偏心距为0.04mm时，泄漏量与转速的关系曲线如图7所示。可以看出，当转子在偏心工况和非偏心工况下时，泄漏量均随着转速的升高而降低。转速较小时，汽封内汽体的摩擦效应起主要作用，当转子存在偏心时隔板汽封的周向间隙发生变化，因汽体的摩擦作用，泄漏流在转子旋转带动下沿周向旋转，并在旋转方向上泄漏流带入间隙逐渐缩小的区域被压缩，进而在间隙逐渐扩散的区域处扩张，加快汽流动能损耗，因此使得在转速较小时相同工况下，转子存在偏心时的泄漏量更小。而随着转子转速的升高摩擦效应减弱，当转子在偏心距为0.04mm，转速较高时，泄漏更多地受到周向间隙不均的影响，间隙较大一侧泄漏量的增加起主导作用，此时转子存在偏心时的泄漏量较大。

图7 不同偏心距时泄漏量与转速的关系曲线

3 结论

3.1在额定转速下高低齿隔板汽封内，压力在汽封腔室内沿轴向逐渐降低。压降主要发生在齿顶间隙处，并且当汽封间隙增加时隔板汽封的泄漏量也增加。

3.2在额定转速下转子存在静偏心时，对于高低齿隔板汽封，相同汽封间隙下一定程度的偏心内，泄漏量随偏心距的增加而增加，泄漏量达到最大值后逐渐趋于不变。

3.3当偏心距不变时，高低齿隔板汽封的泄漏量随着转速的增加而降低，并且与非偏心工况相比，偏心时隔板汽封的泄漏量受转速影响较大。

[1] 叶建槐,刘占生.高低齿迷宫密封流场和泄漏特性CFD研究[J].汽轮机技术,2008,50(2):81～84.

[2] 魏琳健,李春清,高雷,等.汽轮机密封技术的应用和发展[J].热能动力工程,2005,20(5):455～458.

[3] Hirano T,Guo Z,Kirk R G.Application of Computational Fluid Dynamics Analysis for Rotating Machinery-Part II: Labyrinth Seal Analysis[J].Journal of Engineering for Gas Turbines & Power,2005,127(4):820～826.

[4] Vakili A D,Meganathan A J,Michaud M,et al.An Experimental and Numerical Study of Labyrinth Seal Flow[C].ASME Turbo Expo 2005:Power for Land,Sea,and Air.Reno:ASME,2005:1121～1128.

[5] Bozzi L,D′Angelo E,Facchini B,et al.Experimental Investigation on Leakage Losses and Heat Transfer in a Non Conventional Labyrinth Seal[C].ASME 2011 Turbo Expo:Turbine Technical Conference and Exposition.Vancouver:ASME, 2011:955～965.

[6] Rosenberg S S.Investigating Aerodynamic Transverse Forces in Labyrinth Seals in Cases Involving Rotor Eccentricity(Rotor Precession in Steam Turbines)[J].Energomashinostroenie,1974,8(8):15～17.

[7] 丁学俊,杨彦磊,肖国俊,等.迷宫密封流场与泄漏特性研究[J].流体机械,2006,34(4):14～18.

[8] 张为荣,王强.汽封流场及泄漏特性的数值模拟分析[J].汽轮机技术,2008,50(2):98～99.

[9] 李军,李国君,丰镇平.汽轮机光轴迷宫式隔板汽封内部流场的数值模拟[J].动力工程学报,2005,25(3):321～324.

[10] 周国宇,王旭东,林智荣,等.高低齿迷宫密封泄漏量实验及计算分析[J].工程热物理学报,2015,36(9):1889～1893.

[11] 曹丽华,胡鹏飞,徐伟,等.动静态汽封内部流场的数值模拟[J].化工机械,2010,37(5):617～621.

EffectofEccentricityandRotationalSpeedonDiaphragmSealLeakageofSteamTurbine

CAO Li-hua, LI Chao, LI Pan

(SchoolofEnergyandPowerEngineering,NortheastDianliUniversity,Jilin132012,China)

Through employing the RNGk-εturbulence model and basing on the finite volume method to resolve the 3D compressible Reynolds time-averaged N-S equations, the influence of both eccentric distance and rotational speed on the leakage of diaphragm seal was simulated. The results show that, under the same seal clearance and within a certain range of rotor eccentricity, the leakage flow becomes larger with the increase of the eccentricity; and when the leakage flow comes to the maximum value, it gradually decreases and tends to a stable value; when the rotor is at the eccentric and non-eccentric conditions, the diaphragm seal leakage flow within certain speeds reduces with increasing speed.

steam turbine, diaphragm seal, eccentricity, rotational speed, leakage flow

*国家自然科学基金项目(51476192，51576036)。

**曹丽华，女，1973年10月生，教授。吉林省吉林市，132012。

TQ051.6

A

0254-6094(2016)05-0645-04

2015-12-06)