异类传感器多目标检测跟踪与识别随机集模型
石绍应, 王小谟, 曹 晨, 张 靖, 汪先超
(1. 中国电子科学研究院, 北京 100041; 2. 空军预警学院, 湖北 武汉 430019)
异类传感器多目标检测跟踪与识别随机集模型
石绍应1,2, 王小谟1, 曹 晨1, 张 靖1, 汪先超2
(1. 中国电子科学研究院, 北京 100041; 2. 空军预警学院, 湖北 武汉 430019)
为在空中预警监视系统中实现多异类传感器多目标联合检测、跟踪与识别,在多目标检测、跟踪的随机有限集模型基础上,进行多异类传感器多目标联合检测、跟踪与识别的理论模型与处理框架研究。通过对目标的运动学状态与目标识别属性状态统一描述,把多目标状态建模为一个用随机有限集描述的全局状态。通过对运动学传感器与属性传感器模型分析,把各异类传感器建模为一个全局传感器,并把各传感器的测量建模为一个用随机有限集描述的全局测量。根据全局状态与全局测量模型,把异类传感器多目标联合检测、跟踪与识别过程描述为Bayes滤波过程,并给出了相应的多异类传感器多目标联合检测、跟踪与识别处理框架。通过仿真试验验证了理论模型与框架的有效性。
随机有限集; 多目标联合检测;跟踪与识别; 多异类传感器; 融合
0 引 言
对作用范围内的各类目标进行检测、跟踪和识别是空中预警监视系统的基本任务,一般由雷达、电子支援措施(electronic support measures, ESM)、通信支援措施、敌我识别/二次雷达、红外成像、合成口径雷达/逆合成口径雷达成像等众多不同传感器共同完成。但目前通常的处理过程是先由特定传感器对目标进行检测、跟踪,然后再由相应目标识别传感器进行目标身份属性的识别。这两个阶段一般是割裂开的,导致目标检测、跟踪无法利用目标识别信息,而目标识别也甚少利用目标检测、跟踪信息。
造成这种相对孤立、逐级进行处理的原因主要有两方面:一是来自不同传感器或信源的信息千差万别[1]。既有精确数据,也有不精确、不确定、不完全、模糊、随机乃至互相矛盾数据[2]。常用的专家系统理论方法,如模糊数学理论、Dempster-Shafer证据理论、Bayes理论等,没有一种理论能够处理全部类别的数据。二是多传感器多目标系统本身极其复杂。这些系统需要处理:随机变化的目标集,随机变化的传感器,由这些传感器产生的随机变化的观察/测量集。由此导致以上常用的专家系统理论无法统一进行多传感器多目标检测、跟踪、识别处理。
为提供统一的多传感器多目标融合处理理论基础,文献[1,3]基于随机集理论,提出了信息融合的有限集统计理论,希望以统一的理论框架,自顶向下系统解决多传感器多目标检测、跟踪、识别、态势评估、威胁估计,乃至传感器管理问题。基于有限集统计理论,文献[1]建立了多目标检测、跟踪的理论模型,并提出了概率密度假设(probability hypothesis density, PHD)滤波算法[4]、带有基分布的PHD(cardinalized PHD, CPHD)滤波算法[5]、多伯努利滤波器算法[6]等近似计算方法。在此基础上,文献[7-12]众多学者提出了多种扩展形式的PHD、CPHD与多伯努利滤波算法。目前,基于随机集[13-14]的这一理论在多传感器多目标检测与跟踪方面的研究比较深入、充分,取得了较大进展。但是在多传感器多目标识别方面,尤其是在多传感器多目标检测、跟踪、识别的统一处理方面的研究还不多。
本文在多目标检测、跟踪的随机有限集模型基础上,研究多异类传感器多目标联合检测、跟踪与识别模型,并构建多异类传感器多目标联合检测、跟踪、识别框架。通过仿真试验,验证了文中提出的理论模型与框架的有效性。
1 多目标检测、跟踪的随机有限集模型
1.1 单目标运动模型
设目标运动状态的向量表示为
x=(x,y,z,vx,vy,vz,ax,ay,az)
(1)
式中,x,y,z为目标在空间的位置;vx,vy,vz为目标速度;ax,ay,az为目标加速度。
目标的运动状态随时间变化过程可描述[1, 15]为
xk+1=Tk(xk,vk)
(2)
式中,xk+1表示在k+1时刻的目标状态;xk表示在k时刻的目标状态;vk为状态转移过程噪声,且假设vk是服从均值为0、协方差为Q的独立同分布高斯白噪声序列;Tk表示转换函数。
1.2 单目标测量模型
假设运动学传感器(例如雷达)的测量结果与目标状态之间为线性关系[1,16-21],则在k时刻传感器对于目标n的测量方程为
(3)

假设当前测量独立于之前的所有测量,则运动学传感器测量的似然函数可描述为
(4)
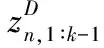
1.3 随机有限集框架下的多目标运动模型
设有N个目标,N可在0至某一最大数之间变化(实际中设备最大处理能力即为这一最大数),其中第n个目标运动状态根据式(1)描述为xn,则全部N个目标的状态用有限状态集[1]描述为
X={x1,x2,…,xN}
(5)
Ξk={xk,1,…,xk,N(k)}⊆X∈,N(k)=0,1,…,N
(6)
由文献[1-2,14]中随机有限集的定义可知,式中Ξk为定义于上的随机有限集。
根据式(6),设在k时刻多目标状态的随机有限集为Ξk,在该时刻具体的多目标状态实现为Xk,则在k+1时刻,总的多目标状态包含:在该时刻仍然存活的目标、由上一时刻目标派生的目标、自发出现的目标3部分。因此,在k+1时刻,多目标状态的随机有限集模型如下[1, 11]:
Ξk+1=Sk+1(Xk)∪Bk+1(Xk)∪Γk+1
(7)
式中,Sk+1(Xk)为在k+1时刻仍然存活的多目标的随机有限集;Bk+1(Xk)为由k时刻目标派生的多目标的随机有限集;Γk+1为在k+1时刻自发出现的多目标的随机有限集。
在k+1时刻的具体多目标状态Xk+1为该时刻多目标状态的随机有限集Ξk+1的具体实现。因此,类似与单目标状态的统计特性可用马尔可夫转移密度描述,多目标状态随机有限集Ξk+1的统计特性可用如下多目标状态转移密度函数描述[1,11]:
fk+1|k(Xk+1|Xk)
(8)
式(8)描述的多目标状态转移密度函数在应用中可根据具体情况,利用各类型目标各自的运动模型进行构造[1,22]。
1.4 随机有限集框架下的多目标测量模型
设在k时刻有Nk个目标,由一运动学传感器(如雷达)对这些目标进行测量,则k时刻测量结果可建模为该传感器的一个全局测量结果[1,22]:
(9)

考虑k时刻传感器存在虚警、漏警,则对该时刻Nk个目标的测量结果的随机集描述为
Σk=Dk(Xk)∪Uk(Xk)∪Ck
(10)
式中,Xk为k时刻全部目标集合;Dk(Xk)为k时刻全局传感器对目标进行了测量的测量结果随机有限集;Uk(Xk)为k时刻全局传感器对目标漏警的随机有限集;Ck为k时刻全局传感器虚警的随机有限集。
在k时刻的一次具体测量Zk为该时刻测量随机有限集Σk的一次具体实现。因此,随机有限集Σk的统计特性可用多传感器多目标似然函数进行描述[1,11]。
(11)
式(11)描述的多目标似然函数在应用中可根据具体情况,利用传感器测量模型进行构造[1,22]。
1.5 多目标检测与跟踪的Bayes滤波
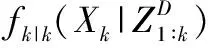
(1) 状态预测
(12)
(2) 状态更新
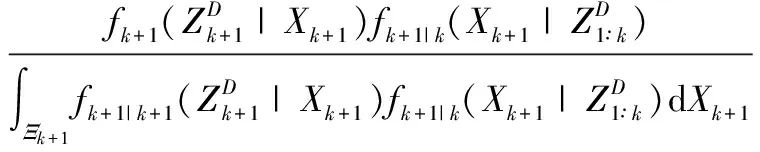
(13)
式(12)和式(13)中的积分为集积分。两式中的Ξk与Ξk+1分别为k时刻与k+1时刻多目标状态的随机有限集。
2 多异类传感器多目标联合检测、跟踪与识别模型
2.1 目标统一状态模型
目标的识别层次可分为:类型识别层次,如战斗机、轰炸机、运输机等;型号识别层次,如F-15、幻影2000等;敌我识别层次,如:友、中立、未知、敌。
不同类型飞机的几何外形、尺寸、飞行包线、机动能力都不同,尤其是机动能力。因此,基于飞机飞行包线与机动能力可识别目标的类型[16-20]。
在此,把与目标运动学特征相关的目标类型状态表示为静态的离散值[15]:
cT∈CT={cT,i∶i=1,2,…,NCT}
(14)
式中,NCT为目标类型数。
结合式(14)描述的目标类型,式(2)表示的目标运动学状态随时间变化过程[1,15]可进一步改写为
xk+1=Tk(xk,cT,i,vk)
(15)
为简单起见,式(15)用线性运动方程[11,16, 19-21]表示为
xk+1=Fxk+Guk+vk
(16)
式中,F为状态转移矩阵;G为增益矩阵;uk是与cT,i类目标机动能力对应的确定性控制输入。设cT,i类目标的飞行包线约束为Ei,则式(16)中xk+1,xk∈Ei。
k时刻的控制输入uk可建模为离散时间、有限状态的马尔可夫链[16,19,21],描述如下:
(17)
(18)
(19)
(20)
由于目标的类型不会随时间变化,由此目标运动状态与类型状态的统一马尔可夫转移密度可以表示为
p(xk+1,cT,i|xk,cT,i)=p(xk+1|xk,cT,i)
(21)
该转移密度取决于具体类型目标的运动模型[15-16,20]。
目标非类型属性是指与目标非运动学特征对应的其他属性,如目标的型号属性、敌我属性等。目标非运动学特征需要由专门的属性传感器测量。
目标的非运动学特征一般可分为静态特征与动态特征两类[20]。静态特征如目标的形状,不会随时间发生改变;动态特征如目标平台上各辐射源辐射情况会随时间发生变化(每个辐射源都存在开、关机两种状态,一些辐射源的频率还会发生改变)。此处主要讨论动态特征。
对于目标型号识别或者敌我识别等与目标非运动学特征对应的其他某一识别属性状态,也可表示为一个静态的离散值:
cA∈CA={cA,j∶j=1,2,…,NCA}
(22)
式中,NCA为目标这一识别属性数。根据其NCA个属性提取出MCA个特征,即特征矢量:
h=(h1,…,hMCA)
(23)
特征矢量的全体构成目标cA的特征空间HA,即
HA={h}
(24)
某一具体属性cA,j与其对应的特定特征值hj的先验概率密度可定义如下:
p(hj|cA,j)
(25)
因此,目标非类型属性及其动态特征的马尔可夫转移密度可以表示为
(26)
该转移密度及目标特征的先验概率密度决定于具体的目标特征提取过程与特征空间模型。
结合式(1)、式(14)和式(22),目标的统一状态可表示为
y=(x,cT,cA)
(27)
2.2 随机有限集框架下目标统一状态变化模型
把第1.3节中随机有限集框架下的多目标运动模型扩展为包含目标运动状态与识别属性状态的多目标统一状态变化模型。同样,设有N个目标,N可在0至某一最大数之间变化,根据式(27)描述的目标统一状态,其中第n个目标状态表示为
yn=(xn,cT,i,cA,j)
(28)
则全部N个目标的状态用有限状态集描述可由式(5)扩展为
Y={y1,y2,…,yN}
(29)
Ξk={yk,1,…,yk,Nk}⊆Y∈,Nk=0,…,N
(30)
同样,根据式(30),设在k时刻多目标状态的随机有限集为Ξk,在该时刻具体的多目标状态实现为Yk。则在k+1时刻总的多目标状态包含:在该时刻仍然存活的目标、由上一时刻目标派生的目标、自发出现的目标3部分。因此,在k+1时刻,多目标状态的随机有限集模型可由式(7)扩展为
Ξk+1=Sk+1(Yk)∪Bk+1(Yk)∪Γk+1
(31)
式中有关符号的意义与式(7)中的一样。
为此,描述多目标状态随机有限集Ξk+1统计特性的多目标状态转移密度函数可由式(8)扩展为
fk+1|k(Yk+1|Yk)
(32)
式(32)描述的多目标状态转移密度函数在应用中可根据具体情况,利用各类型目标各自的运动模型和目标属性状态转移模型进行构造。
2.3 随机有限集框架下异类传感器统一测量模型
与运动学传感器测量类似,假设某个非类型属性传感器(例如ESM)的测量结果与目标状态之间为线性关系,则在k时刻传感器对于属性为cA,i的目标n的测量方程为
(33)

属性传感器测量的似然函数可描述如下:
(34)

不失一般性,设在k时刻有Nk个目标,由一个运动学传感器与一个非类型属性传感器对这些目标进行测量,则k时刻两个传感器的测量结果可建模为全局传感器的一个全局测量结果[1,22]:
(35)

为简化全局测量模型,考虑到运动学传感器与属性传感器为异类传感器,可在每一时刻对各传感器测量结果预先进行处理,对某一目标n在k时刻形成如下的全局测量向量:
(36)
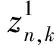
Zk={z1,k,…,zn(k),k}
(37)
式中,nk为预处理后的测量总数,一般nk≥max(nD,k,nA,k)。
考虑k时刻全局传感器存在虚警、漏警,则对该时刻Nk个目标测量结果的随机集描述可由式(10)扩展为
Σk=Dk(Yk)∪Uk(Yk)∪Ck
(38)
式中,Yk为k时刻全部目标集合,其他符号的意义与式(10)一样。因此,描述随机有限集Σk统计特性的多传感器多目标似然函数可由式(11)扩展为
fk(Zk|Yk)
(39)
式(39)描述的多传感器多目标似然函数在应用中可根据具体情况,利用各传感器各自的测量模型进行构造。
2.4 多传感器多目标检测、跟踪、识别的Bayes滤波
把第1.5节多目标检测与跟踪Bayes滤波扩展为多传感器多目标检测、跟踪、识别的Bayes滤波。
设fk|k(Yk|Z1∶k)表示多目标后验密度函数,其中Yk表示k时刻多目标状态,Z1∶k表示1~k时刻全局传感器的测量结果。根据式(32)和式(39),多传感器多目标检测、跟踪、识别的Bayes滤波同样可描述如下:
(1) 状态预测
fk+1|k(Yk+1|Z1∶k)=
∫Ξkfk+1|k(Yk+1|Yk)fk|k(Yk|Z1∶k)dYk
(40)
(2) 状态更新
fk+1|k+1(Yk+1|Z1∶k+1)=
(41)
式(40)和式(41)中的积分为集积分,两式中的Ξk和Ξk+1分别为k时刻和k+1时刻多目标状态的随机有限集。
需要注意的是,由式(40)和式(41)描述的多传感器多目标Bayes滤波过程在实现时计算难度大。在实际应用中可基于有限集统计理论,采用PHD滤波算法、CPHD滤波算法、多伯努利滤波算法等近似算法进行计算实现。
3 多异类传感器多目标检测、跟踪、识别处理框架
根据第2节基于随机有限集的多异类传感器多目标检测、跟踪与识别模型,构建如图1所示的多异类传感器融合的多目标检测、跟踪、识别框架。
图1中,运动学传感器(如雷达)负责对多目标运动学状态的测量。假设目标有M种不同的非类型属性(由运动学特征描述的类型属性除外),非类型属性测量传感器1~M表示M种不同的传感器,分别负责对其中的一种非类型属性进行测量。
(M+1)个异类传感器在k时刻的测量结果输出给测量数据预处理模块进行预先处理,形成如式(36)、式(37)所描述的k时刻的全局测量。该处理框架中的预处理模块主要解决多异类传感器测量数据关联问题。在具体应用中的数据关联算法应根据各传感器实际情况选取,例如雷达与ESM数据关联可采用基于模糊综合分析理论的关联算法。

图1 多异类传感器融合多目标处理框架Fig.1 Processing framework of multiple dissimilar sensors multi-target
假设目标可分为NCT种类型,对每一种类型cT∈CT={cT,i:i=1,2,…,NCT}目标的运动学特性,设计一个对应的检测、跟踪与识别处理滤波器。每种类型滤波器均在上一时刻(即k-1时刻)处理结果的基础上,对测量数据预处理模块输出的k时刻全局测量进行处理,得到该种类型滤波器在k时刻的包含多目标运动状态、非类型属性的处理结果。
多目标航迹综合模块负责对NCT种类型滤波器的处理结果进行综合处理,形成统一的多目标处理结果,该处理结果包括每个目标的运动状态、类型属性、其他非类型属性。因此,基于随机有限集的多异类传感器融合的多目标处理框架实现了对多目标的检测、跟踪与识别。
4 仿真验证
4.1 仿真试验简介
试验根据第3节基于随机有限集的多异类传感器多目标检测、跟踪与识别模型,以及图1所示的多异类传感器多目标检测、跟踪、识别框架,采用作者在文献[23]中提出的具体处理方法—基于跳转马尔可夫系统模型高斯混合概率假设密度滤波算法(jump markov system model gaussian mixture probability hypothesis density filtering, JMS-GMPHDF)的雷达、ESM综合多目标检测、跟踪与识别方法。综合雷达和ESM两种异类传感器的量测结果,进行多目标检测、跟踪与识别。试验中,雷达量测结果用于目标的类型识别[24-25](如战斗机、运输机等类型),ESM量测结果用于目标的型号识别(如F-15、幻影2000等型号)。
4.2 试验条件设置
仿真活动场景为(-50, 50)×(-50, 50)(单位:km)。假设目标包含两种类型:C1(战斗机)、C2(运输机)。两类目标的速度模型如表1所示。

表1 两类目标速度模型
两类目标的加速度模型如下:
运输机(单位:m/s2):
(1) ax=0, ay=0 (2) ax=10, ay=10
(3) ax=10, ay=-10 (4) ax=-10, ay=10;
(5) ax=-10, ay=-10
(42)
战斗机(单位:m/s2):
(1) ax=0, ay=0 (2) ax=50, ay=50
(3) ax=50, ay=-50 (4) ax=-50, ay=50
(5) ax=-50, ay=-50
(43)
假设目标辐射源特性与目标身份属性关系如表2所示。

表2 目标辐射源特性与身份属性
辐射源E1,1~E1,20表示机载火控雷达,E2,1~E2,20表示多功能攻击雷达,E3,1~E3,10表示机载预警雷达,E4,1~E4,10表示导航雷达,E5,1~E5,10表示二次雷达/敌我识别(发射询问、应答信号)。
4.3 仿真数据
仿真生成4批目标,采样80次,即滤波迭代时刻k=1,2,…,80,采样周期为T=3 s。
目标 1 类型为运输机C2,型号为TP10(预警机1),其身份属性为(C2,TP10),目标存活时刻为k=1,2,…,20。目标初始运动状态为x0=(0,100,0,-110),在k=10,11,12,13时刻目标的加速度模型为2,其他时刻的加速度模型为1。在k=10,11,12,13时刻目标辐射源{E3,1,E5,1}开机,在k=14,15,…,20时刻目标辐射源{E5,1}开机,其他时刻所有辐射源关闭。
目标 2 类型为运输机C2,型号为TP11(预警机2),其身份属性为(C2,TP11),目标存活时刻为k=18,19,…,40。目标初始运动状态为x0=(0,50,0,-160),在k=25、26时刻目标的加速度模型为4,其他时刻的加速度模型为1。在k=25、26时刻目标辐射源{E3,2,E5,1}开机,在其他时刻目标辐射源{E3,2}开机。
目标 3 类型为战斗机C1,型号为TP1(战斗机1),其身份属性为(C1,TP1),目标存活时刻为k=30,31,…,50。目标初始运动状态为x0=(-5 000, 200, 5 000, 300),在k=37,38,39时刻目标的加速度模型为4,在k=43,44,45时刻目标的加速度模型为3,其他时刻的加速度模型为1。在k=37,38,39时刻目标辐射源{E5,1}开机,在k=40,41,42时刻目标辐射源{E1,1}开机,在k=43,44,45时刻目标辐射源{E1,1,E5,1}开机,其他时刻所有辐射源关闭。
目标 4 类型为战斗机C1,型号为TP2(战斗机2),其身份属性为(C1,TP2),目标存活时刻为k=45,46,…,78。目标初始运动状态为x0=(-5 000, 320, 5 000, 230),在k=53,54,55时刻目标的加速度模型为3,在k=60,61,…,62时刻目标的加速度模型为4,在k=68,…,72时刻目标的加速度模型为4,其他时刻的加速度模型为1。在k=56,…,59时刻目标辐射源{E5,1}开机,在k=60,61,62时刻目标辐射源{E1,2}开机,在k=63,64,…,67时刻目标辐射源{E5,1}开机,其他时刻所有辐射源关闭。
仿真的目标原始航迹如图2所示。仿真的雷达测量数据如图3所示。

图2 目标原始航迹Fig.2 Original tracks of targets
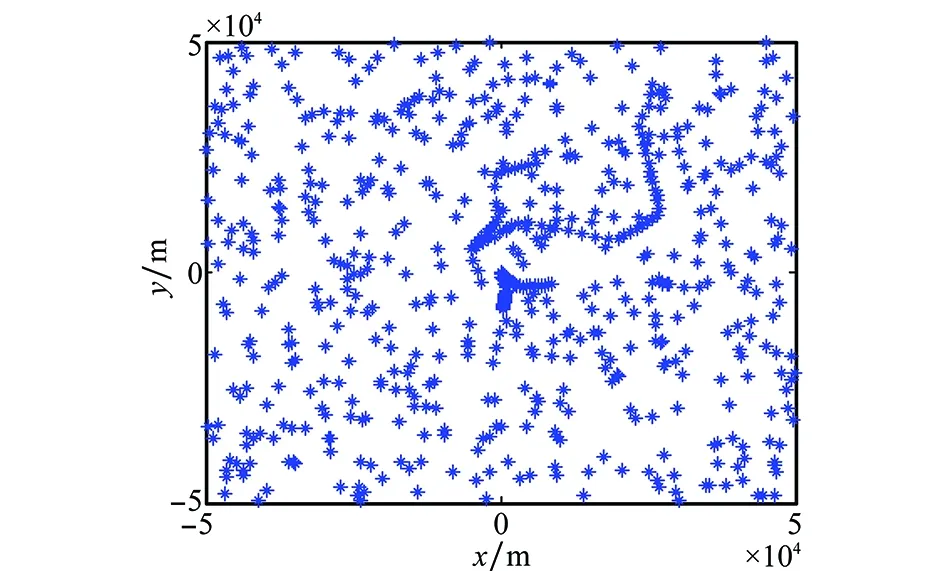
图3 仿真生成的雷达测量数据Fig.3 Simulated radar measurement data
4.4 处理结果
多目标检测、跟踪、识别的结果如图4所示,实际处理时,当航迹中的点迹数大于等于2点时才显示最后一点。从图中看见:目标1的航迹编号为T01,在检测到第3点时就被识别为第1类,即运输机。在检测到辐射源{E3,1}以后,即被识别为预警机1;目标2的航迹编号为T03,在检测到第3点时就被识别为第1类,即运输机,因也已检测到辐射源{E3,2},以后被识别为预警机2;目标3的航迹编号为T04,检测到第3点时被识别为第1类,即运输机,在检测到第4点后被识别为第2类即战斗机。在检测到辐射源{E1,1}以后,被识别为战斗机1;目标4的航迹编号为T05,检测到前3点时被识别为第1类,即运输机,在检测到第4点后被识别为第2类即战斗机。在检测到辐射源{E1,2}以后,被识别为战斗机2。
全部时刻的目标数估计情况如图5所示。

图4 多目标检测、跟踪与识别的结果Fig.4 Result of multi-target detection, tracking and recognition
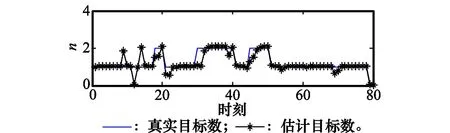
图5 各时刻目标数估计情况Fig.5 Estimated targets number in each times
50次试验的平均多目标估计误差用最优子模型分配距离[26]进行描述。试验时设置最优子模型分配距离阶数p=1,截取参数c=200。结果如图6所示。
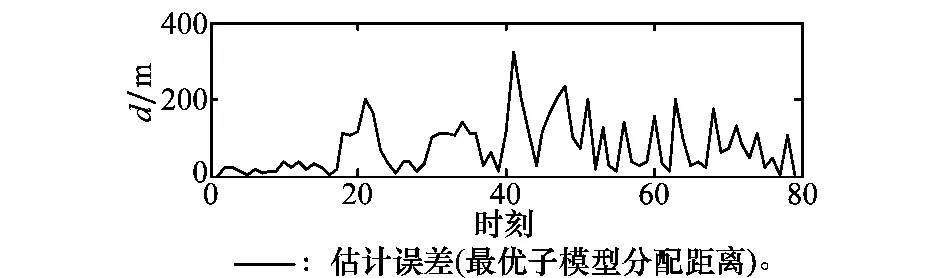
图6 50次试验平均多目标估计误差Fig.6 Estimated multi-target average status error with 50 times
5 结 论
基于随机集及有限集统计理论,首先,把单目标的运动学状态与非运动学属性状态表示为一个整体状态,并把多目标的整体状态建模为一个用随机有限集描述的全局状态;其次,把运动学传感器与各种属性传感器建模为一个全局传感器,把各传感器的测量建模为一个全局传感器测量;最后,在前两部分模型基础上,得以给出异类传感器多目标检测、跟踪、识别的Bayes滤波过程描述,并给出了相应的异类传感器融合多目标识别结构框图。
经过仿真试验验证,本文提出的异类传感器多目标检测、跟踪、识别的随机有限集模型是可实现的、有效的。
[1] Mahler R.Statisticalmultisourcemultitargetinformationfusion[M]. Boston: Artech House, 2007.
[2] Jousselme A L, Bosse E. Fusion of imperfect information in the unified framework of random sets theory: application to target identification[R]. Defence R&D Canada-Valcartier, 2007.
[3] Mahler R. Nonadditive probability, finite-set statistics, and information fusion[C]∥Proc.ofthe34thConferenceonDecision&Control, 1995: 1947-1952.
[4] Mahler R. A theoretical foundation for the Stein-Winter probability hypothesis density (PHD) multitarget tracking approach[C]∥Proc.oftheMSSSensorandDataFusion, 2000:1532-1541.
[5] Mahler R. A theory of PHD filters of higher order in target number[C]∥Proc.oftheSPIESignalProcessing,SensorFusion,andTargetRecognitionXV, 2006:753-761.
[6] Mahler R. Multitarget motion models[C]∥Proc.oftheSignalProcessing,SensorFusion,andTargetRecognitionVIII, 1999:58-67.
[7] Mahler R. Approximate multisensor CPHD and PHD filters[C]∥Proc.oftheConferenceonInformationFusion, 2010: 1-8.
[8] Punithakumar K, Kirubarajan T, Sinha A. Multiple-model probability hypothesis density filter for tracking maneuvering targets[J].IEEETrans.onAerospaceandElectronicSystems, 2008, 44(1): 87-98.
[9] Georgescu R, Willett P. The multiple model CPHD tracker[J].IEEETrans.onSignalProcessing, 2012, 60(4): 1741-1751.
[10] Vo B T, See C M, Ma N, et al. Multi-sensor joint detection and tracking with the Bernoulli filter[J].IEEETrans.onAerospaceandElectronicSystems, 2012, 48(2): 1385-1402.
[11] Vo B N, Ma W K. Joint detection and tracking of multiple maneuvering targets in clutter using random finite sets[C]∥Proc.oftheControl,Automation,RoboticsandVisionConference, 2004, 2:1485-1490.
[12] Vo B N, Singh S, Doucet A. Sequential Monte Carlo methods for multi-target filtering with random finite sets[J].IEEETrans.onAerospaceandElectronicSystems, 2005, 22(4): 1224-1245.
[13] Nguyen H T.Anintroductiontorandomsets[M]. New York: Chapman & Hall/CRC, 2006.
[14] Molchanov I.Theoryofrandomsets[M]. New York: Springer-Verlag, 2005.
[15] Ristic B, Gordon N, Bessell A. On target classification using kinematic data[J].ElsevierInformationFusion, 2004, 5(1): 15-21.
[16] Challa S, Pulford G W. Joint target tracking and classification using radar and ESM sensors[J].IEEETrans.onAerospaceandElectronicSystems, 2001, 37(3): 1039-1055.
[17] Angelova D, Mihaylova L. Joint target tracking and classification with particle filtering and mixture Kalman filtering using kinematic radar information[J].ElsevierDigitalSignalProcessing, 2006, 16(1): 180-204.
[18] Yang W, Fu Y W, Long J Q, et al. Joint detection, tracking, and classification of multiple targets in clutter using the PHD filter[J].IEEETrans.onAerospaceandElectronicSystems, 2012, 48(4): 3594-3609.
[19] Farina A, Lombardo P, Marsella M. Joint tracking and identification algorithms for multisensor data[J].IEEProceedings-RadarSonarandNavigation, 2002, 149(6): 271-280.
[20] Mei W, Shan G, Li X R. Simultaneous tracking and classification a modularized scheme[J].IEEETrans.onAerospaceandElectronicSystems, 2007, 43(2): 581-599.
[21] Li X R, Jilkov V. Survey of maneuvering target tracking part I: dynamic models[J].IEEETrans.onAES, 2003, 39(4): 1333-1364.
[22] Hall D L, Llinas J.Handbookofmultisensordatafusion[M]. New York: Chemical Rubber Company Press, 2001.
[23] Shi S Y, Du P F, Zhang J, et al. Multi-target detection, tracking and recognition using radar and ESM sensors[J].SystemsEngineeringandElectronics,2016,38(7):1524-1531.(石绍应, 杜鹏飞,张靖,等.雷达与ESM综合多目标检测、跟踪与识别[J].系统工程与电子技术, 2016,38(7):1524-1531.)
[24] Wang F Y, Luo D, Liu H W. Low-resolution airborne radar aircraft target classification[J].JournalofRadars, 2014, 3(4): 444-449. (王福友, 罗钉, 刘宏伟. 低分辨机载雷达飞机目标分类识别技术研究[J]. 雷达学报, 2014, 3(4):444-449.)
[25] Wu J, Zhou G J J, Zhu J H. Radar target recognition method under noise background[J].SystemsEngineeringandElectronics, 2010, 32(7): 1403-1407. (吴杰, 周建江, 朱劼昊. 一种噪声背景下的雷达目标识别方法[J]. 系统工程与电子技术, 2010, 32(7): 1403-1407.)
[26] David L H, James L.Handbookofmultisensordatafusion[M]. 2nd ed. New York: CRC Press, 2008.
Random set models of dissimilar sensors for multi-target detection, tracking and recognition
SHI Shao-ying1,2, WANG Xiao-mo1, CAO Chen1, ZHANG Jing1, WANG Xian-chao2
(1.ChinaAcademyofElectronicsandInformationTechnology,Beijing100041,China;2.AirForceEarlyWarningAcademy,Wuhan430019,China)
In order to detect, track, and recognize multi-target jointly by fusion multiple dissimilar sensors in the airborne warning system, the theoretical models and processing framework for multi-target joint detection, tracking and recognition of dissimilar sensors are studied based on the random finite set theory. By describing the single target’s kinematics states and recognition attribute states unifiedly, the multi-target states are modeled as a global state that is described by the random finite set. By analyzing the models of a kinematic sensor and an attribute sensor, the dissimilar sensors are modeled as a global sensor, and the measurements of those dissimilar sensors are modeled as a global measurement. Based on the models of global state and global measurement, the process of multi-target detection, tracking and recognition of dissimilar sensors are described by Bayes filtering, and the structure of multi-target recognition of dissimilar sensors fusion is established. Simulation results suggest that the proposed models and processing framework are executable and effective.
random finite set; multi-target joint detection; tracking and recognition; multiple dissimilar sensors; fusion
2016-04-07;
2016-05-26;网络优先出版日期:2016-09-30。
总装预研项目(51307020103)资助课题
TP 391, TN 911.7
A
10.3969/j.issn.1001-506X.2016.12.01
石绍应(1975-),男,副教授,博士研究生,主要研究方向为通信与信息系统。
E-mail:shisy2006@163.com
王小谟(1938-),男,中国工程院院士,博士研究生导师,主要研究方向为雷达系统、信息系统。
E-mail:wangxiaomo_caeit@163.com
曹 晨(1974-),男,研究员,博士研究生导师,主要研究方向为雷达系统。
E-mail:caochen998@sina.com
张 靖(1975-),女,高级工程师,博士,主要研究方向为多源信息融合、信息处理。
E-mail:prettypic126@126.com
网络优先出版地址:http:∥www.cnki.net/kcms/detail/11.2422.TN.20160930.1142.014.html

