直线运动滚动导轨副的法向接触力学模型

田红亮,郑金华,陈甜敏,余媛,张屹

(三峡大学机械与动力学院,443002,湖北宜昌)



直线运动滚动导轨副的法向接触力学模型

田红亮,郑金华,陈甜敏,余媛,张屹

(三峡大学机械与动力学院,443002,湖北宜昌)

借助赫兹点接触形成椭圆接触区域的计算机制,考虑外加法向工作总载荷和法向预紧力,构建了直线运动滚动导轨副的运动结合部法向接触力学模型;采用第一类与第二类完全椭圆积分解算了椭圆离心率。给出一个滚珠斜向下压缩力与外加法向工作总载荷的隐函数方程,并重点推出了单个滚珠法向压缩量、滚珠法向接触刚度、滑块总压缩量、滑块整体法向接触刚度的解析解。数值仿真结果表明:单个滚珠的压缩量随着沟道曲率半径系数的增加而增加;滚珠的法向接触刚度随着单个滚珠压缩量的增大而向上凸弧式增大,但随着沟道曲率半径系数的增大而减小;滑块的总压缩量随着外加法向工作总载荷或沟道曲率半径系数的增大而增大,但随着预紧力、每列滚珠总数或接触角的增加而减小;当外加法向工作总载荷远远小于最大外加法向工作总载荷时,可视滑块整体法向接触刚度为常值;当外加法向工作总载荷接近最大外加法向工作总载荷时,外加法向工作总载荷对滑块整体法向接触刚度有显著影响,滑块整体法向接触刚度随着外加法向工作总载荷的增加而迅速减小;滑块整体法向接触刚度随着预紧力、每列滚珠总数或接触角的增加而提升,但随着外加法向工作总载荷或沟道曲率半径系数的增加而减小。结合部法向接触力学模型的建立将有助于分析直线运动滚动导轨副运动接触表面间的实际接触状态。

数控机床;滚动导轨副;滚珠;滑块;轨道;法向工作载荷;法向预紧力

结合部的接触刚度对机械及机械结构的静、动态特性具有重要影响[1]。从运动角度来看,结合部可分为固定结合部和运动结合部。在数控机床整机性能研究中,目前对固定结合部的建模方法和建模精度已经取得了比较成熟的理论依据与应用结果,但对运动结合部的建模方法研究还比较有限。

导向支承部件的作用是支承和限制运动部件按规定的方向运动,这样的部件通常称为导轨副。直线运动滚动导轨副的结构主要由轨道、滑块、滚珠和端盖组成,其中滚珠与滑块、轨道的沟槽同时接触。如今,分析直线运动滚动导轨副运动结合部的法向接触力学行为主要采用试验与解析2种主流研究方法。

(1)辨识直线运动滚动导轨副运动结合部法向接触力学行为的试验方法。米良等进行了导轨模态试验,采用多输入、单输出的方式,试验时将导轨固定于试验台上,分别测出各点的传递函数后,借用特征系统实现算法获得了该导轨各阶固有频率、阻尼比以及相应的振型[2-3]。李磊等用大直径螺栓将直线滚动导轨副固定于地面进行约束状态下的模态试验,采用力锤对滑块进行激振,使用三向加速度传感器获取加速度信息,通过频谱分析并结合振型分析得到其传递函数,揭示了预紧力和外部激励等因素对直线滚动导轨副动态特性的影响[4]。尹宜勇等在直线导轨的工作台上安装激光位移传感器,检测了双丝杠与直线导轨结合部z轴方向的位移[5]。朱坚民等在试验中使用了BK 8208型激振力锤、4个BK 4525B型三向加速度传感器以及搭载了NI PXIe-4498动态信号采集模块的NI PXIe-1075数据采集系统,使用ModalView模态分析软件进行试验数据的采集和处理,采用单点激振多点拾振的锤击法对滚珠丝杠进给系统进行模态测试,获得了前6阶固有频率和模态振型[6]。Hung基于赫兹接触理论建立了不同载荷作用下的滚动导轨副有限元模型,研究了外载荷对导轨副刚度的影响,并通过试验对有限元模型进行了修正[7]。以上文献中辨识直线运动滚动导轨副运动结合部法向接触力学行为的试验方法具有3个共同缺陷:①试验方法均需要实测频率响应函数,但由于测量部位处于结合部处,实际测量比较困难,故试验设计的难度很高;②试验值通常很小,很容易受到噪声的干扰;③基础试验数据有限,没有形成公共的数据库,数据只保存于部分研究机构,并且其适用范围还有待于进一步验证。目前,工程上还没有一个标准的直线运动滚动导轨副用来检验基础数据的有效性。

(2)辨识直线运动滚动导轨副运动结合部法向接触力学行为的解析方法。Ohta等考虑接触角和预紧力推导了直线导轨型再循环直线滚珠轴承的法向刚度[8]。Dhupia等给出了嵌在2个沟槽里的单个滚珠的接触变形量[9]。蒋书运等以带滚珠丝杠副直线导轨的结合部为研究对象,借助于弹性力学中的赫兹接触理论,分析计算了直线滚动导轨的线刚度、滚珠丝杠副和角接触滚动轴承的轴向刚度,建立了带滚珠丝杠副的机床直线导轨结合部的动力学模型[10-11]。方兵等采用矩阵变换分析方法,建立了双列角接触球轴承的接触变形关系[12]。刘耀等建立了直线滚珠导轨的圆柱面-球面结合部数学模型,用解析方法求解外载荷作用时的结合部变形,研究了不同外载荷作用下直线滚珠导轨圆柱面-球面结合部的静特性[13]。刘静等通过Matlab编程计算,建立了滚子与外圈滚道接触变形的拟合表达式[14]。胡建忠等综合考虑滚珠、螺母和丝杠滚道的几何参数,建立了滚珠丝杠副接触角模型[15]。卢宪玖等考虑角接触球轴承的几项重要基本参数(密合度、钢球数目等)及接触角随轴向载荷的变化,建立了角接触球轴承的几何和数学模型[16]。王燕霜等给出了特大型双排四点接触球轴承的一种静承载曲线的设计方法,分析了轴承结构参数对此类轴承承载能力的影响[17]。杨家军等依据赫兹弹性接触理论,以滚柱为研究对象,对3种变形分别进行了理论分析和计算[18]。卓耀彬等考虑滚珠陀螺力矩和离心力的影响,分析了高速滚珠关节轴承的整体受力平衡、结构尺寸关系、接触点的综合曲率、接触角的变化、弹性变形关系、滚珠的自转和公转、滚珠受力平衡等因素,建立了滚珠关节轴承在联合载荷及高速旋转工况下的动力学平衡方程[19-20]。上述文献中,辨识直线运动滚动导轨副运动结合部法向接触力学行为的解析方法具有2个共同的缺点:①没有严格区分直线运动滚动导轨副所承受的外加法向工作载荷与法向预紧力的区别,没有对影响直线运动滚动导轨副动态特性的各种因素进行深入研究,在建模过程中做了大量简化,并忽略了一些结合部属性,因此所建立的解析模型通用性不强;②所给出的嵌在2个沟槽里单个滚珠的接触变形量数学公式常常包括许多经验常数,而这些经验常数往往缺少特定的物理含义,可移植性差,此外,这些接触变形量公式涉及三维空间内滚动导轨的赫兹点接触,赫兹接触区域是一个椭圆,椭圆离心率未知,因而不便应用。椭圆离心率等赫兹系列参数的理论确定是一个不可回避的重要问题。

迄今为止,国内外众多的研究者已经进行了大量的直线运动滚动导轨副结合部特性的试验研究,积累了较为丰富的试验数据。但是,试验数据毕竟是有限的,所以还需要发展理论解析算法。通过机理研究创建直线运动滚动导轨副结合部的本构模型,揭示其内在的本质规律,从而使得所建模型具有通用性,仍是研究者所追求的理想目标。本文根据赫兹点接触形成椭圆接触区域的计算原理,通过反演获得了椭圆离心率e,重点推出了单个滚珠法向压缩量δ、滚珠法向接触刚度keq、滑块总压缩量z和滑块整体法向接触刚度kc的法向接触力学方程,分析了外加法向工作总载荷F、法向预紧力F0、每列通道的工作滚珠总数N、接触角α和沟道曲率半径系数f对直线运动滚动导轨副运动结合部法向接触力学行为(包括单个滚珠法向压缩量、滚珠法向接触刚度、滑块总压缩量、滑块整体法向接触刚度)的影响性质、影响程度及影响规律。

1 滚珠与滑块和轨道的法向接触

在直线运动滚动导轨副中,滚珠位于滑块和轨道之间,滚珠与滑块的沟槽圆弧、轨道的沟槽圆弧紧密接触。单个滚珠与滑块和轨道的接触情况见图1,其中Oc为滑块的沟槽圆弧圆心,Or为轨道的沟槽圆弧圆心,Ob为滚珠的圆心,R为滑块或轨道的沟槽圆弧半径,rb为滚珠半径,Q为单个滚珠所受的局部外加法向工作载荷,α为接触角(滚道型面与滚珠接触点的法线NM与丝杠轴向的垂线间的夹角)。单圆弧型面的滚道沟槽圆弧半径R稍大于滚珠半径rb。

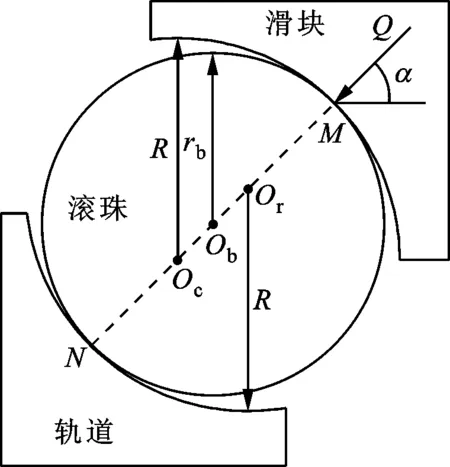
图1 单个滚珠与单圆弧型面滑块和轨道的接触

单个滚珠沿法线NM方向的压缩量[21]为

(1)

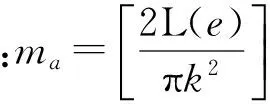
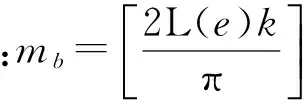
由式(1)得

(2)

式(2)可写为

(3)

式中:H称为类接触刚度(单位是N·m-3/2),不同于通常意义上的接触刚度(单位是N·m-1),并且

根据式(3),可得单个滚珠与滑块和轨道同时接触时滚珠的法向接触刚度

(4)

因为H是常数,故由式(4)可见,滚珠的法向接触刚度只由滚珠的法向压缩量决定。直线运动滚动导轨副在数控机床运转时,滚珠所受局部外加法向工作载荷时刻在改变,依据式(3),会引起滚珠的法向压缩量不断变化,再依据式(4),滚珠的法向接触刚度是变量,所以式(4)能够表达直线运动滚动导轨副具有变法向接触刚度的非线性特点。

2 直线运动滚动导轨副的法向接触

如果直线运动滚动导轨副总共有4列通道沟槽,在每列通道沟槽中参与接触的工作滚珠总数都为N,则直线运动滚动导轨副的滑块在法向横截面上的整体受力接触情形如图2所示,其中O1与O2分别为滑块与轨道的静平衡位置,z1与z2分别为滑块与轨道向下的压缩量,F为滑块受到的外加法向工作总载荷,F1～F4分别为4列通道沟槽中的滚珠1～4对滑块的支反力。

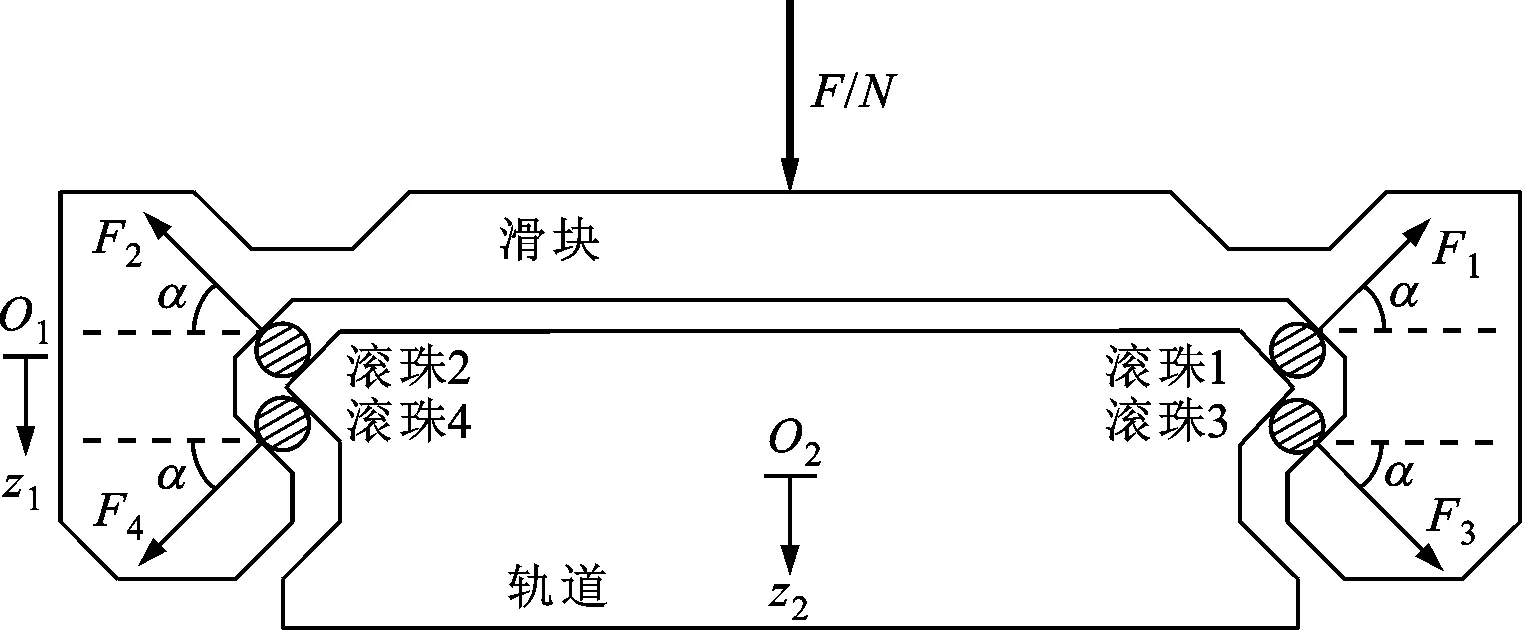
图2 滑块在法向横截面上的受力状态

假设4列滚珠在外加法向工作总载荷作用下一直保持压缩情形,滑块在法向上的静平衡条件为

(5)

由式(5)得

(6)

滑块沿水平方向上的静力学平衡原理为

(7)

由式(7)得

(8)

根据图2的左右结构对称性和式(8),可假定

(9)

F3=F4=FL

(10)

式中:Fu为轨道上面单个滚珠对滑块的支反力;FL为轨道下面单个滚珠对滑块的支反力。

由式(9)可知,轨道上面第1、2列滚珠的受力情况一样;由式(10)可知,轨道下面第3、4列滚珠的受力情况也一样。将式(9)和式(10)代入式(6)得

F+2NFLsinα=2NFusinα

(11)

滑块相对于轨道沿外加法向工作总载荷F方向的总压缩量(即导轨副发生的相对弹性变形量[22])为

z=z1-z2

(12)

根据图2,滑块对轨道上面任意一个滚珠的斜向下压缩力都为Fu,仿照式(3)得

(13)

类似地,根据图2,滑块对轨道下面任意一个滚珠的斜向上压缩力皆为FL,仿照式(3)得

(14)

直线运动滚动导轨副在安装过程中需施加法向预紧力,以增加接触面积,提高接触刚度。法向预紧力一般等于运动件及其上的工件等的重量。同样仿照式(3),可得法向预紧力

(15)

式中:δ0为单个滚珠的初始压缩量。

滚珠1和滚珠4在受法向预紧力之前和之后,以及在受外加法向工作载荷之后的变形协调状况如图3所示,其中δ1、δ4分别为滚珠1及滚珠4的轴向变化量。

图3 滚珠1与滚珠4的变形协调情形

滚珠1的轴向变化量

(16)

滚珠4的轴向变化量

(17)

根据连接的变形协调条件得

(18)

将式(16)与式(17)代入式(18)得

(19)

在图3中,滑块相对于轨道沿外加法向工作总载荷F方向的总压缩量

(20)

将式(19)代入式(20)得

(21)

由式(19)得

(22)

由式(13)得

(23)

由式(15)得

(24)

由式(14)得

(25)

将式(23)～(25)代入式(22)得

(26)

由式(11)得

(27)

将式(27)代入式(26)得

(28)

由式(28)可见:滑块对轨道上面的任意一个滚珠的斜向下压缩力Fu(因变量)是滑块所受到的外加法向工作总载荷F(自变量)的隐函数,且不能将此隐函数式(28)化成显函数。可将具体隐函数式(28)改写成更一般化的形式

(29)

将式(23)及式(24)代入式(21)得

(30)

将式(29)代入式(30)得

(31)

同样,由式(31)可见:滑块相对于轨道沿外加法向工作总载荷F方向的总压缩量z(因变量)是滑块所受到的外加法向工作总载荷F(自变量)的隐函数,也不能将此更加复杂的隐函数(式(31)中未出现自变量F)变成显函数。

参考式(29),将式(28)两边分别对F求一阶导数,得

(32)

由式(32)得

(33)

将式(31)两边分别对F求一阶导数得

(34)

式(34)可改写为

(35)

将式(33)代入式(35)得

(36)

如果函数z=z(F)在有限闭区间[0,Fmax]内单调、可导且dz/dF≠0,其中Fmax为滑块所受到的最大外加法向工作总载荷,则函数z=z(F)的反函数F=F(z)在有限闭区间[0,zmax]内也可导,其中zmax为滑块相对于轨道沿外加法向工作总载荷F方向的最大总压缩量,则直线运动滚动导轨副滑块的整体法向接触刚度

(37)

根据式(37)与式(29)可知:直线运动滚动导轨副滑块的整体法向接触刚度随着滑块所受到的外加法向工作总载荷的变化而变化。

由式(11)得

(38)

将式(38)代入式(26)得

(39)

且由式(38)得

Fu≥FL≥0

(40)

分析式(27)和图2,当滚珠进入承载区后,滑块所受到的外加法向工作总载荷F即由0逐渐增加到Fmax,轨道下面单个滚珠对滑块的支反力FL连续减小。一种极限情况是下半部滚珠(即第3、4列滚珠)全部不受载,此种情况在式(40)中对应的条件为

FL=0

(41)

将式(41)代入式(39)可解得F,即为滑块所受到的最大外加法向工作总载荷

(42)

为确定椭圆离心率e、类接触刚度H等系列参数,下面将给出一些辅助表达式。

图1中,单圆弧型面的滚道沟槽圆弧半径

R=fDb=2frb

(43)

式中:f为沟道曲率半径系数;Db为滚珠直径。

主曲率差

(44)

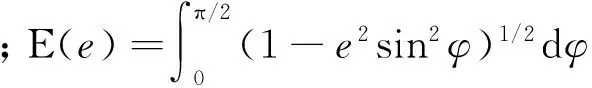
主曲率和

(45)

式中:ρij为物体i在接触点一对主平面j的主曲率。主曲率有正负号:对于凸面,即曲面与曲率中心在切线同一侧或曲率中心在物体之内,主曲率取正号;反之,对于凹面,即曲面与曲率中心在切线不同侧或曲率中心在物体之外,主曲率取负号。

主曲率差还可写为

(46)

可见,主曲率差F(ρ)是无量纲的,不同于文献[20]中主曲率差F(ρ)的单位——mm-1。

图1中,滚珠曲率中心在滚珠之内,主曲率取正号,滚珠的2个主曲率分别为

(47)

滚道的一个接触是平面接触,曲率半径近似无穷大;另一个接触的曲率中心在滚道之外,主曲率取负号。由式(43),滚道的2个主曲率[23]分别为

(48)

(49)

将式(47)～(49)代入式(46)得

(50)

式(1)中的一个局部系数为

(51)

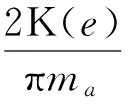
3 直线运动滚动导轨副的数值算例

日本精工株式会社NSK轴承公司的NSK LH45导轨副的滑枕宽度为120 mm,滑枕长度为139 mm,有1个滑块。其主要技术参数如下:滚珠材料为淬硬中碳调质钢40Cr;滚珠的弹性模量E1=206 GPa;滚珠的泊松比μ1=0.3;滚道材料为高碳铬轴承钢GCr15;滚道的弹性模量E2=206 GPa;滚道的泊松比μ2=0.3;滚珠半径rb=3.968 5 mm;沟道曲率半径系数f=0.52;1级法向预紧力为635 N;2级法向预紧力为1 042 N;3级法向预紧力为1 450 N;4级法向预紧力为1 852 N;5级法向预紧力为2 265 N;6级法向预紧力为3 132 N;7级法向预紧力为3 900 N。

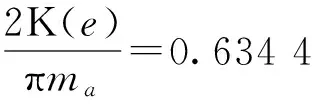
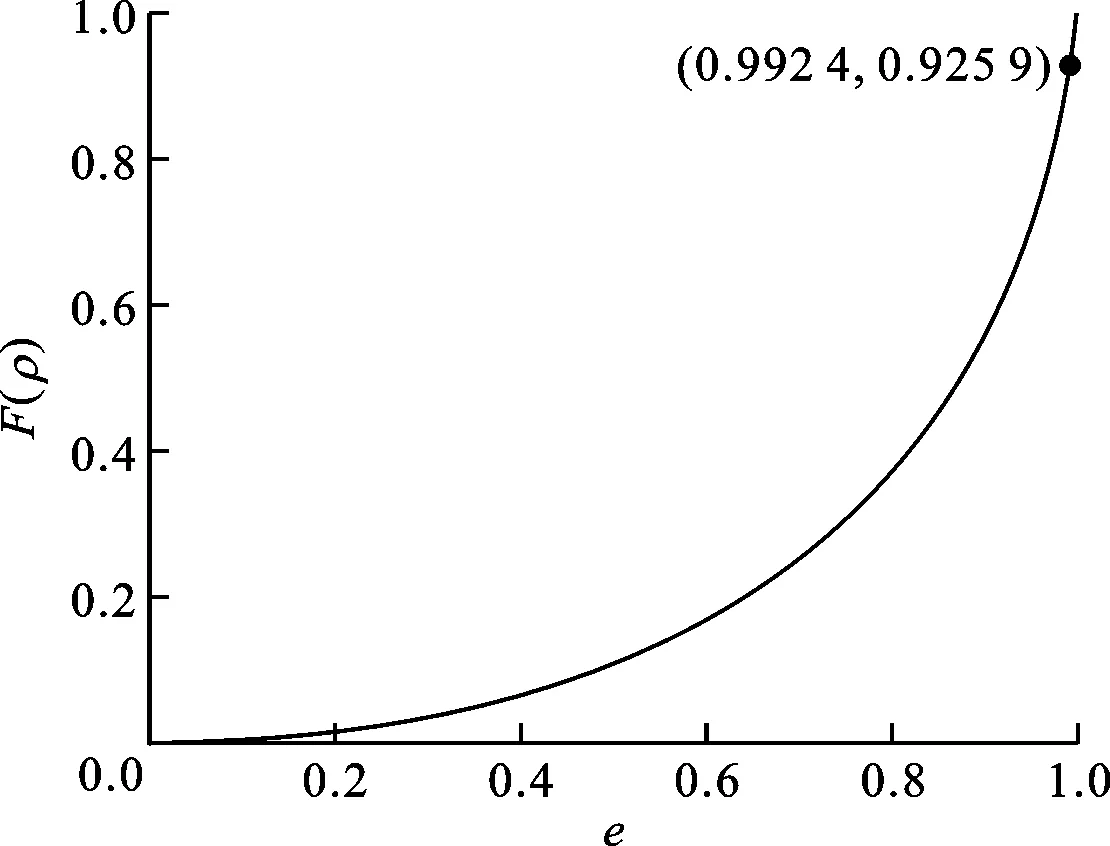
图4 根据式(44)反求解算的椭圆离心率

图5 按照式(51)计算的局部系数

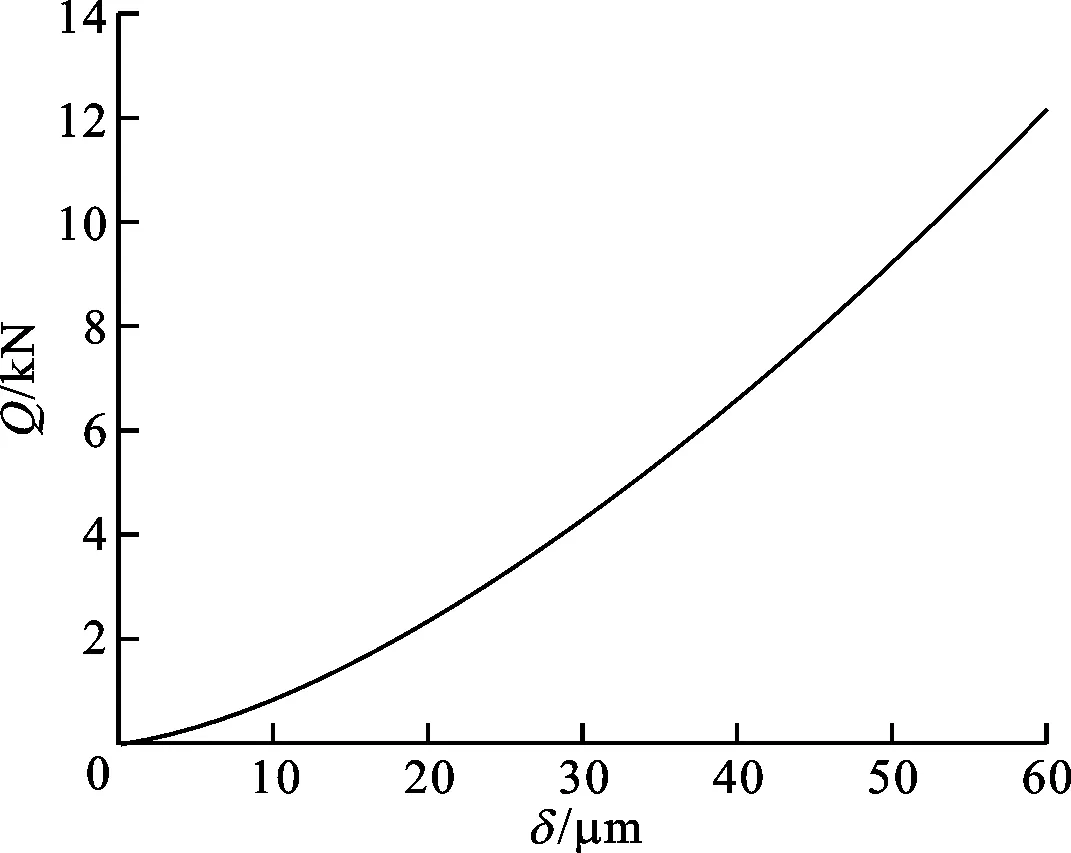
图6 工作载荷对滚珠压缩量的影响

3.1 工作载荷对滚珠压缩量的影响

图6显示了单个滚珠所受局部外加法向工作载荷Q对单个滚珠沿法线NM方向压缩量δ的影响,可见单个滚珠的压缩量随着工作载荷的增加而增加。

3.2 滚珠压缩量对滚珠刚度的影响

图7显示了单个滚珠沿法线NM方向的压缩量δ对滚珠法向接触刚度keq的影响,可见滚珠的法向接触刚度随着单个滚珠压缩量的增大而向上呈凸弧式增大,增大的幅度渐渐减小。

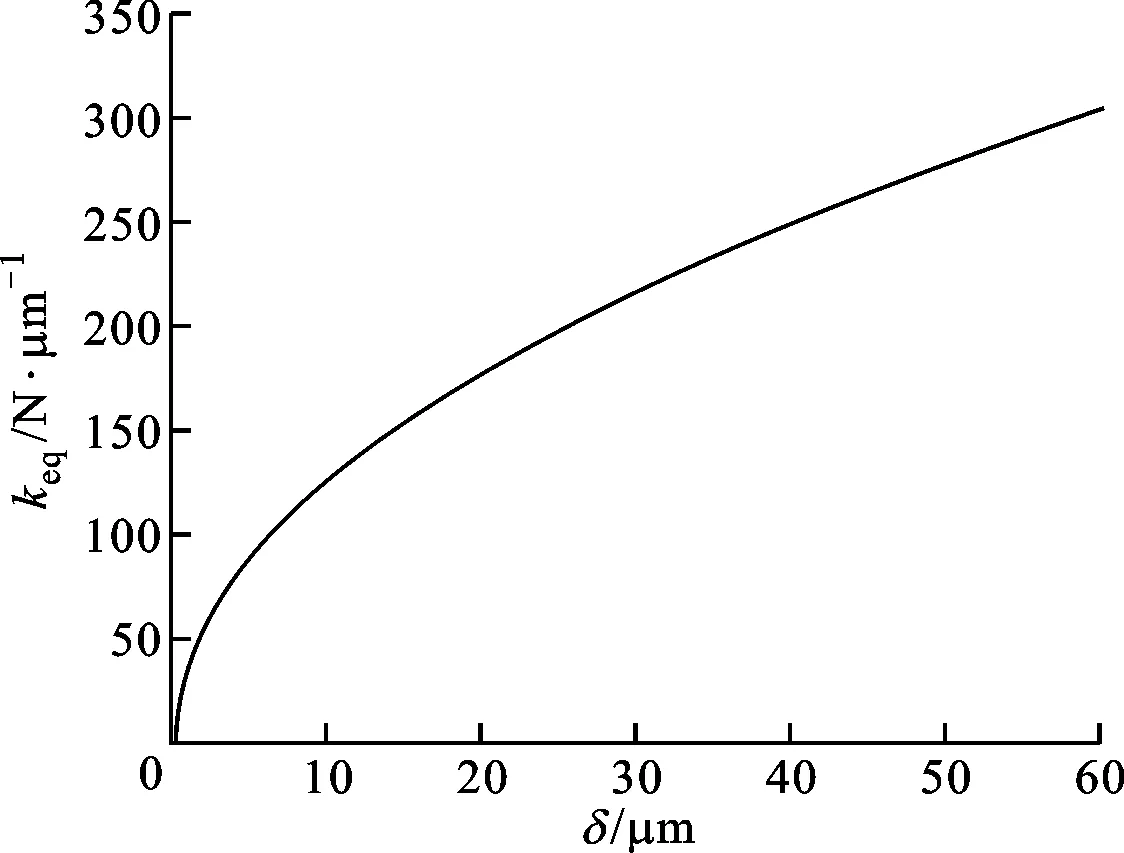
图7 滚珠压缩量对滚珠法向接触刚度的影响

3.3 工作载荷对滚珠法向接触刚度的影响

由式(3)得

(52)

将式(52)代入式(4)得

图8显示了单个滚珠所受局部外加法向工作载荷Q对滚珠法向接触刚度keq的影响,可见滚珠的法向接触刚度随着工作载荷的增加而向上呈凸弧式增大,增大的幅度逐渐减小。

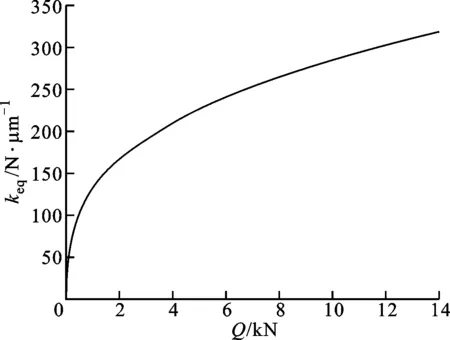
图8 工作载荷对滚珠法向接触刚度的影响

3.4 法向预紧力对滑块总压缩量的影响

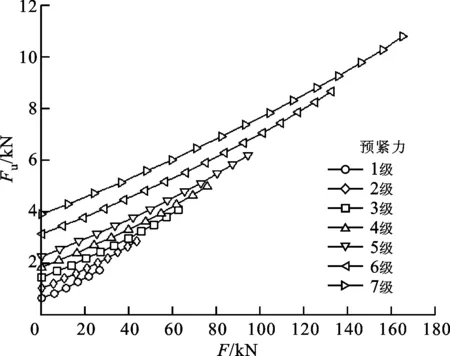
(a)工作总载荷-压缩力曲线

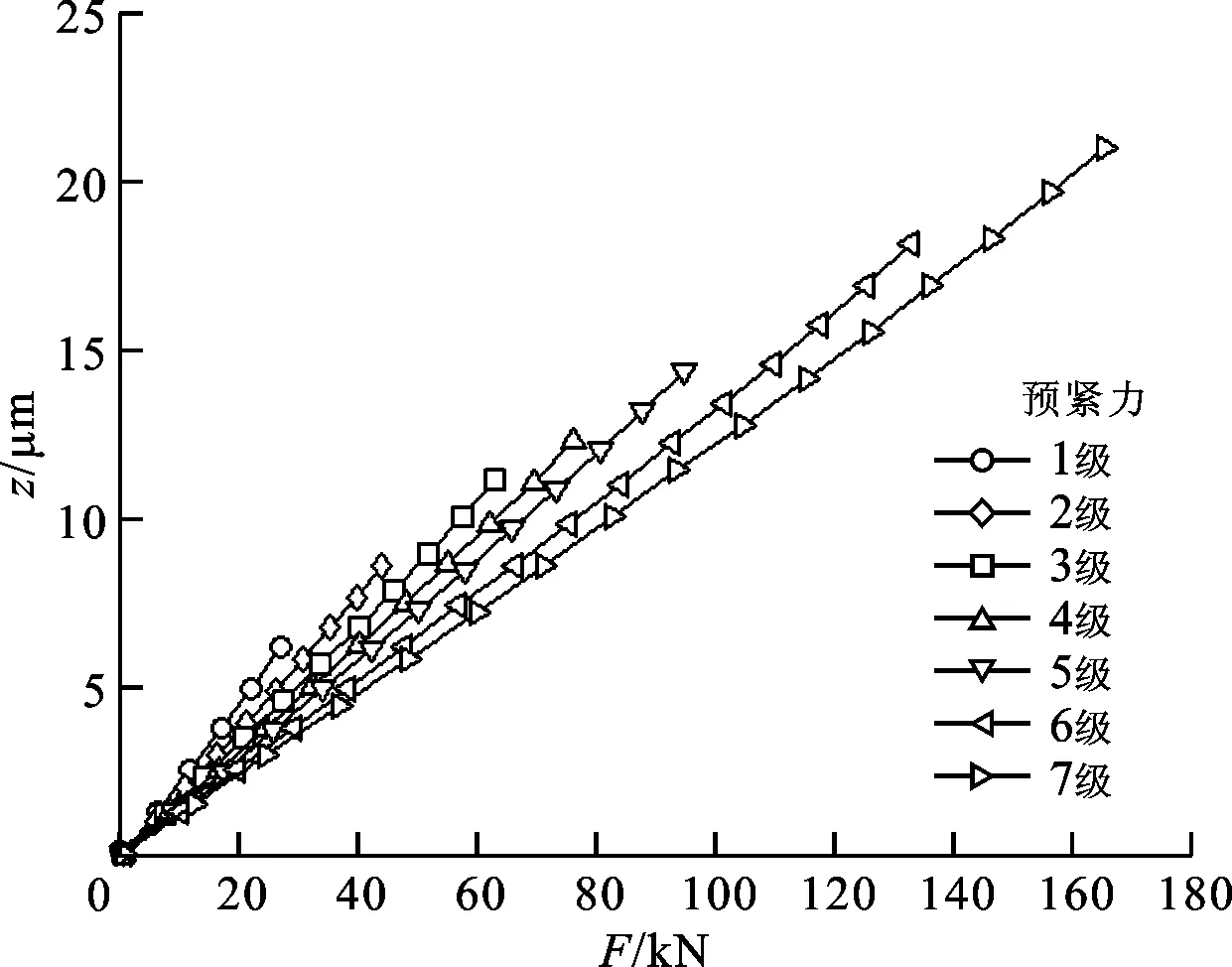
(b)工作总载荷-压缩量曲线图9 法向预紧力对滑块总压缩量的影响

当每列通道的工作滚珠总数N=10和接触角α=50°时,图9显示了法向预紧力F0对滑块相对于轨道沿外加法向工作总载荷F方向总压缩量z的影响。由图9b可见:函数z=z(F)在所考虑的有限闭区间[0,160 kN]内单调增加、可导且dz/dF≠0,印证了推导式(37)时所做的假设条件;随着外加法向工作总载荷的增大,滑块的总压缩量增大,在相同外加法向工作总载荷的作用下,滑块的总压缩量随着预紧力的增加(即预紧力等级的提高)而减小。

3.5 法向预紧力对滑块法向接触刚度的影响

当N=10和α=50°时,图10显示了F0对直线运动滚动导轨副滑块整体法向接触刚度kc的影响。由图10b可见,当F较小,即F∈[0,20 kN]时,F对第2～7级预紧力对应的滑块整体法向接触刚度无影响。由于接触面积是随机的,故接触变形不是定值,亦即接触刚度也不是定值,但在实际应用时,接触刚度必须是定值(图10b支持此观点)。根据图10b,F对第1级预紧力对应的滑块整体法向接触刚度有显著影响,这是因为第1级预紧力对应的最大F值为27.52 kN(见图10a),和所选择的F的最大值20 kN(见图10b)非常接近;远离F最大值的较小外加法向工作总载荷对滑块整体法向接触刚度无影响;当F接近其最大值时,F对滑块整体法向接触刚度有明显影响,且滑块整体法向接触刚度随着F的增加而减小。由图10a～10c可见,滑块整体法向接触刚度随着预紧力的增加而增加。

(a)工作总载荷的整个有效范围 (b)工作总载荷较小时 (c)工作总载荷较大时图10 法向预紧力对滑块法向接触刚度的影响

3.6 每列滚珠总数对滑块总压缩量的影响

图11显示了当F0=635 N和α=50°时,N对滑块在F方向的总压缩量z的影响,可见在相同F的作用下,滑块的总压缩量随着N的增加而减小。

3.7 每列滚珠总数对滑块法向接触刚度的影响

图12显示了当F0=635 N和α=50°时,N对直线运动滚动导轨副滑块整体法向接触刚度kc的影响,可见在相同F的作用下,kc随着N的增加而增大。

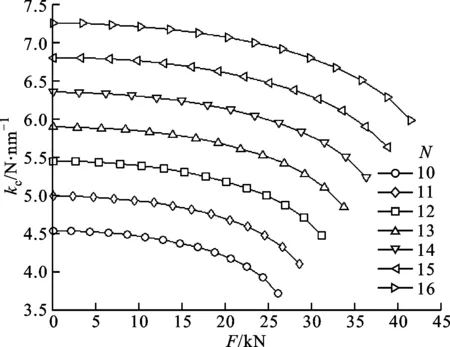
图12 每列通道滚珠总数对滑块法向接触刚度的影响

3.8 接触角对滑块总压缩量的影响

图13显示了当N=10和F0=635 N时,α对z的影响,可见滑块的总压缩量随着接触角的增加而略微减小。

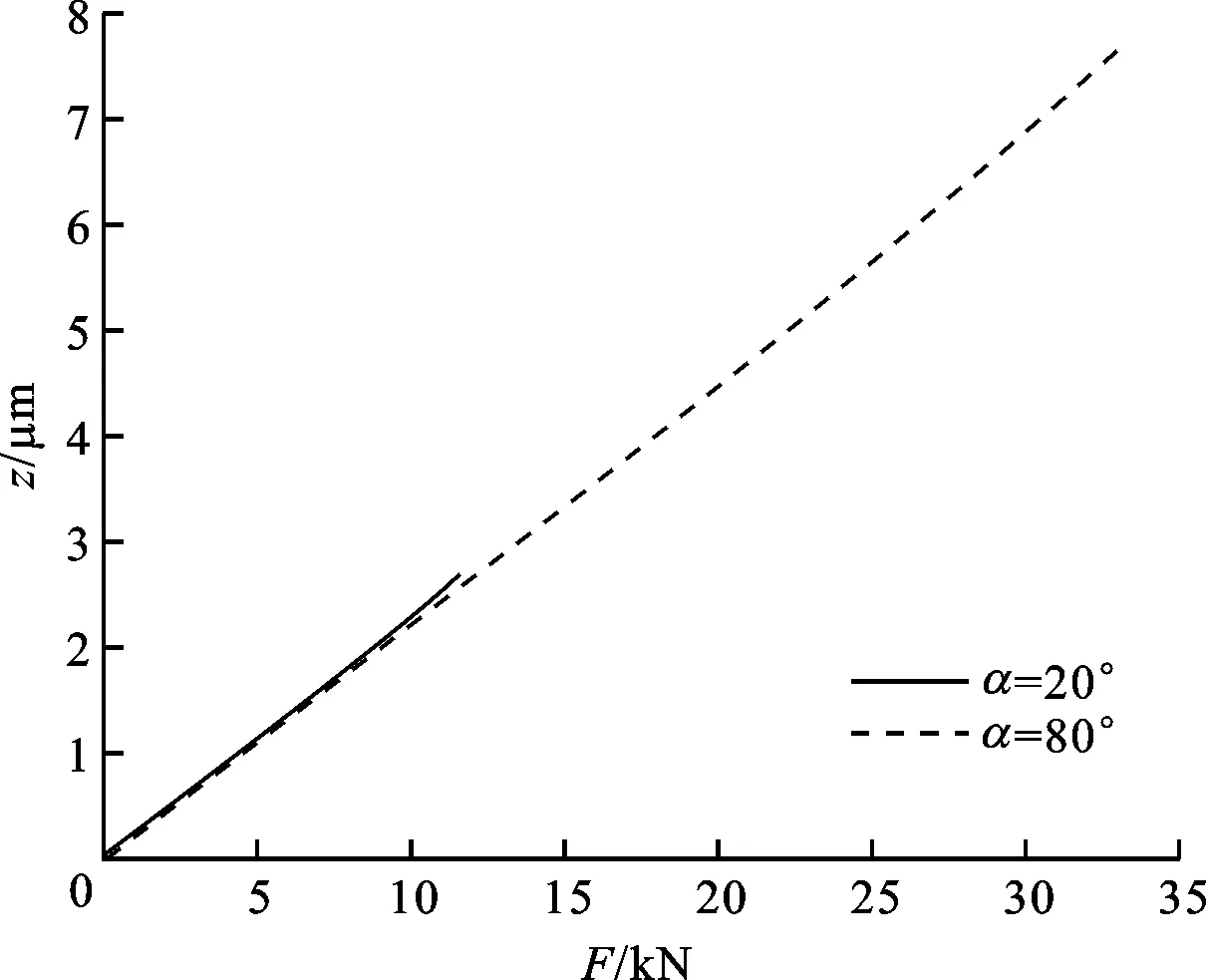
图13 接触角对滑块总压缩量的影响

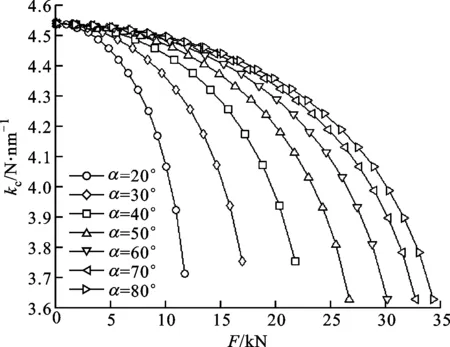
图14 接触角对滑块法向接触刚度的影响

3.9 接触角对滑块法向接触刚度的影响

图14显示了当N=10和F0=635 N时,α对kc的影响,可见滑块整体法向接触刚度随着接触角的增大而加大。

3.10 沟道曲率半径系数对单个滚珠特性的影响

沟道曲率半径系数是导轨副设计的一个重要参数,影响钢球与滚道间的密合程度以及钢球与滚道间的接触变形,从而影响导轨副的承载能力。图15显示了沟道曲率半径系数f对单个滚珠接触特性的影响。可以看出,随着f的增大,导轨副的承载能力减小(见图15a),单个滚珠的压缩量增加(见图15a和15b),滚珠的法向接触刚度减小(见图15b和15c),这主要是因为f影响密合度,f越小则密合度越大,因而在同样的负荷下接触面积越大,接触变形量越小,所能承受的载荷越大。

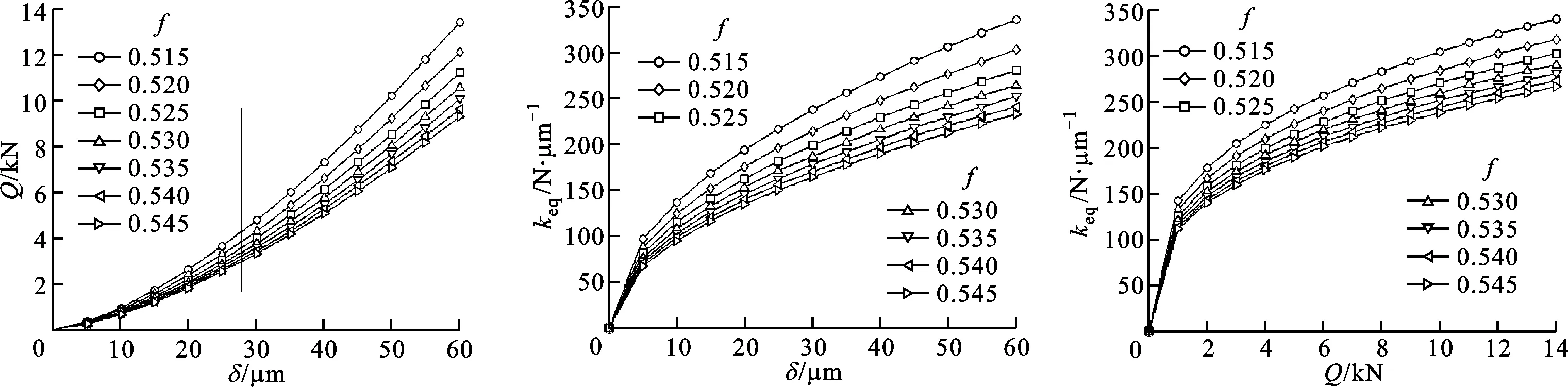
(a)对滚珠压缩量-工作载荷的影响 (b)对滚珠法向接触刚度-压缩量的影响 (c)对滚珠法向接触刚度-工作载荷的影响图15 沟道曲率半径系数对单个滚珠特性的影响

3.11 沟道曲率半径系数对滑块总压缩量的影响

图16显示了当N=10和F0=635 N时,f对滑块在F方向总压缩量z的影响。可以看出,滑块的总压缩量随着f的增加而增加。

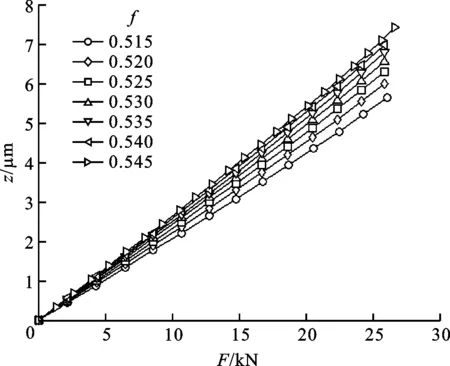
图16 沟道曲率半径系数对滑块总压缩量的影响

3.12 沟道曲率半径系数对滑块法向刚度的影响

图17显示了当N=10和F0=635 N时,f对直线运动滚动导轨副滑块整体法向接触刚度kc的影响,可见kc随着f的增大而减小。

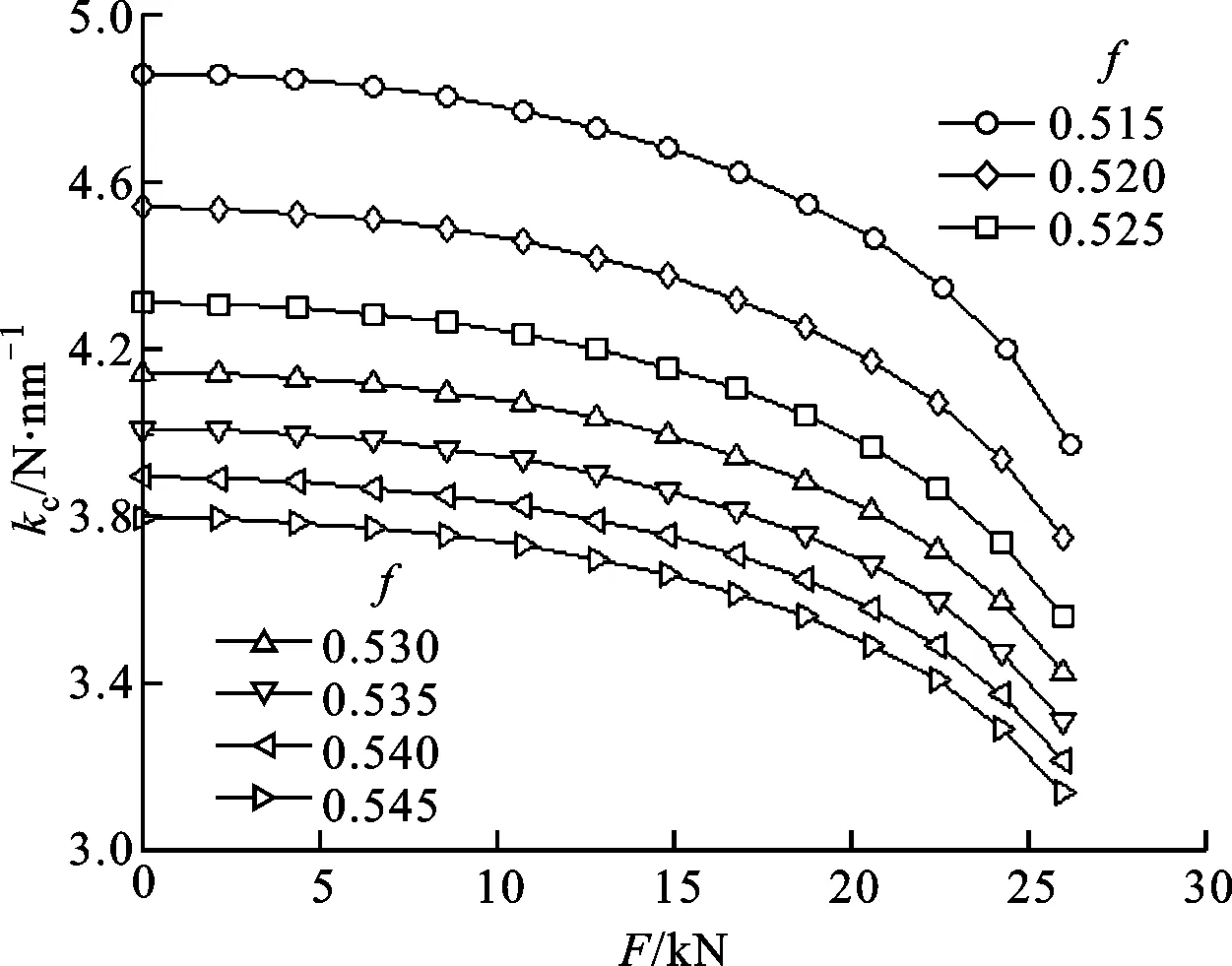
图17 沟道曲率半径系数对滑块法向刚度的影响

4 结 论

(1)滚珠的法向接触刚度随着单个滚珠压缩量的增大而向上呈凸弧式增大,随着沟道曲率半径系数的增大而减小;单个滚珠的压缩量随着沟道曲率半径系数的增加而增加。

(2)滑块的总压缩量随着外加法向工作总载荷、沟道曲率半径系数的增大而增大,随着预紧力、每列滚珠总数、接触角的增加而减小。当外加法向工作总载荷较小时,滑块整体法向接触刚度可视为常数。

(3)当外加法向工作总载荷接近最大外加法向工作总载荷时,外加法向工作总载荷对滑块整体法向接触刚度有明显影响,滑块整体法向接触刚度随着外加法向工作总载荷的增加而急剧减小。

(4)滑块整体法向接触刚度随着外加法向工作总载荷、沟道曲率半径系数的增加而减小,随着预紧力、每列滚珠总数、接触角的增加而增大。

[1] 李小彭, 王伟, 赵米鹊, 等. 考虑摩擦因素影响的结合面切向接触阻尼分形预估模型及其仿真 [J]. 机械工程学报, 2012, 48(23): 46-50. LI Xiaopeng, WANG Wei, ZHAO Mique, et al. Fractal prediction model for tangential contact damping of joint surface considering friction factors and its simulation [J]. Journal of Mechanical Engineering, 2012, 48(23): 46-50.

[2] 米良, 殷国富, 孙明楠, 等. 基于结合部动力学特性的立柱-主轴系统动力学模型研究 [J]. 农业机械学报, 2011, 42(12): 202-207. MI Liang, YIN Guofu, SUN Mingnan, et al. Column-spindle system dynamic model based on dynamic characteristics of joints [J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(12): 202-207.

[3] MI Liang, YIN Guofu, SUN Mingnan, et al. Effects of preloads on joints on dynamic stiffness of a whole machine tool structure [J]. Springer Journal of Mechanical Science and Technology, 2012, 26(2): 495-508.

[4] 李磊, 张建润, 刘洪伟. 直线滚动导轨副动态特性分析 [J]. 振动与冲击, 2012, 31(18): 111-114, 142. LI Lei, ZHANG Jianrun, LIU Hongwei. Dynamic characteristics of a linear motion guide [J]. Journal of Vibration and Shock, 2012, 31(18): 111-114, 142.

[5] 尹宜勇, 祝莉平, 贾志新, 等. 双丝杠与直线导轨结合部静刚度分析 [J]. 农业机械学报, 2012, 43(6): 202-206. YIN Yiyong, ZHU Liping, JIA Zhixin, et al. Static stiffness analysis of joint of double screw and linear guides [J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(6): 202-206.

[6] 朱坚民, 张统超, 李孝茹. 基于结合部刚度特性的滚珠丝杠进给系统动态特性分析 [J]. 机械工程学报, 2015, 51(17): 72-82. ZHU Jianmin, ZHANG Tongchao, LI Xiaoru. Dynamic characteristic analysis of ball screw feed system based on stiffness characteristic of mechanical joints [J]. Journal of Mechanical Engineering, 2015, 51(17): 72-82.

[7] HUNG J P. Load effect on the vibration characteristics of a stage with rolling guides [J]. Springer Journal of Mechanical Science and Technology, 2009, 23(1): 89-99.

[8] OHTA H, HAYASHI E. Vibration of linear guideway type recirculating linear ball bearings [J]. Elsevier Journal of Sound and Vibration, 2000, 235(5): 847-861.

[9] DHUPIA J S, ULSOY A G, KATZ R, et al. Experimental identification of the nonlinear parameters of an industrial translational guide for machine performance evaluation [J]. Journal of Vibration and Control, 2008, 14(5): 645-668.

[10]蒋书运, 祝书龙. 带滚珠丝杠副的直线导轨结合部动态刚度特性 [J]. 机械工程学报, 2010, 46(1): 92-99. JIANG Shuyun, ZHU Shulong. Dynamic characteristic parameters of linear guideway joint with ball screw [J]. Journal of Mechanical Engineering, 2010, 46(1): 92-99.

[11]JIANG Shuyun, ZHENG Shufei. A modeling approach for analysis and improvement of spindle-drawbar-bearing assembly dynamics [J]. Elsevier International Journal of Machine Tools & Manufacture, 2010, 50(1): 131-142.

[12]方兵, 张雷, 曲兴田, 等. 角接触球轴承动力学建模与实验 [J]. 农业机械学报, 2012, 43(6): 215-219, 225. FANG Bing, ZHANG Lei, QU Xingtian, et al. Dynamic modeling and experiment of angular contact ball bearing [J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(6): 215-219, 225.

[13]刘耀, 黄玉美. 机床滚珠导轨中圆柱面-球面结合面静特性分析及试验研究 [J]. 机械工程学报, 2013, 49(21): 25-30. LIU Yao, HUANG Yumei. Theoretical analysis and experimental study on static characteristics of the cylindrical-spherical joint surfaces of linear ball guide on machine tool [J]. Journal of Mechanical Engineering, 2013, 49(21): 25-30.

[14]刘静, 邵毅敏, 秦晓猛, 等. 基于非理想Hertz线接触特性的圆柱滚子轴承局部故障动力学建模 [J]. 机械工程学报, 2014, 50(1): 91-97. LIU Jing, SHAO Yimin, QIN Xiaomeng, et al. Dynamic modeling on localized defect of cylindrical roller bearing based on non-Hertz line contact characteristics [J]. Journal of Mechanical Engineering, 2014, 50(1): 91-97.

[15]胡建忠, 王民, 高相胜, 等. 双螺母定位预紧滚珠丝杠副轴向接触刚度分析 [J]. 机械工程学报, 2014, 50(7): 60-69. HU Jianzhong, WANG Min, GAO Xiangsheng, et al. Axial contact stiffness analysis of position preloaded ball screw mechanism [J]. Journal of Mechanical Engineering, 2014, 50(7): 60-69.

[16]卢宪玖, 王优强, 刘昺丽, 等. 考虑动态特性的角接触球轴承微观热弹流分析 [J]. 机械工程学报, 2014, 50(23): 104-111. LU Xianjiu, WANG Youqiang, LIU Bingli, et al. Analysis of micro-elastohydrodynamic lubrication of angular contact ball bearing considering dynamic characteristics [J]. Journal of Mechanical Engineering, 2014, 50(23): 104-111.

[17]王燕霜, 袁倩倩, 曹佳伟, 等. 特大型双排四点接触球轴承承载能力的研究 [J]. 机械工程学报, 2014, 50(9): 65-70. WANG Yanshuang, YUAN Qianqian, CAO Jiawei, et al. Research on static load-carrying capacity of large size double row four-point contact ball bearings [J]. Journal of Mechanical Engineering, 2014, 50(9): 65-70.

[18]杨家军, 韦振兴, 朱继生, 等. 行星滚柱丝杠副载荷分布及刚度计算 [J]. 华中科技大学学报: 自然科学版, 2011, 39(4): 1-4. YANG Jiajun, WEI Zhenxing, ZHU Jisheng, et al. Calculation of load distribution of planetary roller screws and static rigidity [J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2011, 39(4): 1-4.

[19]卓耀彬, 周晓军. 高速滚珠关节轴承的动力学特性分析 [J]. 机械工程学报, 2015, 51(5): 37-46. ZHUO Yaobin, ZHOU Xiaojun. Dynamic characteristic analysis of high-speed spherical ball bearing [J]. Journal of Mechanical Engineering, 2015, 51(5): 37-46.

[20]卓耀彬, 周晓军. 游隙对双列调心球轴承静力学性能影响及游隙控制分析 [J]. 农业工程学报, 2013, 29(19): 63-70. ZHUO Yaobin, ZHOU Xiaojun. Analysis of effect of clearance on static mechanical behavior for double row self-aligning ball bearing and control of clearance [J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(19): 63-70.

[21]田红亮, 方子帆, 朱大林. 赫兹点接触133年 [J]. 三峡大学学报: 自然科学版, 2014, 36(2): 88-97. TIAN Hongliang, FANG Zifan, ZHU Dalin. 133 years of Hertz point contact [J]. Journal of China Three Gorges University: Natural Sciences, 2014, 36(2): 88-97.

[22]王民, 乐兵兵, 裴二阳. 基于Hertz接触的滚珠直线导轨副接触刚度建模与分析 [J]. 北京工业大学学报, 2015, 41(8): 1128-1132, 1150. WANG Min, LE Bingbing, PEI Eryang. Contact stiffness modeling and analysis of linear ball guides based on Hertz contact theory [J]. Journal of Beijing University of Technology, 2015, 41(8): 1128-1132, 1150.

[23]孙伟, 孔祥希, 汪博, 等. 直线滚动导轨的Hertz接触建模及接触刚度的理论求解 [J]. 工程力学, 2013, 30(7): 230-234. SUN Wei, KONG Xiangxi, WANG Bo, et al. Contact modeling and analytical solution of contact stiffness by Hertz theory for the linear rolling guide system [J]. Engineering Mechanics, 2013, 30(7): 230-234.

[本刊相关文献链接]

田红亮,余媛,陈甜敏,等.考虑表面粗糙度和几何曲率的两球体接触问题[J].2016,50(3):1-7.[doi:10.7652/xjtuxb 201603001]

刘雨薇,张卫正,叶福浩.单个微凸体接触过程中的闪点温度研究[J].2016,50(3):90-93.[doi:10.7652/xjtuxb201603 014]

王庆朋,张力,尚会超,等.考虑应变硬化的混合弹塑性接触模型[J].2016,50(2):132-137.[doi:10.7652/xjtuxb201602 022]

田红亮,陈甜敏,郑金华,等.平行轴圆柱副接触分析[J].2016,50(1):8-15.[doi:10.7652/xjtuxb201601002]

蒲伟,王家序,杨荣松,等.重载下准双曲面齿轮传动界面润滑机理分析[J].2015,49(11):55-61.[doi:10.7652/xjtuxb 201511010]

王东,徐超,万强.弹塑性接触粗糙表面切向载荷-位移模型[J].2015,49(11):122-127.[doi:10.7652/xjtuxb201511020]

刘伟强,张进华,洪军,等.椭圆抛物体形微凸体弹性接触力学模型[J].2015,49(10):34-40.[doi:10.7652/xjtuxb201510 006]

冯燕,俞小莉,刘震涛.应用热弹塑性理论的结合部法向载荷分形模型[J].2015,49(9):18-23.[doi:10.7652/xjtuxb2015 09004]

周安安,陈天宁,王小鹏,等.自仿射接触点及其在分形接触理论中的应用[J].2015,49(6):8-15.[doi:10.7652/xjtuxb201506002]

陈兵奎,梁栋,彭帅,等.共轭曲线齿轮啮合管齿面的几何及接触特性分析[J].2015,49(3):85-94.[doi:10.7652/xjtuxb 201503015]

(编辑 葛赵青)

Normal Contact Mechanics Model of Linear Motion Rolling Guideway Pair

TIAN Hongliang,ZHENG Jinhua,CHEN Tianmin,YU Yuan,ZHANG Yi

(College of Mechanical and Power Engineering, China Three Gorges University, Yichang, Hubei 443002, China)

Based on the theory of Hertz point contact forming elliptic contact region, a movable joint interface’s normal contact mechanics model of linear motion rolling guideway pair is established considering the external normal total load and preload. The elliptic eccentricity is revolved using the first and second complete elliptic integrals. An implicit function equation relating a ball’s oblique low compression force with the external normal total working load is obtained. Particularly, some analytic expressions about one ball’s normal compression deformation, one ball’s normal contact rigidity, the carriage’s total compression deformation and overall normal contact rigidity are deduced. The digital simulation results show that one ball’s compression deformation increases with the groove curvature radius coefficient; the ball’s normal contact rigidity increases upwards protrusively with the ball’s compression deformation, but decreases with the groove curvature radius coefficient; and the carriage’s total compression deformation increases with the external normal total working load or groove curvature radius coefficient, but decreases with the increasing of the preload, the ball’s total number per column or contact angle. When the external normal total working load is much smaller than the maximum value, the carriage’s overall normal contact rigidity is constant. When the external normal total working load is close to the maximum, it has a notable impact on the carriage’s overall normal contact rigidity, i.e., the latter decreases dramatically with the increase of the former. The carriage’s overall normal contact rigidity increases with the increase of the preload, the ball’s total number per column or contact angle, but declines with the external normal total working load or groove curvature radius coefficient. Constructing the normal contact mechanics model of joint interface helps analyze the actual contact states between movable contact surfaces of linear motion rolling guideway pair.

numerical control machine; rolling guideway pair; ball; carriage; rail; normal working load; normal preload

10.7652/xjtuxb201605001

2015-10-18。 作者简介:田红亮(1973—),男,博士,副教授;张屹(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(51275273)。

时间:2016-03-02

http:∥www.cnki.net/kcms/detail/61.1069.T.20160302.2014.012.html

TH113.1

A

0253-987X(2016)05-0001-11