理解数学关注学情优化教法——谈谈用频率估计概率的教学

理解数学关注学情优化教法——谈谈用频率估计概率的教学

向利平

与统计与概率板块的诸多教学内容一样，老师们对用频率估计概率这一内容的教学没有引起重视。一种现象是，教学时常常要学生自读课本，然后告诉学生“通过大量重复试验获得的随机事件发生的频率可以作为该随机事件发生的概率”，最后花大量时间进行题型训练。另一种现象是，老师本身对与教学内容相关的背景知识理解不到位，有一些错误认识，导致课堂中常常出现一些错误的做法或说法。本文拟从教学内容的相关背景知识、教学目标定位等方面谈谈自己的认识和理解，并提出一个教学设计案例，以求抛砖引玉。

一、与教学内容相关的背景知识

1.概率

现实世界中有确定和不确定两类现象，我们把不确定现象称作随机现象。随机现象是否一定发生是不确定的，但随机现象发生的可能性是存在的。为此，人们常常关心这样的问题：随机现象发生的可能性是否有大有小呢？除了定性的有大有小，是否还可以定量地刻画呢？

研究随机现象的基本方法是随机试验，随机试验的结果是不确定的，每种可能的结果称为随机事件。在一次随机试验中，一个随机事件是否发生是没有什么规律的，但我们不断地重复做同一个试验时，随着试验次数的增多，随机事件发生的规律性便呈现出来了，我们把这种规律性叫做随机现象的统计规律。概率论就是研究这种统计规律的数学分支。

随机事件发生的可能性有大有小。为了精确地定量刻画随机事件发生的可能性大小，数学中引入了概率这一概念。概率就是随机事件发生的可能性大小的数量表达。

现实生活中的随机现象是千姿百态、丰富多彩的。为了研究的方便，我们将随机现象分成一些基本类型。比如，前面学习了的用列举法求概率的古典概型，课本例题和练习题中涉及的用转盘及各分区的面积求概率的几何概型，等等。现实世界中还有很多随机现象，我们不能直接通过计算得到某一随机事件发生的概率。比如，抛一枚图钉，针尖着地的概率，某人站在篮球场的罚球线上投篮投进篮筐的概率，等等。用频率估计概率可以解决这类不能直接通过计算求得的概率问题。

2.用频率估计概率

以抛掷硬币试验为例，如果仅做一次抛掷1000次硬币的试验，我们可以计算出硬币正面朝上的频率，但无法谈正面朝上频率的规律。但如果我们继续做第2次、第3次直到第k次试验，每次抛掷硬币的次数n足够多，正面朝上频率的规律就表现出来了，它总在一个定值附近波动。从这k次抛掷试验的结果对比中，我们还可以发现，一般来说抛掷硬币的次数n越多，正面朝上的频率与那个定值相差越小。也就是说，虽然n次试验所得到的频率各不相同，但只要n足够大，频率就会非常接近一个固定的值。这种规律称作频率的稳定性。频率的这种稳定性说明了一个事件发生的可能性有大小可言，这也使得用频率测量概率成为可能。事实上，概率论中的大数定律是已经证明过了的：当重复试验次数足够多时，某一事件出现的频率与概率有较大偏差的可能性很小。

理解用频率估计概率要注意以下几点：一是可以用大量重复试验中随机事件的频率作为随机事件概率的估计值；二是频率不能等同于概率，两者有本质区别:频率依赖于试验，而概率是随机事件本身固有的属性，是客观的，不依赖于具体试验而存在；三是在不同的n次试验中，即使试验次数n相同，但同一事件发生的频率也可能不相同，因此不能误认为试验1000次获得的结果就一定比试验100次获得的结果更准确。

3.随机试验设计及数据分析

历史上很多人做过成千上万次抛硬币试验，湘教版和人教版教材都列出了一些著名试验的结果。下表是人教版教材中列出的几个著名试验。

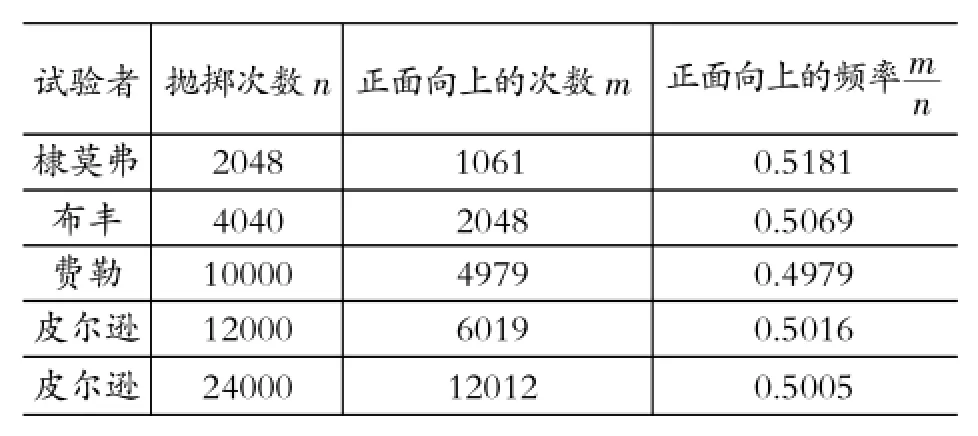
试验者抛掷次数n正面向上的次数m棣莫弗2048 1061 0.5181布丰4040 2048 0.5069费勒10000 4979 0.4979皮尔逊12000 6019 0.5016皮尔逊24000 12012 0.5005正面向上的频率m n

对以上这些试验的认识应把握如下几点：

①这个表列出了4个人所做的5次试验，每一次抛掷试验的次数为n，这里面的两个次数的意义是不一样的；

②当抛掷次数n很大时，从5次试验的结果看，硬币正面向上这一随机事件发生的频率均是在固定值0.5上下波动；

③随着抛掷次数n的不断增大，正面向上的频率越来越接近0.5这个固定值；

抛掷硬币的问题属于古典概型，我们知道正面向上的概率是0.5。正因为事先知道正面向上的概率是0.5，历史上很多人便利用抛掷硬币试验研究频率与概率间的关系。抛掷硬币试验实际上有两个目的，一是探究大量重复试验中随机事件发生的频率的统计规律，发现频率的稳定性；二是验证可以将大量重复试验的频率作为概率的估计值。这两个目的实际上也是本节课教学所要达成的目标。

要发现频率的稳定性，当然需要做很多次“n次试验”，对很多次“n次试验”获得的随机事件发生的频率值进行收集、整理并作分析，看看这很多个频率值是不是具有稳定性，看看这很多个频率值在哪个固定值附近波动。这很多次“n次试验”及数据分析的方式如下表所示。

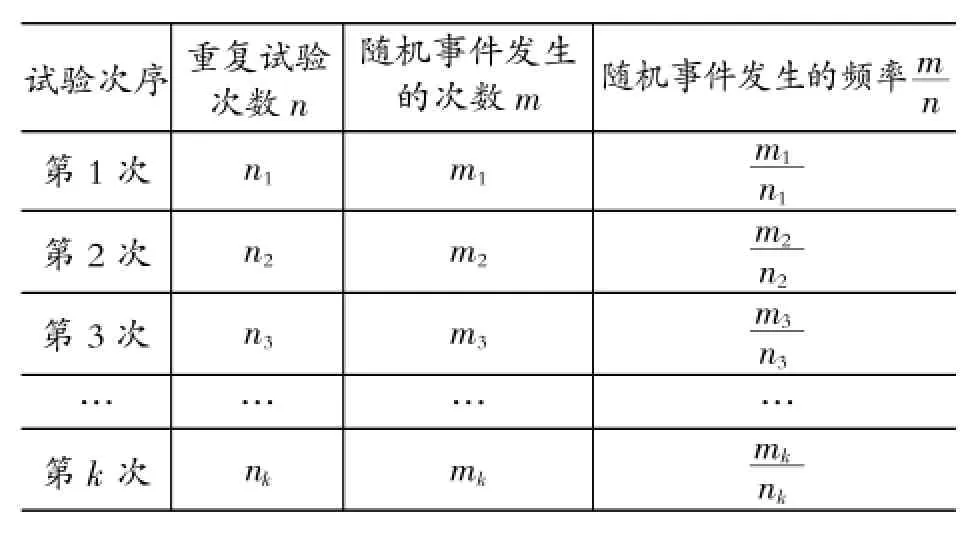
试验次序重复试验次数n 随机事件发生的频率m n随机事件发生的次数m第1次n1m1m1n1第2次n2 n2m2第3次n3m3……m3 n3……第k次nkmkmk m2 nk

二、本节课的目标定位

仅从知识目标而言，课程标准对该内容的要求并不高，仅一句话：知道通过大量的重复试验，可以用频率来估计概率。但从理解数学，从整个统计与概率的过程与方法目标的角度看，本教学内容有很重要的价值。结合教学内容的特点，本节课的教学目标可作如下定位：

引导学生经历提出问题，设计试验，收集数据，整理和分析数据的过程；探究大量重复试验中随机事件发生的频率的统计规律，发现频率的稳定性，体会频率与概率的关系。信服地接受“通过大量的重复试验，可以用频率来估计概率”。

三、教学过程的一些困难及突破

通过前面的背景知识分析我们知道，要获得理想的结论，需做要多轮次的足够次数的随机试验。但课堂的时间是有限的，要达到多轮次的足够次数的试验显然不可能。因此，我们可将全班同学分成若干（比如说14）个试验小组，各组在相同条件下做一定次数（比如说50次）的重复试验，在收集和整理数据时采用累计的方式，就可以得出14轮次的14个数据，且第14轮次的试验次数可达到700。

由于是将全班同学分成若干个小组合作进行同一个试验，因此试验的规则、试验中的注意事项等均需要在试验前进行很好的示范和统一。

教材中提供的抛掷硬币试验虽然是很经典的试验，但由于学生事先已经知道了试验结果，观客上不容易引发学生的探究欲望，容易引发应付的情绪，甚至应付式的谎报数据。因此，有必要将问题进行改进，使学生在试验前并不知道试验的结果，但试验结束后又可进行验证。

试验结果与预设的结果难免存在一定程度的偏差，会出现哪些偏差，对出现的数据偏差如何解释，教师在教学设计时应做好思考和预设。

四、教学设计案例

（一）复习用列举法求概率，提出新的问题。

问题1：不透明的布袋中有20个玻璃珠，其中黄色的15个，红色的5个，每个玻璃珠除了颜色不同外都一样。从中任意摸出一个玻璃珠，摸到红色玻璃珠的概率是多少？

问题2：（出示事先准备的不透明的布袋，内装4个黄色玻璃珠和1个红色玻璃珠）这个袋子里装有黄色玻璃珠和红色玻璃珠共5个，但我不知道里面有多少个黄色玻璃珠和红色玻璃珠。现在老师想知道从袋中任意摸一个玻璃珠，摸到红色玻璃珠的概率是多少。请同学们帮我想想办法，怎么办？

（二）分析问题，设计试验方案，分组操作试验。

引导学生分析问题2：这个随机事件共有5种可能的结果，但我们不知道有哪5种可能的结果，所以不能通过计算得出摸到红色玻璃珠的概率，看来只好进行试验了。

问题3：这个试验该怎么做呢？做试验的过程中要注意些什么？需要记下哪些数据？（学生讨论之后教师小结，提出试验要求）

学生活动：将全班同学分成14个小组，每个小组分别进行50次摸玻璃珠试验，并记下这50次试验中摸到红色玻璃珠的次数。

（三）整理并分析试验数据，体会“随着试验次数的增加，一个事件出现的频率，总在一个固定数的附近波动，显示出一定的稳定性”。

1.引导学生将试验的数据累计并汇总，完成下面的统计表和散点统计图。

师生交流达成如下共识：为了节省试验的时间，把第1组同学的50次摸玻璃珠试验作为第一轮试验，将数据填在第1列中；把第1、2组同学的100次摸玻璃珠试验作为第二轮试验，将数据填在第2列中；把第1、2、3组同学的150次摸玻璃珠试验作为第三轮试验，将数据填在第3列中。这样，我们就相当于做了12个轮次的试验。摸到红玻璃珠频率

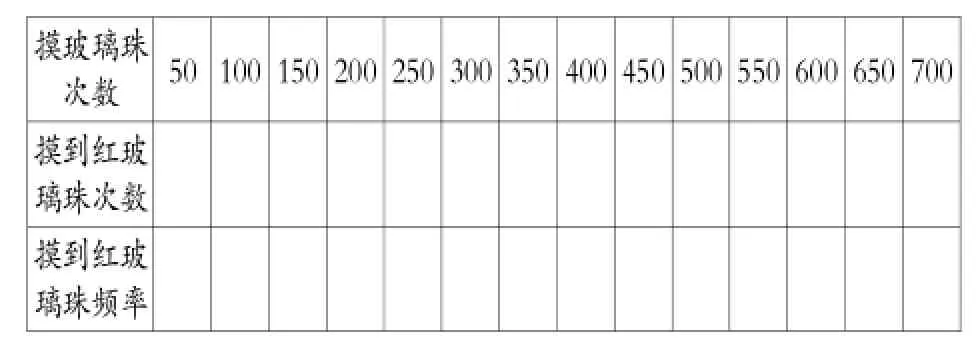
摸玻璃珠次数50 100 150 200 250 300 350 400 450 500 550 600 650 700摸到红玻璃珠次数摸到红玻璃珠频率

2.观察统计图表，思考并回答下列问题：

①随着摸玻璃珠试验轮次的增加，摸到红玻璃珠的频率值有什么规律？

②请同学们打开装有玻璃珠的袋子，看看里面有几个黄色玻璃珠，几个红色玻璃珠。用前面所学的列举法计算，摸到红色玻璃珠的概率是多少。

③比较一下，随着摸玻璃珠次数的增加，摸到黄色玻璃珠的频率值与摸到黄色玻璃珠的概率有什么关系？

（四）归纳小结，得出新知识。

教师归纳并小结：实际上，人们从长期的实践中观察到，对一般的随机事件，在做大量重复试验时，随着试验次数的增加，一个事件出现的频率总在一个固定值附近波动，显示出一定的稳定性。这一统计规律是由瑞士数学家雅各布·伯努利最早阐明，数学上称其为大数定律。值得一提的是，伯努利家族前后三代共出了13位大数学家和大物理学家。

正是有了这一规律，我们便可以用大量重复试验所得的随机事件发生的频率作为该事件发生的概率的估计值。

（五）提出新问题，促进学生认知水平的深化。

进一步观察统计图表，思考并回答下列问题：

1.1000次摸玻璃珠试验获得的频率值是否一定比500次摸玻璃珠试验获得的频率值更接近该事件发生的概率？

2.要获得较准确的概率估计值，在收集试验数据时应注意些什么？

（六）练习巩固，应用新知。

在同样条件下对某种小麦种子进行发芽实验,统计发芽种子数，获得如下频数分布表。

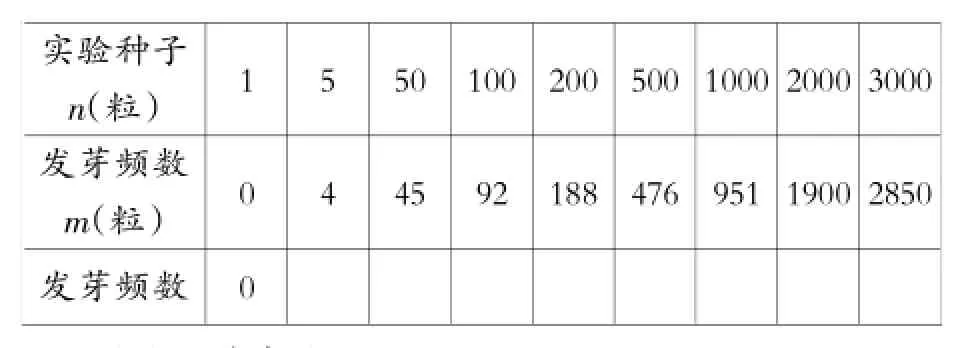
实验种子n（粒）1550100200500 1000 2000 3000发芽频数m（粒）044592188476951 1900 2850发芽频数0

（1）计算表中的各个频数；

（2）估计该小麦种子的发芽概率；

（3）如果播种该种小麦每公顷所需麦苗数为4181818棵，种子发芽后的成秧率为87%，该小麦种子的千粒质量为35g，那么播种3公顷该种小麦，估计约需麦种多少kg？

（七）小结与作业布置（略）。

（作者单位：长沙市岳麓区教研室）