并列型PA 6/PET复合扁平纤维挤出成形工艺的数值模拟

宁 宁，甘佳佳，冯 培，陈 革

(东华大学 纺织装备教育部工程研究中心，上海 201620)



并列型PA 6/PET复合扁平纤维挤出成形工艺的数值模拟

宁 宁，甘佳佳，冯 培，陈 革

(东华大学 纺织装备教育部工程研究中心，上海 201620)

以聚酰胺6(PA 6)和聚对苯二甲酸乙二醇酯(PET)两种聚合物为原料，利用Polyflow软件建立并列型PA 6/PET复合扁平纤维挤出成形的模型，模拟在不同流量、不同纺丝温度下纤维挤出成形的过程，分析在此过程中纤维横截面形状系数及丝条温度的变化情况。结果表明：在复合扁平纤维纺丝中，两种流体入口流量比的变化会引起共挤出界面位置和形状的变化；PA 6/PET复合扁平纤维形状系数随着PA 6:PET流量比的增大而减小，随着总流量的增加而增大，而丝条温度降低的趋势变缓；复合扁平纤维的形状系数随着纺丝温度升高而降低。

聚己内酰胺纤维 聚对苯二甲酸乙二酯纤维 复合纺丝 扁平纤维 形状系数 数值模拟

在合成纤维成形过程中，采用非圆形孔的喷丝板，制取各种不同截面形状的纤维或中空纤维以改善纤维的手感、光泽等性能，这种纤维称为异形纤维[1]。进入20世纪80年代以来，异形纤维生产向异形复合化、中空化和多功能化方向发展。其中，复合异形纤维是将两种具有不同物理性质的高聚物熔体从同一个喷丝孔中喷出而形成在断面上由两种组分结合形成的纤维[2]。

作者选取并列型聚己内酰胺/聚对苯二甲酸乙二醇酯(PA 6/PET)复合扁平纤维作为模拟计算的研究对象，运用Polyflow专用软件研究其在熔融纺丝过程中的挤出成形过程。界面不稳定性和异形度是影响异形共挤出成形制品性能的重要因素[3]，研究纺丝参数的变化对异形度的影响具有重要的理论参考价值。

1 理论模型和几何模型

1.1 理论模型的建立

(1)非等温流动的控制方程有[4]：

连续性方程：

▽V=0

(1)

动量方程：

-▽p+▽τ=0

(2)

能量方程：

ρCPV▽T=Kd▽2+τ▽V

(3)

式中： V为速度矢量；P为静压力； τ为应力张量； ρ为密度；CP为比热容； Kd为导热系数；T为温度。

(2)本构方程采用非等温Plan-Thien-Tanner模型，是由时间-温度等温叠加算法转化而来：

(4)

式中：T1，T2为上、下随流时间导数；ε，ξ分别为控制材料拉伸性能和剪切性能的材料参数；λ为形变速率张量；η1为模型的黏度系数。

(3)热流边界条件：

Q=qc+α(T-Tα)+σ[(T+T0)4-(Tσ+T0)4]

(5)

式中：Q是总热流量；qc是与温度无关的热通量；α是热对流系数；T是在边界的温度；Tα是参考温度的对流热交换；σ[(T+T0)4-(Tσ-T0)4]是史蒂芬-波兹曼定律表示辐射换热。

(4)表面张力(fn)：

(6)

式中： σ为表面张力系数；R为曲率半径。

(5)多组分分界面条件：边界条件确定了不同子任务区域连续处两边的连续性。分界面需要满足以下条件，运动学条件：在界面上速度场是连续的，即熔体流动没有穿透界面，界面上两种熔体的切向速度相等；动力学条件：界面两侧的切向应力和法向应力是连续的，即两侧的应力相等。

1.2 几何模型的建立

采用两组分复合扁平实体模型，扁平微孔的尺寸宽为0.000 3 m，长为0.004 m，复合熔体从喷丝微孔中挤出过程分2个区域：喷丝微孔内流动区(0.001 5 m)和挤出喷丝孔后的挤出成形区(0.6 m)如图1所示。

图1 复合扁平模型Fig.1 Composite flat modelSD1—计算区域1；SD2— 计算区域2

采用正六面体小单元对三维几何模型划分网格，由于喷丝孔出口附近熔体细流直径和运动速度变化较大，所以把网格加密，有利于计算收敛和获取更多的速度分布调整信息[4]，其有限元网格划分模型如图2所示。

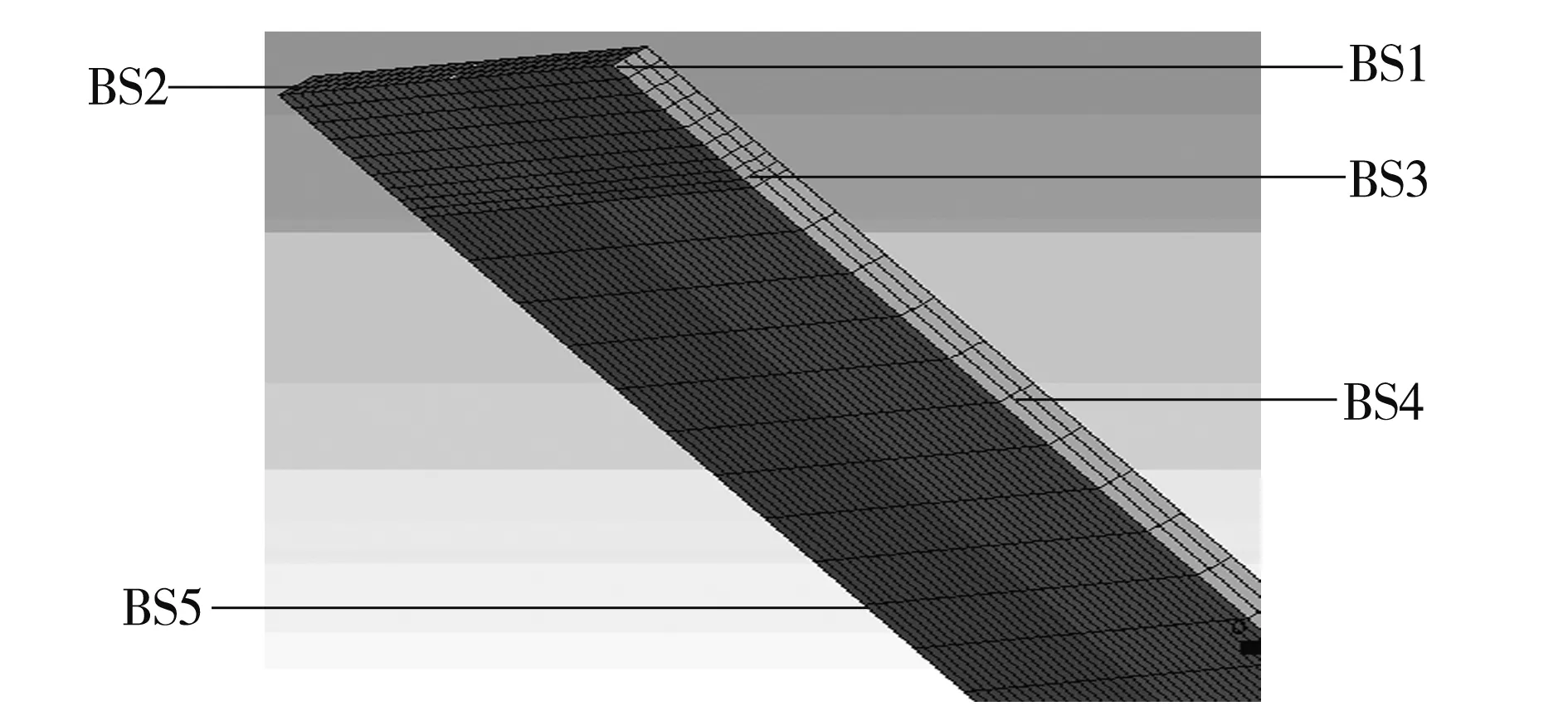
图2 有限元网格划分模型Fig.2 Finite element mesh modelBS1—PET入口；BS2—PA 6入口；BS3—喷丝孔壁面； BS4—自由面(纤维表面)；BS5—PET与PA 6的交界面

2 数值模拟

模拟环境设置包括材料特性参数设置和边界条件设置，在设置两个边界条件时均需要对自由面的边进行网格重划分。

2.1 材料参数设置

模拟计算参数包括材料流变特性参数和熔融纺丝工艺条件参数[5-8]，具体参数见表1，表2。其中，n为非牛顿指数，η0为零剪切黏度，t为松弛时间，k为热传导率，D为扁平喷丝孔长度，W为扁平喷丝孔宽度，Ta为喷丝孔入口温度，Tb为冷却空气温度，L0为微孔长度，L1为计算区域2长度。

表1 材料流变性参数

Tab.1 Rheological parameters of raw material

项目参 数PA6PETn0．750．66t/s0．020．012η0/Pa·s75210ρ/(kg·m-3)9731268k/(W·m-1·k-1)0．200．21Cp/(J·kg·k-1)3332．53453．0

表2 熔融纺丝工艺参数

Tab.2 Melt spinning process parameters

项 目 参 数D/m4×10-3W/m0．3×10-3Ta/℃285Tb/℃20L0/m1．5×10-3L1/m0．6

2．2 模拟边界条件

模拟计算边界条件包括流动边界条件和热边界条件[8-9]。由于模型适用非等温黏弹性的流变过程，由很多非线性变量组合而成，所以必须对网格重置以保证计算的收敛性。

2.2.1 流动边界条件

各个物理边界设置如图 2 所示。其中，进口(BS1，BS2):设定入口流量；壁面(BS3):喷丝孔壁面，设定Vn等于Vs为0(Vn，Vs分别为法向速度和切向速度)；自由面(BS4):设定表面张力系数，由于自由面变形，需要进行网格重置；分界面(BS5):设定表面张力系数；出口:设定fn为0，fs为0(fn，fs分别为法向力、切向力)。

2.2.2 热边界条件

进口(BS1、BS2) :设定入口温度；壁面(BS3):认为温度恒定，即不传热；自由面(BS4):表面温度需要设定热通量(即对流传热)；分界面(BS5)：设定热通量(即对流传热)。

3 模拟结果分析

选取不同流量、不同纺丝温度熔体纺丝工艺条件作为模拟方案，采用纤维横截面的形状系数(L2/S)(L为纤维横截面的周长，S为纤维横截面的面积)来评定扁平纤维的异形度。

3.1 流量变化

为了研究流量对复合异形纤维L2/S的影响，采取两种方案，方案一：流量不变，改变两种组分之间的流量比；方案二：复合组分中的一种组分流量不变，另一种组分流量增加。

方案一：多组分纤维成形中两组分入口流量比对纤维成形有直接的影响，所以通过改变熔体的入口流量比来研究熔体之间互相的影响情况，在总流量不变时，选取PA 6:PET流量比分别为2:1，1:1，1:2。从图3可以看出，两种聚合物熔体入口流量比的变化对于界面偏移影响较大。当PA 6:PET流量比为2:1时，PA 6组分与PET组分的半径变化分布很匀称。当PA 6:PET流量比为1:2时，PET组分对PA 6组分挤压非常严重。两种流体入口流量比的变化会引起共挤出界面位置和形状的变化。随着两种熔体流量差异的增大，界面位置偏移量增大。当总流量不变，随着PA 6:PET流量比的增大，纤维的L2/S减小。当PA 6:PET为1:2时，纤维的L2/S为30.2，当PA 6:PET为2:1时，纤维的L2/S为25.1，纤维的L2/S减小了16.9%。另外，复合扁平纤维的丝条温度沿纺程逐渐降低，改变流量比时，丝条温度变化不是很明显。

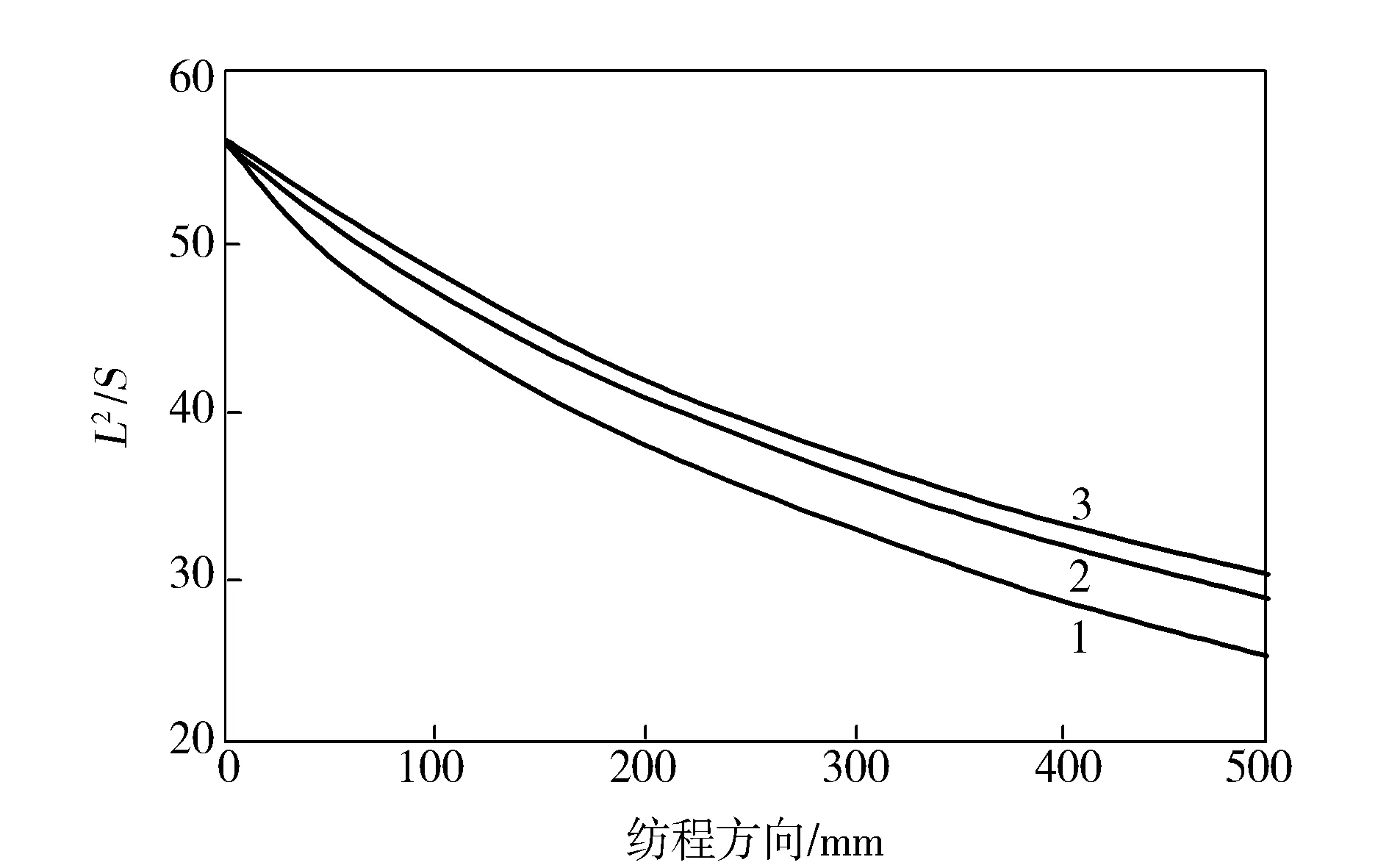
图3 不同流量比下纤维L2/S沿纺程方向的变化Fig.3 Change of L2/S of fibers along with spinning path at differnet flow ratio1—PA 6:PET流量比为2:1；2—PA 6:PET流量比为1:1；3—PA 6:PET流量比为1:2

方案二：选择PA 6流量增加(分别为1.5×10-7，2.0×10-7，2.5×10-7m3/s),PET流量不变为1.5×10-7m3/s进行模拟。由图4可知：复合扁平纤维的L2/S随着PA 6流量的增加而增大；当PA 6流量为1.5×10-7m3/s时，纤维的L2/S为28.8；当PA 6流量为2.5×10-7m3/s时，纤维的L2/S为33.6，纤维的L2/S增大了12.4%；另外，随着总流量的增加，复合纤维的丝条温度沿纺程方向降低的趋势变缓，结晶固化点的位置下移，纤维变形区间变宽。

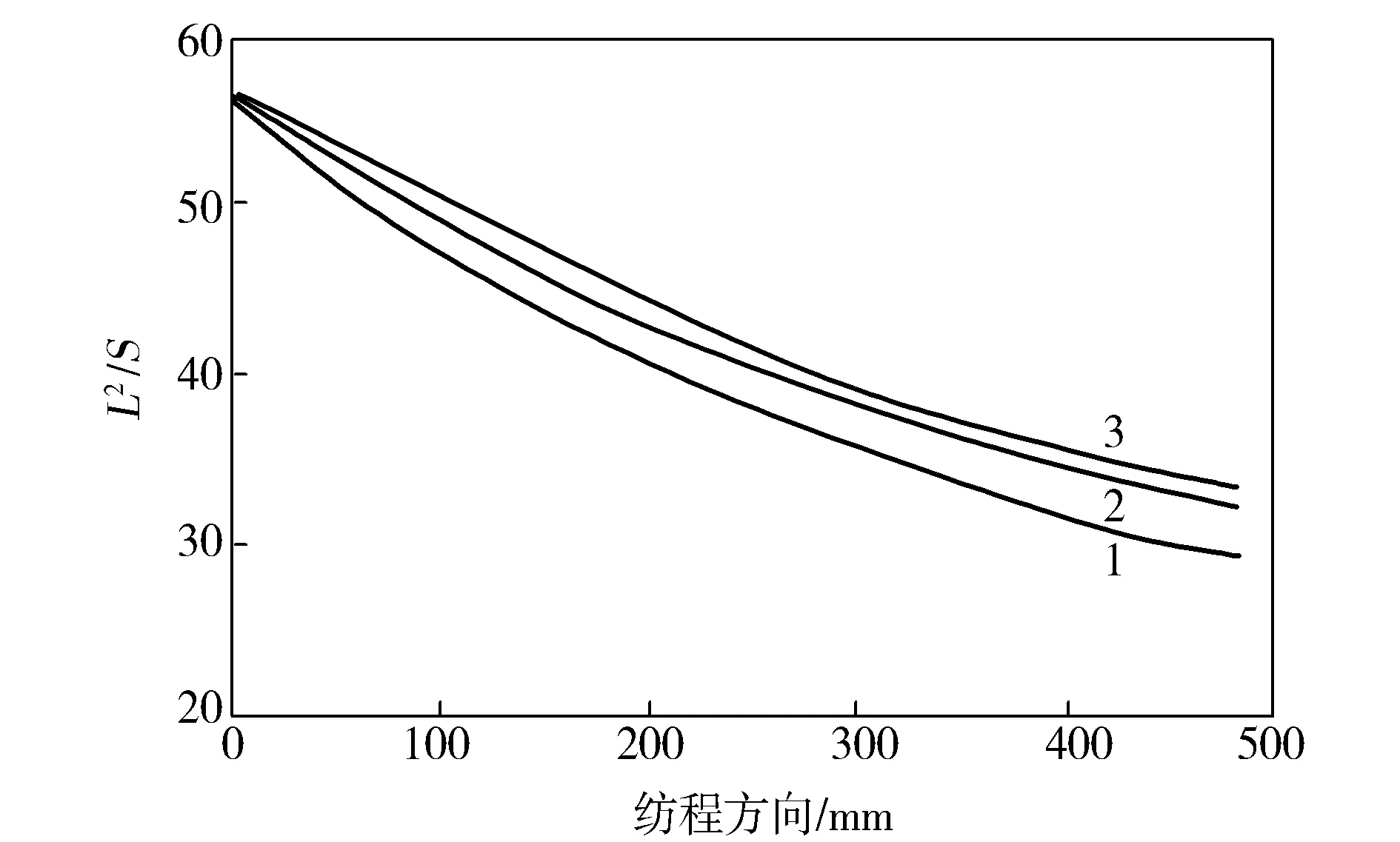
图4 不同PA 6流量下纤维L2/S沿纺程方向的变化Fig.4 Change of L2/S of fibers along with spinning path at different PA 6 flow1—PA 6流量为1.5×10-7m3/s；2—PA 6流量为2.0×10-7m3/s；3—PA 6流量为2.5×10-7m3/s

3.2 纺丝温度

复合异形纤维的L2/S对成形过程中的温度变化较为敏感，当熔体挤出速度较快时，熔体细流较快进入纤维的成形区，使丝条的黏度迅速增加，松弛时间延长，有利于L2/S的提高。由图5可看出，纤维的L2/S随着纺丝温度升高而降低，纺丝温度从282 ℃升高到287 ℃时，L2/S下降11.4%，从287 ℃升高到292 ℃时，L2/S下降4.8%。

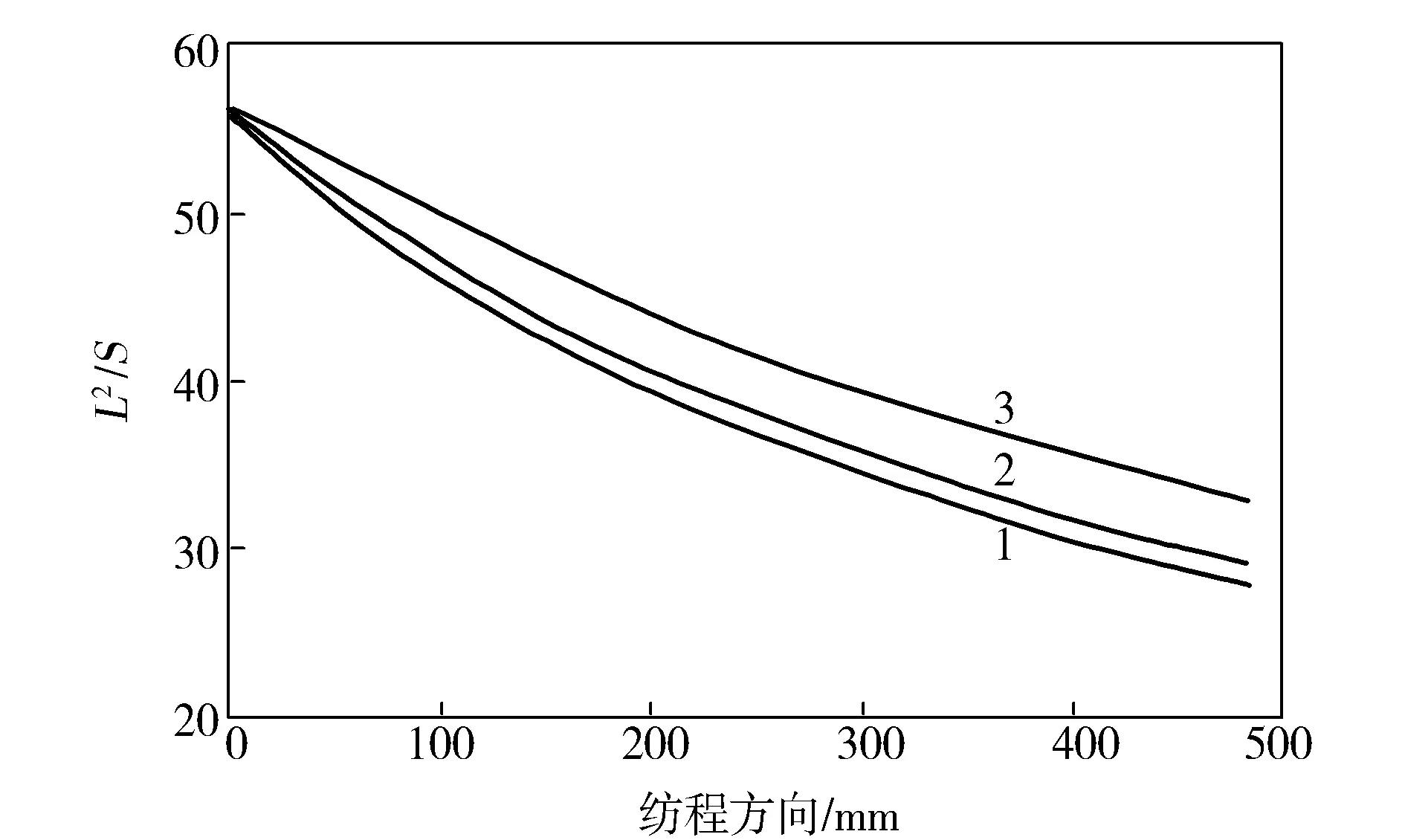
图5 不同纺丝温度下纤维L2/S沿纺程方向的变化Fig.5 Change of L2/S of fibers along with spinning path at different spinning temperature1—292 ℃；2—287 ℃；3—282 ℃

虽然熔体的松弛时间随温度的升高而下降，使熔体挤出喷丝孔后的膨化现象减少，熔体的表面张力减小；但是纺丝温度对熔体的黏度也有很大的影响，随纺丝温度的升高，熔体的黏度逐渐下降，挤出物偏离喷丝孔形状的阻力减小，研究表明纺丝温度对后者的影响要大于前者[10]。因此，纤维的L2/S随纺丝温度的升高而下降。

3.3 单组分与复合组分扁平纤维的模拟对比

由图6可以看出，PA 6/ PET复合扁平纤维的横截面形状介于单组分PA 6纤维和单组分PET纤维之间，其形状类似“钥匙”形。

图6 扁平纤维截面形状Fig.6 Cross section shape of flat fiber

从图7可以看出，熔体在刚挤出喷丝板时，由于挤出胀大的原因，纤维的L2/S急剧减小，随着熔体的恢复，L2/S慢慢有所增大，但沿纺程方向纤维的L2/S的趋势是逐渐减小。相比单组分扁平纤维，PA 6/ PET复合扁平纤维截面更不规则，PA 6/PET复合扁平纤维的L2/S大于单组分纤维的L2/S。熔体的膨化程度主要是由于两者的黏度不同起作用，若是两种不同的熔体，膨胀的程度显然会不同，则扁平纤维的“钥匙”形状也会不一样，两种组分的黏度对复合异形纤维的形状起决定性作用。

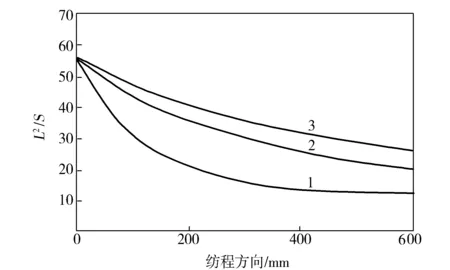
图7 不同组分纤维的L2/S沿纺程方向的变化Fig.7 Change of L2/S of fibers with different components along with spinning path1—PA 6；2—PET；3—PA 6/PET

4 结论

a. 在并列型PA 6/PET复合扁平纤维纺丝中，两种流体入口流量比的变化会引起共挤出界面位置和形状的变化。

b. 当总流量不变，随着PA 6:PET流量比值的增大，纤维的L2/S减小。当PA 6:PET流量比为1:2时，纤维的L2/S为30.2，当PA 6:PET流量比为2:1时，纤维的L2/S为25.1，纤维的L2/S减小了16.9%。

c. 复合扁平纤维的L2/S随着总流量的增加而增大，随着总流量的增加，复合纤维的丝条温度降低的趋势变缓。

d. 纤维的L2/S对成形过程中的纺丝温度变化较为敏感，复合扁平纤维的L2/S随着纺丝温度的升高而降低，纺丝温度从282 ℃升高到287 ℃时，L2/S下降11.4%，纺丝温度从287 ℃升高到292 ℃时，L2/S下降4.8%。

e. 复合纤维中两种组分的黏度对复合异形纤维的形状起决定性作用。

[1] 董纪震，罗鸿烈，王庆瑞，等．合成纤维生产工艺学[M]．2版．北京:中国纺织出版社，1991:13，168．

Dong Jizhen, Luo Honglei, Wang Qingrui, et al. Synthetic fiber production process[M]. 2nd edit. Beijing: China Textile Industry Press, 1991:13,168.

[2] 杨崇倡. 异形纤维喷丝板的设计加工及其应用研究[D]. 上海：东华大学，2008.

Yang Congchang. Study on design processing and application of spinneret for profiled fiber[D]. Shanghai: Donghua University, 2008.

[3] 纪占国. 分层界面滑移对聚合物共挤成型过程影响的数值模拟研究[D]. 南昌: 南昌大学，2008.

Ji Zhanguo. Numerical simulation research of the effect of interfacial slipping on polymer co-extrusion formation process[D]. Nanchang: Nanchang University, 2008.

[4] Aloku G O , Yuan Xuefeng. Numerical simulation of polymer foaming process in extrusion flow[ J] . Chem Eng Sci, 2010 ,65(12 ):3 749-3 761.

[5] 柳和生，涂志刚，熊洪槐．聚合物熔体在直线型异型材挤出口模内三维粘弹流动分析[J]．应用基础与工程，2004，12(1):73-79．

Liu Hesheng, Tu Zhigang, Xiong Honghuai. Numerical simulation of three dimensional viscoelastic polymer melt flow through the extrusion die with an irregular cross section composed of lined up components[J]. J Basic Sci Eng, 2004，12(1):73-79.

[6] 郭燕冲，崔毅华，王新厚．熔喷非织造衣架型模头中聚合物流动数值模拟[J]．纺织学报，2006，27(10):18-21．

Guo Yanchong, Cui Yihua, Wang Xinhou. Numerical simulation of polymer flow in the coat-hanger die of melt blown process[J]. J Text Res, 2006，27(10):18-21．

[7] 刘玉军，王钧效．衣架式纺丝模头设计理论研究[J]．纺织学报，2008，29(3):97-100．

Liu Yujun, Wang Junxiao. Theoretical study on design of coat-hanger die[J]. J Text Res, 2008，29(3) :97-100．

[8] 刘斌，马骏．Polyflow逆向挤出功能在异型材口模设计中的应用[J]．计算机辅助技术，2008，36(1) :66-70．

Liu Bin,Ma Jun.Application of polyflow inverse extrusion in the design of profile die[J].Plast Sci Tech,2008，36(1):66-70．

[9] 刘丽研，黄故，王瑞．热塑性复合材料薄板拉伸过程有限元模拟[J]．纺织学报，2007,28(11):45-47.

Liu Liyan, Huang Gu, Wang Rui. Finite elemental simulation on tensile process of thermoplastic laminates[J]. J Text Res, 2007，28(11):45-47.

[10] 周兆云，王华平，王朝生,等. 扁平纤维熔融纺丝动力学模型[J],聚酯工业,2006,19(5):1-4.

Zhou Zhaoyun, Wang Huaping, Wang Chaosheng, et al. Dynamic model of flat fiber in melt-spinning[J]. Polyest Ind, 2006,19(5):1-4.

Numerical simulation of extrusion-forming process of side-by-side PA 6/PET composite flat fiber

Ning Ning, Gan Jiajia, Feng Pei, Chen Ge

(EngineeringResearchCenterofAdvancedTextileMachineryofMinistryofEducation,DonghuaUniversity,Shanghai201620)

A model for simulating the extrusion-forming process of side-by-side polycaprolactam (PA 6)/polyethylene terephthalate (PET) composite flat fiber was established by using PA 6 and PET as raw material under different flow and spinning temperature with a Polyflow software. The change of the cross section shape coefficient and tow temperature was analyzed during the process of extrusion formation. The results showed that the variation of the flow ratio of PA 6 and PET at the inlet would result in the change of extrusion interface position and shape during composite spinning process; the shape coefficient of PA 6/PET composite flat fiber was decreased with the increase of the flow ratio of PA 6 and PET and was increased with the increase of the total flow, but the fiber temperature was decreased more and more slowly with the increase of the total flow; and the shape coefficient of the composite flat fiber was also decreased with the increase of spinning temperature.

polycaprolactam fiber; polyethylene terephthalate fiber; composite spinning; flat fiber; shape coefficient; numerical simulation

2016- 06-20； 修改稿收到日期：2016-10- 09。

宁宁(1988—)，女，硕士研究生，主要研究方向为涤锦复合异形纤维的成形工艺与装备的研发。E-mail：15026561831@163.com。

TQ342+.94

A

1001- 0041(2016)06- 0060- 05