含变容二极管电路系统的Melnikov混沌及其控制

谷 飞，方见树,2

（1. 湖南工业大学 理学院，湖南 株洲 412007；2. 湖南工业大学 物理研究所，湖南 株洲 412007）

含变容二极管电路系统的Melnikov混沌及其控制

谷 飞1，方见树1,2

（1. 湖南工业大学 理学院，湖南 株洲 412007；2. 湖南工业大学 物理研究所，湖南 株洲 412007）

以一个含变容二极管的电路系统为研究对象，分析并推导出该电路系统所满足的非线性方程。并运用直接微扰法求得该方程的微扰解，且由Melnikov混沌判据得知该微扰解是一混沌解，表明该非线性电路系统具有混沌特征。理论解析结果表明，通过调节系统参数或初始边界条件可以对系统的混沌加以控制。相应的数值仿真结果表明，所提方法确实有效可行，验证了理论解析结论。

变容二极管电路；混沌现象；Melnikov判据；控制

0 引言

混沌是指在确定性系统中出现的一种貌似无规则、类似随机的现象，是非线性系统在满足一定条件时必然出现的一种复杂运动形式。混沌运动广泛存在于湍流、各种物理振动、多体动力学系统、化学反应及生命体运动等自然现象中。混沌运动具有许多特殊的性质，如对初始条件和系统参数的微小变化极端敏感、运动的相空间轨道有界但却有着正的李雅普诺夫指数等[1-2]。自20世纪60年代产生以来，混沌理论发展非常迅速，它对现代科学产生了广泛而深远的影响，并在数学、物理学、经济学、生物医学、生态学、保密通讯及自动控制等领域得到了广泛的应用。

含有变容二极管的电路是一种典型的非线性电路[3]，电路中用到的重要原件是变容二极管，而变容二极管作为一种可调谐电抗元件，被广泛应用于自动频率控制、振荡电路、调频以及各种通信系统中。由于非线性电路系统中存在混沌现象，因而难以调控。本文拟运用直接微扰法对含变容二极管电路的系统进行理论解析，并且采用Melnikov混沌控制方法[4]对该非线性电路的混沌行为进行相应的调控。最后，通过数值模拟验证所得的理论结果，以期为相关电路系统或其它物理系统中的混沌控制提供一定的理论参考。

1 含变容二极管电路的动力学方程

图1所示为一个含有变容二极管的非线性电路，其中C1为变容二极管串联电容，变容二极管的结电容C与反向电压VC的关系如式（1）所示：

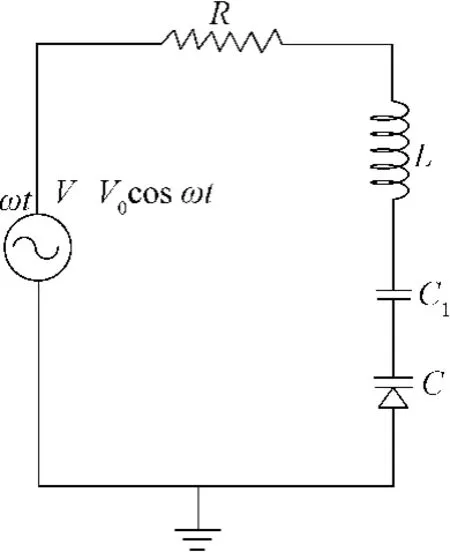
图1 变容二极管电路Fig.1 Variable capacitance diode circuit

适当调节C1/C0，以保证VC/<<1，于是可得下列近似关系[5]：

2 动力学方程的解析解

方程式（8）是含有变容二极管电路系统无量纲化后的动力学方程，它是一典型的非线性方程。现利用定量的解析方法即周期微扰法，讨论该非线性电路系统的混沌行为[7-9]。为了简便，将式（7）写成如下形式：

3 数值模拟结果

上文利用解析的方法得到了含有变容二极管电路系统的混沌解，这从理论上表明该非线性电路系统具有混沌行为。为了印证这一理论结果，下面采用数值仿真手段模拟该系统的混沌行为。在方程（9）中，选定参数，运用计算软件Mathematica得到的数值仿真结果见图2。

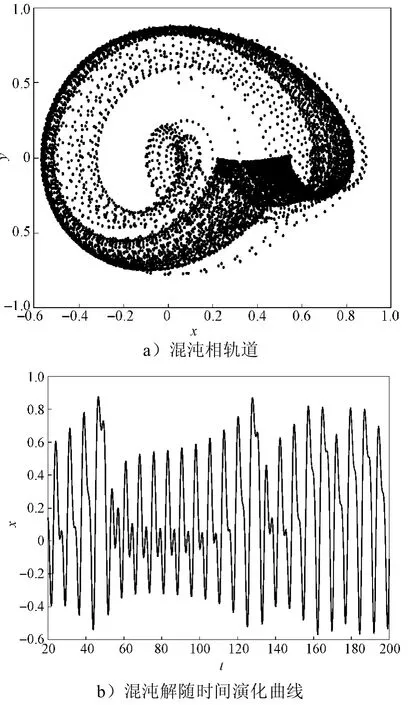
图2 系统在=0.2,=0.51,=1.7,=0参数条件下的混沌图像Fig.2 Chaotic image under conditions of=0.2,=0.51,=1.7,=0

图2 a为系统的相轨道，可看出其变化非常复杂，而且含有混沌吸引子，此结果表明该含变容二极管电路系统确实存在混沌行为，从而印证了前文的理论解析结果。

图2 b所示为非线性方程（9）的解x随时间变化的图像。从该图可看出，系统随时间的演化曲线是极其复杂的非周期曲线，没有规律可循，这也体现了该非线性系统的混沌特征，与前面的理论解析结果一致。但该非线性电路系统的混沌可以通过调节系统参数或改变系统的初、边界条件加以控制。例如，通过在方程（9）和（10）中对参数和进行调节，即可对系统的混沌进行控制，让混沌轨道变成周期轨道。如果将系统参数设定为0.488，将参数设定为2.2，其他参数与图2中的相同，则可得到如图3所示的数值模拟结果。

图3 系统在=0.2,=0.488,=2.2参数条件下的4周期相图Fig.3 Four periodic phase diagram of the system underconditions of=0.2,=0.488,=2.2

从图3a中可看到，系统的相轨道是由4个单周的轨道复合而成的4周期轨道，这表明系统从混沌态进入了准周期态，系统混沌得到了部分控制。从图3b所示4周期解与时间的变化关系曲线可看出，其系统状态参数的变化是有规律可循的，呈周期态变化。

图4 系统在=0.2,=0.4,=2.2参数条件下的双周期相图Fig.4 Double periodic phase diagram of the system underconditions of=0.2,=0.4,=2.2

图5 系统在=0.2,=0.38,=2.2参数条件下的单周期相图Fig. 5 Single periodic phase diagram of the system under conditions of=0.2,=0.38,=2.2

由图4a可以看到，在此条件下，系统的相轨道由2个周期轨道复合而成，即为双周期相轨道图像。而图5 a则是一个纯周期的相轨道，表明此时系统已由混沌态完全进入了纯周期状态，即该系统的混沌被完全控制。而相应的系统解x随时间t的演化曲线也从图2b所示的混沌曲线逐渐演化成图3b、4b和5b所示的准周期曲线和纯周期曲线。因此，结合上面的分析可以得出如下结论：通过对非线性电路系统的参数进行调节，可以对其内部的混沌行为进行有效控制。由此可见，系统参数在控制非线性电路系统的混沌中有着非常重要的作用。

图6 =0.1, 0<<2.5时系统的混沌区域图像Fig.6 Chaotic region diagram under conditions of=0.1, 0<<2.5

从图6中可看到，混沌区域在轨线的上方，下方是周期运动的区域，而且混沌区域随频率值的变化而变化。若要让系统处于周期运动状态，则应尽可能减小的数值而增大的数值。反之，系统则可能进入混沌状态。这一结论再次证明了系统参数在混沌抑制方面所起到的重要作用。

4 结语

本文采用解析和数值计算的方法，研究了含变容二极管非线性电路系统的混沌行为。首先，采用直接微扰方法得到了该非线性电路系统的微扰解，理论分析表明此微扰解是无界的；其次，由Melnikov混沌判据证明该微扰解是一个混沌解，也就是说这个含变容二极管非线性电路系统具有混沌的特征；最后，由相应的数值模拟结果印证了理论解析结果。由于混沌对系统参数、初始条件和边界条件的敏感性，可以通过调节系统参数或改变初、边界条件来控制含变容二极管非线性电路系统的混沌行为，即使系统从混沌态进入周期态。数值模拟的结果表明，该方法确实有效可行，并且这种控制混沌的方法在其他物理系统中也可以得到很好的应用。

[1]张晓丹，崔丽娟. 一类四维超混沌系统的界及同步的研究[J]. 物理学报，2011，60(11)：151-157. ZHANG Xiaodan, CUI Lijuan. The Bound for a Class of Four-Dimensional Hyperchaotic System and Its Synchronization[J]. Acta Physica Sinica，2011，60(11)：151-157.

[2]吴然超，郭玉祥. 含一个非线性项混沌系统的线性控制及反控制[J]. 物理学报，2010，59(8)：5293-5298. WU Ranchao，GUO Yuxiang. Linear Control and Anti-Control of Chaotic Systems with Only One Nonlinear Term [J]. Acta Physica Sinica，2010，59(8)：5293-5298.

[3]刘秉正. 非线性动力学与混沌基础[M]. 长春：东北师范大学出版社，1994：152-153. LIU Bingzheng. Nonlinear Dynamics and Chaos Elements [M]. Changchun：Northeast Normal University Press，1994：152-153.

[4]雷佑铭. 典型非自治混沌系统的控制与随机控制及同步[D]. 西安：西北工业大学, 2006：14-40．LEI Youming. Research on Control, Stochastic Control, Synchronization and Noise-Induced Synchronization of Nonautonomous Chaotic Systems[D].Xi’an：Northwestern Polytechnical University Press，2006：14-40．

[5]倪皖荪，魏荣爵. 含二次非线性项受迫振动系统中的分岔与混沌现象[J]. 物理学报，1985，34(4)：503-511. NI Wansun，WEI Rongjue. Bifurcation and Chaos in Forced Vibration Systems Containing A Square Nonlinear Term[J]. Acta Physica Sinica，1985，34(4)：503-511.

[6]徐玉秀，胡海岩，闻邦椿. 杜芬方程的1/3纯亚谐解及过渡过程的分形特征研究[J]. 应用数学和力学，2006，27 (9)： 1023-1028. XU Yuxiu，HU Haiyan，WEN Bangchun. A 1/3 Pure Sub-Harmonic Solutions of the Fractal Characteristic of Transient Process for Duffing’s Equation[J]. Applied Mathematics and Mechanics，2006， 27(9)： 1023-1028.

[7]FANG Jianshu，LIAO Xiangping. Stability of Trapped Bose Einstein Condensates in One-Dimensional Tilted Optical Lattice Potential[J]. Chinese Physics B，2011，20(4)：80-84 .

[8]HAI Wenhua，ZHANG Zelan, FANG Jianshu. Chaotic Solitons in Sine-Gordon System[J]. The European Physical Journal B，2001，21(1)：103-107.

[9]FANG Jianshu. Nonlinear Transport of Bose-Einstein Condensates in a Double Barrier Potential[J]. Chinese Physics B，2008，11：3996-4001.

[10]袁文俊，阴晓玲. L’Hospital法则和Stolz定理的推广与应用[J]. 广州大学学报（综合版），2001，15(2)：18-21. YUAN Wenjun，YIN Xiaoling. The Extending Results and Applications of L’Hospital Criteria and Stolz Theorem[J]. Journal of Guangzhou University，2001(2)：18-21.

[11]SHI Linsong，ZOU Yongkui，KPPER Tassilo. Melnikov Method and Detection of Chaos for Non-Smooth Systems [J]. Acta Mathematicae Applicatae Sinica(English Series)，2013，29(4)：881-896.

（责任编辑：廖友媛）

Melnikov Chaos and Its Control in a Varactor Diode Circuit System

GU Fei1，FANG Jianshu1,2
（1. School of Science，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. Institute of Physics，Hunan University of Technology，Zhuzhou Hunan 412007，China）

The nonlinear equation of the electric power system can be deduced from an analysis of the experimental results of a research conducted on a certain varactor diode circuit system. The perturbation solution of the equations can be worked out by using the direct perturbation method. According to Melnikov chaos criteria, the perturbation solution thus obtained proves to be a chaotic solution, which shows the chaotic characteristics of the nonlinear circuit system. Theoretical analysis results show that an effective control over the chaotic behaviors in the system can be realized by adjusting the system parameters or initial boundary conditions. The corresponding numerical simulation results show that the proposed method is effective and feasible, thus verifying the results of the theoretical analysis.

varactor diode circuit；chaos phenomena；Melnikov criteria；control

O415.5

A

1673-9833(2016)05-0081-06

10.3969/j.issn.1673-9833.2016.05.016

2016-08-24

谷 飞（1993-），男，安徽马鞍山人，湖南工业大学硕士生，主要研究方向为复杂电路网络系统及其控制，E-mail：964031019@qq.com

方见树（1956-），男，湖南益阳人，湖南工业大学教授，主要从事凝聚态物理中的非线性问题，非线性动力学与混沌等方面的研究，E-mail：fjs289@163.com