论如何提高初中学生的数学解题能力
杨晓兰
(官渡区金马中学 云南昆明 650216)
论如何提高初中学生的数学解题能力
杨晓兰
(官渡区金马中学 云南昆明 650216)
不少学生反映,课上听得懂,就是自己不会做;即使把定理背的滚瓜烂熟,把公式默写的一字不差,也模仿例题做了不少练习,可课下一解题,经常出错,而遇到新题又束手无策。究其根源:教学!“教”:照本宣科,学生依样画葫芦;“学”:学习者不求甚解,不去深入的领悟所学知识,更不重视探索过程、发现过程的反思,只求知道个最终结论或最终套路。我为了提高学生的数学解题能力,在教学中留心多年,先将点滴体会介绍如下,仅供参考。
一、新课讲授准确、全面,并据前瞻性
例如,在讲授(人教版第二十四章)圆和圆的位置关系一单元时,若采用:通过板演圆与圆五种位置关系的图形,引导学生观察并发现五个等价命题之后,便开始例题教学,布置学生完成书后练习与习题,表面上看一帆风顺,实质由于教师的照本宣科,学生失去了一次深入理解,发展提高的机会。所以在教学中,我除了先幻灯演示,然后板演书上五种位置关系外,还让学生在我的提示下观察图①,发现:同在x轴上的两个半径分别为R.和r(R>r)的⊙A和⊙B,圆心A、B的坐标分别是(xA,0)和(xB,0),则圆心距d=│xA-xB│。外切时,圆心距d=│xA-xB│=R+r;内切时,圆心距d=│xA-xB│=R-r;内含时d=│xA-xB│<R-r,等。
还有,两个圆相交,除黑板上、书上所画的两个圆的圆心分别在公共弦两侧这种情况外,圆心还有别的情况吗?结果,学生通过思考,作图后发现,原来两圆相交,还有圆心在公共弦同一侧的情况。接着又进一步提出:这两种情况中圆心距、半径、弦心距三者关系有什么不同吗?对照观察图②、图③后,学生发现:当圆心在公共弦两侧时,两圆圆心距等于弦心距(这里指公共弦的弦心距)之和;而当两圆圆心在公共弦同一侧的时侯,圆心距则等于弦心距之差。如果讲完课,未做适当引申与拓展,一旦新题型出现,学生肯定:要么,束手无策;要么解错了。

图1

图2
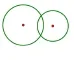
图3

图4
例如:2010.聊城中考就有这样一道题:如图④,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0),半径为5,如果两圆内含,那么a的取值范围是_。一些同学无从下手,而另一些同学又会错误的答成0<a<2;而正确的解答是:因为内含,所以圆心距“│a│”必小于半径之差,即∵│a│<2,∴-2<a<2;
再如,由于学生对两圆相交缺乏全面认识而导致错误的题:相交两圆的公共弦为6,两圆的半径分别为和5,则这两圆的圆心距为_。很多学生因为对两圆相交考虑不全面,只答出了7,而漏答了1。
以上两例充分说明,学生解题能力与教学的关系了。若教学中,充分意识到知识的引申与拓展的必要性的话,情况会大不一样!多年教学尝试与思索中我深深悟到:学生解题能力差,往往是教师教学启发的不够,前瞻性不强所致,教学中应多一分思索、多一点启发,学生将会越来越爱学、越来越会学,也越来越聪明。
二、一题多解、甚至巧解,且充分重视对探索过程、发现过程的反思
例如,再讲2010.乐山中考一题:如图⑤,正六边形ABCDEF的边长为2cm,点P为这个正六边形内部的一个动点,则点P到这个正六边形各边的距离之和为__cm。有学生把P点当作正多边形的中心后,迅速得出结果理由是此时距离之和应是边心距的6倍。首先肯定,这样做很巧妙,答案也固然对,但至于为什么便不去想它了。
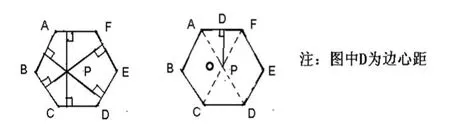
图5
此时,因不失时机引导学生去探索、去发现:①通过六个三角形面积之和等于总面积而得出;②由正六边形三组边分别平行,而平行线之间的距离处处相等,从而推出:点P到这个正六边形各边的距离之和是个定值,为边心距的六倍。接着问:如果改为是正三角形、正五边形、正七边形,……,其他条件不变,结论又会如何呢?为什么?你能得出个公式来吗?学生在一个个问题的层层深入中去思考、去讨论、去发现,最后得出结论:通过n个三角形面积之和等于正n边形的总面积,可得出一个公式:正n边形内任意一点到各边的距离之和一定是此n边形边心距的n倍。以上教学,不但解决这道题,还让学生学会了利用面积比拼解决其它多边形中这类问题的方法,更重要的是通过引导学生在思考、探索中不断发现,不断去总结,既提高了学生的数学思想,又培养了学生的钻研精神和严谨科学态度。长此以往,学生的数学解题能力才能得以真正意义上的提高。
再比如,初三第二十二章 22.3实际问题与一元二次方程教学过程中遇到的利用平移方法解决面积问题的教学中,我做了这样的尝试:
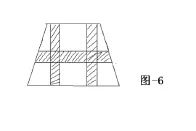
例如,(人教版P54页)这样一道题:如图⑥,要设计一个等腰梯形的花坛,花坛上底长100,下底长180,上下底相距80,在两腰中点连线处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等,用到的面积是梯形面积的六分之一,甬道的宽应是多少米?(结果保留小数点后两位)
学生因为有教材P49页第9题以及一些变式训练,如


于是迅速找到突破口,有了下列解法:
解:设道路的宽度为x米
学生分别有两种列法:

其中第二种方法显然运用了平移的数学思想,但必须提出让学生思考的是:当我们把横着的道路去除后,上下两个梯形已不能组成一个高减小x米的梯形了,为什么你们还能用平移拼接的方法列出了第二种形式的方程呢?难道错了吗?如果对,那又是为什么呢?为讲清楚这个问题,我把图形研究的重点放在如何裁剪中间甬道后,再拼接的问题作为重点。让学生用动脑、也动手,逐渐明朗、发现:
此题中最重要的一个条件:“在两腰中点连线处有一条横向甬道”,也正因如此,如图,
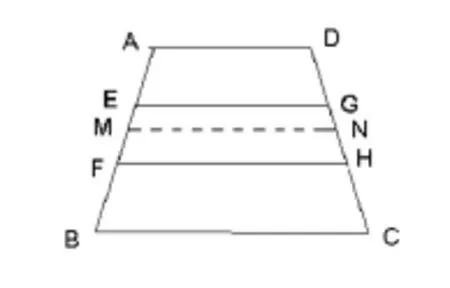
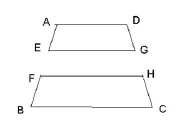
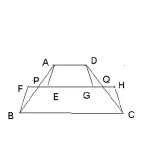

所以,第二种采用平移、比拼方式列的方程也就是正确的了。
通过以上分析与反思,使学生知其然,也知其所以然了。
三、上好复习课,要合理设置有针对性和代表性的例题和练习题。例如,在组织学生复习一元二次方程解法时,我先从一元二次方程的概念入手,配备例题,以便更好的帮助学生理解并掌握
再如,在学完反比例函数之后,我及时上了堂复习课,复习中除了对反比例函数图像、性质、典型体例做复习外,我还把它和一次函数(包括正比例函数)又做了对比,复习中既注意它们的区别,更加强了由易到难、分层次、阶梯式的综合训练,这样,我认为不单单提高了学生的解题能力,更重要的是培养学生学好数学的方法和习惯,既提高了学生智力,又注重了学生非智力因素的培养。下面是我设计的一组题:
2.已知一次函数与反比例函数的图像交于点p(-2,1)和Q(1,m)。求这两个函数的解析式,在同一坐标系内画出图像,并根据图像回答:当x为何值时,一次函数的值大于反比例函数的值。(此题既巩固了函数的基本知识,又训练了学生运用数形结合的方法来解答问题的能力)。
3.为了与预防流感,某学校在休息天用药物消毒法对教室进行消毒。已知药物释放过程中每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系是为为常数),如图所示。据图中提供的信息,解答下列问题:
①写出从药物释放开始,y与t的两个函数关系式及相应的自变量取值范围;

②据测定,当空气中每立方米的含量降低到0.25毫克时,考生方可进入教室,那么从药物释放开始,至少需要多少小时后,考生才能进入教室?(既巩固了知识,提高解题了能力,更重要的是,对学生数学学以致用能力的提高进行了很好的训练)。
综上所述,教学中也只有通过比较、探索、讨论、反思,甚至是争论的过程,学生才能真正弄懂,并从根本上理解和体会数学的乐趣,不自觉的在每一次体验中提高数学的解题能力,更长远一点说:为学生的后继学习和可持续发展打下来良好的基础。因此,我认为在教学中:不能只求学生一时的懂,而要为教学生为求精而学!

