复杂快中子源编码成像高效模拟方法研究

张凤娜,张天奎,王东明,郑向阳,胡华四

(1.西安交通大学能源与动力工程学院,710049,西安;2.中国工程物理研究院激光聚变研究中心,621900,四川绵阳;3.环境保护部核与辐射安全中心,100082,北京)



复杂快中子源编码成像高效模拟方法研究

张凤娜1,张天奎2,王东明1,郑向阳3,胡华四1

(1.西安交通大学能源与动力工程学院,710049,西安;2.中国工程物理研究院激光聚变研究中心,621900,四川绵阳;3.环境保护部核与辐射安全中心,100082,北京)

为了解决快中子编码成像中复杂源图像定义与模拟效率的问题,研究了基于深度优先合并方法的复杂源图像定义方法。采用栅元合并技术来减小源定义所需栅元数目,同时保证蒙特卡洛模拟中源抽样的效率,从而提高复杂源图像编码成像模拟效率。模拟源为二值E字母时,源合并后模拟所得编码像的计算结果最小误差较源合并前没有变化且满足统计要求,计算时间则减少且为源合并前模拟时间的1/5;对16、64和256灰度阶E字母源进行了编码像的模拟计算,模拟结果的最小误差小于1%,符合重建研究的需要;采用3种重建算法对“西安交通大学校徽”复杂二值源的定义和模拟进行了源区重建,进而验证了基于深度优先合并的源定义方法的正确性。该方法可望为增进聚变源区所历复杂过程诊断的适应性提供一种切实可行的技术途径。

快中子编码成像;深度优先合并;复杂灰度源;蒙特卡洛模拟;图像重建

核聚变产物主要包括中子和α粒子、质子等带电粒子及光子。聚变热核反应区的形状反映了驱动的对称性、流体力学的不稳定性及辐射的烧蚀等许多物理因素,是判断点火成功与否的关键物理参量[1]。与X射线成像相比,聚变反应产生的粒子可以更直接地反映聚变等离子区域的形状和热核反应的燃烧对称性。产生于聚变高密度等离子体区域的快中子平均能量在14.1 MeV,其具有很高的穿透能力,可以从聚变压缩区域穿出,因此采用以快中子为对象的编码成像技术,通过对源区进行编码成像,由编码图像经重建可获得源图像,这种重建源图像可以清晰地反映聚变压缩区域的尺寸、形状和均一性等特征[2-5]。实验研究表明,聚变的压缩区域形状和分布具有非对称、非规则的特点,反映在源图像(表征中子发射分布)上则呈现为多灰度阶的复杂形状分布[6]。然而,编码过程模拟中多灰度阶复杂源的建模和模拟过程效率较低,因此复杂源图像研究需要发展高效的建模技术。

建立复杂形状灰度源图像的编码模拟方法,对中子成像系统参数设计与重建算法研究具有重要意义[7]。重建算法建立的目的在于对聚变等离子区域进行诊断,以反映真实的聚变物理过程。等离子区域的形状和中子强度分布是聚变物理过程中十分重要的信息,这要求重建算法的重建结果必须能够很好地反映这些信息,其中中子强度分布反映在重建源图像上就是像素点的灰度值。因此,成像模拟的难点就在于需要实现复杂形状且灰度值很高的源图像模拟。MCNP是美国Los Alamos国家实验室应用理论物理部的Monte Carlo小组研制的蒙特卡洛程序。目前,MCNP中的复杂形状面源是采用很薄的体源实现的,图像像素点灰度值表示体源的厚度,灰度越高,厚度越大,相同面积(每个像素点是大小相同的正方形)下中子抽样也就更多,这符合高像素灰度、高中子发射强度的对应关系。在MCNP输入卡片中,如果要实现复杂形状二值源图像或灰度阶数很高的灰度源图像的模拟,则源栅元的定义就需要很多个基本单元体(一般采用六面体)进行叠加,这一方面导致栅元定义语句很长,超过MCNP栅元定义语句1 000个字(word)的长度限制,另一方面栅元定义的分散性使得模拟计算的效率很低。

为了解决复杂源图像定义与模拟效率的问题,本文研究了基于深度优先合并方法的复杂源图像定义技术。通过栅元合并技术,减小源定义所需栅元数,同时保证蒙特卡洛模拟中源抽样的效率,从而提高复杂源图像编码成像模拟的效率。

1 中子编码成像系统模型

聚变快中子编码成像模拟是采用MCNP[8-9]模拟实现的。MCNP主要应用于复杂三维几何结构中粒子输运的计算,可模拟光子、中子、中子-光子耦合及光子-电子耦合等的输运问题。中子编码成像系统模型见图1,模拟所用源为氘氚(DT)聚变中子,峰值能量为14.1 MeV,源区视场直径为10 mm。成像系统的放大倍数为5,编码孔采用60 mm长的钨孔[10-12],图像探测器采用塑料闪烁光纤BCF-10组成的阵列[13],长度为100 mm,排布为199×199,单根光纤的直径为500 μm。在模拟中,整个成像系统置于空气环境中。图像探测器在闪烁光纤阵列的光纤芯部,用其记录中子在闪烁光纤阵列中的能量沉积。经过上述模型模拟获得的编码图像考虑了源区快中子经过编码孔的编码效应,也考虑了中子与闪烁光纤的作用过程。

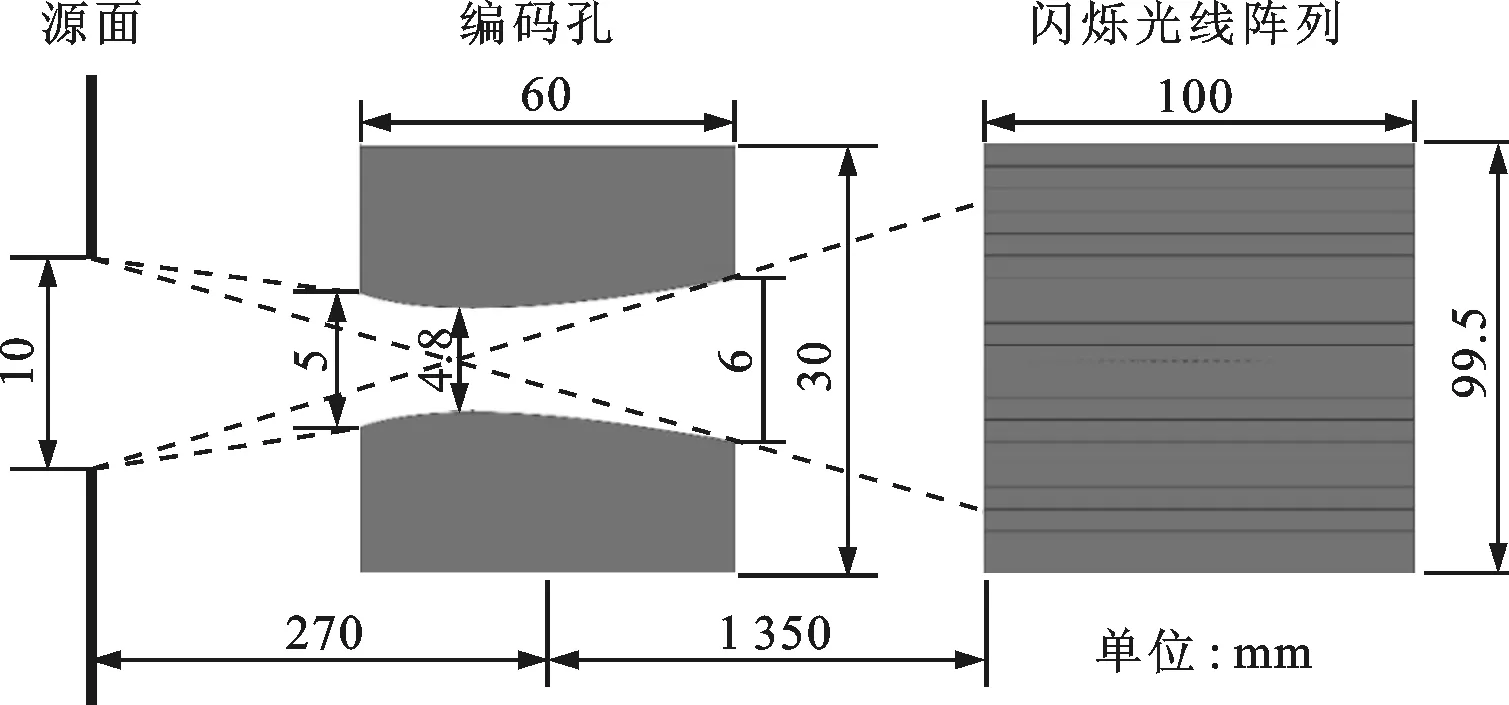
图1 中子编码成像系统模型

中子编码成像中普遍采用2种MCNP编码成像模型:基于重复结构的能量沉积模型[14-16];基于FIR(flux image radiograph)的点通量探测模型[16-17]。采用能量沉积计数的优点是模拟过程比较全面,但是效率很低;采用FIR计数,由于不需要闪烁光纤阵列作为计数器,因此计算效率高,但无法计算到达像面的中子在闪烁光纤阵列中能量沉积的过程。在本编码成像系统中,虽然中子与闪烁光纤阵列材料作用过程中的串扰等因素[18]也会对编码图像造成一定的影响,但是总体而言孔的编码是主要的编码过程,所以FIR计数器获得的编码图像可以很好地反映真实的编码图像,尤其是可以计算不同编码孔材料的散射效应和透射效应[16]。本文旨在研究复杂源图像的模拟方法,因此为保证计算效率,模拟中采用FIR点通量探测模拟模型。

2 复杂源图像定义方法

首先通过对MCNP的修改与重编译,使栅元定义长度由1 000个字长增加为100 000个字长,这样对应源定义的栅元可以包含的六面体数便由64个增加为7 692个,能满足像素数为100×100源面的定义需要。在此基础上,为提高计算效率,参考医学领域的体元合并算法[19],开展了源定义的栅元内六面体的合并研究。

2.1 源栅元六面体合并的基本定义

源栅元定义中六面体合并的算法,是将灰度值作为特征值,合并相同特征值(特征值大于0)的六面体,减少源定义栅元的六面体数目,从而提升MCNP模拟的效率。

为了实现源定义的六面体与源图像的像素对应关系,给出三对坐标(系)的数学定义。

定义1 六面体所属的空间坐标系与像素所属的平面坐标系。

空间坐标系见图2a,其中y轴方向的尺寸与源图像像素点的灰度值成正比,而六面体合并的特征值为源图像的灰度值。另外,面源定义由体源代替,所以在y方向并无六面体的多层分布。因此,空间上六面体的合并可简化为面源图像上以灰度值为特征值的像素点合并。像素平面坐标系见图2b,其中y轴垂直纸面向里,为了方便调用像素点,定义i-j坐标系,取(1,1)在图像左上角,并设源图像的像素点数为N×N。

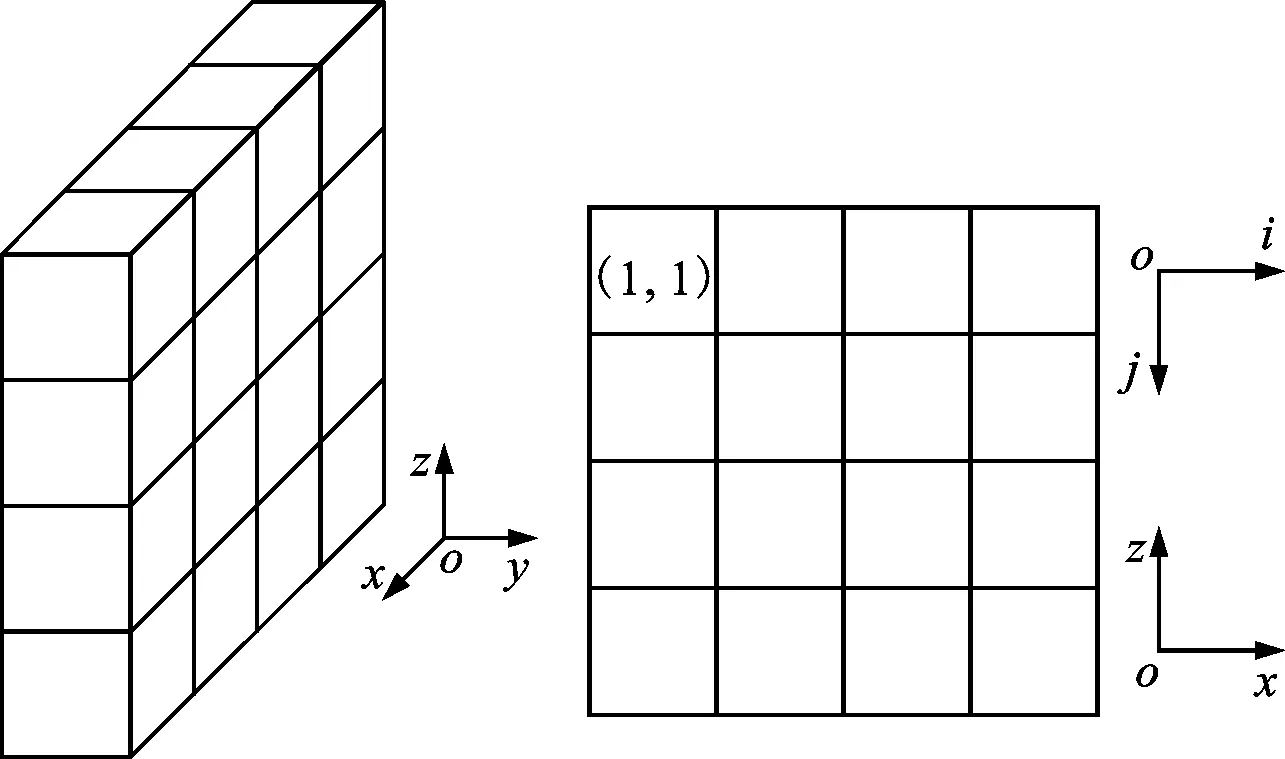
(a)空间坐标系 (b)平面坐标系 图2 六面体和像素所属坐标系

定义2 六面体坐标与像素点坐标。

结合图2,六面体中心在空间的坐标简称为六面体中心坐标(x,y,z),像素点在二维图像中的位置为像素点的坐标(i,j)。由于像素点的灰度值g(i,j)与六面体y方向的尺寸成正比,所以两组坐标的转换关系见式(1)和式(2)。

当源图像单边的像素数N为奇数时有

(1)

式中:Δs为六面体在x、z方向上划分的最小单元尺寸(μm);k为像素点的灰度值与六面体在y方向尺寸的转换比例尺寸(μm)。

当N为偶数时有

(2)

为了与模拟尺度相对应,式(1)和式(2)的常数取值为Δs=100 μm,k=0.01 μm。取k值很小的目的在于,即使像素点的灰度值g(i,j)很大,也能保证y较小,可以满足体源代替面源模拟的要求。

定义3 像素合并区域坐标与对应的六面体合并区域坐标。

将像素合并区域(长方形形状)对角线上的2个顶点的像素坐标称作该合并区域的坐标(i1,j1,i2,j2),其中i1j2,在该区域中像素点的灰度值相同,均为g(i1,j1)。采用式(3)、式(4)的坐标变换,在MCNP中定义的六面体合并区域的坐标为(x1,y1,z1,x2,y2,z2)。

当源图像单边的像素数N为奇数时有

(3)

当N为偶数时有

(4)

比较式(1)和式(3)及式(2)和式(4),式(1)与式(3)是定义了六面体中心一点,而式(2)与式(4)则需要定义合并后整个六面体的边界。

为了实现对源图像的特征值(灰度值)合并,予以下述2个合并性质进行说明。

性质1 对于像素合并区域(i1,j1,i2,j2),若i1=1(i2=N),则该像素合并区域在i负(正)方向上不可合并,对应于六面体合并区域(x1,y1,z1,x2,y2,z2)在x负(正)方向上不可合并;若j1=N(j2=1),则该像素合并区域在j正(负)方向上不可合并,对应于六面体合并区域(x1,y1,z1,x2,y2,z2)在z负(正)方向上不可合并。

性质2 设要合并区域的特征值为g(1),则对于像素合并区域(i1,j1,i2,j2),i1>1,i21。如果存在j2≤j≤j1,i=i2+1(i=i1-1),使得g(i,j)≠g(1),则像素合并区域(i1,j1,i2,j2)在i正(负)方向上不可合并,对应于六面体合并区域(x1,y1,z1,x2,y2,z2)在x正(负)方向上不可合并;如果存在i1≤i≤i2,j=j1+1(j=j2-1),使得g(i,j)≠g(1),则像素合并区域(i1,j1,i2,j2)在j正(负)方向上不可合并,对应于六面体合并区域(x1,y1,z1,x2,y2,z2)在z负(正)方向上不可合并。

2.2 基于深度优先合并的源定义方法

在以上定义和性质的基础上,深度优先的源定义方法是在像素区域合并基础上展开的,并转换成合并的六面体区域参数,从而生成MCNP的输入卡片。深度优先像素区域合并是每次选择可合并像素点行(或列)最大的方向为合并方向,流程见图3。深度优先合并算法的具体步骤如下:

(1)从像素合并区域(1,1)开始找到第一个特征值(灰度值)为g值(大于0)的像素点,以该像素点为初始的像素合并区域;

(2)根据性质1、性质2判断当前像素合并区域4个方向的可合并性,置相应的标志(真或假);

(3)判断每个可合并性为真方向上的可合并层数,合并最大层数的方向,特别当i,j方向最大可合并层数相同时,优先合并i方向,上转步骤(2);

(4)当4个方向可合并性均为假时,本次合并结束。由式(3)与式(4)将像素合并区域(i1,j1,i2,j2)变换为六面体合并区域(x1,y1,z1,x2,y2,z2),并在MCNP输入文件中写入成MCNP六面体定义语句;

(5)按顺序搜索下一个g值像素点,成功转步骤(2),否则算法结束。

上述算法完成了整个源图像上特征值为g值的像素点合并,其他每个特征值依照上述算法合并一轮,就可以完成整个源图像上所有大于零灰度值的像素点合并定义,从而实现任意形状灰度源图像定义。为了减少计算时间,模拟模型选用基于FIR点通量模型。

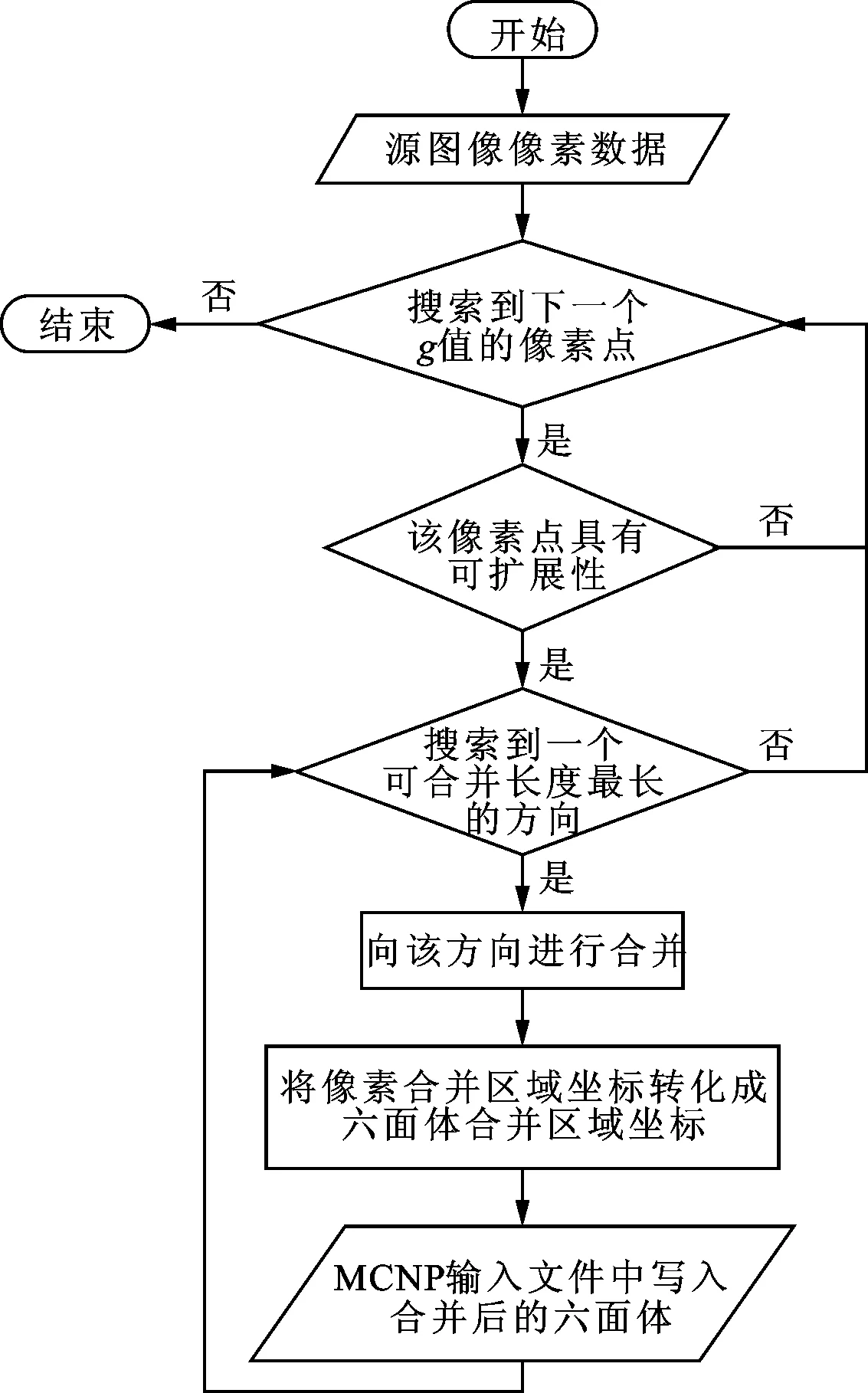
图3 深度优先合并算法流程图

在线度为1.5 mm的E字母源(见图4a)中,有信息的像素点(即属于发射中子区域的)数为89,所以在进行合并前需要定义89个六面体并组合为一个栅元作为源区域,而合并后只需要4个六面体,如图4b所示的合并区域,这样源定义所需的六面体数大大下降。同时,合并前模拟结果(见图4c)与合并后模拟结果(见图4d)一致。

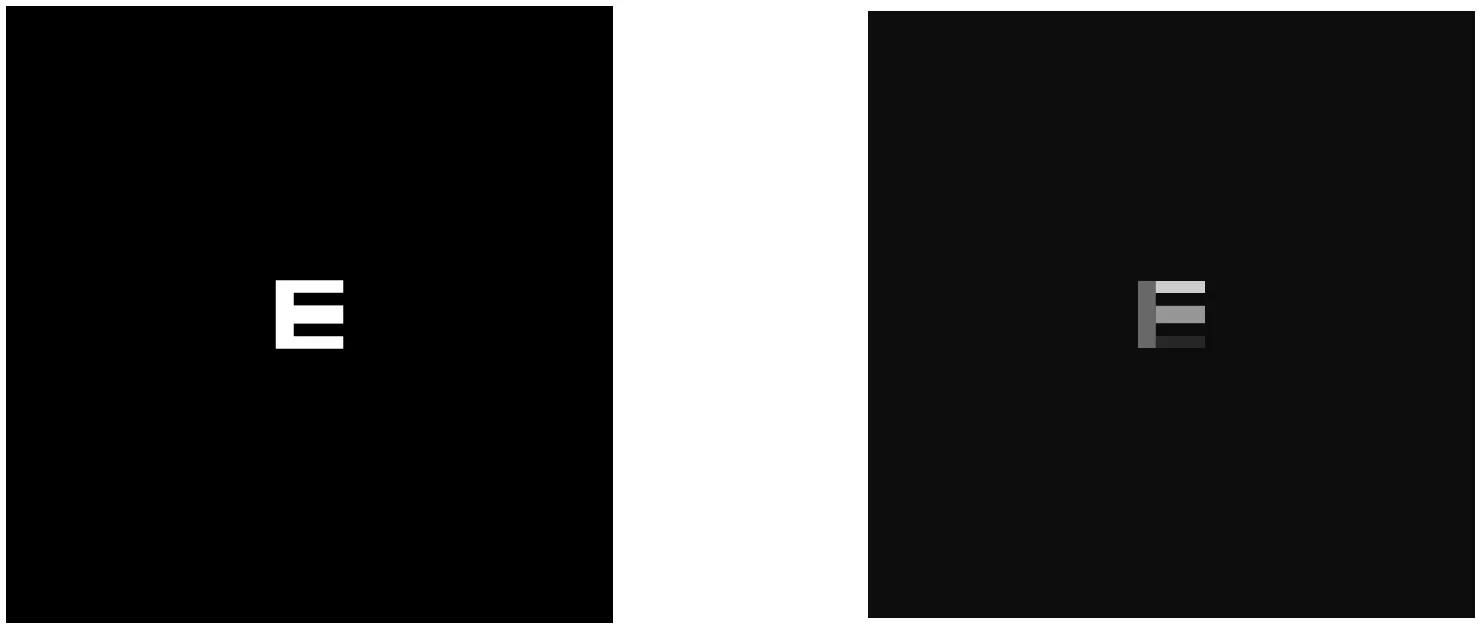
(a)源图像 (b)合并示意

(c)合并前模拟结果 (d)合并后模拟结果 图4 线度为1.5 mm时E字母源图像、合并示意与模拟结果

E字母源模拟的参数和结果见表1。采用深度优先合并后,计算结果最小误差没有变化且满足统计要求,计算时间则减少为不到合并前直接模拟时间的1/5,这说明深度优先合并方法能够大大降低模拟计算时间。

表1 线度为1.5 mm的E字母源图像合并前后模拟参数和结果

3 复杂二值源的模拟图像与重建结果

以“西安交通大学校徽”为源,通过深度优先合并定义,模拟得到其编码图像,见图5。校徽源模拟的相关参数和结果见表2。从计算结果的最小误差可以看到,模拟结果的涨落较小,也可从图5b图像很平滑得到验证。此外,从计算时间看,尽管深度优先合并的效果使得源栅元定义所需的六面体数降低到原始的1/12,但与图4所示简单二值源相比,模拟复杂形状二值源仍需大量的计算时间。

(a)源图像 (b)编码图像图5 线度为10 mm的“西安交通大学校徽”模拟结果

表2 线度为10 mm的“西安交通大学校徽”源图像模拟参数及结果

(5)

从图6的重建图像与表3重建结果的相关系数可以看出,RL算法与遗传算法的重建结果均与源图像吻合较好,从而验证了基于深度优先合并的源定义方法的正确性。因为只有在模拟正确的基础上,才能对校徽这样的复杂形状完成重建。

(a)源图像 (b)RL算法

(c)维纳滤波 (d)遗传算法图6 线度10 mm的“西安交通大学校徽”源图像及其重建图像

重建方法RL算法维纳滤波遗传算法rCC083580836206774

4 灰度源的模拟图像

(a)16阶灰度 (b)16阶灰度模拟结果

(c)64阶灰度 (d)64阶灰度模拟结果

(e)256阶灰度 (f)64阶灰度模拟结果图7 3种灰度在线度为7.15 mm时E字母源图像及其模拟结果

不同灰度阶的E字母源图像与对应模拟获得的编码图像见图7,其中E字母源的灰度值按中心单点的高斯函数分布设计了16、64和256的3种灰度阶数。从图7中显示,随着源图像灰度阶数从16增加为256,编码图像中心强度降低,图像灰度过渡平滑,不同区域间差异不显著。这说明源图像灰度阶由低变高,对应源区上中子发射强度变化梯度由大到小,进而使得编码结果的强度梯度也由大到小变化,因此高灰度阶模拟结果与平滑过渡的实验结果更为相符。当灰度阶数从64增大到256时,模拟结果变化并不明显,这表明E字母源图像按照64阶灰度定义能满足编码图像平滑过渡的要求。相关的模拟参数和结果见表4。

从表4可得,随着源图像灰度阶数的不断增多,虽然合并前源栅元的定义所需的六面体数目变化不大,但是深度优先合并后的六面体数在3种灰度下差异很大。这主要是在较高灰度阶数下,像素点灰度值细微的变化已经导致这些像素点很难合并到一个六面体定义中。随着源栅元中定义的六面体数的增多,更高灰度阶的计算时间不断增加,不过计算结果的最小误差始终控制在1%以下,符合重建算法的重建对象需求。

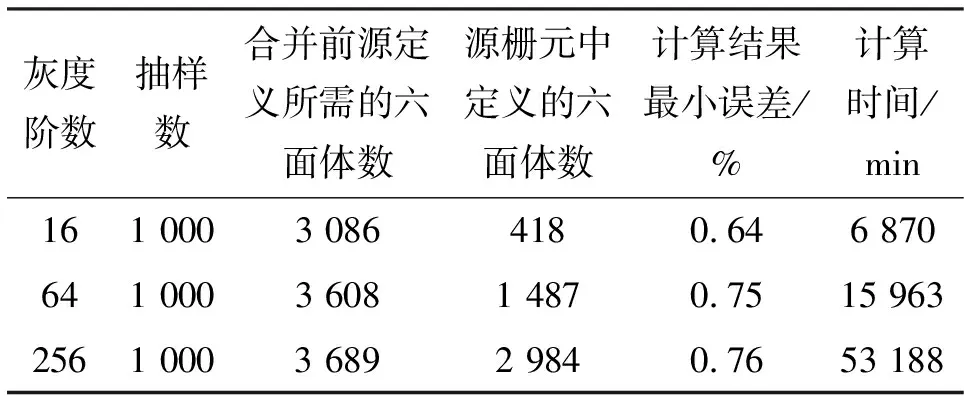
表4 3种灰度在线度为7.15 mm时E字母源图像的模拟参数和结果

5 结论和展望

本文建立了基于深度优先合并方法,采用FIR记录点通量的模拟模型,实现了复杂二值源图像和灰度源图像的定义和模拟。在二值E字母源下,计算结果最小误差没有变化且满足统计要求,计算时间减少为不到合并前直接模拟时间的1/5。对“西安交通大学校徽”进行了复杂二值源的模拟,3种重建方法的结果表明,基于深度优先合并的源定义方法是正确的,对16、64和256的3种灰度阶数的E字母源图像的模拟计算的最小误差小于1%。这样,基于深度优先合并方法的复杂源图像定义方法可进行复杂源图像(二值图像与灰度图像)的定义,进而能对中子及其他粒子编码成像实现高效模拟计算。

此外,聚变反应区的燃烧过程是一个时空耦合的局部与整体均在演化的过程。该演化过程在时间上历经点火—燃烧—最终沉寂等阶段,同时在空间上对应历经等离子体区域尺寸由小到大再到小的变化。在此期间,中子发射的空间强度分布变化十分剧烈,表现为源图像的形状和灰度分布变化十分复杂。可见,采用深度优先合并方法定义的复杂形状源正好适用于对这样复杂变化过程的编码成像实施正过程模拟,进而实现对时空耦合源区各时段图像的重建,所得各时段源图像的局部与整体的边缘可望更为清晰,此有利于正确认识聚变反应区时空耦合演化过程。

[1] PFALZNER S. 惯性约束聚变导论 [M]. 崔旭东, 译. 北京: 原子能出版社, 2011: 1-20.

[2] VOLEGOV P L, DANLY C R, FITTINGHOFF D N, et al. Self characterization of a coded aperture array for neutron source imaging [J]. Rev Sci Instrum, 2014, 85(12): 123506.

[3] VOLEGOV P, DANLY C R, FITTINGHOFF D N, et al. Neutron source reconstruction from pinhole imaging at National Ignition Facility [J]. Rev Sci Instrum, 2014, 85(2): 023508.

[4] WILSON D C, ARAGONEZ R J, ARCHULETA T N, et al. Comparing neutron and X-ray images from NIF implosions [J]. EPJ Web of Conferences, 2013, 59: 04002.

[5] GRIM G P, ARCHULETA T N , ARAGONEZ R J, et al. Summary of the first neutron image data collected at the National Ignition Facility [J]. EPJ Web of Conferences, 2013, 59: 13017.

[6] HURRICANE O A, CALLAHAN D A, CASEY D T, et al. Fuel gain exceeding unity in an inertially confined fusion implosion [J]. Nature, 2014, 506(7488): 343-348.

[7] 张天奎. 快中子编码成像技术中的图像重建方法研究 [D]. 西安: 西安交通大学, 2013.

[8] BRIESMEISTER J F. MCNP: a general Monte Carlo N-particle transport code, Version 4C [R]. Los Alamos, USA: Los Alamos National Laboratory, 2000.

[9] SHULTIS J K, FAW R E. An MCNP primer [M]. Manhattan, USA: Kansas State University, 2006: 16-20.

[10]吴岳雷. 中子半影成像系统关键部件研究及研制 [D]. 西安: 西安交通大学, 2010.

[11]郑向阳. 中子针孔半影成像系统设计方法与针孔试制工艺研究 [D]. 西安: 西安交通大学, 2007.

[12]李成. 惯性约束聚变中子编码孔试制工艺研究 [D]. 西安: 西安交通大学, 2009.

[13]秦娟. 用于瞬态辐射过程诊断的闪烁光纤成像阵列样品试制 [D]. 西安: 西安交通大学, 2008.

[14]西安交通大学核科学与技术系. MCNP-3B/PC程序使用说明书 [R]. 西安: 西安交通大学核科学与技术系, 2004.

[15]BARRERA C. Experimental component characterization, Monte Carlo-based image generation and source reconstruction for the Neutron Imaging System of the National Ignition Facility [D]. Berkeley, USA: University of California at Berkeley, 2007.

[16]X-5 Monte Carlo Team. MCNP: a general Monte Carlo N-particle transport code, version 5 [R]. Los Alamos, USA: Los Alamos National Laboratory, 2003.

[17]陈法新, 郑坚, 李正宏. 用MCNP程序计算针孔成像 [J]. 计算机应用与软件, 2010, 27(7): 185-186. CHEN Faxin, ZHENG Jian, LI Zhenghong. Pinhole imaging calculated by MCNP code [J]. Computer Applications and Software, 2010, 27(7): 185-186.

[18]战元平. 用于快中子成像的闪烁光纤阵列质子串扰抑制方法研究 [D]. 西安: 西安交通大学, 2010.

[19]施灿辉. 基于图像的MCNP数字人体建模与仿真研究 [D]. 合肥: 合肥工业大学, 2003.

[20]RICHARDSON W H. Bayesian-based iterative method of image restoration [J]. Journal of the Optical Society of America, 1972, 62(1): 55-59.

[21]LUCY L B. Iterative technique for rectification of observed distributions [J]. The Astronomical Journal, 1974, 79(6): 745-754.

[22]ZHAO Z G, DING Y K, DONG J J, et al. Richardson-Lucy method for decoding X-ray ring code image [J]. Plasma Physics and Controlled Fusion, 2007, 49(8): 1145-1150.

[23]RESS D, LERCHE R A, ELLIS R J, et al. Neutron imaging of laser fusion-targets [J]. Science, 1988, 241(4868): 956-958.

[24]RESS D, LERCHE R A, ELLIS R J, et al. Neutron imaging of inertial confinement fusion-targets at Nova [J]. Review of Scientific Instruments, 1988, 59(8): 1694-1696.

[25]ZHANG T K, HU H S, JIA Q G, et al. Genetic algorithms applied to reconstructing coded imaging of neutrons and analysis of residual watermark [J]. Rev Sci Instrum, 2012, 83(11): 113505.

[26]金颖. 惯性约束受控热核聚变中的中子成像技术研究 [D]. 大连: 大连理工大学, 2000: 45-63.

(编辑 苗凌)

Highly Effective Simulation Strategy for Coded Imaging of the Complex Fast Neutron Source

ZHANG Fengna1,ZHANG Tiankui2,WANG Dongming1,ZHENG Xiangyang3,HU Huasi1

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. Laser Fusion Research Center, CAEP, Mianyang, Sichuan 621900, China; 3. Nuclear and Radiation Safety Center, MEP, Beijing 100082, China)

To solve the difficulties in complex gray-scale source definition and simulation efficiency, a strategy for defining complex gray-scale source based on the depth-first merger is proposed. A technology of cells merging is used to reduce the number of cells for the source definition and ensure the sampling efficiency of source in Monte Carlo simulation, thus the simulation efficiency of coded imaging of the complex gray-scale source can be increased. When the simulated source is the binary letter E source, the error of simulated coded image of the merged source remains same as that of the source without merging and meets the requirement of the reconstruction for statistics, while the computing time for merged source is reduced to 1/5 of the source without merging. The 16, 64 and 256 gray-scale letter E sources are defined by the definition method of complex gray-scale source based on the depth-first merger, and the corresponding simulations of coded image are also carried out. The errors of simulation results reach less than 1%, which meet the requirement of the reconstruction for statistics. The complex binary source of Xi’an Jiaotong University school badge is defined with the proposed strategy for complex gray-scale source based on the depth-first merger and the corresponding simulation of coded image is carried out, then the reconstructions of the source by three different methods are realized. The strategy for defining complex gray-scale source based on the depth-first merger is verified, so it can be expected to provide a feasible technological approach to enhance the adaptability of diagnosis of the complex capsule implosion process.

fast neutron coded imaging; depth-first merger; complex gray-scale source; Monte Carlo simulation; image reconstruction

2016-02-20。 作者简介:张凤娜(1986—),女,博士生;胡华四(通信作者),男,教授。 基金项目:教育部高校创新研究团队资助项目(IRT1280);陕西省自然科学基础研究计划资助项目(2015JZ001);国家自然科学基金资助项目(11505166)。

时间:2016-05-10

10.7652/xjtuxb201607018

TL65+7

A

0253-987X(2016)07-118-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160510.1523.014.html