粗糙表面弹塑性接触连续光滑指数函数模型与法向接触刚度研究

陈永会,张学良,温淑花,兰国生,王余松,范世荣

(太原科技大学机械工程学院,030024,太原)



粗糙表面弹塑性接触连续光滑指数函数模型与法向接触刚度研究

陈永会,张学良,温淑花,兰国生,王余松,范世荣

(太原科技大学机械工程学院,030024,太原)

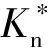
无量纲法向接触刚度;无量纲法向接触载荷;弹塑性接触模型;分形模型;指数模型

工程中的任何接触表面都不是绝对光滑而是粗糙的,它们之间的接触行为往往存在着复杂的多尺度、非线性以及多物理场的特性。对于粗糙表面接触模型的研究,从最早的赫兹接触理论,到后来Greenwood和Williamson进行多方面的假设、利用统计学方法建立的粗糙表面弹性接触模型(即GW模型),以及其他学者建立的适用于极大载荷下的粗糙表面塑性接触模型[1-2],均忽略了弹性变形和塑性变形之间的弹塑性变形区间。针对早期接触模型的缺陷和不足,Chang等利用体积守恒原理建立了粗糙表面弹塑性接触模型,即CEB模型[3]。Zhao等对CEB模型进行了修正,提出了3种变形状态的ZMC模型[4]。Kogut和Etsion利用有限元方法研究了半球体与刚性平面接触时接触载荷、接触面积以及平均接触压力与变形量之间的关系,而且通过曲线拟合得到了分段经验公式,即KE模型[5-6]。ZMC模型和KE模型由于没有考虑临界点处的连续性,因此平均接触压力与变形量之间的关系在临界点都出现了跳跃和不光滑现象。赵永武等采用三次样条函数对ZMC模型进行改进,满足了在临界点连续性和光滑性的要求[7]。此外,Brake采用Hermit多项式插值,也满足了曲线的光滑性和连续性[8]。但是,不管是样条函数还是Hermit多项式的插值函数,都使得粗糙表面弹塑性阶段的平均接触压力与变形量之间的关系曲线出现了振荡现象,使得接触状态的变化过程呈现非单调性。徐超等采用低阶椭圆曲线插值方法进行了弹塑性阶段建模,只拟合了平均接触压力与变形量之间的关系,并利用概率统计方法建立了粗糙表面法向弹塑性接触模型[9],但是弹塑性变形阶段的实际接触面积与变形量之间的关系仍采用了Hermit插值法所给出的关系式,这使得接触参数之间不能很好地匹配。张学良等利用分形理论和KE模型(弹塑性阶段的分段经验公式)推导了粗糙表面三阶段的接触刚度和接触载荷之间的关系,并通过实验验证了模型的正确性[10]。然而如上所述,KE模型存在临界点不连续和跳跃的特点。

针对上述不足,通过观察和分析微凸体在弹性阶段和塑性阶段的接触参数与变形量的关系,本文利用一阶系统阶跃响应函数建立了微凸体弹塑性变形阶段平均接触压力与变形量之间的模型,推导了相关参数,实现了接触参数随变形量的单调、连续、光滑和无跳跃的变化,并与典型模型进行了对比分析,验证了本文模型的可信性。另外,还利用分形理论得到了粗糙表面在弹性阶段、弹塑性阶段和塑性阶段接触时的法向接触刚度和法向接触载荷解析模型,并进行了无量纲化处理,仿真分析了分形维数、塑性指数和无量纲分形粗糙度参数对无量纲法向接触刚度和无量纲法向接触载荷的影响规律,进而分析了无量纲法向接触刚度随无量纲法向接触载荷的变化规律。

1 微凸体弹塑性模型的建立

本模型的建立依然沿用文献[11]中GW模型的假设,这样微凸体的完全弹性阶段与完全塑性阶段的接触参数符合文献[12]中的描述。

完全弹性变形阶段(即δ<δc时)的接触载荷Fe、接触面积Ae以及平均接触压力Pe与接触变形量δ之间的关系分别为

(1)

(2)

(3)

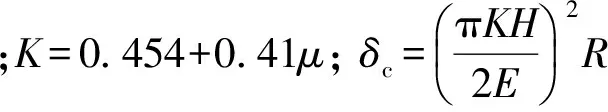
完全塑性变形阶段(即δ>110δc时)的接触载荷Fp、接触面积Ap以及平均接触压力Pp与接触变形量δ之间的关系分别为

(4)

(5)

(6)

弹塑性变形阶段(即δc≤δ≤110δc时)既存在弹性变形区域,又存在塑性变形区域,是两者的混合。在变形量接近δc时,弹性变形区域较大,起主要作用;在变形量接近110δc时,塑性变形区域较大,起主要作用。因而,在弹塑性变形阶段接触参数与变形量的关系是由弹性和塑性的混合所决定的,而且以连续介质力学理论来考虑,弹塑性变形过程是连续的、光滑的和单调的[9]。因此,为了保证这一特点,在δ=δc和δ=110δc两点处,接触面积、接触载荷和平均接触压力与变形量之间的关系必须满足以下要求

(7)

(8)

采用分段拟合的KE模型在δ=δc、δ=6δc和δ=110δc这3个点均出现不连续、不光滑的现象。表1列出了以钢(工程参数为E1=200 GPa,H=5 GPa,μ=0.3,K=0.454+0.41μ,R=1 μm,且下面图1和图2均采用这些数据)为例时的KE模型与本文模型(见式(17))在上述3个点的接触载荷仿真数据对比。从表1中可以看出,KE模型在δ=110δc时接触载荷的相对误差是最大的,达到了7.9%,而本文模型在这3个点的相对误差均为0%。

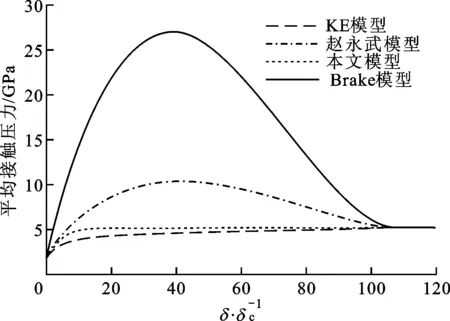
图1 不同模型的平均接触压力对比

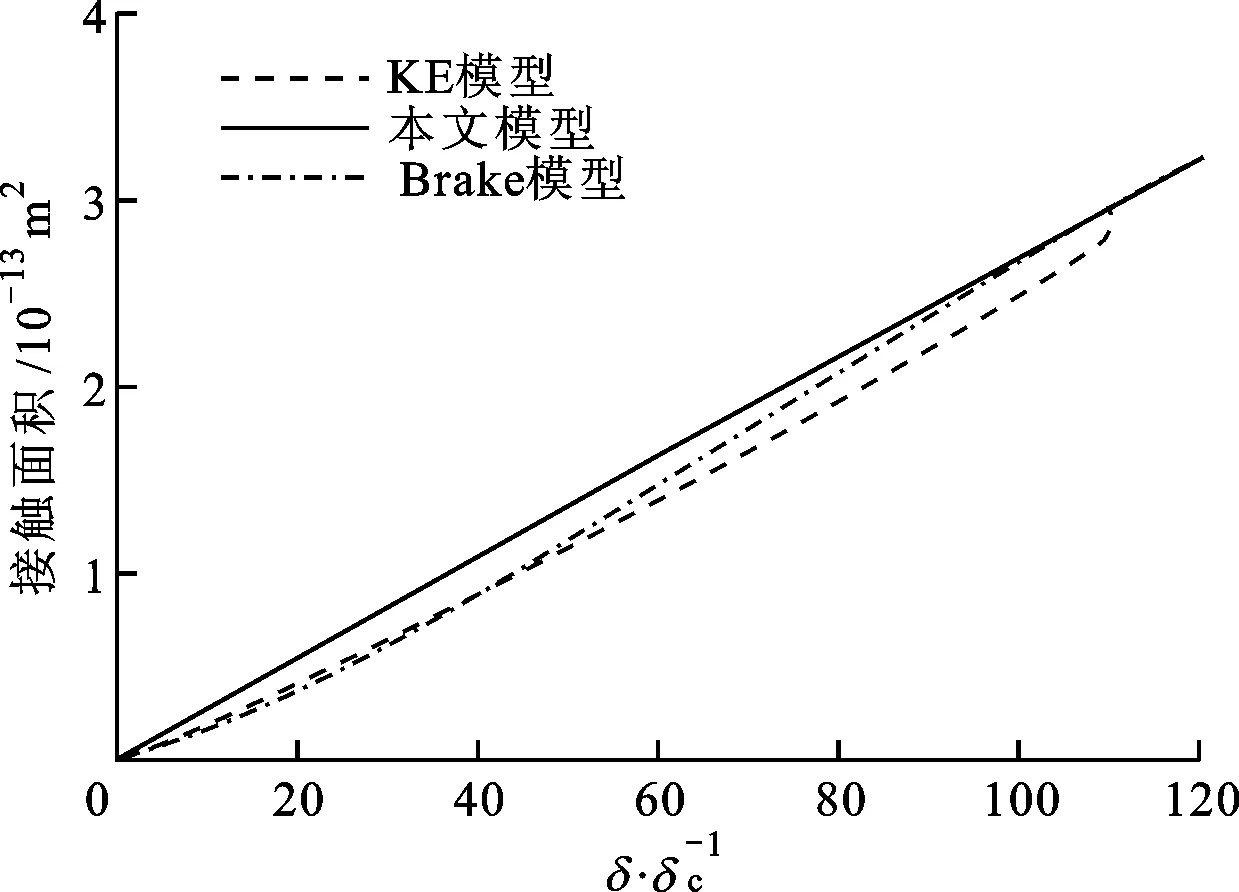
图2 不同模型的接触面积对比

模型参数δ=δc弹性弹塑性一δ=6δc弹塑性一弹塑性二δ=110δc弹塑性二塑性KE模型F/Ne/%25690×10-63026460×10-63033999×10-51734569×10-51713620×10-37914693×10-379本文模型F/Ne/%25690×10-6025690×10-60连续 连续 14693×10-3014693×10-30

文献[7](赵永武模型)和文献[8](Brake模型)对Aep和Fep随变形量δ变化的不连续和不光滑进行了改进,但是,它们的平均接触压力Pep随δ的变化不是单调的。图1表示了KE模型、赵永武模型、Brake模型与本文模型在给定工程参数(表1采用的参数)时的平均接触压力仿真结果对比。文献[9]利用椭圆曲线来对弹塑性阶段平均接触压力的变化进行建模,得到了平均接触压力与变形量之间的关系,见文献[9]中的式(22)。但是,经过推导验证之后发现,其中有部分遗漏的错误。文献[9]式(21)中的椭圆长半轴a为

(9)

而实际的椭圆长半轴应为

(10)

式(9)与式(10)中符号的含义见文献[9]。此外,文献[9]中弹塑性变形阶段的实际接触面积Aep与变形量δ之间的关系是采用文献[8]中的式(16)(利用Hermit插值法)给出的,并没有给出接触载荷Fep与变形量δ的关系。

在考虑上述方法的不足之后,本文尝试采用一阶系统阶跃响应函数的形式对微凸体弹塑性阶段平均接触压力Pep随变形量δ的变化进行建模。为了保证Pep在δ=δc和δ=110δc两个临界点的连续,Pep必须满足式(7)与式(8),由此得到以下条件

(11)

(12)

因此,根据一阶系统阶跃响应的模式,并考虑两个临界点的特点,设定当δ在δc和110δc之间时,Pep与δ之间的关系为

(13)

由于要满足式(11),因此可知

可得

(14)

将式(14)代入式(13)中,可得

(15)

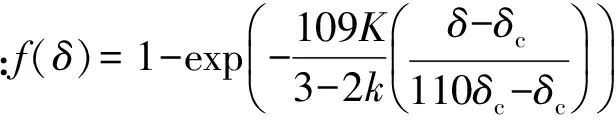
本可以用同样的方法,得到微凸体弹塑性阶段接触面积Aep和接触载荷Fep与变形量δ之间的关系,但是考虑到接触面积和接触载荷在后续推导模型过程中需要进行积分运算,而指数函数与幂函数的乘积不容易积分,无法得到解析模型,因此将f(δ)进行泰勒级数展开,略去高阶项并且进行简化处理,得到微凸体弹塑性阶段的Fep(δ)和Aep(δ)

(16)

(17)

通过表1和图2可以验证,在δ=δc和δ=110δc两个临界点,接触载荷和接触面积与变形量之间的关系是连续的、光滑的和单调的。

2 粗糙表面弹塑性接触模型的建立

根据文献[13],实际粗糙表面微接触点的面积分布密度函数为

(18)

式中:al为最大微接触点的面积;D为粗糙表面的分形维数。

由文献[14-15]可知,粗糙表面微凸体的变形量δ和曲率半径R分别为

(19)

式中:g1(D)=23-Dπ(D-2)/2GD-1(lnβ)1/2;G为粗糙表面的分形粗糙度参数;β为常数,通常β=1.5。

(20)

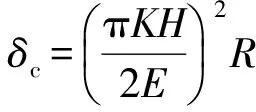
(21)

将式(19)和式(20)代入式(1)中,微凸体在弹性变形阶段的接触载荷Fe(a)可以写成

(22)

由式(22)和式(19),可得在弹性变形阶段微凸体的法向接触刚度

(23)

将式(19)和式(20)代入式(17)中,微凸体在弹塑性变形阶段的接触载荷

(24)

由式(19)和式(24),可以得到微凸体在弹塑性接触阶段的法向接触刚度

(25)

微凸体只有在完全弹性阶段和弹塑性阶段才存在法向接触刚度,而完全塑性阶段不存在法向接触刚度。

同理,可得微凸体在弹塑性阶段的接触面积Aep(a)和平均接触压力Pep(a)分别为

粗糙表面的真实接触面积

(26)

粗糙表面的法向接触刚度只存在于结合面接触变形处于弹性阶段和弹塑性阶段的微凸体上。因此,结合面的总法向接触刚度

(27)

将式(23)、式(25)及式(18)代入式(27)中,可得

(28)

式中

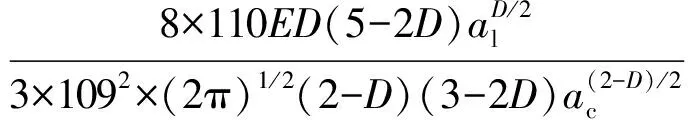
结合面的法向接触总载荷存在于结合面接触变形处于弹性阶段、弹塑性阶段以及塑性阶段的微凸体上,因此,结合面的总法向接触载荷与真实接触面积的关系为

(29)

将式(1)、式(4)、式(24)以及式(18)代入式(29)中,可得

(30)

将式(30)进行无量纲化处理,可得无量纲接触载荷

(31)

式中

将式(28)进行无量纲化处理,可得无量纲法向接触刚度

(32)

式(31)和式(32)分别是粗糙表面接触的无量纲法向接触载荷和无量纲法向接触刚度分形模型,可以发现它们均是一个多变量的复杂函数。

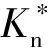
3 粗糙表面接触特性的仿真与分析

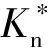
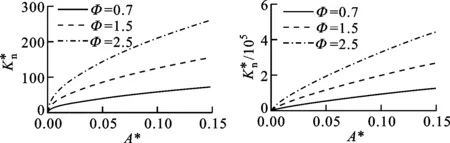
(a)D=1.1 (b)D=1.51

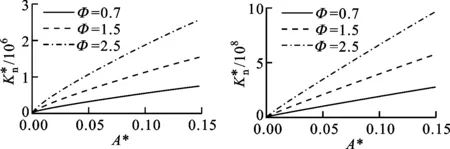
(c)D=1.6 (d)D=1.9图和Φ对的影响(G*=10-10)

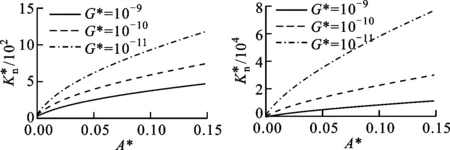
(a)D=1.2 (b)D=1.4

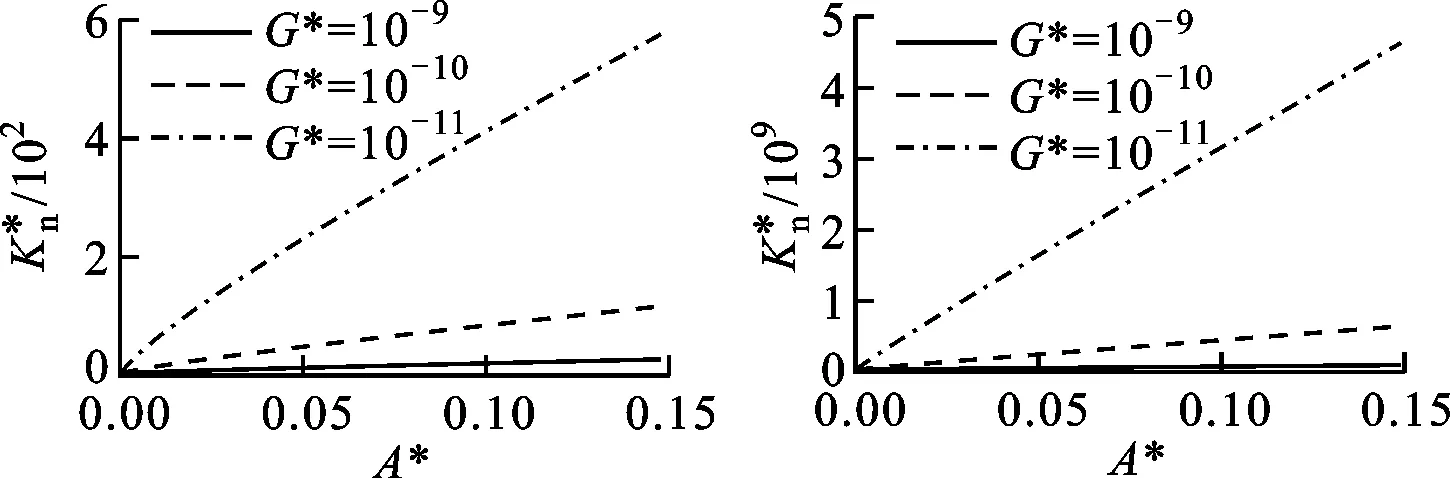
(c)D=1.7 (d)D=1.9图和G*对的影响(Φ=1.5)

图5 D和Φ对的影响(G*=10-10)

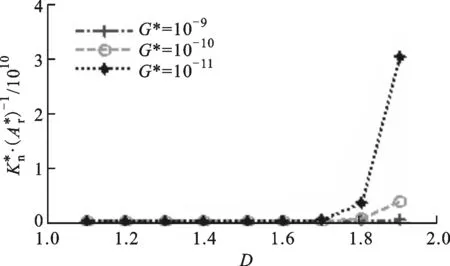
图6 D和G*对的影响(Φ=1.5)

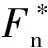
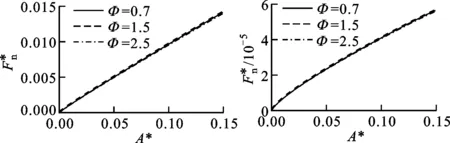
(a)D=1.1 (b)D=1.4

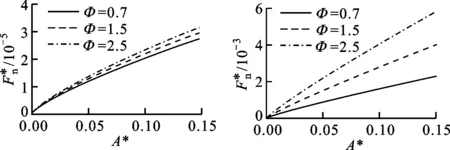
(c)D=1.51 (d)D=1.8图和Φ对的影响(G*=10-10)

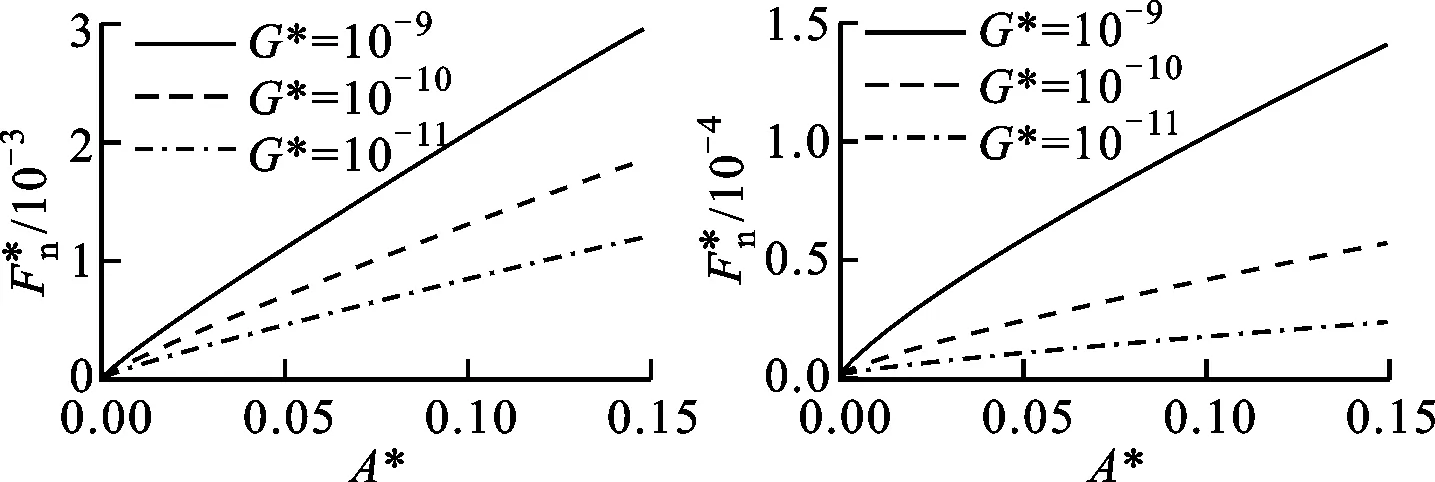
(a)D=1.2 (b)D=1.4

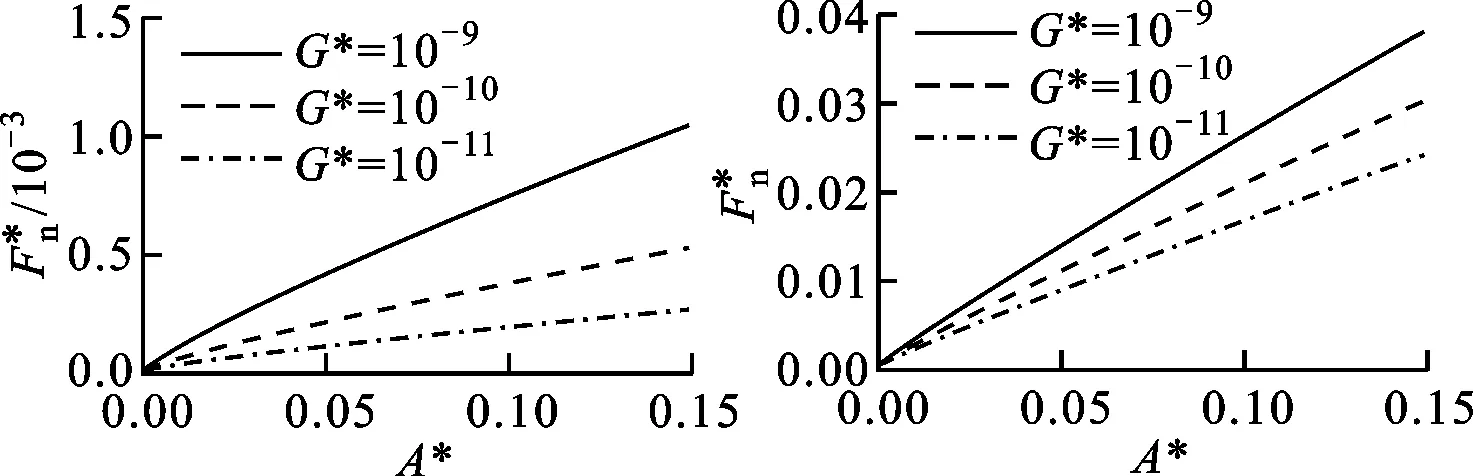
(c)D=1.7 (d)D=1.9图和G*对的影响(Φ=1.5)

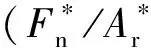
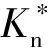
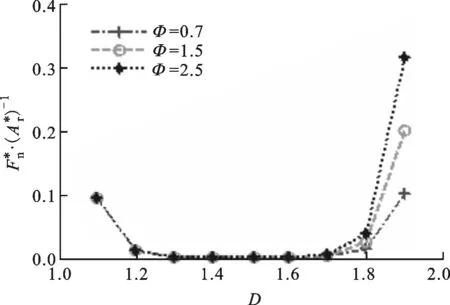
图9 D和Φ对的影响(G*=10-10)

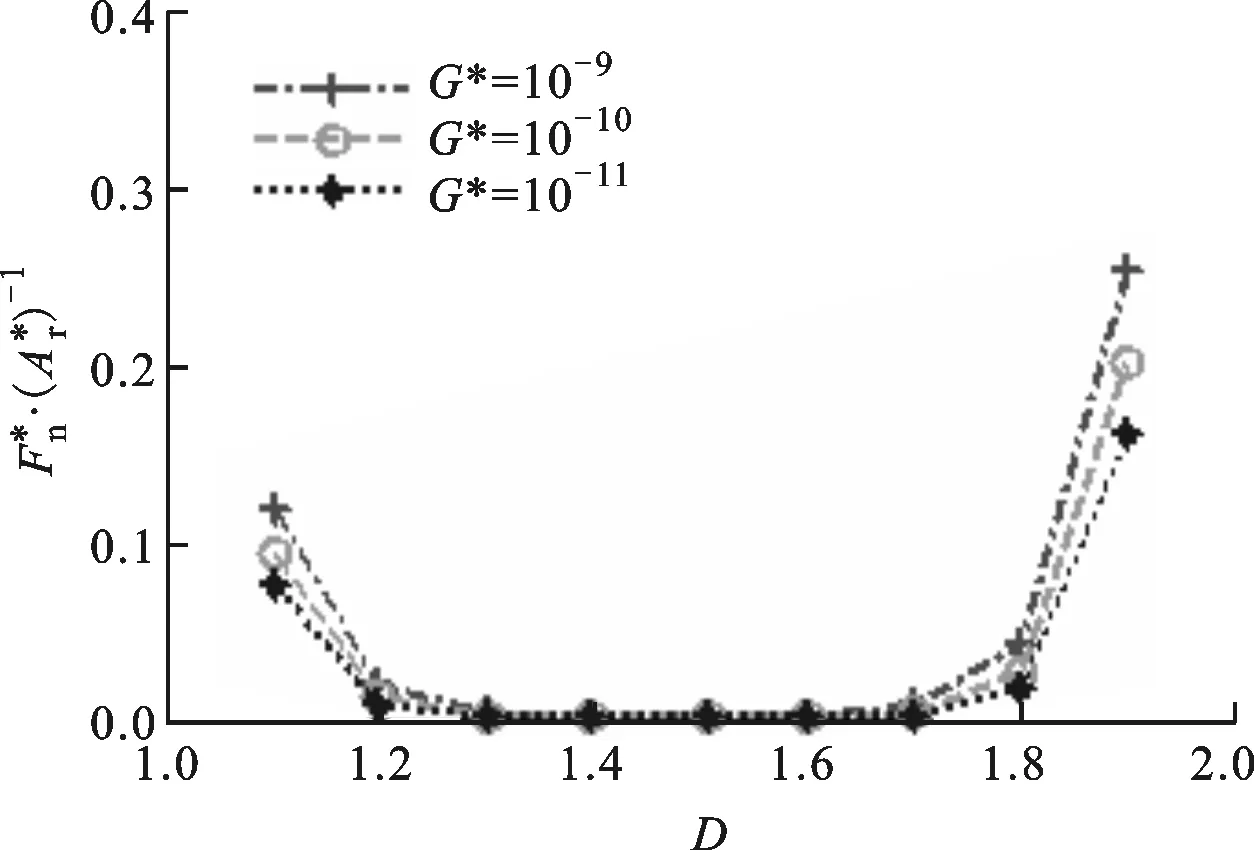
图10 D和G*对的影响(Φ=1.5)

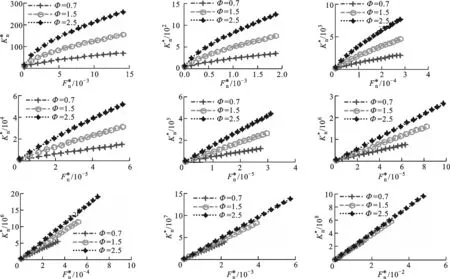
图和Φ对的影响(G*=10-10)

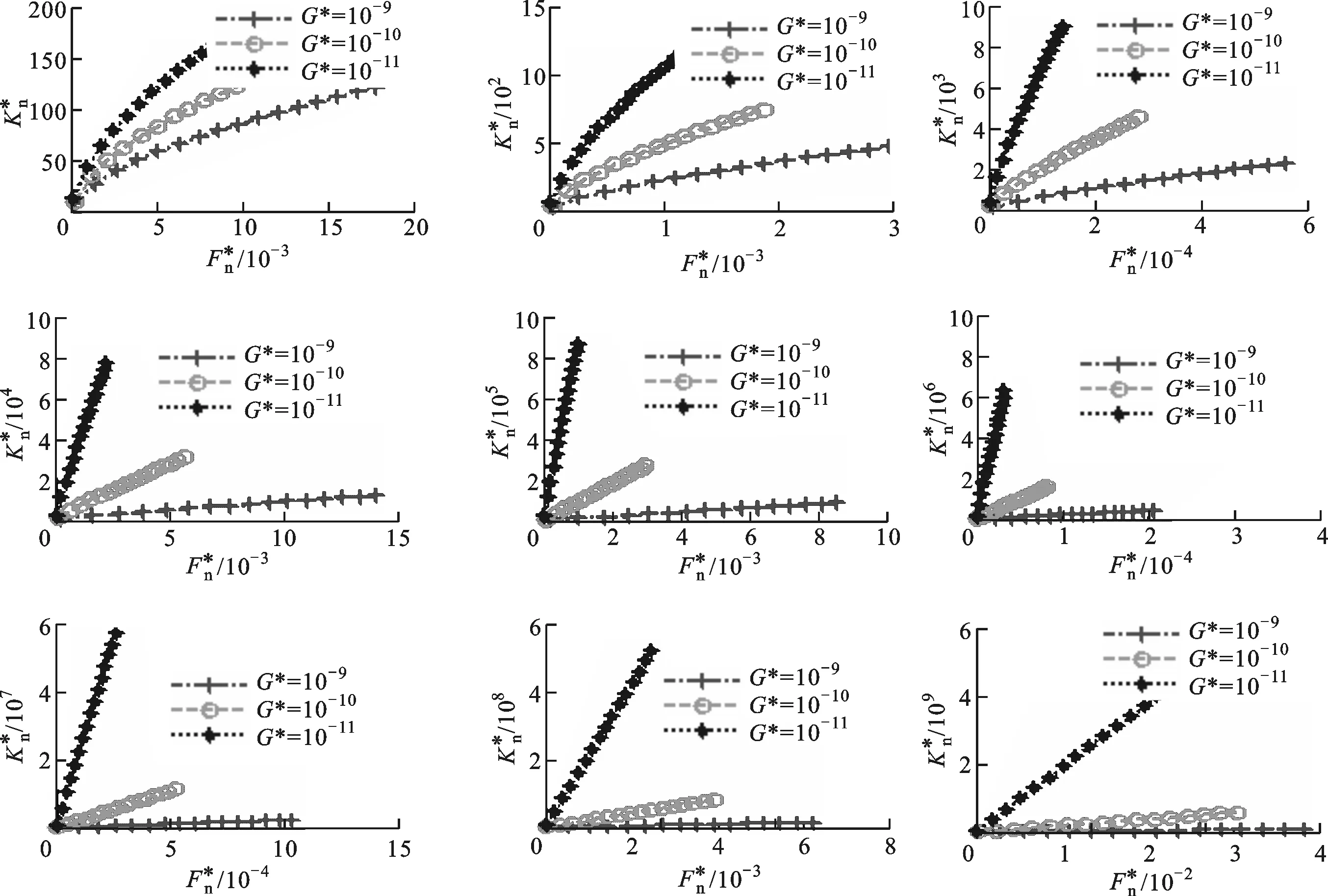
图和G*对的影响(Φ=1.5)

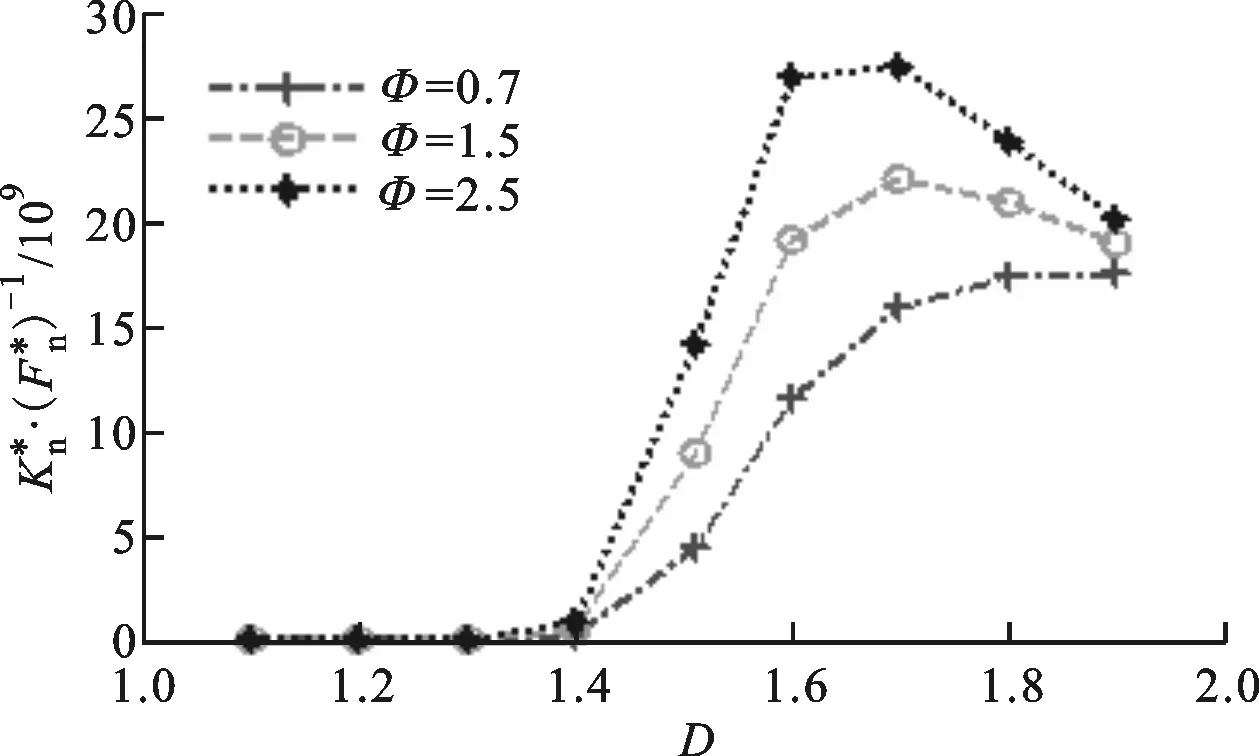
图13 D和Φ对的影响(G*=10-10)

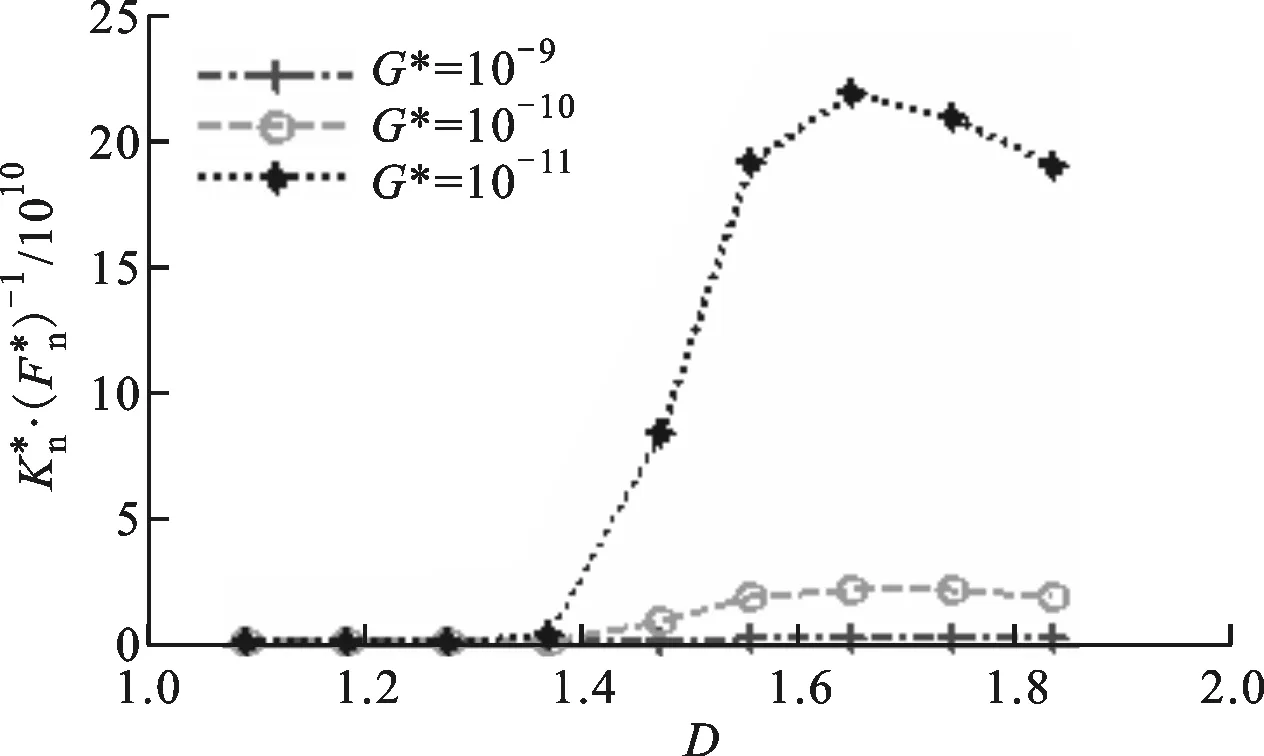
图14 D和G*对的影响(Φ=1.5)

4 粗糙表面法向接触刚度分形模型的应用及实验对比

粗糙表面接触刚度的计算准确与否与结构的固有频率有着密切的关系。利用文献[10]中所给的结合面参数,通过有限元方法计算了哑铃模型的固有频率(螺栓预紧力矩为60 N·m),并且将文献[10]中的结合面法向接触刚度用本文提出的法向接触刚度模型计算结果进行了替换,其他有限元分析中的设置与文献[10]相同,最终计算出哑铃模型的前4阶模态,部分振型图如图15所示。根据模态振型相同的比较原则,将文献[10]和本文模型计算的固有频率与实验值进行了比较,见表2。从表2中可以看出,本文模型计算出的第1、2、4阶固有频率与实验值的误差相对较小,而第3阶固有频率与实验值的误差相对较大。对于机械结构而言,低阶的固有频率相对比较重要,对计算精度的要求也比较高,因此可以利用本文的法向接触刚度模型来计算结构的低阶模态频率,结果较为准确。

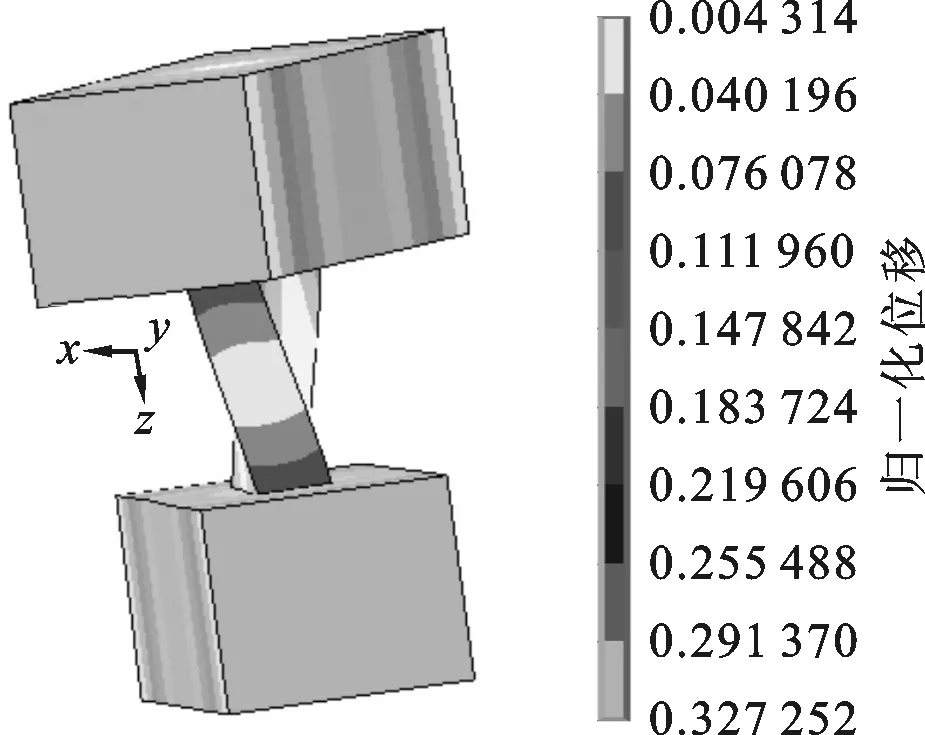
(a)f1=527.45 Hz

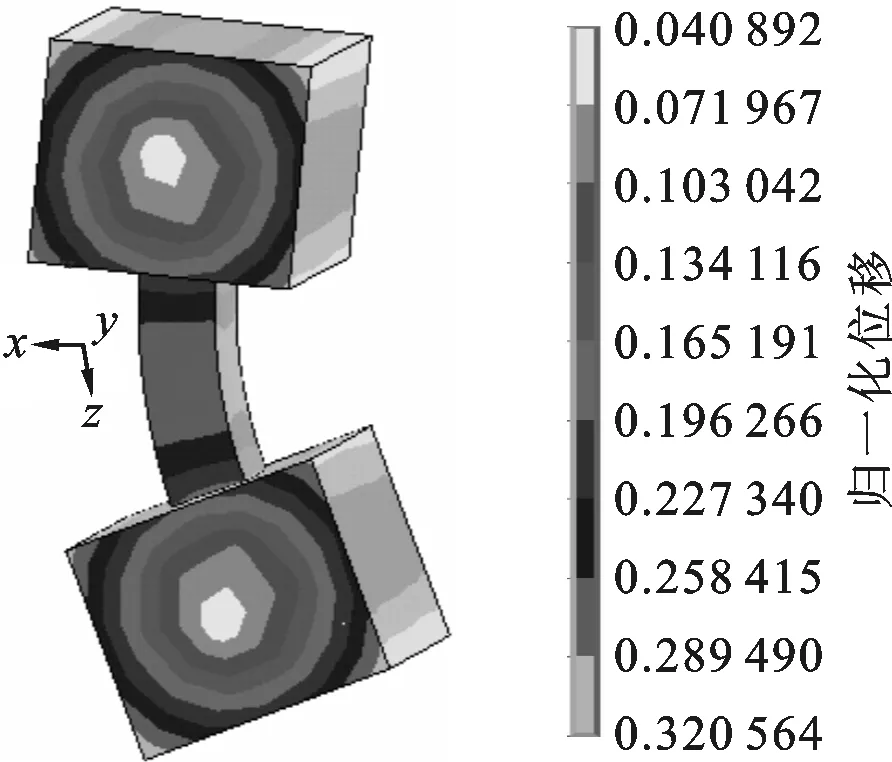
(b)f2=746.90 Hz图15 哑铃模型的计算固有频率和振型

固有频率实验值/Hz本文结果/Hz本文误差/%文献[10]结果/Hz文献[10]误差/%f1542352745-274966-84f2781874690-457336-62f31072394701-11710113-57f42328021752-6521747-66

5 结 论

(1)在GW模型的基础上,建立了一种近似一阶系统阶跃响应模式的微凸体弹塑性接触模型,并与传统的KE模型、Brake模型等做了比较,解决了KE模型在弹塑性阶段是分段拟合的问题,以及Brake模型和赵永武模型[7]的平均接触压力Pep(δ)的非单调性问题,得到了微凸体接触在三阶段(弹性阶段、弹塑性阶段和塑性阶段)的平均接触压力Pep(δ)、接触面积Aep(δ)和接触载荷Fep(δ)与变形量δ之间的关系,并且验证了它们是连续的、光滑的和单调的。

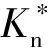
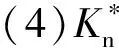
(5)利用本文提出的法向接触刚度模型对哑铃模型的固有频率进行了计算,并将计算结果与实验获得的固有频率进行了比较,验证了本文模型的准确性。

[1] ABBOTT E J, FIRESTTONE F A. Specifying surface quality: a method based on accurate measurement and comparison [J]. Mechanical Engineers, 1933, 55: 569-572.

[2] PULLEN J, WILLIAMSON J B P. On the plastic contact of rough surfaces [J]. Proc R Soc London, 1972, 327: 159-173.

[3] CHANG W R, ETSION I, BOGY D B. An elastic-plastic model for the contact of rough surfaces [J]. ASME Journal of Tribology, 1987, 109(2): 257-263.

[4] ZHAO Y W, DAVID D W, CHANG L. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow [J]. ASME Journal of Tribology, 2000, 122(1): 86-93.

[5] KOGUT L, ETSION I. Elastic-plastic contact analysis of a sphere and rigid flat [J]. Journal of Applied Mechanics, 2002, 69: 657-662.

[6] KOGUT L, ETSION I. A finite element based elastic-plastic model for the contact of rough surfaces [J]. Tribology Transactions, 2003, 46(3): 383-390.

[7] 赵永武, 吕彦明, 蒋建忠. 新的粗糙表面弹塑性接触模型 [J]. 机械工程学报, 2007, 43(3): 95-101. ZHAO Yongwu, LÜ Yanming, JIANG Jianzhong. New elastic-plastic model for the contact of rough surface [J]. Journal of Mechanical Engineering, 2007, 43(3): 95-101.

[8] BRAKE M. An analytical elastic-perfectly plastic contact model [J]. International Journal of Solids and Structures, 2012, 49(22): 3129-3141.

[9] 徐超, 王东. 一种改进的粗糙表面法向弹塑性接触解析模型 [J]. 西安交通大学学报, 2014, 48(11): 115-121. XU Chao, WANG Dong. An improved analytical model for normal elastic-plastic contact of rough surfaces [J]. Journal of Xi’an Jiaotong University, 2014, 48(11): 115-121.

[10]张学良, 陈永会, 温淑花, 等. 考虑弹塑性变形机制的结合面法向接触刚度建模 [J]. 振动工程学报, 2015, 28(1): 91-99. ZHANG Xueliang, CHEN Yonghui, WEN Shuhua, et al. The model of normal contact stiffness of joint interfaces incorporating elastoplastic deformation mechanism [J]. Journal of Vibration Engineering, 2015, 28(1): 91-99.

[11]GREENWOOD J A, TRIPP J H. The contact of two nominally flat rough surfaces [J]. Proceedings of the Institution of Mechanical Engineers, 1970, 185(1): 625-633.

[12]JOHNSON K L. Contact mechanics [M]. Cambridge, UK: Cambridge University Press, 1995: 84-106.

[13]MJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces [J]. Tribol, 1991, 113(1): 1-11.

[14]YAN W, KOMVOPOULOS K. Contact analysis of elastic-plastic fractal surfaces [J]. J Appl Phys, 1998, 84: 3617-3624.

[15]JIANG Shuyun, ZHENG Yunjian. A contact stiffness model of machined plane joint based on fractal theory [J]. ASME Journal of Tribology, 2010, 132(1): 1-7.

(编辑 葛赵青)

Research on Continuous Smooth Exponential Model of Elastic-Plastic Contact and Normal Contact Stiffness of Rough Surface

CHEN Yonghui,ZHANG Xueliang,WEN Shuhua,LAN Guosheng,WANG Yusong,FAN Shirong

(College of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China)

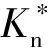
dimensionless normal contact stiffness; dimensionless normal contact load; elastic-plastic contact model; fractal mode; exponential model

2016-01-19。 作者简介:陈永会(1975—),男,副教授;张学良(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51275328)。

时间:2016-04-28

10.7652/xjtuxb201607010

TH113.1

A

0253-987X(2016)07-0058-10

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160428.2222.002.html