基于CARR模型与GARCH模型对VaR的比较研究

郑 兴，王 沁，周炳均，周思娟

(西南交通大学数学学院，四川 成都 611756)

基于CARR模型与GARCH模型对VaR的比较研究

郑 兴，王 沁，周炳均，周思娟

(西南交通大学数学学院，四川 成都 611756)

研究了在一般情形下和极端风险下的风险度量，分别采用基于极差、收益率为变量建模的CARR模型、GARCH模型应用于VaR的计算，结合深证成指的实际数据进行实证分析，分别对比在不同分布下GARCH模型和CARR模型计算出的VaR，最终得出基于在广义伽马分布下CARR模型算出的VaR值，能更加真实地反映深证股市极端情形下风险程度，而基于T分布下的GARCH模型更加真实地反映深证股市一般情形下的风险程度.

VaR；CARR模型；GARCH模型

近三十年来，随着全球金融的发展以及中国金融市场的不断发展与完善，以大规模金融资产为基础出现的金融衍生品越来越多，这些新的金融衍生品在推动国际金融创新的同时也加剧了国际金融市场的剧烈波动，导致的直接后果就是各种全球性的金融危机频发.中国，作为一个全球第二大经济体的发展中国家，在全球性金融危机中难免会遭受冲击，如何进行有效的金融风险度量和管理对目前中国经济的健康持续发展尤为重要.

金融风险管理是现代金融机构管理的基础和核心.而风险管理的核心在于对风险进行度量和评估，全球通用指标是在险价值即风险度量VaR(Value at Risk)[1]，在现有的VaR计算方法中，运用最多的是GARCH类模型计算VaR.

近年来，GARCH模型族被广泛应用于VaR值的计算，根据收益率的计算方法以及结合GARCH模型来求VaR值来看，其用来度量正常市场中的一般风险.而极端事件才是造成风险的主要因素.近三十年内，各种全球性的金融危机频发，1982—1983年，拉美债务危机，1990年，日本经济大衰退，1992—1993年，欧洲货币体系危机，1994—1995年，墨西哥金融危机，1997年，亚洲金融危机，2007年，美国次贷危机，再到2014年，俄罗斯卢布危机，在这些金融极端事件频发时，一个国家的股市出现巨幅下跌的情况，就会在全球范围内引起“多米诺骨牌”效应，此类事件所引发的全球股市循环暴跌引起了证券界乃至国际舆论的广泛关注，针对我国股票市场出现的这种频繁巨幅涨跌动荡现象，准确地度量和管理这些极端风险才是金融风险管理的关键.因此应基于最高价和最低价的极差来建立刻画极端情形下的风险度量模型.

条件自回归极差模型(CARR)，它是由台湾学者周雨田[2]将极差和GARCH模型思想结合提出来的. CARR模型是对极差建立条件异方差模型，包含了每一时间段的最高价和最低价，更充分的提取极端情形下的波动信息.张书林(2011)[3]将参数CARR模型运用到我国黄金现货市场中，通过MZ回归方程和Diebold-Mariano检验，发现参数CARR模型的预测能力比GARCH模型优越.李振(2013)[4]基于CARR模型研究了我国股市波动及其交易量的关系，实证结果表明GCARR-X模型对市场波动非对称性的解释能力较强.可见CARR模型是利用极差刻画波动的优越模型，极差也是一个研究热点，本文也将基于CARR模型来研究极端风险的度量.

1 CARR模型与VaR的计算

1.1 CARR模型的结构

CARR模型是对极差所建立的模型，其结构为:

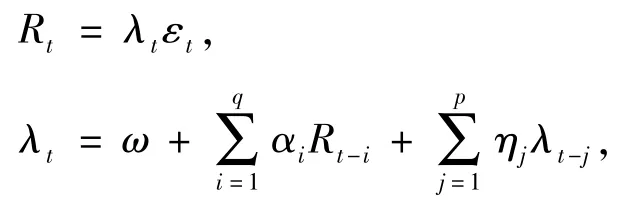
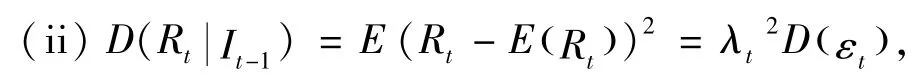
所以，CARR模型的均值和方差随时间波动而波动，这是与GARCH模型完全不同的特点，而且方差的波动具有持续性和聚集性，保持了GARCH模型的特点，而优于GARCH模型，所以利用CARR模型刻画金融市场在极端风险情形下的风险度量更有效.

1.2 CARR模型的参数估计

常用的GARCH模型通常GARCH项[5]和ARCH项都是一阶的，所以常用滞后阶数(p，q)为(1，1)的CARR模型，随机扰动εt常用的分布是指数分布、威布尔分布[6]和广义伽马分布，其相应的似然函数分别为:

且通过对数似然函数就可以估计出不同分布的CARR模型的参数的极大似然估计.

1.3 基于CARR模型计算VaR

所谓VaR，即“Value at Risk”的缩写，含义为“风险价值”，代表在一定置信水平下(confidence Level，通常是95%或99%)，一定持有期内某一资产或投资组合预期可能发生的最大损失值.

确切的说，VaR[7]可表示为:

通常直接利用P(r(t)＜VaR)＝1ˉα来计算VaR.

所以用R(t)来代替r(t)，又因为有了最大值和最小值，就可以刻画极端情形下的风险，基于CARR模型的结构以及极大似然估计的算法可以推倒出极端情况下的:

根据实际数据估计出CARR(1，1)模型中参数ω，α1，η1具体值，就可以计算出λt的值.

算出极差序列Rt均值和方差，再根据VaR计算式得一定1ˉα置信水平的资产VaR值.

1.4 拟合优度检验

拟合优度检验的方法有很多，这里主要介绍赤池信息量准则(AIC准则)[8]，具体如下:

AIC值＝一2∗对数极大似然值十2∗独立参数个数，通过计算AIC统计量评价模型的拟合优度.进行模型选择时，希望AIC值越小越好.

2 GARCH模型与VaR的验证方法

2.1 模型的结构

GARCH(p，q)[9]模型的表达式为:

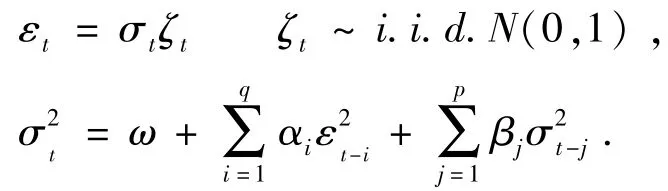
本文基于正态分布，T分布，GED分布[10]下研究基于GARCH模型的VaR的计算问题[11]，已知GARCH模型参数的极大似然估计在MATLAB中可以通过命令garchset指定GARCH模型的结构、命令garchfit对模型进行参数估计以及似然比检验.

2.2 VaR的验证方法-似然比(LR)检验

通过GARCH模型和CARR模型都能得出VaR的值，为了检验VaR值的准确性和有效性，利用似然比方法来检验计算结果，

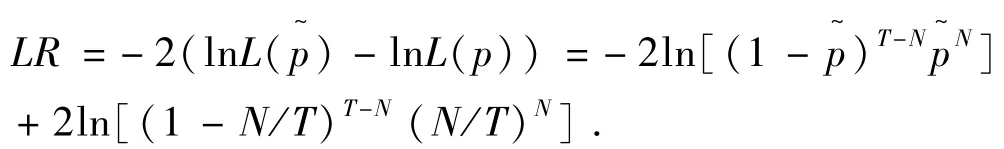
似然比检验统计量中只有P这个估计量需要估计，所以它是服从自由度为1的χ2分布.当β(1)，接受原假设，当，拒绝原假设.接受原假设就说明VaR计算是合理的，而且失败天数的计算就进一步说明VaR计算是有效的.

3 实证研究-CARR模型与GARCH模型对VaR的比较

3.1 数据选取

本文选取了深证成指从2010年1月4日到2014年12月8日共计1194个交易日的数据，对数收益率数据是1193个.其中包括了每日收盘价、最高价、最低价、收盘价，数据来源于大智慧软件.首先定义极差和收益率，极差为:其中为t日最高价、为t日最低价；收益率为，其中为t日的收盘价.首先用Eviews对极差和收益率序列做相应的直观分析，结果如下:

图1 深证成指极差和收益率的序列图Fig.1 Sequence chart of range and rate on return of shenzhen component index

3.2 深圳成指的时间序列特征、平稳性分析

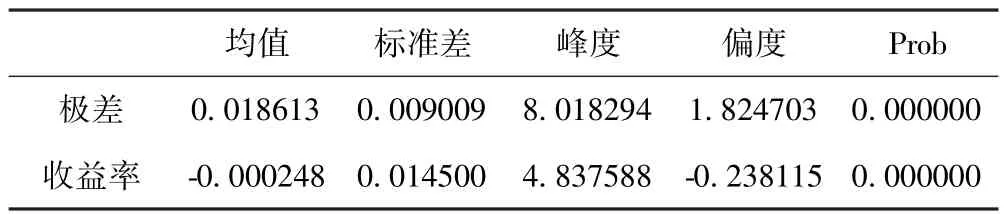
表1 深证成指的基本统计特征Table 1 Basic statistical characteristics of shenzhen component index

由表1可得:从深证成指的极差和对数收益的偏度、峰度以及相应的统计量的值可以看出，深证成指的极差的峰度远远大于3，具有“尖峰”的特性，偏度是大于0的，保证了右偏的特征；收益率序列的峰度比3大一点，不符合正态分布的特征，偏度小于0，是左偏的特征.

表2 深证成指的极差和收益率序列的平稳性检验Table 2 Stationarity test of range and rate on return sequence of shenzhen component index

表2的结论是用单位根方法检验的结果，从P值和5%标准下可以看出序列具有平稳性.

3.3 深证成指极差和收益率序列相关性、异方差性检验

图2 深证成指极差和收益率自相关图Fig.2 Auto-correction chart of range and rate on return of shenzhen component index

极差和收益率的10阶之后计算自相关函数值和偏相关函数值，如图2所示，可以看出极差序列之间相关性显著，但是收益率之间相关性并不显著.

3.4 CARR模型、GARCH模型的参数估计

考虑到两种模型的特殊性，于是基于指数分布，韦布分布，广义伽马分下研究CARR模型，基于正态分布，T分布，GED分布下研究GARCH模型[13].因为分布不同，很难把他们放在一起进行比较研究，所以我们要做的是初步选择每种模型的最佳分布，然后再两者比较，得出最能够拟合原始数据的模型，验证VaR值.用MATLAB做参数估计时建立CARR(1，1)类模型.如下:

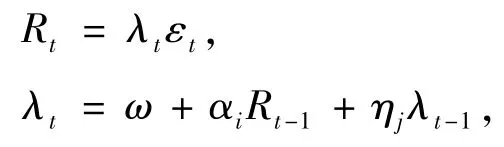
以下是通过MATLAB计算出来的深证成指CARR模型结果:

表3 不同分布下CARR模型的估计结果Table 3 Estimation results of cARR model in different distributions

由表3我们得到极大似然估计值，且通过拟合优度检验的AIC值判断三个模型中GCARR(1，1)模型拟合优度最好，故选择GCARR(1，1)模型.

对收益率序列建立GARCH(1，1)模型，参数估计如下表示:

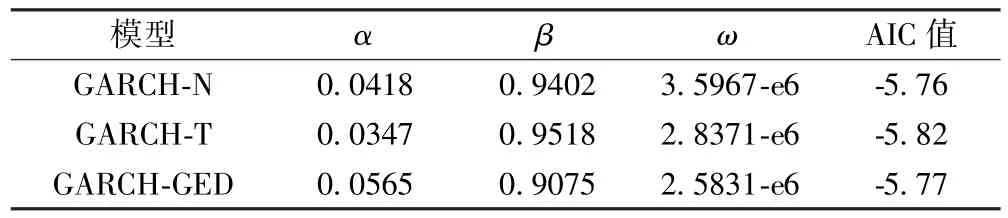
表4 不同分布下GARCH模型的估计结果Table 4 Estimation results of GARCH model in different distributions

由表4我们得到了参数的极大似然估计值，且通过拟合优度检验的AIC值判断三个模型中GARCH-T (1，1)模型的拟合优度最佳，故选择基于T分布下的GARCH(1，1)模型.

T分布下GARCH(1，1)模型的表达式为:

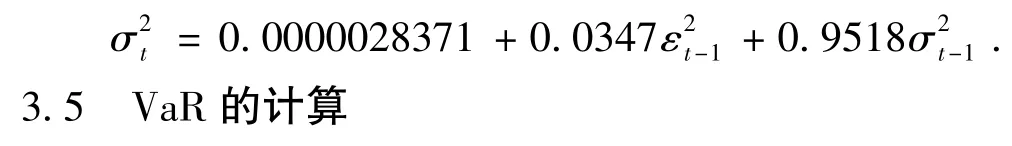
接下来，根据建立的两个最佳模型来计算相应的VaR值.

表5 CARR-G(1，1)和GARCH-T(1，1)[14]的VaR值Table 5 VaR value of CARR-G(1，1)and GARCH-T(1，1)[14]

由表5我们可以看出，根据深证成指数据计算出来的CARR-G模型的VaR均值高于GARCH-T模型，估计的失败天数也相差很明显.无论是在95%还是99%置信水平下，GCARR计算的VaR的失败率都大于5%，这说明模型在95%、99%置信水平下估计的VaR是虽然不精确的，但验证了CARR模型刻画的是极端情况下的风险.而GARCH-T模型计算出来的VaR的失败率都小于5%，并且在95%的置性水平下，GARCH-T模型下VaR的失败接近于5%，由此可以看出对于深证成指数据而言，说明GARCH-T模型估计的VaR比较保守，高估了风险，正验证了GARCH模型刻画的一般状态下的风险.

3.6 VaR的验证

表5根据深证成指数据计算得出的VaR值，需要检验它的准确性和有效性.这里为了评价WCARR (1，1)模型和GARCH-T(1，1)模型的拟合度，即两模型是否能够有效地对资产收益作出解释，需要对估计的VaR进行验证，引入上述似然比检验方法.如下是通过计算得到的似然比率检验统计量，(已知

表6 似然比率统计量Table 6 Likelihood ratio statistics

通过表5我们初步验证GARCH模型计算出来的VaR值较CARR模型合理，这里做进一步验证，如表6，用Kupeic(1995)提出的LR统计量检验，我们可以得出结论:对于深证成指数据而言，不同置信度水平下，T分布下GARCH(1，1)模型下的VaR估计结果是合理的，说明被检验的模型能够很好的拟合深圳成指的实际数据.

综合表5和表6，我们可以得出结论:在广义伽马分布下，利用CARR模型估计深证成指数据的VaR值虽然比较大，这正因为他刻画了极端情形下的风险.而在T分布下，虽然通过变换不同的置信度水平，但GARCH模型下估计的VaR仍都比较合理，而且可以发现99%置信度水平下采用T分布下GARCH(1，1)来估计深圳成指VaR是更合理的.

4 结论

本文为了更加有效地度量金融资产的VaR，考虑到股市的一般风险和极端风险，分别采用能够刻画一般风险的GARCH模型和刻画极端风险的CARR模型，建立基于指数分布，韦布分布，广义伽马分布下建立CARR模型[14]，同样为了对比，又分别建立正态分布，T分布，GED分布下建立GARCH模型，根据不同残差分布的假定下分别对模型进行估计，通过模型的拟合优度检验，选取了基于两种模型的最佳分布: CARR-G模型和GARCH-T模型，然后分别对估计的模型在95%、99%置信水平下计算其对应的VaR值，最后对VaR值进行了失败率检验.本文采用了深证成指这四年的历史最高价，最低价和收盘价计算VaR，通过对以上数据的分析，我们可以看出:在95%、99%的置信水平下，就VaR值而言，CARR-G模型下VaR值的均值较GARCH-T模型要大，这正符合了用CARR模型来刻画极端情形下的风险来估计VaR值的特征.从失败率的角度看，T分布下GARCH模型下计算的VaR值在95%、99%的置信水平下所得的VaR的失败率均小于5%，结合VaR的似然比检验结果，我们可以看出GARCH-T(1，1)模型在95%、 99%置信水平下都比较适合.虽然GARCH-T(1，1)模型下VaR的失败率比较小，但是考虑到该模型刻画的仅是一般情况下的风险，所以就解释了结果过于保守这一说法.

综合可以说明在T分布的GARCH模型下度量的深证股市一般情况下的金融风险合理，而广义伽马分布的CARR模型[15]下度量的极端情况下的金融风险合理，两者都能有效地管理深证股市的资产风险.

[1]BILLO M，PELIZZON L.Value-at-risk:A multivariate switching regime approach[J].Journal of Empirical Finance，2000，7:531-554.

[2]CHOU R Y.Forecasting financial volatilities with extreme values:the conditional autoregressive range(CARR)model[J].Journal of Money，Credit and Banking，2005，37:561-582.

[3]张苏林.我国黄金现货波动率预测能力分析—基于GARCH模型和CARR模型[J].金融理论与实践，2011，8:19-21.

[4]李振.我国股市波动及其与交易量的关系——基于CARR模型的实证研究[D].济南:山东财经大学，2013.

[5]周杰，刘三阳.条件自回归极差模型与波动率估计[J].数量经济技术经济研究，2006，9:101-107.

[6]王敏.非参数条件自回归极差模型及其应用[D].成都:西南财经大学，2013.

[7]山宇.风险价值VaR的计算方法研究[D].重庆:重庆大学，2013.

[8]陈晓峰.AIC准则及其在计量经济学中的应用研究[D].天津:天津财经大学，2012.

[9]BOLLERSLEV T.generalized autoregressive conditional heteroskedasticity[J].Journal of Econo-metrics，1986，31(3):307-328.

[10]鲁浩，周志凯.基于GARCH-GED分布模型的证券投资基金风险度量[J].金融理论与实践，2014，3:51-59.

[11]黄光磊.不同分布条件下金融风险度(VaR)的GARCH/TARCH建模与实证分析[D].武汉:华中科技大学，2007.

[12]黄秀路.基于CVaR风险度量角度的投资组合优化模型的理论与实证研究[D].成都:西南财经大学，2013.

[13]余素红，张世英，宋军.基于GARCH模型和SV模型的VaR比较[J].管理科学学报，2004，7(5):19-25.

[14]龚锐，陈仲常，杨栋锐.GARCH族模型计算中国股市在险价值(VaR)风险的比较研究与评述[J].数量经济技术经济研究，2005 (7):29-36.

[14]龚锐，陈仲常，杨栋锐.GARCH族模型计算中国股市在险价值(VaR)风险的比较研究与评述[J].数量经济技术经济研究，2005 (7):109-116.

[15]王良.VaR风险管理模型的理论与应用[D].大连:东北财经大学，2003.

(责任编辑:付强，张阳，李建忠，罗敏；英文编辑:周序林)

Comparative study of VaR based on CARR and GARCH model

ZHENG Xing，WANG Qin，ZHOU Bing-jun，ZHOU Si-juan
(School of Mathematics，Southwest Jiaotong University，Chengdu 611756，P.R.C.)

The paper studies the risk measurement in general and extreme cases，calculates the VaRs under the CARR Model and GARCH Model which are respectively based on the variables of range and rate on return，conducts the empirical analysis on the actual data of SZSE Component Index，compares the VaRs calculated by GARCH Model and CARR Model in different distributions，and finally obtains VaR value calculated by CARR Model in Generalized Gama Distribution，and the value can more truly reflect the risk degree of the Shenzhen component stock market in extreme cases，and the VaR value calculated by GARCH Model in the T-distribution can more truly reflect the risk degree of the Shenzhen component stock market in general cases.

VaR；CARR model；GARCH model

F272.5

A

2095-4271(2016)05-0567-06

10.11920/xnmdzk.2016.05.017

2016-03-03

郑兴(1991—)，女，汉族，安徽人，硕士研究生，研究方向:金融统计.E-mail:swjtumaster＠163.com

王沁(1973—)，女，汉族，四川人，副教授，研究方向:金融统计、管理科学与工程、时间序列分析.E-mail:wangqin＠home.swjtu.edu.cn

2012年国家自然科学基金项目(71201131)；重庆市群与国的理论及重要实验室开放课题基金资助(KFJJ1404)