壮族初中生数学认识信念现状及其对学业成绩的影响
——以广西A县为例
肖春梅 唐剑岚
(1.河池学院 数学与统计学院, 广西 宜州 546300; 2.广西师范大学 数学与统计学院, 广西 桂林 541004)
壮族初中生数学认识信念现状及其对学业成绩的影响
——以广西A县为例
肖春梅1唐剑岚2
(1.河池学院 数学与统计学院, 广西 宜州 546300; 2.广西师范大学 数学与统计学院, 广西 桂林 541004)
学生的数学认识信念是其数学学业成绩的重要影响因素。通过对272名壮族初中生的调查发现:壮族初中生的数学认识信念处于中等偏上水平,存在非常显著的性别差异;数学知识结构性、数学学习速度和数学学习能力3个维度信念存在显著的年级差异;数学知识确定性信念可以预测初一、初三学生的学业成绩,数学学习速度信念可以预测初二学生的学业成绩。
数学认识信念;壮族;初中生;学业成绩
数学认识信念(Epistemic Beliefs about Mathematics)是指个体对数学知识和知识认识过程的朴素看法或观点[1]。如果简单地说“知与不知”是认知领域研究的问题,“愿与不愿”是情感领域研究的问题,那么“信与不信”则是信念领域研究的问题[2]。影响学生学业成绩的因素很多,有认知因素、情感因素,还有信念因素。从已有研究来看,认知因素、情感因素的研究较多,而信念因素研究还很欠缺。壮族初中生的数学认识信念现状如何?男女生的数学认识信念有差异吗?不同年级学生的数学认识信念有差异吗?数学认识信念对学业成绩产生影响吗?本研究基于以上问题,以广西A县为例开展调查研究,旨在从信念角度为理解壮族初中生的数学学习过程提供实践参考。
1 研究方法
1.1 研究对象
采用分层抽样方法,选择广西A县2所初级中学,剔除非壮族学生,得到样本为壮族学生272人,其中初一年级学生89人,男生55人,女生34人;初二年级学生94人,男生50人,女生44人;初三年级学生89人,男生53人,女生36人。
1.2 研究工具
本研究所采用的量表参考唐剑岚等设计的初中生数学认识信念量表[3],根据壮族学生特点对选项语言进行修改而成,如原量表中的“强烈地同意”改为“非常赞同”等。总量表分为数学知识结构性信念、数学知识确定性信念、数学学习能力信念、数学学习速度信念、数学学习方式信念等5个维度,共20个条目。总量表信度为0.81,分量表信度依次为0.58、0.42、0.55、0.51、0.50,且具有较好的量表结构效度。数学知识结构性信念是指学生相信数学知识是相互独立的,还是相互联系并与生活以及其它学科有联系的;数学知识确定性信念是指学生相信数学知识是绝对正确的,还是不断发展变化的、甚至有误的;数学学习能力信念是指学生相信数学学习的能力是先天注定的,还是可以通过后天努力提高的;数学学习速度信念是指学生相信数学学习是一个循序渐进、逐步积累的过程,还是一个快速的过程;数学学习方式信念是指学生相信数学学习是以被动接受为主,还是以主动建构为主[4]。量表采用李克特(Likert)五级计分,从“非常反对——反对——中立——赞同——非常赞同”分别记1分、2分、3分、4分、5分(反向题反向计分)。
1.3 学业成绩
以研究对象的最近一次全市统一期末考试成绩为学业成绩指标,并将此成绩转换成标准分数。
1.4 施测及数据处理
以班级为单位,在任课教师或班主任的协助下以记名的方式进行测试,记名目的是便于录入学习成绩。采用统一的指导语,时间大约为30 min。发放问卷300份,回收300份,有效问卷272份,回收有效率90.67%。所有数据采用SPSS22录入与处理。
2 调查结果
2.1 壮族初中生数学认识信念总体状况
壮族初中生数学认识信念总体状况见表1。表1显示,壮族初中生数学认识信念所有条目平均分为3.53分。5个维度中除了知识确定性信念,其余各维度得分均在3分到4分之间,这表明壮族初中生的数学认识信念总体情况处于中等偏上水平。但知识确定性信念得分低于3分(2.87分),表明壮族初中生的知识确定性信念水平偏低。
通过对每个维度分析,得出更具体的调查结果。对知识结构性信念,86.4%的学生认为“数学知识相互联系并与生活以及其它学科有联系”;对知识确定性信念,79.0%的学生相信“数学知识是绝对正确的”;对学习能力信念,83.1%的学生相信“数学学习能力通过后天努力可以提高”;对学习速度信念,90.8%的学生相信“数学学习是一个循序渐进、逐步积累的过程”;对学习方式信念,90.4%的学生认为“数学学习是以主动建构为主”。但仍有13.6%的学生认为数学知识之间、数学知识与社会生活、数学知识与其它学科联系不大;仍有16.9%的学生相信数学学习能力是先天注定的;仍有21.0%的学生对教材、教师的观点不敢质疑。

表1 壮族初中生数学认识信念状况描述统计
2.2 不同性别壮族初中生数学认识信念的差异
为了解壮族初中男女生数学认识信念的差异性,我们对男女生的数学认识信念进行了t检验,结果见表2。表2表明,男女生数学认识信念存在非常显著的差异(p<0.01)。进一步分析信念各维度,知识结构性信念存在非常显著的差异(p<0.01)。知识确定性、学习能力、学习速度、学习方式4个维度信念不存在统计学意义上的差异(p>0.05)。
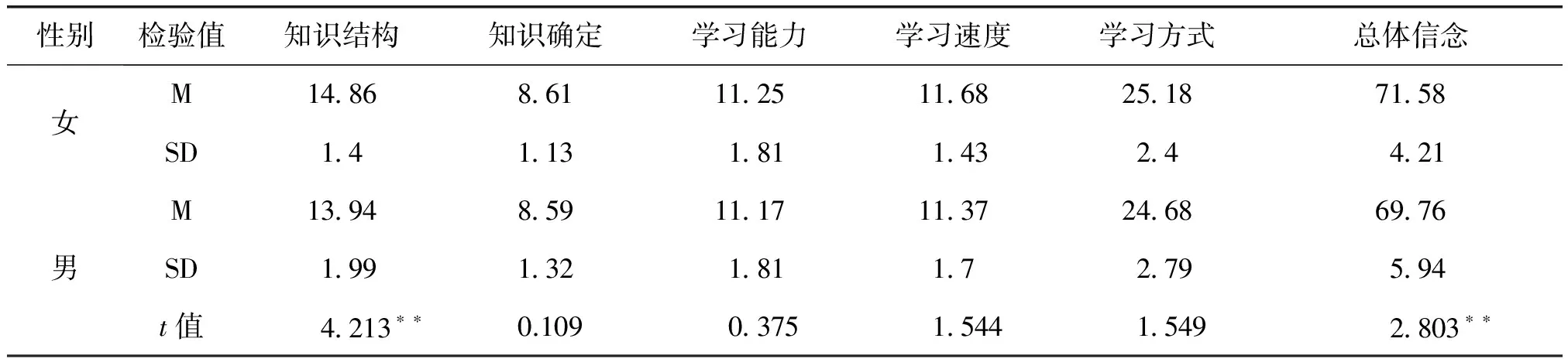
表2 壮族初中生数学认识信念的性别差异
注:*表示p<0.05,**表示p<0.01,下同。
2.3 不同年级壮族初中生数学认识信念的差异
为了考察不同年级壮族初中生数学认识信念的差异,以年级为自变量,以知识结构性、知识确定性、学习能力、学习速度、学习方式5个维度信念为因变量,进行多因素方差分析,结果见表3。表3显示,3个年级的数学认识信念不存在统计学意义上的显著性水平(p>0.05)。进一步分析信念各维度发现,知识结构性、学习速度信念存在非常显著的年级差异(p<0.01),学习能力信念存在显著的年级差异(p<0.05),其它维度不存在显著性差异(p>0.05)。经过Scheffe事后多重比较,在知识结构性信念维度上,初一、初二、初三3个年级呈非常显著的上升趋势(初一<初二<初三);在学习能力信念维度上,初一、初二、初三3个年级呈显著的上升趋势(初一<初二<初三);在学习速度信念维度上,初一得分显著高于初二、初三(初一>初二>初三)。
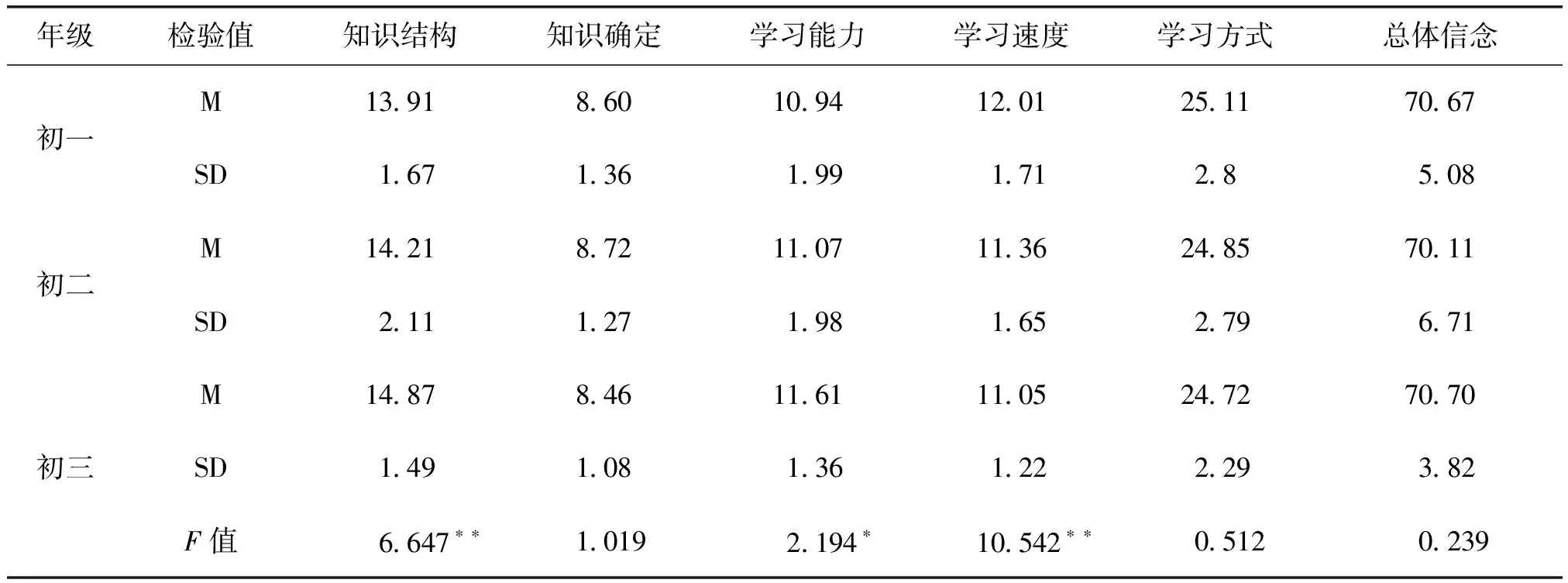
表3 壮族初中生数学认识信念的年级差异
2.4 壮族初中生数学认识信念与学业成绩的相关性
为考察壮族初中生数学认识信念与各年级学生学业成绩的相关性,运用Pearson相关分析法,结果见表4。表4显示,知识结构性、学习速度、学习方式信念均与各年级学业成绩呈显著或非常显著的正相关(p<0.05,p<0.01)。知识确定性信念与初一、初三学业成绩呈非常显著的正相关(p<0.01),而与初二学业成绩无显著相关(p>0.05);学习能力信念与初一、初二学习成绩呈显著的正相关(p<0.05),而与初三学业成绩无显著相关(p>0.05)。

表4 壮族初中生数学认识信念与成绩的相关性
2.5 壮族初中生数学认识信念对学业成绩的回归分析
运用Stepwise逐步回归方法,分析壮族初中生的数学认识信念各维度对学业成绩的回归效应,结果见表5。表5显示,初一、初三的知识确定性信念进入回归模型,对学业成绩产生显著的正面回归效应,也就是说,初一、初三的知识确定性信念对学业成绩的预测力显著;初二的学习速度信念进入回归模型,产生非常显著的正面回归效应,也就是说,初二的学习速度信念对学业成绩的预测力非常显著。
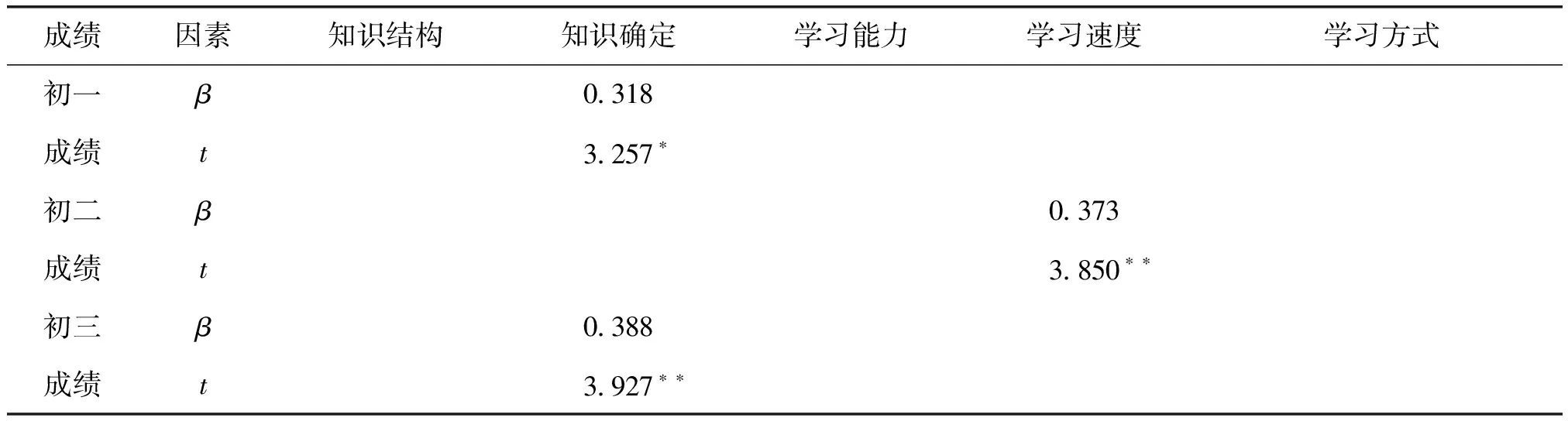
表5 壮族初中生数学认识信念对学业成绩的多元回归分析
3 分析与讨论
3.1 壮族初中生数学认识信念总体现状的分析与讨论
调查结果表明,壮族初中生数学认识信念总体状况处于中等偏上水平,多数学生的数学认识信念发展总体情况较好。已有研究表明[2],教师的教学信念、教学行为是影响学生信念的重要外部因素。壮族初中生数学认识信念发展较好可能得益于以下两个主要方面:一是本地区初中课程改革与全国同步(于2005年秋季学期起全面推行),课程改革已经十年,教师认同和践行新理念与要求。二是近几年“国培计划”、“区培计划”等教师培训项目,这些项目将课程标准解读作为培训的重要内容,并聘请专家对课程标准进行理论解读,聘请当地教研员对课程标准的具体实施进行案例性解读,让教师从理论上和实践上对课程标准有了比较深层次的理解,帮助教师将课程改革的要求落实到具体的教学实践中。如,联系学生生活、社会生产展开数学教学活动,让学生感受“数学与生活、社会的联系”;采用讨论法,让学生体悟“交流讨论对学好数学很有帮助”;注重“过程”教学,让学生体会到“弄懂知识的来龙去脉对学好数学很有帮助”,等。但壮族初中生的数学知识确定性信念水平偏低,也就是说相当一部分学生(79.0%)还不敢于质疑课本和教师,不太相信“通过自己思考获得的知识是可靠的”,这与Mason的研究结果基本一致[5],在他的研究中,学生的知识确定性信念显得滞后,有待进一步发展。这可能由于教师在教学中让学生质疑、独立思考的机会比较少,建议教师在教学中采取适当的教学干预,如创设情境鼓励学生质疑问难,创造条件为学生提供更多独立思考的时间和空间。
3.2 对壮族初中生数学认识信念的性别差异的分析与讨论
调查结果表明,壮族初中男女生数学认识信念存在及其显著的性别差异。从信念各维度看,壮族初中男女生的知识结构性信念存在非常显著的性别差异,女生得分显著高于男生。这与唐剑岚等的研究有些不一致[6],他在对侗族初中生的研究中,男女生知识结构性信念不存在显著差异。这可能是由于不同区域、不同民族文化差异导致的结果。壮族初中男女生的知识结构性信念差异非常显著,可能是由于壮族女性联想较丰富、反应较快,有即兴唱山歌的爱好(在“三月三山歌男女对唱赛”中女性常常是赢家),这使她们更易发现数学知识与生活、与其它学科的联系。此外,还可能与女生的个性品质有关,女生天生情感细腻、观察细心,更能感受和发现数学知识与生活、与其它学科的联系。为此,建议教师在教学中给予男生更多关注,培养他们细心观察,鼓励他们将所学的数学知识运用于解决实际问题中。逐步缩小与女生的差距,提高知识结构性信念水平。
3.3 对壮族初中生数学认识信念的年级差异的分析与讨论
表3表明,壮族初中生数学认识信念不存在年级差异。进一步分析信念各维度,学习速度、知识结构性、学习能力信念存在显著或非常显著的年级差异。经多重比较发现,对于学习速度信念,初一的信念水平显著高于初二和初三;对于学习能力信念,初一、初二、初三的信念水平呈显著上升趋势;对于知识结构性信念,初一、初二、初三的信念水平呈非常显著的上升趋势。其它维度信念不存在显著差异。
对于学习速度信念,初一学生的学习速度信念水平显著高于初二和初三。究其原因,这可能由于初一学生刚进入初中,教师为了让学生适应初中数学学习,适应由数到字母、由算术到代数的抽象过程,对教学进度安排比较合理,解题教学中用于审题、解答时间分配比较恰当,当学生遇到困难时鼓励多花些时间思考,因而学生并不认为数学学习是一个快速完成的过程。但到了初二、初三,为了应付中考,用一年半时间上完两年的教学内容,预留半年时间用于复习以便“冲刺”中考,教师不得不压缩学生探究的时间,更多地采用讲解法和“题海战术”。高强度的练习、海量题目训练,学生无法花较多时间深究数学问题。因而,初二、初三的学习速度信念逐渐动摇,呈下降趋势。这应该引起一线中学数学教师的关注。在教学中,注重对数学知识的结构化处理,帮助学生建构数学知识的命题网络系统,而非仅仅停留在模式化辨认层面,科学合理地预设教学进程,以提高学生学习速度信念的有效性。
对于学习能力信念,随着年级升高,壮族初中生学习能力信念水平呈现显著上升趋势。也就是说随着年级升高,学生越来越相信努力在数学学习中的作用,而不认为数学学习能力是先天注定的。这与Schommer对其他民族学生研究的结果基本一致[7]。究其原因,可能是随着年级升高,数学知识抽象程度越来越高、难度越来越大,要取得好成绩,必须通过坚持不懈地努力。这还可能与壮族学生所处的环境有关,地理环境条件比较恶劣,因而要走出大山、改变命运,必须努力学习考上好高中,进而考上好大学。
对于知识结构性信念,随着年级升高,初一、初二、初三信念水平呈非常显著的上升趋势。也就是说,随着年级升高,壮族初中生越来越相信数学知识的逻辑联系性,越来越感受到数学与物理等其它学科有联系,越来越感受到数学与社会生活有联系。这或许得益于以下几个方面:第一,随着年级升高,数学学习内容逐渐增多,前后知识的逻辑联系越来越凸显,正如人们常说的“数学知识是一环扣一环,如果前面的知识学不好就会影响后续的学习”;随着数学学习内容的增多,与生产、生活联系也自然增多;随着数学、物理等学科内容的增多,它们之间的联系自然也越来越大。第二,本地区使用人教版教材,该版本教材按照新课程标准要求,注重数学知识的“生活化”和生活的“数学化”。教材内容的呈现方式注重采用生活、生产事例引入新知,习题的“生活化”情境较多,有助于学生建构数学知识。第三,不少教师在课堂教学中能够以旧引新、情境引新,能利用身边的壮族文化资源作为课程资源。从个别访谈证实了以上观点。
3.4 壮族初中生数学认识信念与学业成绩的相关性及对学业成绩回归分析与讨论
调查显示,对于初一年级,知识结构性、学习能力、学习方式3个维度信念与学业成绩均存在显著的正相关,表明这3个维度信念对学业成绩产生显著的正面影响;知识确定性、学习速度信念与学业成绩存在非常显著的正相关,表明这2个维度信念对学业成绩产生非常显著的正面影响。进一步采用Stepwise逐步回归法,仅有知识确定性信念进入回归模型,表明知识确定性信念可以预测学业成绩。这与Muis对其他民族学生的研究结果基本一致[8]。
对于初二年级,除了知识确定性信念,知识结构性、学习速度、学习方式信念与学业成绩存在非常显著的正相关,说明这3个维度信念对学业成绩产生非常显著的正面影响;学习能力信念与学业成绩存在显著的正相关,说明其对学业成绩产生显著的正面影响。进一步采用Stepwise逐步回归法,仅有学习速度信念进入回归模型,表明学习速度信念可以非常显著的预测学业成绩。这与Mason对其他民族学生的研究结果基本一致[5]。
对于初三年级,除了学习能力信念,知识结构性、知识确定性、学习速度信念与学业成绩存在非常显著的正相关,表明这3个维度对学业成绩的正面影响非常显著;学习能力信念与学业成绩存在显著的正相关,表明其对学业成绩产生显著的正面影响。进一步采用Stepwise逐步回归法,只有知识确定性信念进入回归模型,表明知识确定性信念可以显著预测学业成绩。这与Muis对其他民族学生的研究结果基本一致[8]。
从以上分析可以看出,壮族初中生的数学认识信念影响其学业成绩。比如,持有“数学知识是可误的,可以怀疑的”认识信念的学生,比持有“数学知识是绝对正确的,永远不变的”认识信念的学生,学习成绩要好。这可能是因为认为数学知识的正确性是可以怀疑的学生,常常会提出“对不对”“为什么对”“为什么错”等问题,促使其对数学问题进一步思考与探究,对数学知识理解更深刻,从而学习成绩就会更好。
4 结论
(1)壮族初中生的数学认识信念处于中等偏上水平,数学知识确定性信念有待进一步发展。
(2)壮族初中生的数学认识信念存在非常显著的性别差异,女生的数学认识信念水平显著高于男生。
(3)壮族初中生的数学认识信念不存在年级差异,但数学学习能力、数学知识结构性、数学学习速度3个维度信念存在显著或非常显著的年级差异。
(4)壮族初一学生的数学知识确定性信念对学业成绩有显著的预测力,初二学生的数学学习速度信念对学业成绩具有非常显著的预测力,初三学生的数学知识确定性信念对学业成绩具有非常显著的预测力。
[1]唐剑岚.学生数学认识信念的研究述评[J].数学教育学报,2007(1):29-33.
[2]喻平.教师的认识信念系统及其对教学的影响[J].教师教育研究,2007(4):18-22.
[3]Tang Jianlan. Exploratory and Confirmatory factor Analysis of an Epistemic Beliefs Questionaire about Mathematics for Chinese Junior Middle School Students[J].Journal of Mathematics Education,2010(2):56-62.
[4]肖春梅,喻平,颜丽增.高中生数学认识信念的现状及对学习的影响[J].数学教育学报,2007(2):40-43.
[5]Mason L. High school students' beliefs about math, mathematical problem solving, and their achievement in math: A cross-sectional study[J]. Educational Psychology, 2003(23):73-85.
[6]唐剑岚,韦华益,黄德诚.侗族初中生数学认识信念的调查与思考[J].内蒙古师范大学学报(教育科学版),2013(8):147-150.
[7]Schommer M, Duell O, Hutter R. Epistemological Beliefs, Mathematical ProblemSolving Beliefs, and Academic Performance of Middle School Students[J]. The Elementary School Journal, 2005,105(3):289-304.
[8]Muis, KR.Personal Epistemology and Mathematics: A Critical Review and Synthesis of Research[J]. Review of Educational Research, 2004,74(3):317-380.
[9]唐剑岚,蒋蜜蜜,肖宝莹.数学认识信念:影响数学学习过程的重要变量[J].课程·教材·教法,2014(6):61-66.
[责任编辑 刘景平]
Current Situation of Junior High School Students’ Mathematics Epistemic Beliefs in the Zhuang Nationality and Its Influence on Students’ Mathematical Achievement ——Taking A County in Guangxi Autonomous Region as an Example
XIAO Chunmei1, TANG Jianlan2
(1.School of Mathematics and Statistics, Hechi University, Yizhou, Guangxi 546300; 2.School of Mathematics and Statistics, Guangxi Normal University, Guilin, Guangxi 541004, China)
Students’ mathematics epistemic beliefs are important factors that affect their mathematical achievement. Through a survey of 272 junior high school students in the Zhuang nationality, the authors find that Zhuang nationality junior high school students’ mathematics epistemic beliefs are at a level above average, and there is a distinctive difference between genders. And there is a significant difference in three dimension beliefs in various grades, including mathematics knowledge structure, mathematics learning speed and mathematics learning ability. Mathematics knowledge certainty beliefs can predict the mathematics achievement of junior high school students in grade 1 and grade 3,and mathematics learning speed beliefs can predict the mathematics achievement of junior high school students in grade 2.
mathematics epistemic beliefs; the Zhuang nationality; junior middle school students; mathematical achievement
G625.5
A
1672-9021(2016)05-0122-07
肖春梅(1968-),女,广西东兰人,河池学院数学与统计学院副教授,主要研究方向:数学教育;唐剑岚(1974-),男,湖南永州人,博士,广西师范大学数学与统计学院教授,硕导,主要研究方向:数学教育。
教育部人文社会科学研究青年基金资助项目(12YJC880093);广西高等教育本科教学改革工程立项项目(2016JGA315);河池学院硕士专业学位授予单位立项课题(2015YTB001)。
2016-09-19

