面层沥青混合料弯曲劲度模量取值研究

田宇翔，马 骉，周雪艳，黄 维

(长安大学特殊地区公路工程教育部重点实验室，西安 710064)



面层沥青混合料弯曲劲度模量取值研究

田宇翔，马 骉，周雪艳，黄 维

(长安大学特殊地区公路工程教育部重点实验室，西安 710064)

沥青混合料的弯曲劲度模量是沥青路面结构设计与性能评价的重要参数。对面层沥青混合料而言，模量的大小与材料的力学与路用性能密切相关。但目前研究中对沥青路面结构设计与行为分析中合理模量参数取值的重要性认识较为不足，针对模量取值与预测方面的研究相对较少。本研究通过收集既有沥青混合料弯曲劲度模量数据，建立模量数据库，通过适当的数学处理获得不同条件下的混合料模量代表值。结果表明：沥青混合料弯曲劲度模量代表值随温度、沥青用量与沥青类型的变化基本符合既有研究中获得的变化关系，对大数据进行数学处理获得的代表值具有较好的代表性；利用数学回归方法，建立不同条件下的混合料模量预测方程，经验证所建立的模量对数模型具有较高的拟合精度与再现性，可为沥青路面结构设计与行为分析中模量参数的取值提供参考。

弯曲劲度模量； 代表值； 温度； 材料参数； 预测模型

1 引 言

沥青混合料是一种非线性弹、粘、塑性材料，随着温度等条件的变化，混合料呈现出不同的性质状态，直接影响沥青路面的耐久性，具体表现为高温稳定与低温抗裂性能，沥青路面的稳定性在一定程度上体现为路用材料抵抗变形的能力，车辙及开裂等病害的发生均为抗变形能力不足或变形能力较差导致，这种材料的变形特性可由模量的大小表征，模量较高时材料的塑性变形较小，抗变形能力较强；模量较小时，材料变形能力较强，低温延伸性能较好[1，2]。

现有规范中通过低温弯曲试验评价沥青混合料的低温性能，其中弯曲劲度模量与材料的抗弯拉强度、弯拉应变密切相关，是表征强度与变形的综合性指标，用于反映混合料的延伸与抗裂性能，是沥青路面结构设计与低温性能评价的重要参数与指标[3]。由此可见，模量的取值是沥青路面结构设计合理与否的前提与基础，与沥青路面设计和性能评价有着重大的相关性。但目前针对这一方面的研究相对较少，对沥青路面、尤其是面层结构设计与分析中合理模量取值的重要性认识较为不足[4]。

本研究以沥青混合料弯曲劲度模量取值为研究方向，通过收集汇总既有混合料弯曲劲度模量试验数据，建立模量数据库，以级配、沥青、试验条件为参数对数据进行分类整理，通过数学方法进行数据处理，获得不同条件下模量代表值，对比分析不同因素下模量代表值的变化趋势，以确定代表值的合理性与准确程度；对混合料弯曲劲度模量与温度的变化进行回归拟合，建立模量预测模型，引入修正系数对不同粒径、沥青类型下的模量预测结果进行修正，以扩大模型预测范围与精度，为沥青路面模量参数的取值提供参考依据。本文具体研究方案见图1。

图1 具体研究方案Fig.1 The concrete research plan

2 模量试验数据收集与分析

2.1 弯曲劲度模量数据收集

以沥青路面、沥青混合料和模量为关键词检索各类硕博学位论文、国内外优秀期刊及会议论文，共检索文献20012篇，共计各类学术期刊16000余篇，优秀硕博学位论文3000余篇，国内外会议论文800余篇，经初步筛选后选取其中7500篇下载整理，进行模量数据收集。以试验条件与材料参数为主因素，经反复筛选检验，剔除重复、无效或条件缺失的数据。最终在224篇文献中提取沥青混合料弯曲劲度模量数据共1283组，数据来源包含各类硕博学位论文87篇，国内外优秀期刊137篇。

2.2 弯曲劲度模量数据总体分析

由于研究中收集的沥青混合料模量数据来源各不相同，模量试验的研究目的与试验方案各异，首先应从级配类型、沥青结合料类型和温度等主要因素出发，掌握并分析模量数据的总体分布情况，以便进行进一步研究。模量具体分布情况如图2所示。

由图2可知，从级配看，弯曲劲度模量数据主要集中在AC-13和AC-16等类型下，其中AC-13下模量数据最多，AC-16下次之，分别占总量的29%和21%；从沥青类型看，模量数据主要集中在道路石油沥青、SBS和SBR改性沥青三种类型下，其中道路石油沥青条件下数据最多，可占总量32%以上，SBS与SBR条件下次之；从试验温度看，弯曲试验温度条件从-20 ℃至20 ℃不等，其中-10 ℃下数据最多，占总量60%以上，其它温度下数据较少。

图2 沥青混合料弯曲劲度模量数据分布图(a)各级配下模量数据分布; (b)各沥青类型下模量数据分布;(c)各温度下模量数据分布Fig.2 The data distribution of bending stiffness modulus(a)modulus distribution by gradation; (b)modulus distribution by asphalt type;(c)modulus distribution by temperature

3 弯曲劲度模量数据代表值确定

3.1 模量数据筛选与整理

根据模量数据分布情况，选取AC-13与AC-16混合料模量为主对象。由于数据受试验偶然性及随机性影响，即使在相同的试验条件下获得的数据跨度及离散性仍较大，加之数据量较大，不利于进行进一步分析，因此，应先对数据进行适当的选择与处理，获取不同条件下的模量代表值进行分析，以保证研究结果的可靠程度与代表性。以下以-10 ℃下AC-13道路石油沥青混合料弯曲劲度模量代表值的计算过程为例，介绍模量代表值的计算方法。

AC-13混合料在-10 ℃下的弯曲劲度模量数据分布区间由1100 MPa至14000 MPa不等，数据跨度较大，首先绘制不同区间的模量数据柱状分布图，结果见图3(a)。

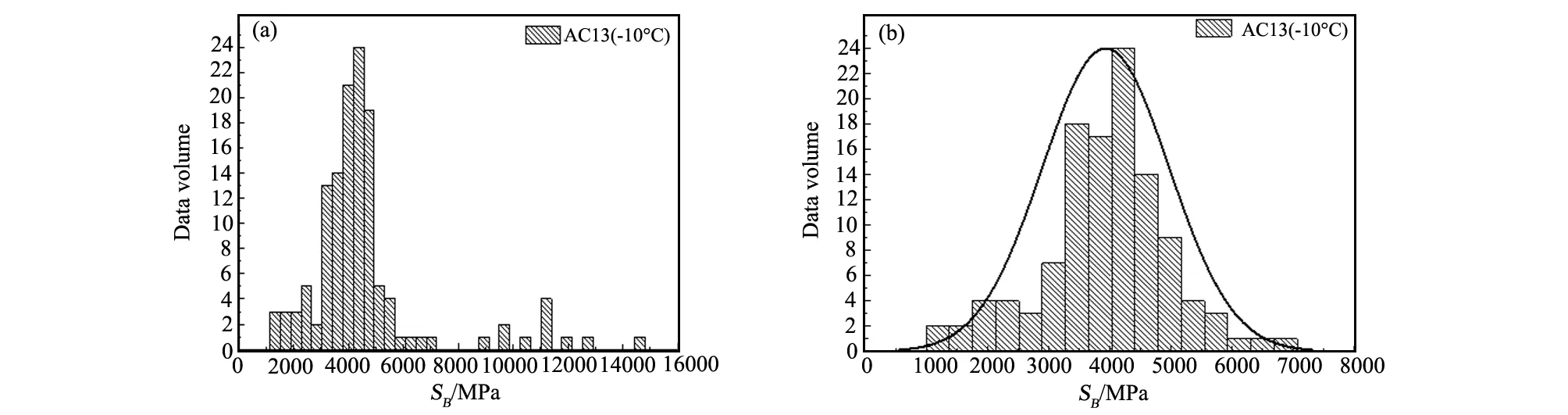
图3 AC-13混合料弯曲劲度模量数据分布图(a)模量数据柱状分布图;(b)数据处理后的柱状分布图Fig.3 AC-13 mixture bending stiffness modulus distribution histogram(a)the data distribution histogram;(b)the data distribution histogram after processing

由图3(a)可知，模量数据主要集中在2000 MPa至7000 MPa之间，并存在模量高出主要区间的偏高现象，应验证异常数据所在文献，查找偏高或偏低数据的原因，以确定是否予以剔除。经查找验证，高模量数据来源为《沥青胶浆延度与混合料低温抗裂性能研究》[5]，该研究通过较大幅度改变粉胶比以研究粉胶比与沥青混合料低温抗裂性能的关系，为特殊条件下的低温劲度模量，不具普遍性与代表性，可予以剔除，剔除异常数据后，对剩余数据重新进行整理，具体分布情况见图3(b)。

3.2 模量数据正态分布检验与代表值确定

如图3(b) 所示，用正态检验方法对图中数据进行正态分布检验，具体检验结果见表1。

表1 正态分布检验结果Table 1 Normal distribution test results

如表1所示，经过分析检验及试算，在0.1的显著水平条件下，数据满足正态条件下0.00868<0.05的要求，数据基本服从正态分布。在此基础上，弯曲劲度模量置信区间按式(1)计算。

(1)

式中：SB-弯曲劲度模量代表值，MPa；

Za-保证率系数，按90%保证率取1.645；

S-各模量的标准差。

由于弯曲劲度模量主要用于表征沥青混合料的低温性能，根据最不利原则要求，在90%的保证率下选取置信下限作为弯曲劲度模量代表值。以同样的方法确定其它条件下的模量代表值，代表值结果汇总见表2。

表2 沥青混合料弯曲劲度模量代表值汇总表Table 2 The representative value summary sheet

4 模量代表值与试验参数关系研究

4.1 模量代表值与温度关系分析

图4 沥青混合料弯曲劲度模量代表值与温度的变化关系(a)AC-13;(b)AC-16Fig.4 Bending stiffness modulus representative value variation versus temperature

在确定模量数据代表值的基础上，根据数据分布情况，选取AC-13与AC-16道路石油沥青与SBS、SBR改性沥青混合料，对其在最佳沥青用量下的模量代表值随温度的变化进行分析，以温度为变量，绘制AC-13与AC-16混合料弯曲劲度模量代表值随温度的变化趋势，结果如图4所示。

由图4可知，混合料模量代表值随温度升高总体呈减小趋势，根据增减幅度不同可将其变化过程划分为-10 ℃以下、-10 ℃至0 ℃和0 ℃以上三个阶段。-10 ℃以下时，模量随温度升高减小速率较慢；在-10 ℃至0 ℃时，随温度升高模量的减小速率明显加快，与-20 ℃相比，-10 ℃下两种级配模量代表值分别减小约28%与25%，而相比-10 ℃，0 ℃下的模量代表值分别减小约54%与78%；0 ℃以上时，模量随温度升高，减小幅度逐渐变小，最终在10 ℃至15 ℃范围内趋于稳定。

从破坏角度看，沥青混合料在高温与低温下分别呈柔性与脆性破坏，混合料脆化破坏温度临界值基本处于-10 ℃附近；从变形角度看，-10 ℃至0 ℃时沥青由弹性向粘弹性转化，弯拉应变增加速率变大，弯曲劲度模量减小较快，之后沥青随温度上升逐渐呈粘塑性体状态，弯曲劲度模量变化趋于缓和[6,7]。

4.2 模量代表值与沥青用量关系分析

为研究沥青用量对混合料弯曲劲度模量的影响，选取-10 ℃下AC-13与AC-16混合料模量代表值为对象，对比分析道路石油沥青、SBS与SBR改性沥青混合料在4.5%、5%、5.5%、6%与6.5%沥青用量下的变化趋势，结果如图5所示。

图5 沥青混合料弯曲劲度模量代表值与沥青用量的变化关系(a)AC-13;(b)AC-16Fig.5 Bending stiffness modulus representative value variation versus asphalt dosage

由图5可知，-10 ℃下，AC-13道路石油沥青与改性沥青混合料模量代表值随沥青用量的增大呈凸型抛物线变化，相比4.5%沥青用量，6.5%时的道路石油沥青与SBS改性沥青混合料模量代表值分别减小了约6%与9%，模量在5.5%至6%附近达到峰值后以较快速率减小，与5.5%相比，道路石油沥青与SBS改性沥青在6.5%时模量代表值分别减小12%与14%；AC-16下模量变化同样呈凸型抛物线变化，模量峰值处于5%至6%区间内，与模量代表值最小值相比，峰值时高出15%以上。

沥青用量的改变会对沥青混合料的结构状态、整体强度与抗变形能力造成影响，同时会造成不同温度下混合料粘弹状态、力学性能及流动能力的显著改变，对改性沥青而言，沥青含量会与改性剂及外掺剂用量的变化构成连锁反应，使沥青混合料的材料性能更加趋于复杂[8]。

4.3 模量代表值与沥青类型关系分析

选取AC-13与AC-16道路石油沥青与SBS、SBR改性沥青混合料，在最佳沥青用量下对比其在不同温度下的模量代表值，结果如图6所示。

由图6可知，AC-13下SBS改性沥青混合料模量代表值在不同温度下均明显高于道路石油沥青与SBR改性沥青混合料，-20 ℃下，相比道路石油沥青，SBS改性沥青混合料模量代表值高出约25%，随着温度的升高，在0 ℃时两种类型下模量基本持平；AC-16在-20 ℃条件下，SBS改性沥青相比道路石油沥青混合料模量代表值高出约11%，在0 ℃及以上条件下相差较小。由此可见，在低温条件下，SBR改性沥青具有较好的延伸性能，混合料弯拉应变较大；SBS改性沥青混合料具有较好的弹性、韧性与较高的抗变形能力，其模量值普遍高于其它类型[9,10]。

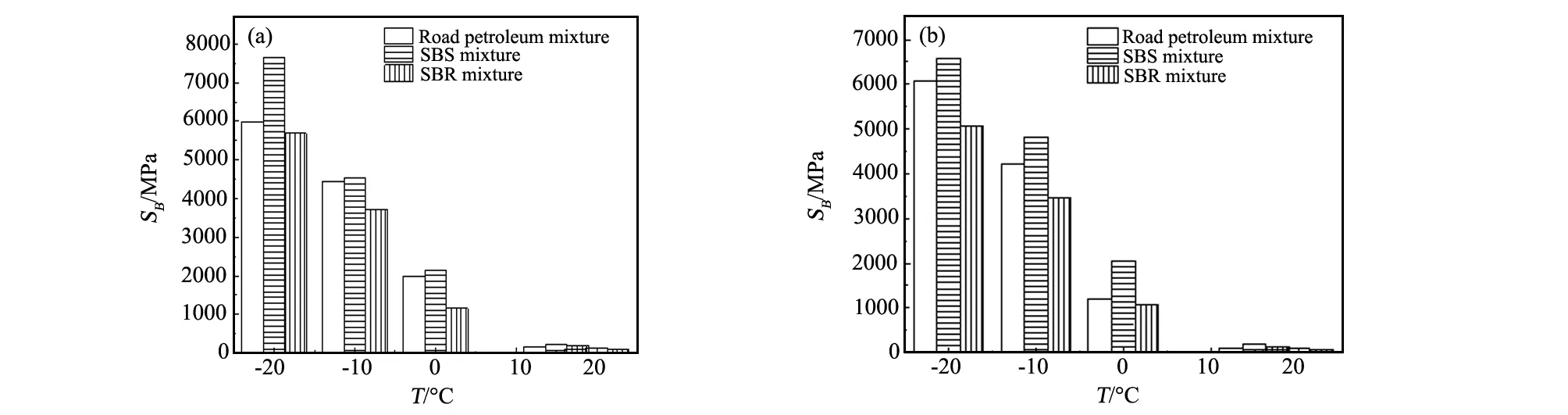
图6 沥青混合料弯曲劲度模量代表值与沥青类型的变化关系(a)AC-13;(b)AC-16Fig.6 Bending stiffness modulus representative value variation versus asphalt types

5 弯曲劲度模量预测模型研究

5.1 基于灰关联理论下的影响因素显著性分析

以上分析了温度、沥青用量与沥青类型对模量代表值的影响，混合料模量代表值随各因素的变化基本符合既有研究中获得的变化关系，表明对大数据进行数学处理获得的模量代表值具有较好的代表性与准确度。为研究各因素对混合料模量影响的显著程度，以便在建立模量预测模型时更合理的选定变量，采用灰关联分析方法对各因素的显著程度进行分析，选取温度作为灰关联分析的参考序列，其余因素作为比较序列。通过灰关联方法对各因素显著程度进行对比。

利用式(2)计算比较序列的所有指标对应于参考序列所有指标的关联系数。

(2)

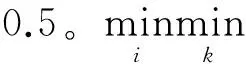
比较序列对应于参考序列的关联度，用平均值表示，如式(3)所示，根据关联度大小进行排序，关联度越大，比较序列与参考序列关系越密切[11]。

(3)

通过灰关联分析理论对各因素显著程度进行对比，结果表明各因素影响显著程度依次为：温度>沥青用量>沥青结合料类型，对比验证灰关联分析结论与第三节中的分析结果，二者结论基本一致，即对于沥青混合料的弯曲劲度模量而言，温度是其首要影响因素，沥青用量与沥青类型次之。

5.2 模量预测模型建立

由于实际工程中多采用沥青混合料马歇尔试件试验确定的最佳沥青用量，因此不再将沥青用量作为变量进行研究。温度是模量的主要影响因素，以温度为变量建立混合料弯曲劲度模量与温度的关系方程，并通过不同的修正系数对粒径、沥青结合料类型进行修正。

以AC-13为例，采用对数模型对混合料弯曲劲度模量代表值与温度的关系进行拟合回归，对道路石油沥青、SBS与SBR改性沥青下的模量代表值取对数，-20 ℃至20 ℃温度范围内的模量代表值与温度关系如图7所示。

弯曲劲度模量与温度的拟合关系式见式(4),混合料弯曲劲度模量拟合方程回归系数及相关系数见表3。

Ln(SB)=L+aT

(4)

式中：SB-弯曲劲度模量，MPa；

T-温度，℃；

L,a-回归系数。

图7 AC-13混合料弯曲劲度模量代表值与温度的关系(a)道路石油沥青混合料;(b)SBS改性沥青混合料;(c)SBR改性沥青混合料Fig.7 AC-13 Bending stiffness modulus representative value variation versus temperature(a)road petroleum asphalt mixture;(b)SBS asphalt mixture;(c)SBR asphalt mixture

表3 方程回归系数及相关系数汇总Table 3 Regression coefficient and Correlation coefficient

由表3可知，不同条件下的回归方程相关系数平方值处于0.89至0.94之间，回归模型具有较好的相关性。在此基础上，对以上预测方程进行修正优化，引入沥青混合料弯曲劲度模量修正系数，以AC-13道路石油沥青混合料模量方程为基准方程，通过混合料粒径修正系数KL与沥青种类修正系数KZ，对不同粒径、沥青种类的混合料模量进行修正。修正后的模量预测方程见式(5)。

Ln(SB)=KLKZ(7.019-0.111T)

(5)

式中：SB-弯曲劲度模量，MPa；

T-温度，℃；

KL-粒径修正系数；

KZ-沥青种类修正系数。

通过反复试算，最终确定AC级配下的粒径修正系数为0.965，SBS改性沥青修正系数为1.037，SBR改性沥青修正系数为0.983，具体汇总结果见表4。

表4 粒径修正系数与沥青类型修正系数汇总Table 4 Particle size correction coefficient and Asphalt type correction coefficient

5.3 模型拟合精度验证

图8 AC混合料弯曲劲度模量模型45°图Fig.8 The 45° figure of bending stiffness modulus model

为验证模型对混合料弯曲劲度模量的拟合效果与适用性，对预测模型获得的弯曲劲度模量预测值与弯曲试验代表值进行对比，绘制各位置处45°等值线图以观察拟合精度。各位置处45°等值线如图8所示。

由图8可知，采用对数模型对混合料弯曲劲度模量随温度的变化进行模拟，模型预测值基本分布于45°等值线附近，可获得较好的拟合效果，具有较高的拟合精度与再现性，有利于对沥青混合料弯曲劲度模量进行预测，为沥青混合料的模量参数取值提供参考。

6 结 论

(1)以沥青混合料弯曲劲度模量为主参数，温度与材料参数为主要影响因素进行数据收集、汇总与筛选，建立了模量数据库;

(2)通过对模量数据库进行处理获得混合料模量代表值，通过对比分析，模量代表值随温度、沥青用量与类型的变化基本符合既有研究中获得的变化关系，采用数学方法处理获得的模量代表值具有较好的代表性与准确度;

(3)建立了适用于沥青混合料弯曲劲度模量预测的对数方程，对弯曲劲度模量代表值与温度的变化关系进行拟合，配合不同的修正系数对模型进行优化，结果表明所建立方程能较好的模拟不同级配、粒径及沥青类型下弯曲劲度模量与温度的关系，具有较高的拟合精度与再现性，有利于较大温度范围内的模量预测与弯拉特性研究，为沥青混合料模量参数取值提供参考。

[1] Wang L Z,Wei J M,Zhang Z.Development of alternative parameters to evaluate the temperature susceptibility of asphalt binders[J].InternationalJournalofPavementResearchandTechnology,2009,2(2):75-81.

[2] 沈金安，李福普，陈 景.高速公路沥青路面早期损坏分析与防治对策[M].北京:人民交通出版社，2004.

[3] 郝培文，张登良，胡西宁.沥青混合料低温抗裂性能评价指标[J].西安公路交通大学学报,2000，03(20)：1-5.

[4] 戴雄威.沥青路面结构的模量取值研究[D].武汉：武汉工程大学，2014.

[5] 申爱琴，蒋庆华.沥青混合料低温抗裂性能评价及影响因素[J].长安大学学报(自然科学版)，2004，05(24)：1-6.

[6] 谭忆秋，李晓琳.温度及荷载频率对沥青-集料交互作用能力的影响[J].中国公路学报，2012，03(25)：65-71.

[7] 马 骉，韦佑坡.高原寒冷地区沥青混合料弯拉特性分析[J].公路交通科技，2010，03(27)：44-49.

[8] 张争奇，王永财.沥青胶浆对沥青混合料高低温性能的影响[J].长安大学学报(自然科学版)，2006，02(26)：1-5.

[9] Lu X H.Fundamental studies on styrene-butadiene-styrene polymer modified road bitumen[J].LicentiateThesisofKUNGLTEKNISKAHOGSKOLANRoyalInstituteofTechnology,19-20.

[10] 谭忆秋，郭 猛，曹丽萍.常用改性剂对沥青粘弹特性的影响[J].中国公路学报，2013，04(26)：7-15.

[11] 曹明霞.灰色关联分析模型及其应用的研究[D].南京：南京航空航天大学，2007.

Value of the Bending Stiffness Modulus of Asphalt Mixture in Surface Layer

TIANYu-xiang,MABiao,ZHOUXue-yan，HUANGWei

(Key Laboratory of Special Area Highway Engineering of Ministry of Education,Chang'an University,Xi'an 710064,China)

The bending stiffness modulus of asphalt mixture is important to the design of asphalt pavement and road performance evaluation, especially for the surface layer of asphalt mixture, the size of the modulus is closely related to the material mechanics performance. However, at present, there is lack of the study on the understanding of the reasonable value of modulus in pavement structure design and analysis. This paper established the database of modulus by collecting the existed module data; using proper mathematical processing to acquire the modulus representative value in different condition. The comparative analysis results show that the change relationship between temperature, asphalt content, asphalt type and representative value is basically in line with the existing research conclusions, the representative value had good veracity and representation; gave the modulus prediction equation by fitting regression method, through validated methods, the polynomial curve built has high fitting accuracy and reproducibility, which can provide reference for the value of modulus in asphalt pavement structure design and analysis.

bending stiffness modulus;representative value;temperature;material parameters;prediction model

“十二五”国家科技支撑计划(2014BAG05B04);交通运输部建设科技项目(2013-318-490-010)

田宇翔(1990-)，男，博士研究生.主要从事路面结构与材料的研究.

U414

A

1001-1625(2016)10-3280-08