基于改进灰色理论的中长期负荷预测方法研究

刘宇，郭林，阳锋，江登笠，任铃，李君

（1.国网四川省电力公司德阳供电公司，四川德阳 618000；2.国网四川省电力公司发展策划部，四川成都 610041；3.国网四川省电力公司阿坝供电公司，四川茂县 623200）

基于改进灰色理论的中长期负荷预测方法研究

刘宇1，郭林2，阳锋3，江登笠1，任铃1，李君1

（1.国网四川省电力公司德阳供电公司，四川德阳 618000；2.国网四川省电力公司发展策划部，四川成都 610041；3.国网四川省电力公司阿坝供电公司，四川茂县 623200）

中长期负荷预测是配电网规划的必要前提，对于电力系统经济效益和社会效益的提升具有重要意义。针对传统灰色预测模型预测精度低，适用性不强的缺陷，提出了一种基于改进灰色理论的电力系统中长期负荷预测方法。该方法在经典灰色预测GM（1，1）模型的基础上，首先利用三点平滑法对历史数据进行预处理，然后再构建基于等维新息矩阵的GM（1，1）模型，最后利用残差处理方法对预测结果进行修正。基于四川某地区售电量负荷预测的实际算例的仿真结果表明，相比于传统灰色预测模型，本文提出的改进灰色预测方法在预测精度和适用性方面都具有显著优势。

中长期负荷预测；灰色预测；三点平滑法；等维新息；残差处理

随着我国“全球互联网”战略和“可再生能源”发展战略的逐步推进，电力系统规划的精细化要求也日益提升。中长期负荷预测不仅能为电力系统经济安全运行提供有效的保障，而且能为科学合理的进行电力系统规划提供可靠的数据支撑。因此，具有更高精度和适用性的中长期负荷预测方法[1-2]研究已成为近年来人们的研究热点。

中长期负荷预测具有预测样本少，时间跨度大，影响因素多等特点，如何在众多的预测方法中选择合适的预测模型，在提高其预测精度的基础上，增强其普遍适用性，是中长期负荷预测的难点。目前，中长期负荷预测方法可以分为传统预测方法和新兴预测方法2类[3]。传统的预测方法一般是从历史数据中挖掘电量和电力负荷随相关因素的变化规律，然后构建一种确定性的数学模型来描述上述变化。由于影响电力系统负荷的因素众多，其变化规律复杂且具有不确定性，仅以一种确定的模型显然难以准确描述负荷的变化规律。如趋势外推法[4]，常利用指数函数、线性模型、包络曲线等一些比较简单的数学函数模型，描述负荷变化随时间增长的恒定变化趋势，虽然简单方便，但难以拟合负荷变化趋势的多样性；指数平滑法[4-5]通过计算指数平滑值，利用一次、二次或者三次指数平滑法固有的预测公式进行负荷预测，预测精度较差；回归分析法[6]利用线性回归模型或者非线性回归模型对历史负荷数据进行统计分析，从而实现对未来负荷数据的预测，但数学模型对数据本身的信息过于依赖，且求解非线性回归预测模型过程太复杂。伴随着新兴学科的不断兴起和人工智能技术的不断完善，近年来涌现了一批新兴的负荷预测方法，这类方法从负荷的历史数据特性出发，挖掘其内在数学特征，并基于数据对所建模型进行实时修正，从而有效避免了采用单一确定模型描述负荷变化趋势的弊端，具有明显优势。文献[7]所采用的模糊预测法是利用模糊数学的概念来描述大系统中的一些复杂现象，在进行负荷预测时可以有效的处理负荷变化的不确定性，预测结果可靠性较高，但通常对历史数据规模要求较为苛刻；文献[8]所使用的神经网络法，通过模拟人脑神经系统具有较强学习能力的特点，利用历史数据训练出负荷模型，然后再利用该模型进行负荷预测，虽然具有较强的自学习和自适应能力，但这种方法仅适用于样本空间巨大的短期负荷预测；文献[9]所提出的传统的灰色预测方法和文献[7]中的模糊预测法类似，它把模糊控制的观点和方法延生到电力系统中，将复杂电力系统中的各种不确定性因素模糊化处理，等效成一个灰度空间，所不同的是传统的灰色GM（1，1）模型所需历史数据较少，不需要考虑分布规律和变化趋势，模型简单易于实现，被认为是最适用于中长期负荷预测的有效方法之一。

传统灰色预测模型虽然在中长期负荷预测方面较其他方法具有显著优势，但是预测精度会随着数据灰度的增大而出现较为明显的下降，并且适用性不强。文献[10]和文献[11]分别利用粒子群算法和神经网络算法对GM（1，1）模型中的发展系数和协调系数进行求解，虽然能在一定程度上提高预测精度，但是在提高模型的适用性方面效果并不显著。文献[12]提出了通过等间隔处理原始数据和背景值改造的改进方法，虽然在预测精度和模型的适用性上都有所提高，但是忽略了数据本身信息对预测过程的影响，对于时间较远的负荷，预测精度得不到保证。

综上所述，本文提出了一种基于改进灰色预测的中长期负荷预测方法，通过对模型原始数据进行预处理，降低原始数据奇异点对预测精度的负面影响；同时在传统GM（1，1）模型的基础上，构建等维新息模型，引入新陈代谢特征，保证数据模型的“年轻化”，提升模型的普适性和对远端预测点的预测精度；最后对预测结果进行局部残差修正，进一步减小了模型的预测误差。基于四川某县实际数据的仿真结果表明，相比于传统灰色预测模型，本文提出的等维新息残差GM（1，1）预测模型在预测精度和适用性方面都具有显著优势。

1 灰色系统的GM（1，1）模型

GM（1，1）模型是由一个只包含单变量的一阶微分方程构成的模型，首先通过对自身数据模型进行累加处理，生成有规律的指数序列，然后利用新数列进行建模求解，实质上就是利用差分方程反演微分方程的过程。其具体过程如下：

GM（1，1）模型的基本形式为

已知原始非负数列X（0）：

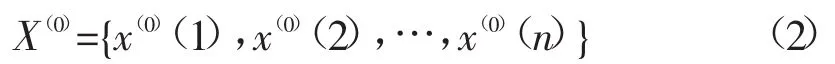
对数列X（0）进行累加迭代，得到数列X（1）：

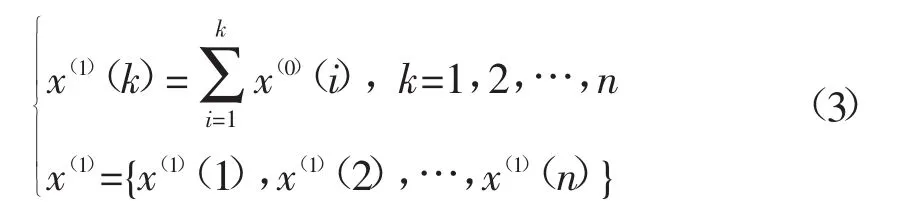
X（1）的近邻均值生成为Z（1）：

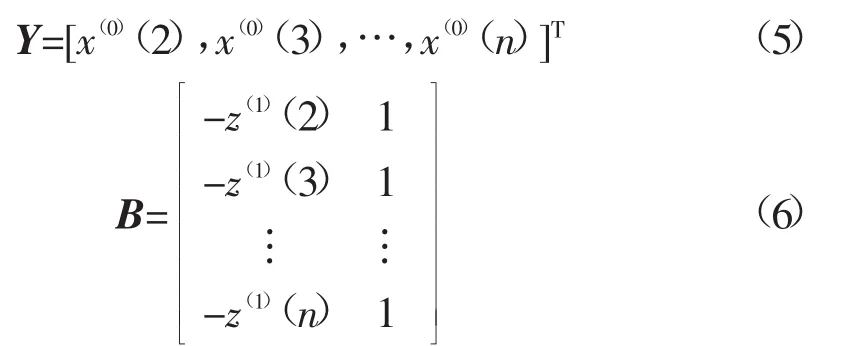
利用最小二乘法求解出模型参数A：

X（1）为X（0）的一次累加生成序列（1-AGO），Z（1）为X（1）的近邻值序列，利用X（1）建立方程（1）的一阶白化线性微分方程：

式中：a为模型的发展系数，它主要是反应X（1）的发展趋势；u为模型的协调系数，它反应了数据间的变化关系。

得到上述白化微分方程（8）的时间响应方程为：

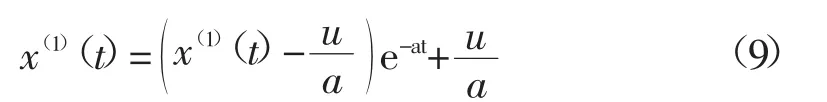
GM（1，1）模型（1）的时间响应序列为：

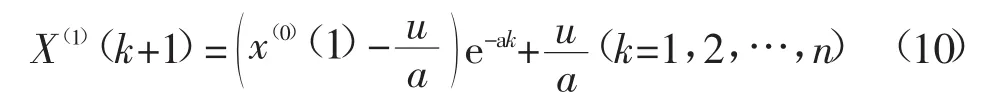
对上式进行累减还原生成，得到X（0）的预测模型为：

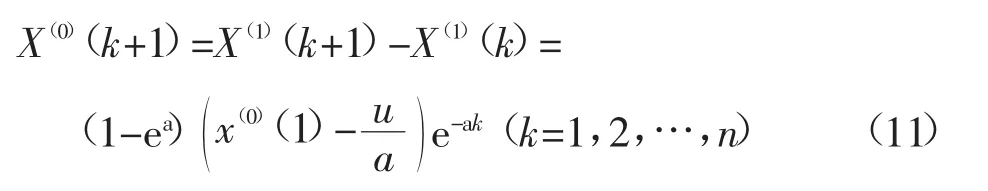
2 GM（1，1）模型原始数据的预处理

GM（1，1）模型基于实际的历史负荷数据进行预测，但一般情况下实际负荷数据会受人为因素，随机突发事件等多方面因素的影响，这必将导致实际测量值与正常情况下的平均负荷值产生异常。奇异值会严重干扰原始数据本身规律变化趋势，使模型对数据列的变化产生误判，预测结果的精确性会受到影响。针对上述问题，本文采用了三点平滑法对原始负荷数据进行预处理。

2.1 三点平滑法

三点平滑法就是通过重新分配待处理数据和前后数据的权值，加强待处理数据的权重，减小数值的波动性，增强待处理数据与前后数据的联系的数据处理方法。具体过程如下：

已知原始非负数列X（0）（k）

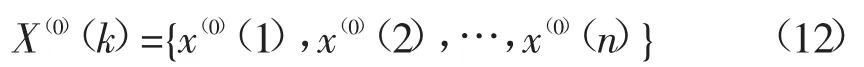
平滑处理位于数列中间（除开x（0）（1）和x（0）（n））的数据：

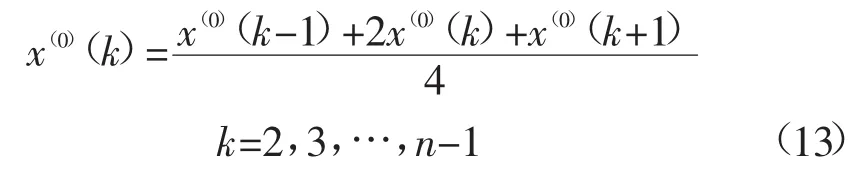
而对数列两端数据平滑处理的计算公式为：

选取四川某地区某2条低压线路①和线路②2004—2009年一月份售电量负荷数据进行平滑处理如表1所示。

表1 线路①原始负荷处理Tab.1 Original load processing of line① MW

表2 线路②原始负荷处理Tab.2 Original load processing of line② MW

由表1、表2可以发现，采用三点平滑法处理后的数据组波动性更小，规律性更强，更加适合建立数学模型。

3 GM（1，1）模型的改进措施

为了进一步提高模型的预测精度和普适性，本文提出了一种建立等维新息预测模型和对预测结果进行局部残差检验的综合改进措施。

3.1 等维新息预测模型

电力系统是一个大的灰色系统[13]。传统灰色模型虽然可以作为长期负荷预测模型对未来的负荷变化趋势做出一定的预测，但随着电力系统的不断发展，各种新设备的不断接入，电力系统将不断地受到一些新的干扰因素的影响，模型预测结果真正具有实际意义、精度较高的往往是前几个数据，随着时间的推移，原始GM（1，1）模型计算的预测数据，其预测意义就越小。同时原始的GM（1，1）模型往往完全利用原始历史负荷数据组的整体或局部变化规律进行预测，但往往建模历史负荷越久远，负荷本身所携带的信息对预测过程所做出的贡献就越少，这样就导致预测精度就会越小，意义也就越小，模型的适用性将会受到很大的影响。针对传统灰色模型以上两点局限性，采用建立等维新息GM（1，1）模型的手段进行改进。

选取建模数据如

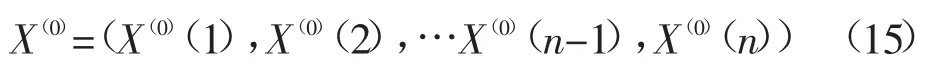
以原始模型实时预测出的最新的数据作为新模型建模数据组的新增项，然后去掉最老的数据，得到如（16）新的建模的数列。

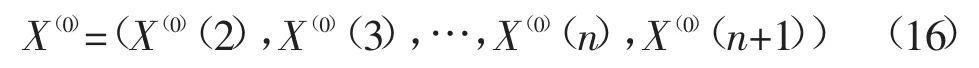
依照上述数列更新方法，每次建模数据都利用最新预测的数据来替换掉最老的数据，保持数列等维，依次推进，使建模数列不断新陈代谢，自我更新，保持数列“年轻化”，直至完成预测目标为止。

3.2 局部残差处理

通过局部残差处理[14]对等维模型预测结果进行修误差正，更一步提高模型预测精度。残差处理过程如下：

设一组预测值为：

残差项定义为：

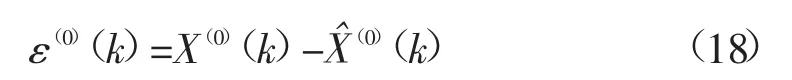
生成残差数列：

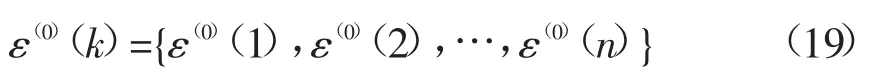
取k=m，m+1，…，n（m＞1），生成局部残差序列：

累减还原生成残差预测值模型：

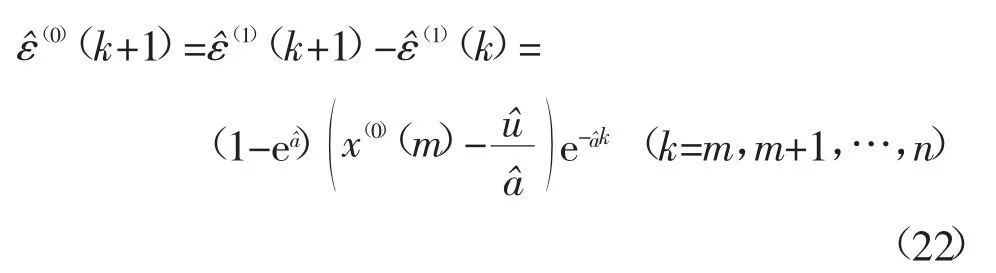
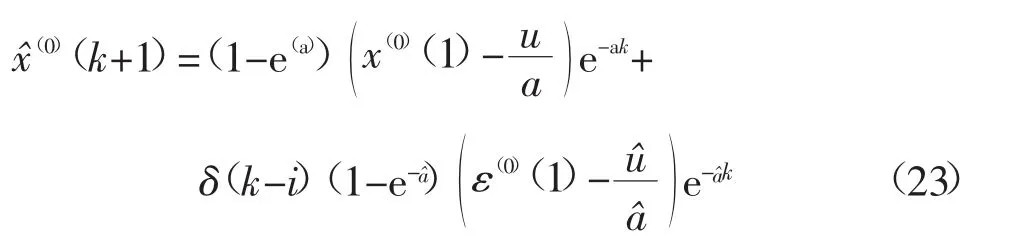
4 算例分析

4.1 算法

本文采用最小二乘法对模型的发展系数a和模型的协调系数u进行求解。其具体求解原理如下：

考虑超定方程组：

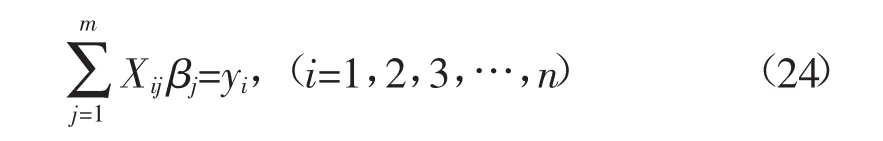
式中：m为有m个未知数β；n为有n个等式，m＜n，将上式量化后为：

引入残差平方和函数S：

对S（β）求最值可以得到：

如果矩阵XTX非奇异，则β有唯一解。

根据上述步骤可以求得本文所需要的一阶白化线性微分方程的模型参数如式（7）所示。

4.2 算例仿真

本文以四川某地区电网2004—2015年历史实测售电量数据为基础，仿真实验在Matlab环境下编程实现。

利用如表1、表2所示的2004—2009年不同线路的预处理前后的历史负荷数据为样本建立数学模型，分别以传统的GM（1，1）模型，等维新息GM（1，1）模型和等维残差GM（1，1）模型对四川某地区线路①和线路②2010年—2015年的一月份售电量负荷进行预测并进行误差分析。预测结果如表3、表4所示，得到线路①、线路②不同模型相对误差对比柱状图如图1，图2所示。

由表3可知，传统模型大部分预测误差值大于15%，而改进模型后预测结果相对误差明显降低，大部分位于15%以下，预测效果得到明显好转。可以发现，相比于传统模型，本文所提出的等维残差模型具有更好的预测精度。

由表4、图1、图2可知，相比于直接利用原始数据建模，经过数据预处理后，预测相对误差明显降低，预测效果得到明显改善。

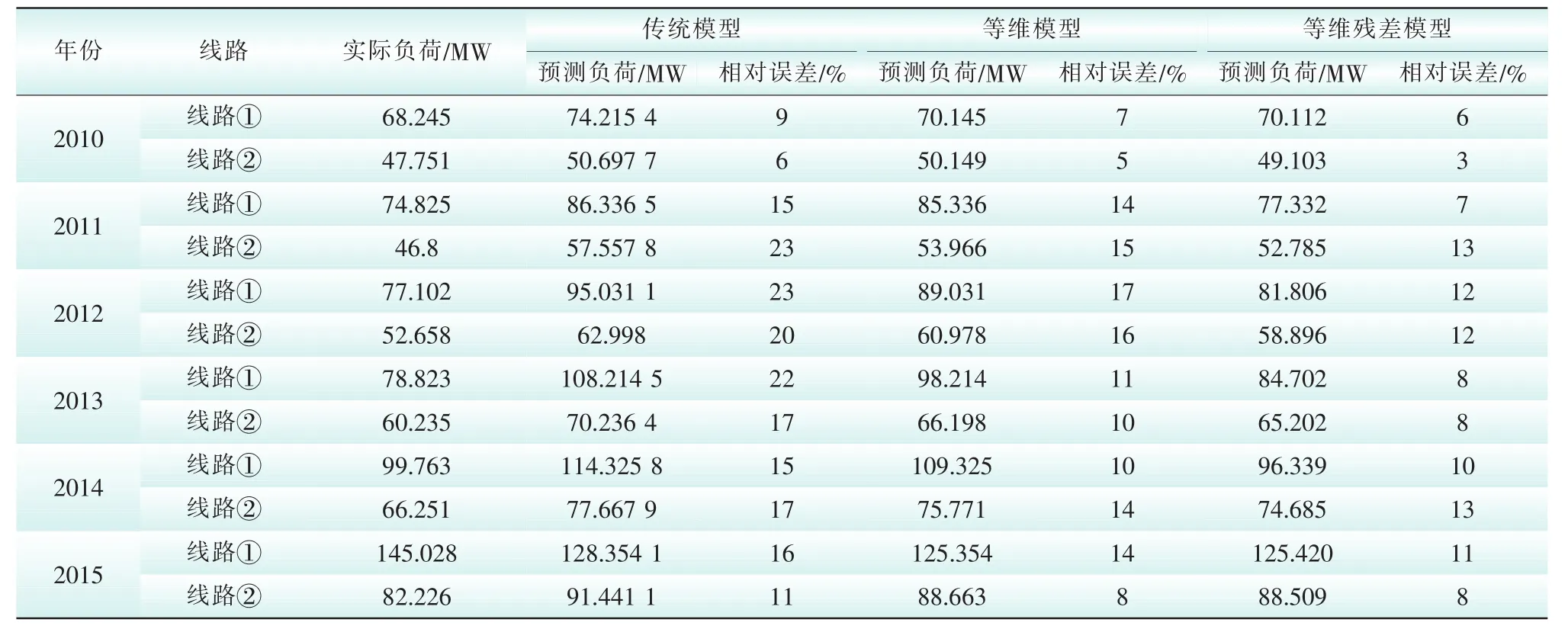
表3 不同模型预测结果（数据处理前）Tab.3 Different model predictions（no data pre-processing）

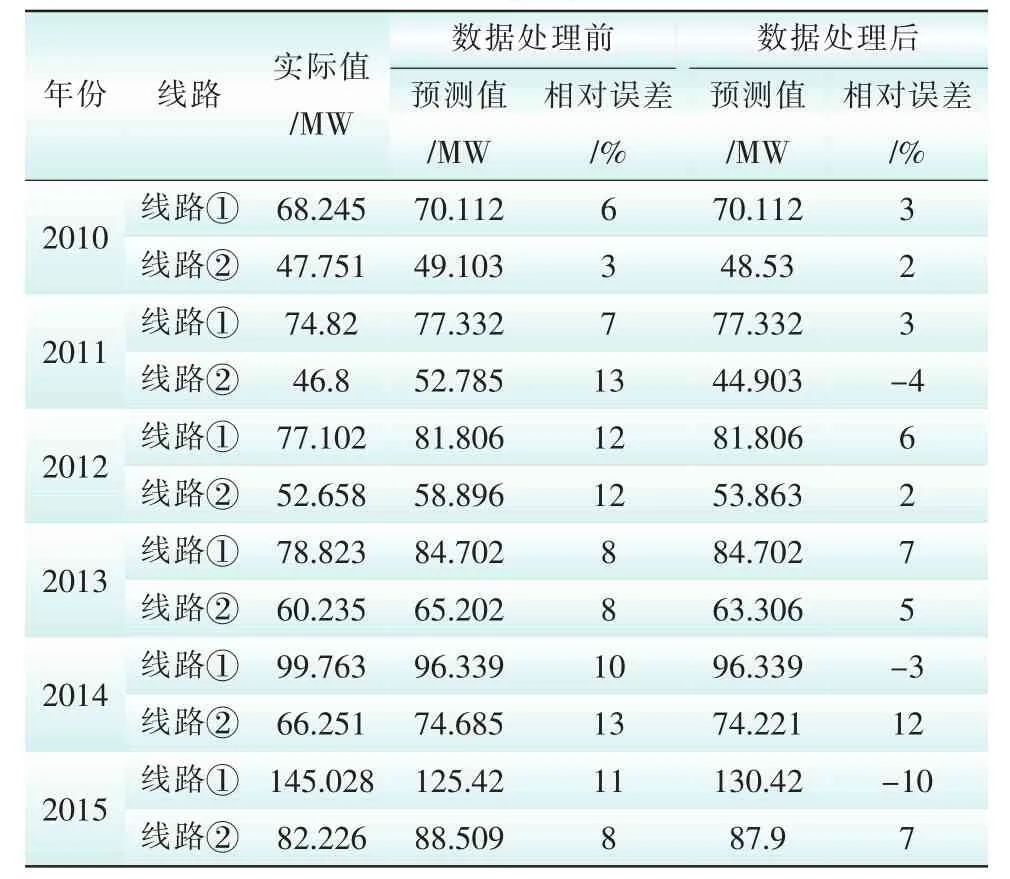
表4 改进模型数据预处理前后预测结果Tab.4 The improved model predictions before and after the data preprocessing

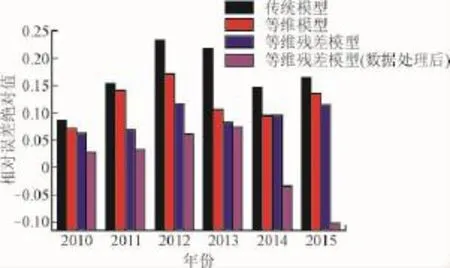
图1 线路①预测相对误差对比柱状图Fig.1 The contrast histogram of the prediction relative errors of line①

图2 线路②预测相对误差对比柱状图Fig.2 The contrast histogram of the prediction relative errors of line②

针对该地区30条同等级线路，分别以传统的GM（1，1，）模型、文献[10]中粒子群优化灰色模型和本文改进的等维残差GM（1，1）模型对其2015年不同月份负荷量进行负荷预测，通过误差处理分别得到模型改进前后的误差概率密度，然后利用高斯函数对不同模型预测误差概率密度进行拟合得到如图3所示的对比拟合曲线。

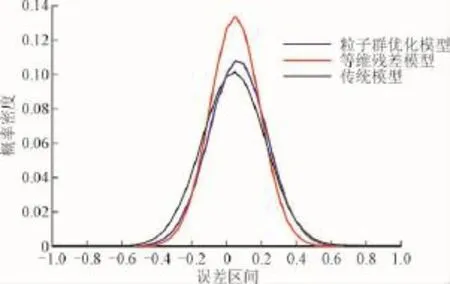
图3 不同模型预测误差概率密度对比拟合曲线Fig.3 Probability density curve of the different models' prediction errors

由图3中传统模型预测概率密度曲线（图3中黑色曲线）可以发现，利用此模型进行负荷预测，误差大部分集中于误差区间[－0.4，0.4]，但还有不少误差值位于误差区间[－0.6，－0.4]和[0.4，0.6]，整体预测效果欠佳，预测精度还需进一步提升。

而图3中粒子群优化模型预测概率密度曲线（图中蓝色曲线），整体预测效果和传统GM（1，1）模型相比相差无几。由此可以发现文献[10]所提出的粒子群优化模型在针对不同对象和不同时间段大量预测样本时，其适用性没有得到改善。

如图3中所示改进的等维残差模型的预测误差概率密度曲线（图中红色曲线），相比于另外两种模型而言，其预测误差位于区间[－0.4，0.4]的概率密度明显增大，在针对不同对象和不同时间段大量预测样本时，其预测效果得到较为明显的改善，由此可以看出，本文所提出的改进等维残差灰色模型在提高了模型预测精度的基础上，其适用性也得到了明显的改善。

5 结论

针对传统的GM（1，1）模型的精度低，普适性差等局限，本文提出了等维残差灰色GM（1，1）改进预测模型。在Matlab仿真环境，将改进模型用于对四川某地区负荷量进行仿真预测，仿真效果有效的验证了改进模型与传统的GM（1，1）模型相比，在预测精度和适用性有着明显的改善。

[1]柴淑云.电力系统中长期负荷预测方法的研究与软件开发[D].北京：华北电力大学，2006.

[2]金鑫，罗滇生，孙广强，等.中长期电力负荷预测模型筛选与组合方法[J].电力系统及其自动化学报，2012，24（4）:150-156.JIN Xin，LUO Diansheng，SUN Guangqiang，et al，Sifting and combination method of medium and long-term load forecasting model[J].Proceedings of the CSU-EPSA，2012，24（4）:150-156（in Chinese）.

[3]廉巍巍.电力系统中长期负荷预测模型的研究[D].太原：太原理工大学，2007.

[4]周潮，邢文洋，李宇龙.电力系统负荷预测方法综述[J].电源学报，2012（6）:32-39.ZHOU Chao，XING Wenyang，LI Yulong.A review of powersystem load forecasting methods[J].Journalof Electric Power，2012（6）:32-39（in Chinese）.

[5]齐驰，侯忠生.自适应单指数平滑法在短期交通流预测中的应用[J].控制理论与应用，2012，29（4）:465-469.QI Chi，HOU Zhongsheng.Application of adaptive singleexponent smoothing for short-term traffic flow prediction[J].Control Theory and Application，2012，29（4）:465-469（in Chinese）.

[6]王勇，黄国兴，彭道刚.带反馈的多元线性回归法在电力负荷预测中的应用[J].计算机应用与软件，2008，25（1）:82-84.WANG Yong，HUANG Guoxing，PENG Daogang.Application of multiple linear-feedback regression analysis to electric load forecasting[J].Computer Applications and Software，2008，25（1）:82-84（in Chinese）.

[7]严华，吴捷，马志强，等.模糊集理论在电力系统短期负荷预测中的应用[J].电力系统自动化，2000，24（11）: 67-72.YAN Hua，WU Jie，MA Zhiqiang，et al.Application of fuzzy set theory to short-term load forecasting in power system[J].Automation of Electric Power Systems，2000，24（11）:67-72（in Chinese）.

[8]黄湘君.基于主成分分析的BP神经网络在电力系统负荷预测中的应用[J].科技信息，2008（16）:313-314.HUANG Xiangjun.Application of BP neural network in power system load forecasting based on principal component analysis[J].Science and Technology Information，2008（16）:313-314（in Chinese）.

[9]蔡琼，陈萍.灰色GM（1，1）模型及其在电力负荷预测中的应用[J].自动化技术与应用，2006，25（3）:24-26.CAI Qiong，CHEN Ping.Grey GM（1，1）model and its application in power load forecasting[J].Automation Technology and Application，2006，25（3）:24-26（in Chinese）.

[10]吴昌友，王福林，董志贵，等.改进粒子群优化算法在电力负荷组合预测模型中的应用[J].电网技术，2009（2）:27-30.WU Changyou，WANG Fulin，DONG Zhigui，et al.Application of improved particle swarm optimization in power load combination forecasting model[J].PowerSystem Technology，2009（2）:27-30（in Chinese）.

[11]黄元生，贾春燕.基于粒子群算法和BP神经网络改进的灰色电力负荷预测研究[J].国网技术学院学报，2014（5）:6-11.HUANG Yuansheng，JIA Chunyan.Grey power load forecasting based on particle swarm optimization and BP neuralnetwork[J].JournalofState Grid Technology College，2014（5）:6-11（in Chinese）.

[12]赵文清，王飞.基于改进型灰色理论的中长期电力负荷预测模型[J].东北电力技术，2011，32（7）:46-48.ZHAO Wenqing，WANG Fei.Prediction model for Medium and Long-term electric load based on improved grey theory[J].Northeast Electric Power Technology，2011，32（7）:46-48（in Chinese）.

[13]邓聚龙.灰色理论基础[M].武汉：华中科技大学出版社，2002.

[14]马晓光，孟伟.残差修正法在电力负荷预测中的应用[J].电网技术，2001，25（4）:21-23.MA Xiaoguang，MENG Wei.Application of residual error amendment method in power load forecasting[J].Power System Technology，2001，25（4）:21-23（in Chinese）.

郭 林（1973—），通信作者，男，高级工程师，主要研究方向为配电网规划。

（编辑 李沈）

Medium and Long Term Load Forecasting Based on Improved Gray Theory

LIU Yu1，GUO Lin2，YANG Feng3，JIANG Dengli1，REN Ling1，LI Jun1
（1.State Grid Deyang Power Supply Company，Deyang 618000，Sichuan，China；2.Department of Development Planning，State Grid Sichuan Electric Power Company，Chengdu 610041，Sichuan，China；3.State Grid Aba Power Supply Company，State Grid Sichuan Electric Power Company，Maoxian 623200，Sichuan，China）

Medium and long term load forecasting is a necessary precondition of distribution network planning，and has important significance for the improvement of the economic benefitof the power system and social benefit.In view of shortcomings of the traditional grey forecasting model with low precision and low applicability，a new method based on Improved Grey Theory for long term load forecasting in the power system is presented.First，this method uses the threepoint smoothing method to pre-process historical data，and then builds a model of GM（1，1）based on a matrix of equal dimension and new information.Finally the residual method is used to correct the prediction results.The simulation based on the load forecasting of a region in Sichuan shows that compared with the traditional gray forecasting model，the improved grey forecasting method proposed in this paper has obvious advantages in terms of prediction accuracy and applicability.

medium and long term load forecasting；gray forecasting；three point smoothing method；equal dimension and new information；residual processing

国家自然科学基金项目（51477121）。

Project Supported by National Natural Science Foundation of China（51477121）.

1674-3814（2016）08-0051-06

TM715

A

2015-12-23。

刘 宇（1980—），男，高级工程师，主要研究方向为电网规划和投资计划；