蒸汽动力系统设计与多周期运行同步优化
于明欣,董克林,张锋镝
(大连西太平洋石油化工有限公司,辽宁 大连 116600)
生产技术
蒸汽动力系统设计与多周期运行同步优化
于明欣,董克林,张锋镝
(大连西太平洋石油化工有限公司,辽宁 大连 116600)
蒸汽动力系统(Steam power system,SPS)是炼油企业的重要组成部分,针对炼油企业蒸汽动力系统设计与运行方案上存在的不合理方面,通过对蒸汽动力系统建立混合整数线性优化模型(MILP),改善部分系统结构、调整系统多周期运行方案,从而降低蒸汽动力系统的运行费用实现系统的优化。以某炼油企业蒸汽动力系统实为背景,对企业蒸汽动力系统的设计与多周期生产调度方案进行优化,并验证优化策略的有效性。
炼油企业;蒸汽动力系统;优化;MILP
炼油企业的蒸汽动力系统的合理设计与经济运行是国内外研究人员研究的重点。Nishio等[1]用启发式方法,设计出生产工艺用气的蒸汽动力系统,并应用此方法对实际系统进行优化,提高力系统的热效率。Grossmann等[2]应用混合整数线性规划(MILP)方法对蒸汽、电力需求量稳定的系统进行多周期运行参数和设备布局的同步优化。Grossmamm等[3]设计出一种普遍适用的混合整数线性规划方法对系统进行集成建模。Chen等[4]提出蒸汽分配网络的概念,在考虑生产过程用气量的同时对蒸汽动力系统的结构进行柔性设计。盖丽梅[5]考虑不确定因素的优化策略能避免基于确定性设计策略的保守设计,针对不确定因素的实现提出相应的调度调节策略。
本文同时考虑蒸汽动力系统最优设计和优化运行,构建混合整数线性模型,并加入设备启停费用。结合工程实例进行了优化研究。
1 蒸汽动力系统优化模型
1.1 通用模型
1.1.1 物料平衡
设备n(n={1,2,…,N})在周期t的所有物料流入量等于所有物料的流出量之和,如式(1)所示,式中n表示蒸汽动力系统中的设备或集汽联箱,i表示流入设备n的第i种物流,j表示流出设备n的第j种物流,F表示其相应流量。

(1)
1.1.2 能量平衡
设备n在周期t的所有供给能量之和等于流出能量之和,如式(2)所示。式中H表示周期t流入或流出设备n的物料焓值,Q表示外界提供给装置n的热能。

(2)
1.1.3 操作约束
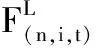

(3)
Zn,t≥Yn,t-1-Yn,t,∀n∈N, t∈T
(4)
Zn,t≥Yn,t-Yn,t-1,∀n∈N, t∈T
(5)
Zn,t≤Yn,t-1+Yn,t,∀n∈N, t∈T
(6)
Zn,t≤2-Yn,t-1-Yn,t,∀n∈N, t∈T
(7)
式中,Zn,t用来表征相比于周期t-1(t={2,3,…,T}),设备n在周期t是否发生运行状态的改变。当设备前一周期与本周期的启停状态不一致,则Zn,t为1,反之为0。
1.2 装置约束
1.2.1 锅炉
以锅炉的热动力学原理为基础,Shang等[6]由锅炉的效率公式推导出锅炉的线性能量模型,如式(8)所示。
∀fuel∈FUEL, boiler∈BOILER, t∈T
(8)
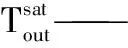
Fstm,boiler,t——锅炉boiler在周期t的蒸汽流量,t
1.2.2 汽轮机
汽轮机将蕴含在高温高压蒸汽中的热能转化为机械能或电能。实际生产中,改变汽轮机的抽汽量是调节蒸汽管网中不同等级蒸汽平衡的重要手段之一。Shang等[6]改进了背压式汽轮机的数学模型,提高了模型的精度,如式(9)所示。
∀turb∈TURB, t∈T
(9)

1.3 供需约束

∀stm∈STM, t∈T
(10)
Eturb,t=Ddrv,t
∀turb∈DTURB, drv∈DRIVE, t∈T
(11)
∀turb∈ETURB, t∈T
(12)
0Elenet,t,∀t∈T
(13)
1.4 目标函数
蒸汽动力系统运行优化的目标是,根据产能和耗能设备的运行参数、能源管网内部不同公用工程的产耗平衡,建立混合整数线性规划模型,通过模型求解,获得兼顾生产成本和生产需求的系统设计和多周期运行同步优化。生产成本如式(14)所示,其中包括产能设备燃料成本、新鲜水的成本、外购电力成本以及设备的启停成本。
(14)
其中,fuel表示产能设备所用的燃料,如燃料油或者燃料气,Cfuel为燃料的单价,Cwat为新鲜水的单价,Cele为外购电力的单价,Cch_bl表示锅炉设备的启停成本,Cch_tb表示汽轮机设备的启停成本。
2 实 例
此算例是对蒸汽动力系统设计与运行的同步优化,图1为某石化企业蒸汽动力系统的初期设计超结构流程图。根据该石化企业蒸汽电力的需求量,拟设计1台高压CFB锅炉B1、1台中压CFB锅炉B2、6台背压汽轮机T1~T6和3个减温减压器。其中两台锅炉的额定蒸发量分别为220 t/h、130 t/h,6台汽轮机的额定功率均为12 MW,设计初期主要设备参数见表1和表2。蒸汽动力系统初始设计的超结构由4个等级的蒸汽管网组成,这4个管网的压力分别是9.9 MPa、2.35 MPa、2.07 MPa和0.34 MPa,具体参数见表3。
各周期工艺生产对各个压力等级蒸汽、动力的需求量如表4所列出。对拟设计的系统超结构集成建模,通过多周期的模拟运行设计出既能满足企业蒸汽、动力需求,又能使全周期总运行费用最低的蒸汽动力系统。本文研究的多周期模型分为12个连续生产周期,每周期为1个月。主要对系统结构、生产费用和设备启停方面的研究。该案例使用GAMS 24.2.2 建立混合整数线性规划模型,并采用CPLEX 求解器,计算环境为Intel(R)Core(TM)i5-5200U CPU@2.20GHz。目标函数优化求解时间为0.724 s。

表1 锅炉参数

表2 汽轮机运行参数表

图1 蒸汽动力系统流程图

项目焓/(kJ/kg)压力/MPa温度/℃超高压蒸汽347399540高压蒸汽3219235390中压蒸汽3146207250低压蒸汽2743034139

表4 各等级蒸汽需求量
2.1 生产成本
初始设计系统需要购买超高压蒸汽和电力,外购电力价格0.50元/kWh,外购高压蒸汽价格150元/t、煤价格220元/t(低位发热量24000 kJ/kg)、工业用水3.5元/t。
2.2 优化结果分析
优化后得到的蒸汽动力系统超结构流程图见图2。全周期系统总费用为1.13 亿人民币,工艺生产所需的蒸汽都可以由超高压锅炉提供,不需要再购买蒸汽,为企业节约了大量成本。因为该石化企业生产的电力只能由企业内部消化,暂时不能向国家电网输送,所以企业要尽量控制发电量,不足的电量可以从国家电网上购买。经过对上面初始设计的蒸汽动力系统超结构模型优化后,超结构的设备组成已基本确定。从优化结果中我们能够看出,1台超高压锅炉和4台背压式透平便可以满足该企业的蒸汽和电力的需求,中压锅炉和另外3台机轮机可以弃用。大量的高温高压蒸汽通过透平到达低压管道中为工艺生产提供能量,从减温减压器流过的蒸汽量很少。锅炉、汽轮机的实际运行情况都基本达到了设计工况,所以设备的运行效率得到了保障。

图2 优化后的蒸汽动力系统流程图

项目B1蒸发量/(t/h)B1燃料量/(t/h)T1进气量/(t/h)T1输出功/kWT3进气量/(t/h)T3输出功/kWT4进气量/(t/h)T4输出功/kWT6进气量/(t/h)T6输出功/kW阀1流量/(t/h)阀2流量/(t/h)阀3流量/(t/h)外购蒸汽/kW外购动力/kW周期11802536111466291474932800131990319524200217931918842098102800周期216521339251522193575193301524985143227512464080000624000周期31501832903751009054498839238286209523216287983833201064100周期415018321053659468146537547716562686182999268574615122554400周期5153188976084294555608909823706601184310827838000000周期61652133107686077865768935682732443213176815832200001419200周期716020239805553449580594173319551826818051616660000521600周期8158199091065139995606909464734767972260623340700001394466周期9158199096215430725621911913219522192262123475800001503266周期101602023107136046865713926772287371011171315340400001283200周期11158199085864846365586906183254527917308627637500001587266周期12170225310680602849568092149332053851316801504890000835200
从本模型的优化结果表5中还可以看出,锅炉和汽轮机不存在启停问题,只有减温减压器有个别周期的启停,这样可以减少全周期的总费用。运行优化后设备的运行情况如表6所示。
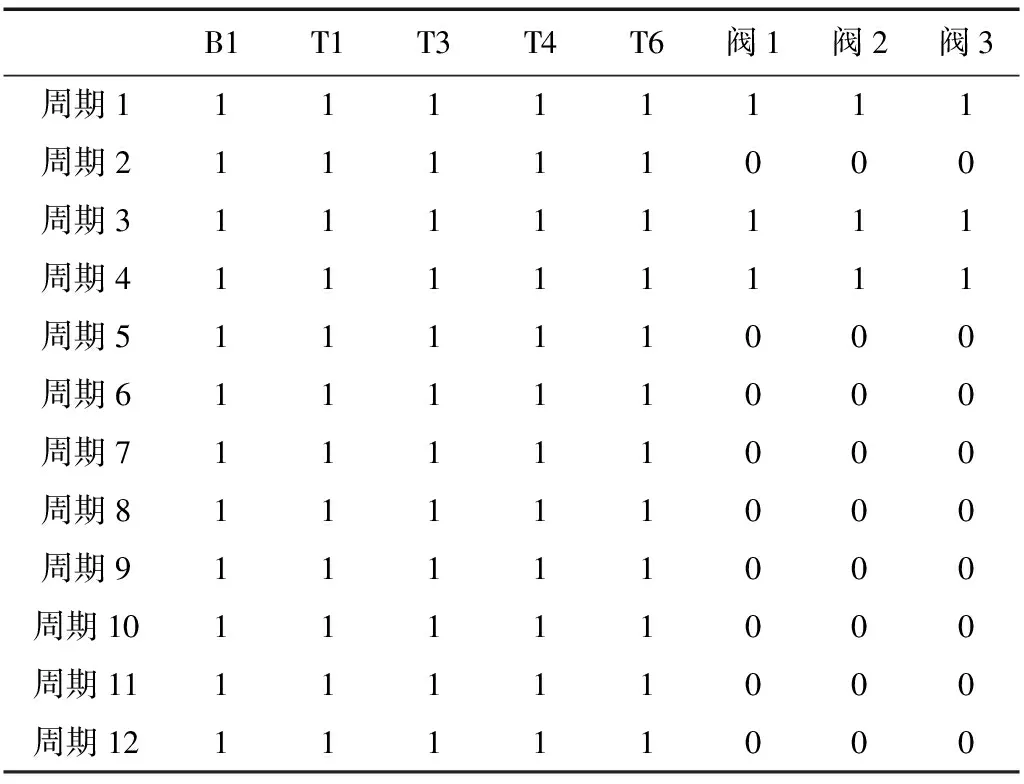
表6 运行优化后的设备状态
3 结 论
以往在设计蒸汽动力系统时,基本都是分别考虑设计与运行问题,这种做法通常会导致设计与运行的脱节。本文将对设计与运行同步优化:首先根据生产要求选好设备种类;依据经验构建一个初始的蒸汽动力系统超结构;在运用混合整数非线性规划(MINLP)对模型进行优化计算,确定设备的取舍和结构的调整。通过这种方法既能完成对系统的设计,同时又对系统进行了优化,可以满足热功需求的目标,为企业减少了不必要的浪费,控制了全周期的总费用。
[1] Nishio M, Itoh J, Shiroko K, et al. A Thermodynamic Approach to Steam-Power System Design[J].Industrial & Engineering Chemistry Process Design & Development, 1980, 19(2):306-312.
[2] Papoulias S A, Grossmann I E. A structural optimization approach in process synthesis—I: Utility Systems [J]. Computers & Chemical Engineering, 1983, 7(6):707-721.
[3] Iyer R R, Grossmann I E. Optimal multiperiod operational planning for utility systems[J]. Computers & Chemical Engineering, 1997, 21(8):787-800.
[4] Chen C, Lin C. A flexible structural and operational design of steam systems [J]. Applied Thermal Engineering, 2011, 31(13):2084-2093.
[5] 盖丽梅,孙力,刘畅,等.基于带补偿随机规划的蒸汽动力系统优化设计[J].化工学报, 2014(11):4509-4516.
[6] Shang Z, Kokossis A. A transhipment model for the optimization of steam levels of total site utility system for multi-period operation[J]. Computers & Chemical Engineering, 2004, 28(9):1673-1688.
Simultaneous Optimization for Design and Operation of Steam Power System in Refinery Plant
YU Ming-xin, DONG Ke-lin, ZHANG Feng-di
(West Pacific Petrochemical Co., Ltd., Dalian, Liaoning Dalian 116600, China)
Steam power system (SPS) is an important part of refinery plant. A mixed-integer linear programming (MILP) model was established to solve the problem of design and operation of steam power system in refinery plant. The method can decrease the operational cost through improving the structure and change the operational scheme of the system. One motivation example was introduced to optimize the design and operation of system, by the comparison, it was obvious to find the effectiveness of the proposed MILP model.
refinery plant; steam power system; optimization; MILP
于明欣(1982-),男,工程师,主要从事石油炼制、系统平衡与优化管理。
TK219
A
1001-9677(2016)023-0131-04

