城市快速路竞争与协作换道行为特征分析

李鹏飞，石建军，刘小明,2

(1．北京工业大学 交通工程北京市重点实验室，北京 100124；2．交通运输部，北京 100736)



城市快速路竞争与协作换道行为特征分析

李鹏飞1，石建军1，刘小明1,2

(1．北京工业大学 交通工程北京市重点实验室，北京 100124；2．交通运输部，北京 100736)

本文研究道路资源有限条件下车辆竞争与协作换道行为特性。在前人研究的基础上，对竞争换道行为进行了描述，并与协作换道行为进行了比较。采用视频拍摄和车辆轨迹提取软件获取了车辆换道数据。着重探讨了车辆换道距离和时间、骑线行驶距离和时间的内在联系，并对换道行为中车辆的接受间隙、速度变化、横向位移进行了分析。以实测数据为基础，得出竞争/协作换道行为下车辆换道接受间隙的分布函数，提出重合区域最小值法，得到竞争与协作换道接受间隙的临界值，并以此建立了不同间隙下车辆换道行为的概率模型。研究结果表明：竞争/协作换道接受间隙的临界取值为19.28 m，车辆间隙大于30 m时车辆选择协作换道的概率为94.49%以上。

交通工程；换道；重合区域最小值法；竞争; 协作；城市快速路

0 引言

道路交通系统的平稳有序运行受到多方因素制约，不同的驾驶行为，特别是一些非常规驾驶行为对交通安全带来潜在威胁。根据德国NVENT-FAS协会公布的道路交通事故主要原因分析报告，在车辆行驶过程中并线、车道变换和驶离车道行为造成的事故占总事故数的28%和15%[1]。车辆竞争行驶过程中由于冲突点的增加影响交通运行效率，威胁交通运行安全，降低交通系统安全性，甚至可能引发道路交通阻塞等不良后果。因此，对通行行为，尤其是以竞争性换道为代表的通行行为进行研究[2]，对于完善通行行为分析研究方法、提高个体驾驶行为研究水平、更好地理解人-车-路协同关系具有重要意义。

现有研究将换道行为分为3个阶段：换道需求产生、换道可行性判断和换道过程执行。在换道需求产生方面，驾驶人换道需求由当前车道和目标车道的交通状况所决定，主要采用换道概率来描述车辆的换道需求。Yang等[3]建立的车辆换道需求由车辆期望速度和前车速度来决定，并通过忍耐因子和速度差因子等参数来确定当前车速是否足够低，相邻车道速度是否足够大，以此来判断车辆是否换道。郑弘等[4]将随机效用理论引入换道需求的产生，建立了基于效用选择的换车道模型。在换道决策方面，相关学者进行了大量的研究，取得了丰富的研究成果。针对Gipps框架[5]没有区分不同换道性质的缺点，Yang[6]根据驾驶人动机的不同，将换道分为强制性换道(Mandatory Lane Changing，MLC)和判断性换道(Discretionary Lane Changing，DLC)。Wei等[7]通过交通视频观测，在强制性换道和判断性换道的基础上，提出预先换道(Preemptive Lane Changing，PLC)，表明换道行为具有长期的行为动机，并且驾驶人的临界接受间隙在不同情况下是不同的。Hidas[8]发现在拥堵条件下驾驶人竞争换道行为(Forced Lane Change，FLC)，将换道决策类型分为自由换道、合作换道和竞争换道3种，使用智能Agent技术模拟驾驶人的反应和换道过程中的相互作用，根据道路拥堵水平和个体Agent的特性差异，智能体选择让出空间、减速、或者不退让。Toledo等[9]提出了综合驾驶行为模型，使用离散概率模型来描述驾驶人的车道选择和间隙选择，允许驾驶人同时考虑MLC和DLC两种换道类型。Balal等[10]利用Next Generation Simulation (NGSIM)中I-80高速公路的车辆轨迹数据，提出了基于模糊推理系统的驾驶人换道决策二元选择模型，结果显示该方法精度优于传统的接受间隙模型。Zheng等[11]采用神经网络模型来研究多样性的换道行为，并利用车辆轨迹数据对模型进行评估和验证，并与多项Logit模型进行了对比，研究显示，神经网络模型能够预测94.58%的左侧换道和73.33%的右侧换道，优于多项Logit模型的13.25%和3.33%的准确预测比例。Singh等[12]为研究换道行为对交通流的影响，提出了用马尔科夫链空间状态模型来描述驾驶人换道行为。Talebpour等[13]提出了一种基于博弈理论的换道模型，建立了双人非零和非合作博弈框架，并使用NGSIM轨迹数据进行验证，仿真结果表明此模型比间隙接受模型更符合实际情况。

国内学者对换道行为进行了较为深入的研究[14-15]。王崇伦等[16]建立了动态椭圆最小安全距离模型，较之传统最小安全距离模型的约束空间具有更高的安全性和灵活性，并采用回旋曲线解决了圆弧换道模型的侧向加速度过大、曲率不连续等问题。杨晓芳等[17]分析了驾驶过程中的博弈行为和相应驾驶行为意图的变化，建立了前后车之间的博弈矩阵模型。

目前的换道研究侧重于换道需求产生、间隙检测等决策过程的分析，然而对换道实施过程具体行为细节的研究更为重要。党睿娜等[18]在高速公路上进行了实车驾驶人换道试验，研究了换道阶段的车辆、车间状态变化和换道操作习惯等，其试验在自由流情况下进行，车辆密度较小，属于自由换道行为。Zhao[19]观察国内车辆换道行为，提出了多步式挤压换道行为，与标准换道、合作换道、强制换道在换道时间、车道分布、影响程度等方面进行了对比。综上所述，研究者在换道需求产生、行为表现、决策等领域进行了广泛的探索。在我国，交通拥堵常态化，多数驾驶人法规道德意识淡薄，驾驶人的换道大多属于见缝插针的竞争行为，现有研究缺乏对竞争与协作换道行为在特征指标上的分析，尚无竞争与协作换道行为特征指标临界值的分析方法。因此本文将对上述问题进行相关研究。

本文通过车辆运动视频提取车辆换道行为轨迹数据，在总结前人研究成果和交通专家讨论的基础上，归纳出竞争与协作目标车辆的外显运动特征，分析换道行为中车辆的行驶轨迹，比较换道距离和时间、车辆速度、接受间隙、车辆横向位移等外显运动参数，进而得到驾驶人竞争与协作换道行为的交通特征参数。针对目前尚无竞争与协作换道行为特征指标判别方法的不足，提出重合区域最小值分析法，用于获取不同换道行为特征指标的临界值，并计算两种换道类型的概率。

1 竞争驾驶行为表现

一般来说，车辆换道行为包括3个方面：(1)驾驶人决定实施换道行为，调整方向盘使车辆偏转，以一定的角度跨越车道线进入目标车道；(2)车辆进入目标车道后，反向调整车辆方向；(3)驾驶人对车辆方向进行微调，以使车辆能够在目标车道上安全行驶。

基于目标车辆和目标车道后车不同的交互行为，传统的驾驶人换道过程分为自由换道、合作换道和强制换道3种。换道过程中车辆的运动过程可分为转向、直线加/减速、并道。在西方国家，3种换道行为能够解释道路上大多数驾驶人的换道行为。在我国，受周围环境、社会文化以及自身道德水平等多方面因素影响，驾驶人多采用竞争式通行行为，与发达国家的协作式通行行为存在显著差异[20]。

为更好地分析换道行为，建立车辆换道行为的交通环境，如图1所示。①为目标车辆，②为目标车道前车，③为目标车道后车，④为本车道前车。AD段为目标车辆从换道开始到结束的全过程，BC段为目标车辆骑线行驶(Trans-line Ride，TLR)部分。协作换道行为，即①车发出换道请求，③车减速允许其换道请求，随后①车检查换道间隙完成换道。竞争换道行为比较复杂，Sun基于目标车道后车决策行为，提出了竞争/合作(Competitive/Cooperative，C/C)换道行为[21]，认为竞争换道为：①车发出换道请求，③车保持车速或加速拒绝其换道请求，然后①车继续向后车发出换道请求，直到目标车道后车减速允许其换道请求。Zhao提出的多步式挤压换道行为认为，①车在被拒绝其换道请求后会逐步靠近目标车道，降低车速，逼迫③车减速让行，直到出现可供目标车辆完成换道行为的换道间隙。

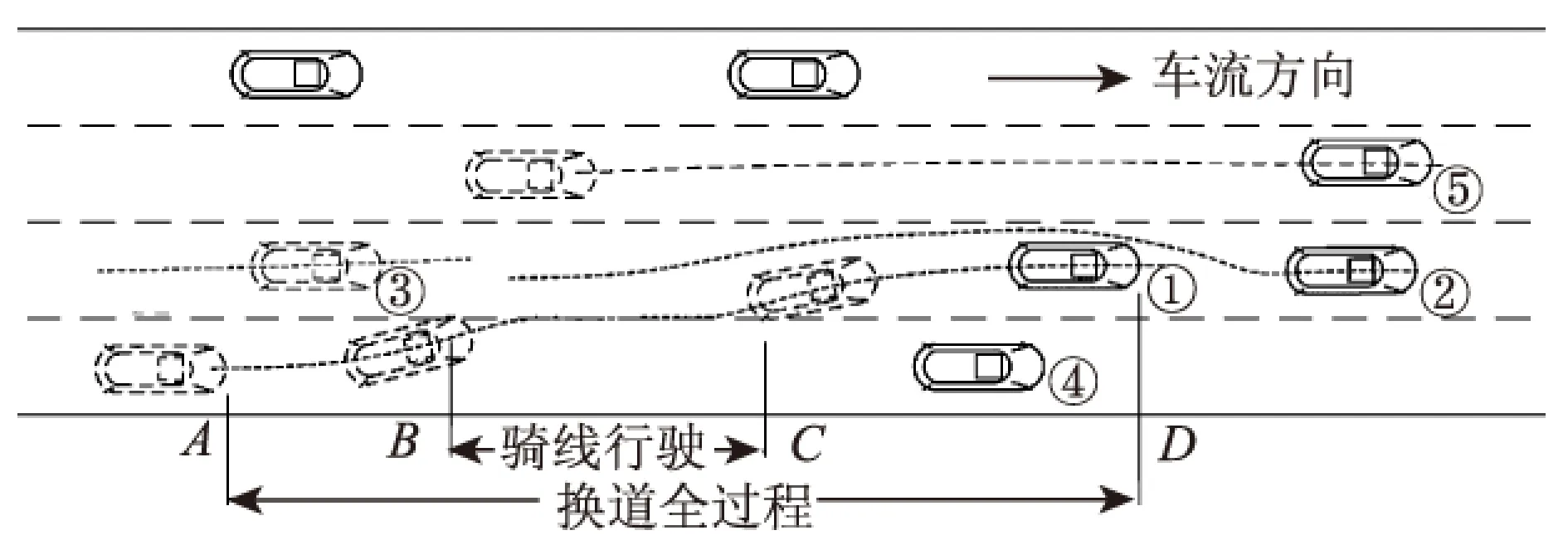
图1 车辆换道关系示意图Fig.1 Schematic diagram of lane-changing relations between vehicles

车辆换道行为的竞争与协作是一个相对的概念，任何换道行为的完成或放弃都是一方礼让或者妥协的产物，表现为双方驾驶人的博弈平衡，否则驾驶人之间的完全竞争将会导致交通事故的发生。因此，本文在定义竞争换道行为还是协作换道行为时，以双方第1次冲突时对方的行为反应为判定准则。

(1)协作换道行为

如图2(a)所示，①车向③车发出换道请求，③车允许其换道请求同时减速增大换道间隙，为①车换道提供条件。

(2)竞争换道行为

如图2(b)所示，①车在换道条件不充分的条件下(主要表现为换道间隙小于临界间隙)，向③车发出换道请求，③车选择拒绝其换道请求。此时③车可能存在两种反应：③车保持原有速度，维持现跟驰状态；③车加速，减小与前车间距。若①车坚持换道需求，则为竞争换道行为。

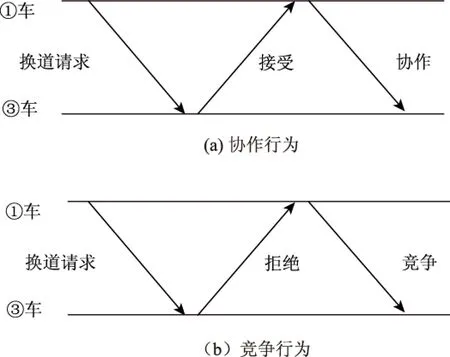
图2 车辆换道交互关系图Fig.2 Diagrams of lane-changing interactions between vehicles

根据前人对竞争与协作换道行为特性的研究，同时对15名驾驶人进行访谈，最后结合专家意见，从定性的角度建立驾驶人竞争与协作换道行为辨别方法与标准。

(1)车辆间距

在道路资源有限的交通环境中，目标车辆为了争夺道路优先权，换道行为需求的产生和执行在换道条件不充分的条件下进行，目标车道前后车间隙小于临界间隙，目标车辆通过“挤压”后车完成竞争换道。

(2)换道时间

竞争换道环境下，目标车辆与目标车道前后车存在交互行为，特别是目标车辆与后车之间存在激烈的博弈，呈现你争我抢的局面，导致目标车辆速度降低、换道时间增加。

(3)速度变化

当目标车辆发出换道请求，后车拒绝，目标车辆会逐渐靠近目标车道，同时降低车辆速度，通过不断向目标车道后车施加压力，最终完成换道。

(4)骑线行驶

竞争条件下，目标车辆不可能一次完成换道，为了向后车施加压力，表明其换道的坚决性，会沿车道边缘甚至骑线行驶(Trans-line Ride，TLR)，竞争换道中目标车辆沿车道边缘行驶时间和距离增加。

(5)目标车道车辆横向偏移

目标车辆逐渐靠近目标车道，挤压目标车道前车或后车，使得前车或后车被迫偏离车道中心，造成目标车道车辆的横向偏移。

图3(a)和(b)描述了两种典型的驾驶人竞争换道行为。图3(a)中，①车在不满足换道条件的情况下，选择向目标车道偏移，选择合适的机会强行汇入车队，并强迫目标车道②车做出让步，然而②车只是向车道边缘偏移而并未让步，而是选择与之竞争，两车在同一车道并行一段距离后，②车选择加速，超越目标①车，至此换道结束。而在图3(b)中，①车在向目标车道偏移的过程中，逐渐减小与②车之间的横向距离，迫使②车减速让行，完成换道。

图3 典型竞争换道行为Fig.3 Typical competitive lane-changing behaviors

2 数据采集与处理

2.1 数据采集方案

为了获得车辆竞争换道数据，选取北京快速路窑洼湖桥一段进行交通视频采集。为了提高调查数据的精度，采用高点视频拍摄、视频车辆轨迹提取的方法。车辆视频轨迹数据采集流程如图4所示。

图4 视频数据处理流程图Fig.4 Processing of video data processing

2.2 数据采集

通过对窑洼湖桥周边环境的筛选，选取快速路自南向北作为观测对象。摄像机架设在人行天桥，通过4 m长的拍摄杆固定在顶端，尽量提高拍摄高度扩大拍摄范围。通过经纬仪等测量仪器对道路主要标志点进行坐标测量。数据采集时间为2015-03-24至2015-03-25共6 h视频，竞争与协作样本见表1。利用视频处理软件Ulead Video Studio将视频处理为10 Hz的视频图像。然后使用SIMI Motion 3D系统通过视频加载、坐标基准点标定、坐标变换、车辆运动轨迹采集、运动数据导出得到车辆的坐标、速度、加速度和运动距离等数据。最后经过简单的数据处理即可得到车辆的速度、车头间距、换道时间、骑线行驶距离和时间等参数。

表1 视频采集及竞争与协作换道行为样本

2.3 参数处理

为研究车辆的竞争行为特征，首先需要确定车辆的换道行为定义，其次对所采集数据进行统计分析。如图1所示，目标车辆换道起终点为A点、D点，B点、C点分别为目标车辆骑线行驶的起终点。车辆换道行为参数主要包括换道时间和距离、骑线行驶距离和时间、目标车辆换道接受间隙、目标车辆速度、目标车道后车横向位移等参数。

3 换道行为参数特征分析

基于上文的竞争换道行为特性和换道相关参数定义，提取车辆竞争与协作换道行为轨迹。对车辆换道距离和时间、换道接受间隙、目标车辆减速值、骑线行驶距离和时间、后车横向位移等参数进行分析，见表2。

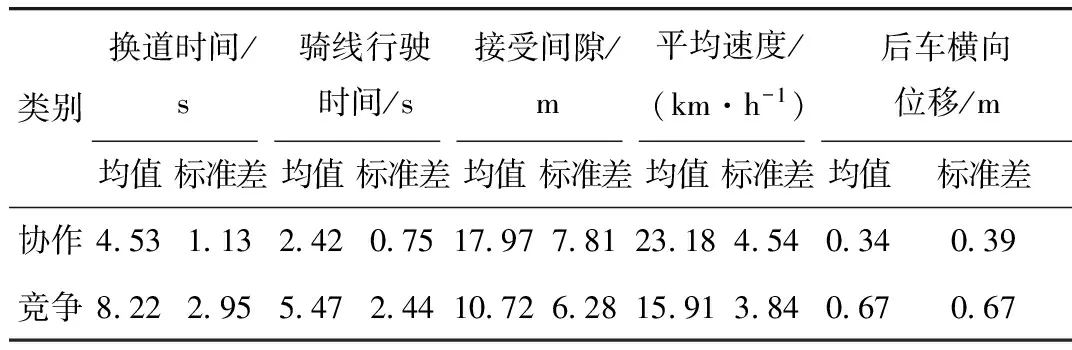
表2 竞争与协作换道行为特性参数描述性统计

3.1 换道距离和时间

车辆换道时骑线行驶距离和时间是换道行为中的重要参数，是车辆换道总距离和总时间的组成部分。

图5为两种换道行为中车辆换道时间与骑线行驶时间的关系图。车辆换道过程中，骑线行驶时间随着总换道时间的增加而增加。对换道时间和骑线行驶时间进行回归分析，协作与竞争行为系数分别为0.537和0.680，两者相差0.143。由此可见，协作换道的平均骑线行驶时间占总时间的比例明显小于竞争换道的骑线行驶时间所占的比例。这表明竞争换道不能一次性完成换道行为，目标车辆首先会逐步靠近车道线，并在车道线附近与目标车道车辆僵持，进行数次博弈后才能完成换道行为，使得压线行驶时间较长。

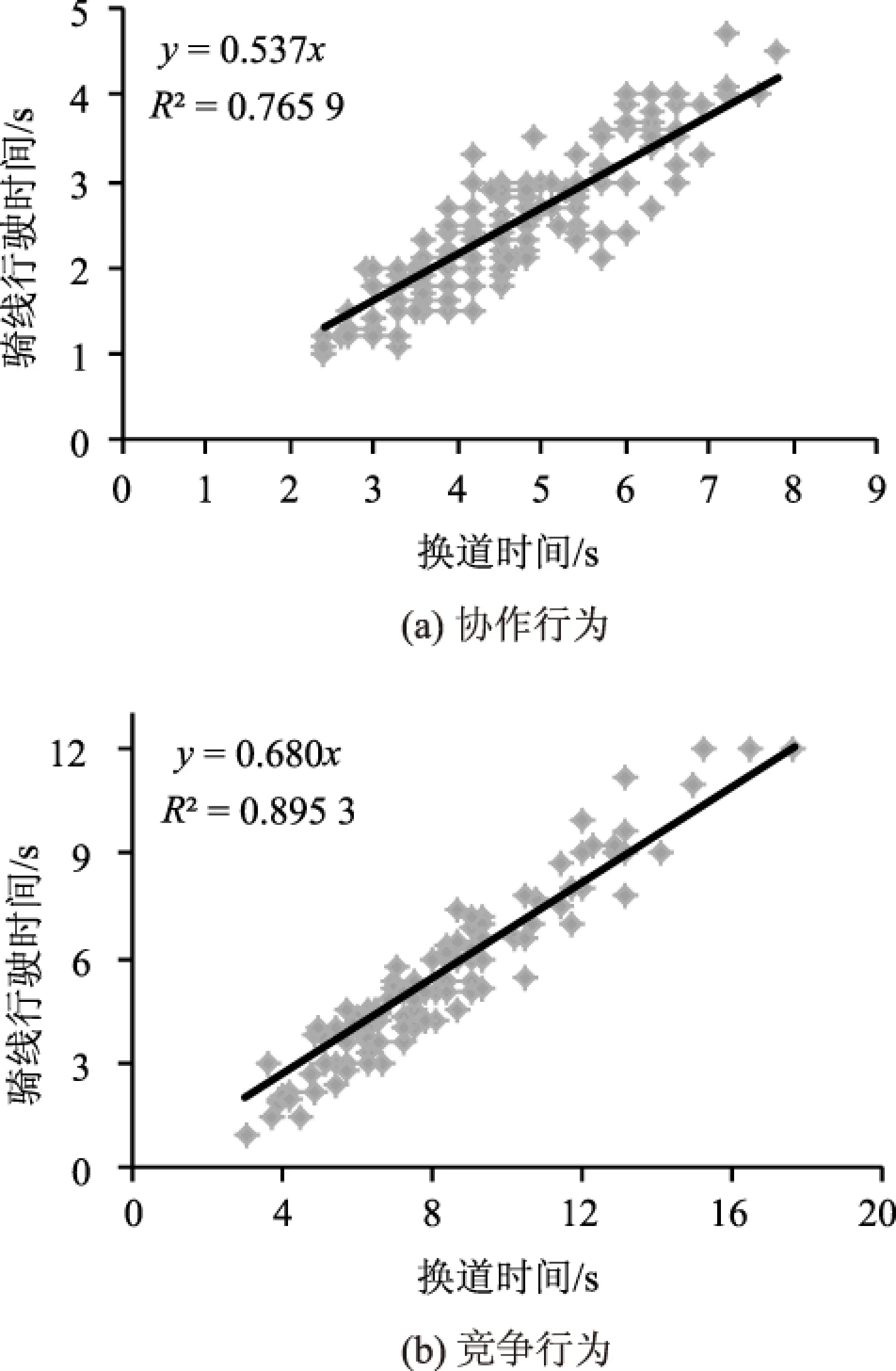
图5 换道时间与压线行驶时间关系Fig.5 Relations between lane-changing time and trans-line ride time

图6为车辆换道距离与骑线行驶距离的关系图。对换道距离和骑线行驶距离进行回归分析，协作与竞争行为系数分别为0.521和0.596，两者相差0.075。同时间比值结果一样，协作换道的平均骑线行驶距离占总距离的比例小于竞争换道的骑线行驶距离所占的比例。

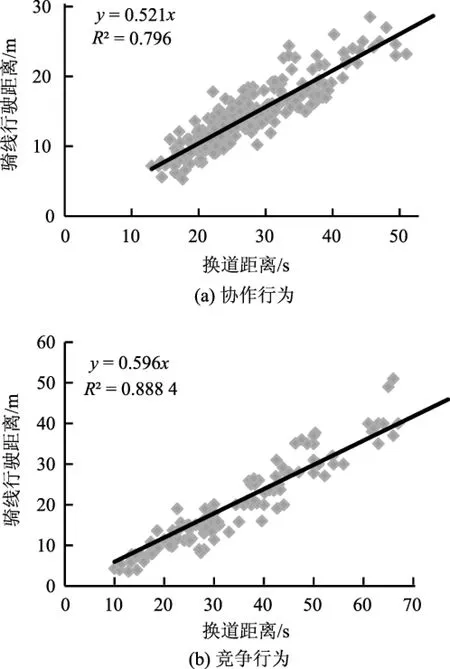
图6 换道距离与压线行驶距离关系图Fig.6 Relations between lane-changing distance and trans-line ride distance

比较车辆两种换道行为的距离、时间参数可以发现，协作换道的时间系数与距离系数只有0.016的差距，竞争换道的时间系数与距离系数差距则较为显著，达到了0.084。通过分析发现，产生这种现象的原因为：协作换道行为目标车辆的速度不会发生剧烈变化，车辆在换道过程中的加减速行为温和，车辆在骑线行驶过程中速度变化较小，所以两系数的值较接近；竞争换道行为中车辆之间存在激烈争抢行为，目标车辆在创造/等待接受间隙的过程中会逐步接近车道线，同时降低车辆速度，速度的降低使得车辆能够在更安全的环境下进行道路资源的争夺，造成目标车辆在车道线附近速度降低较大，因此，两系数的值差距也就较大。

换道过程中目标车辆换道平均速度与骑线行驶平均速度的相对比值为：

(1)

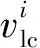
对实测数据进行分析，得到各目标车辆的换道平均速度与骑线行驶平均速度，计算得到竞争与协作换道行为中目标车辆的速度相对比值分别为-18.7% 和-2.1%。反映出两种换道行为特性的差异。

图7为车辆竞争/协作换道时间分布和累积频率统计。协作换道时间集中在3～5 s之间，均值为4.2 s；竞争换道时间分布范围较大，均值为8.2 s，图7(b)中出现两个峰值，分别为6～8 s和12～14 s，明显高于协作换道时间。

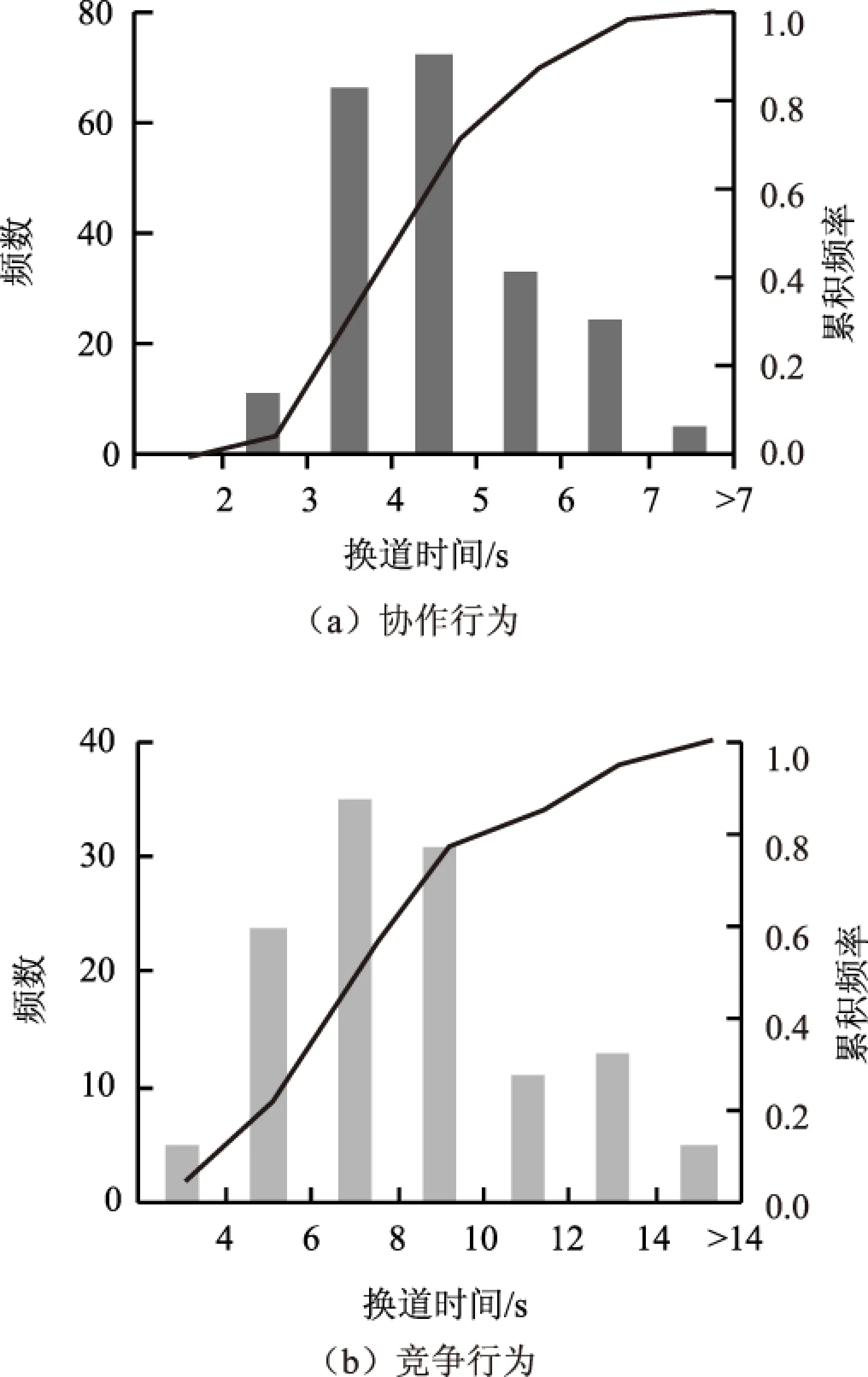
图7 换道时间分布和累积频率Fig.7 Lane-changing time distribution and cumulative frequency

3.2 换道接受间隙

不同换道行为对换道可接受间隙的选择也不相同，如图8所示。竞争换道的接受间隙均值为10.7 m，其中间隙为0～15 m占总数的81%；协作换道的接受间隙均值为18 m，其中间隙为10～30 m，占总数的82%。

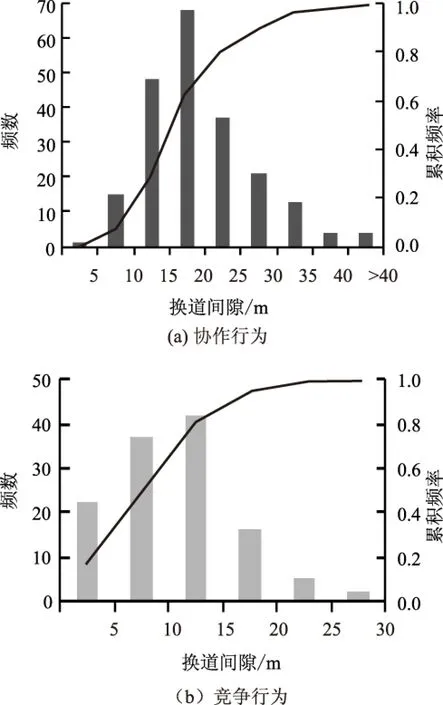
图8 换道接受间隙分布和累计频率Fig.8 Lane-changing acceptance gap distribution and cumulative frequency

竞争换道行为的接受间隙在0～5 m中的占总数的18%，5 m的间隙根本不能满足车辆的换道需求，结合骑线行驶时间，充分说明了目标车辆在换道需求强烈且换道条件不满足的条件下，与周围车辆争夺道路资源的激烈程度。

3.3 目标车辆速度

不同换道行为中，目标车辆的速度变化也不相同。对目标车辆在换道初始时刻A点和骑线行驶末端时刻C点速度进行统计，如图9所示。直线表示车辆在换道初始时刻和压线行驶末端时刻的速度相等，直线下方表示车辆换道初刻速度大于骑线末端速度，直线上方表示车辆换道初刻速度小于骑线末端速度。可以看出，协作换道中的大部分目标车辆在完成换道任务时速度会增加，占总数的82.9%；竞争换道中的大部分目标车辆在完成换道任务时速度会减小，占总数的73.4%。竞争目标车辆速度的减小会对交通流的平稳运行造成干扰，尤其在道路交通量接近饱和的状态下，交通流的轻微扰动就可能导致交通阻塞。

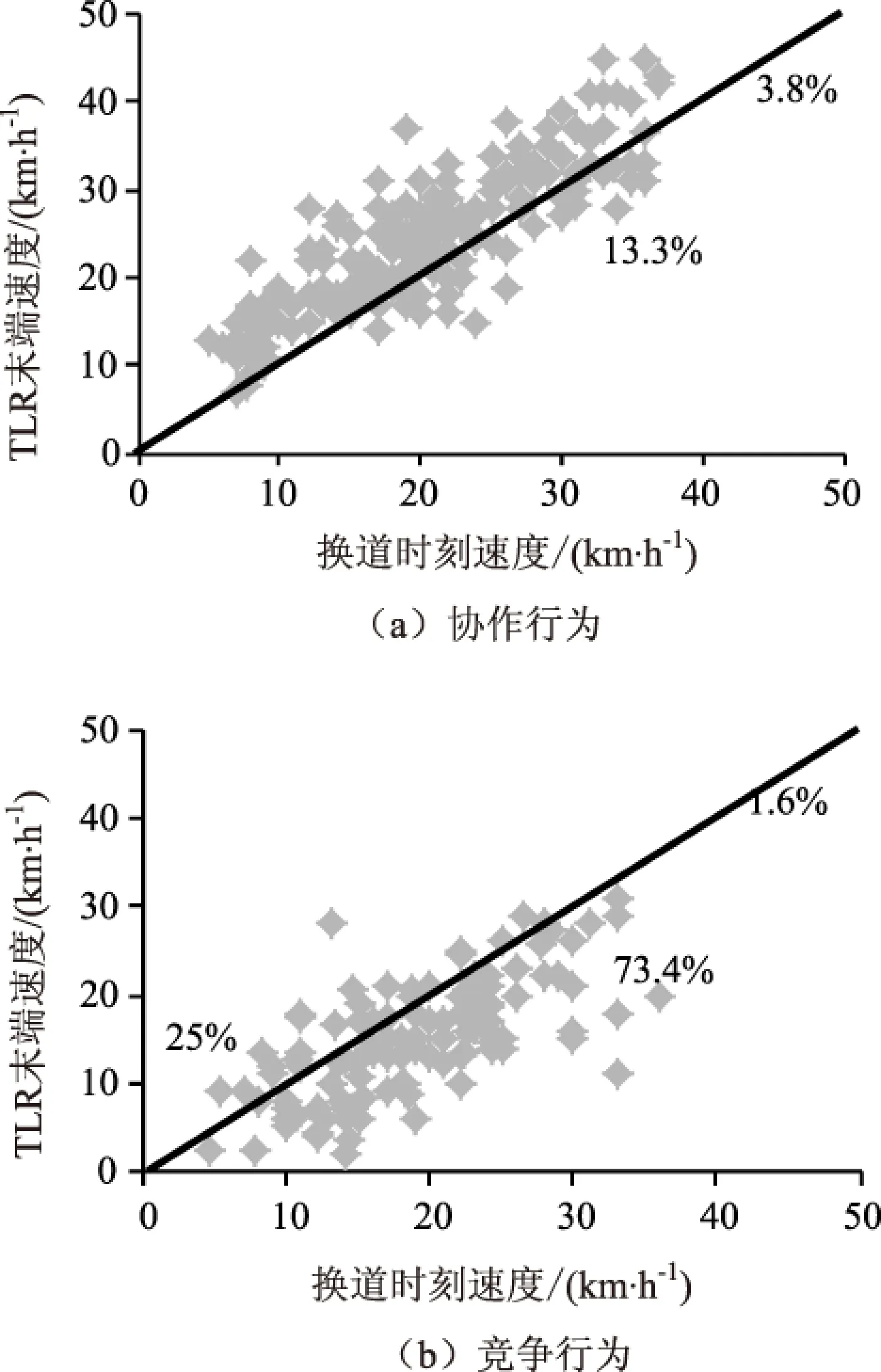
图9 车辆换道初刻和压线末端速度散点图Fig.9 Scattergram of velocities at lane-changing initial time and TLR end time

3.4 后车横向位移

目标车道后车横向位移，即在换道过程持续时间T内，目标车道后车相对换道初始时刻的横向最大位移为：

(2)

表3为目标车道后车横向位移统计。协作换道中有81%的后车横向位移在0～0.5 m范围内，竞争换道则仅占总数的54%，近一半的后车位移在0.5 m以上，其中21.8%的后车横向位移大于1 m。统计结果表明，在竞争换道过程中，目标车辆往往无足够的换道间隙，在逐步向目标车道行驶的过程中“挤压”后车“创造”换道间隙，此行为会对后车造成较大的横向压力，后车为保证行车安全向车道边缘移动，使得车辆横向位移偏大。如果后车的临近车道存在适合换道的车辆间隙，后车甚至会采取换道行为来消除横向压力。

表3 目标车道后车横向位移

4 换道行为概率分析

不同的换道行为表现出不同的换道行为特性，构建车辆换道行为模型需要对车辆换道类型进行预测。上文分析了换道过程中车辆换道距离、时间、接受间隙、速度、横向位移等参数，在这些参数中，车辆换道距离、时间、速度、横向位移参数为换道过程完成后才能获得的参数，接受间隙为换道开始前就能获得的参数。因此，选取接受间隙作为换道类型的预测变量。

2.1 换道接受间隙分布函数

观察两种换道类型的换道接受间隙分布，总体上类似于韦伯分布或正态分布。利用实测接受间隙数据对两种分布进行拟合，得到竞争与协作换道下换道接受间隙的拟合参数值，如表4所示。

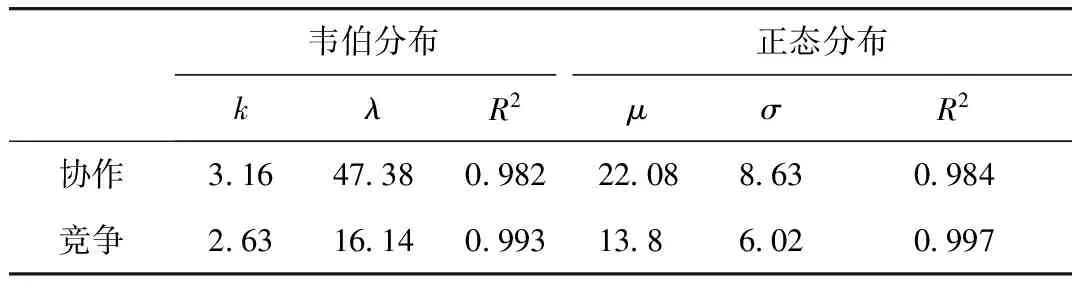
表4 换道接受间隙分布函数的拟合参数

注：k为形状参数；λ为比例参数；R2为判定系数;μ为期望值，决定其位置；σ为标准差，决定分布幅度。

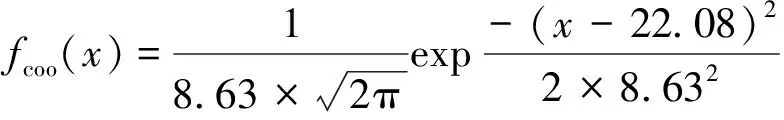
4.2 竞争与协作换道行为概率

为了更准确地表征驾驶人竞争与协作驾驶的行为特性，合理划分驾驶人竞争与协作换道概率，采用重合区域最小值法确定竞争与协作换道接受间隙的临界值。

如图10所示，假设接受间隙临界值为a，为使大于临界值a被误判为竞争换道和小于临界值a被误判为协作换道的概率最小，即求得图10中阴影面积之和最小，则公式为：

(3)

式中，Fcoo(x)为fcoo(x)对应的密度函数；Fcom(x)为fcom(x)对应的密度函数。

将式(3)展开，得到：

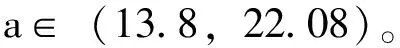
(4)

将竞争与协作的密度函数代入式(4)中，计算得到x=19.28 m，取得最小值0.558，即竞争与协作换道接受间隙的临界值为19.28 m。

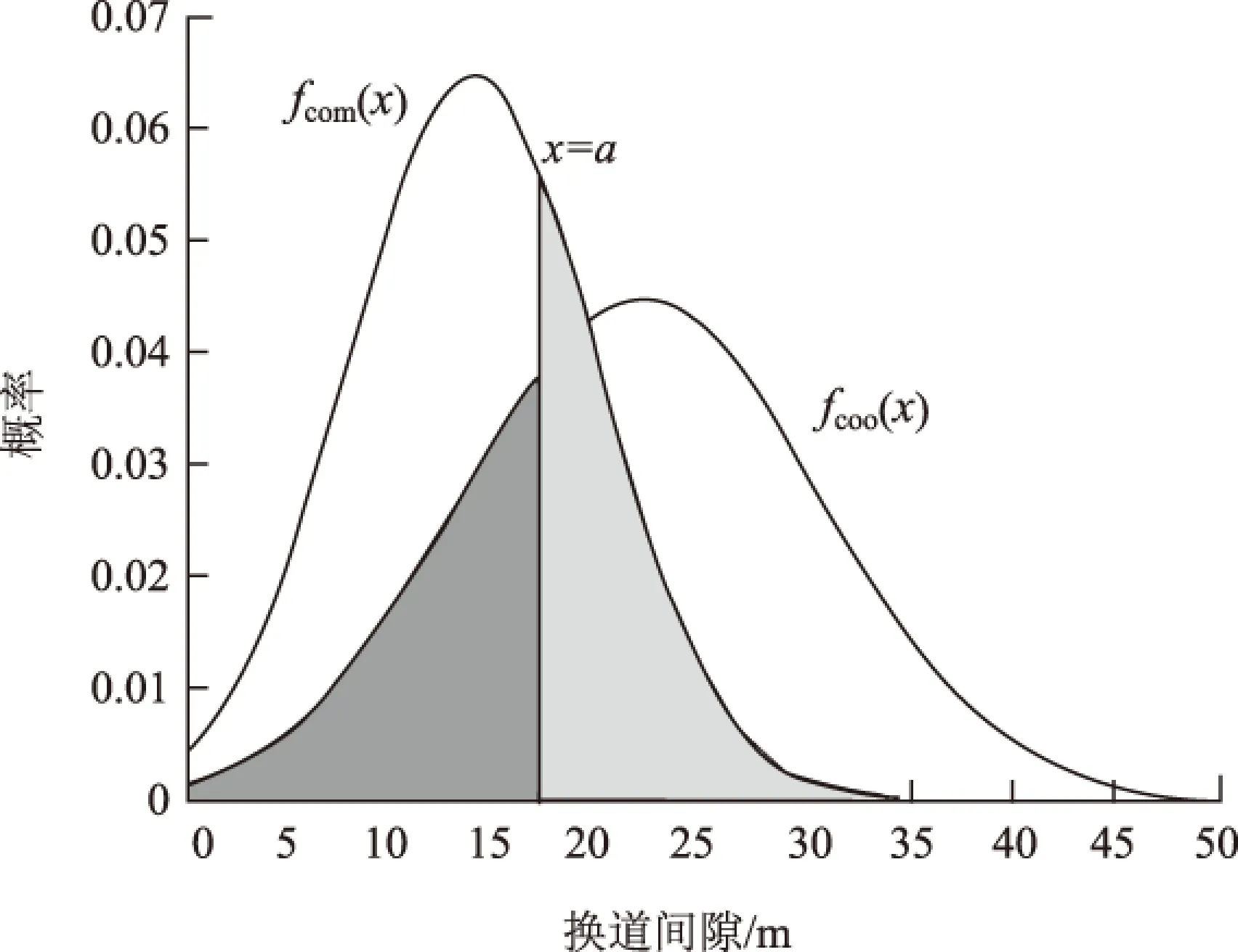
图10 竞争与协作换道接受间隙分布Fig.10 Acceptance gap distribution of C/C lane changing

结合竞争与协作换道行为的换道接受间隙分布函数，采用概率形式来表示驾驶人的竞争与协作换道选择行为：

(5)

(6)

式中，pcom(x)为换道间隙为x时目标车辆选择竞争换道的概率；pcoo(x)为换道间隙为x时目标车辆选择协作换道的概率。

基于以上建立的换道行为选择概率模型计算得到不同间隙下车辆的竞争与协作换道行为的概率，见表5。

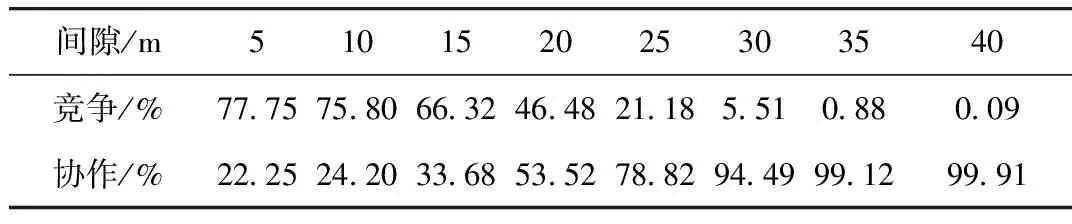
表5 不同间隙车辆换道行为选择概率

当间隙小于15 m时，目标车辆换道采取竞争行为的概率较大；当间隙大于20 m时，目标车辆采取竞争行为换道的概率下降明显，而采取协作换道的概率增大；当间隙等于30 m时，车辆选择协作换道的概率为94.49%，表明30 m以上的车辆间距已经足够使车辆从容地完成换道。

5 结论

(1)竞争行为的换道时间为8.22 s，远高于协作行为换道时间4.53 s；竞争换道行为中换道接受间隙为0～15 m，占总数的81%，协作行为占总数的30%；竞争换道中目标车辆的平均速度比协作换道的平均速度低7.27 km/h；竞争行为中目标车道后车横向位移为0.67 m，是协作行为的2倍。表明竞争换道行为换道时间长、速度降低大、对周围车辆影响严重。

(2)根据实测数据，对两种换道类型的目标车辆换道接受间隙进行了分布拟合，结果表明竞争与协作换道行为的换道接受间隙能够很好地拟合正态分布，并给出了密度函数。

(3)基于接受间隙分布函数，提出了重合区域最小值法，以确定竞争与协作换道接受间隙的临界值。间隙取值为19.28 m时可使两类换道行为的误判概率最小，并给出了不同车辆间距下竞争与协作换道行为的概率。

(4)驾驶人换道接受间隙及换道行为方式的选择受多种因素的影响。本文仅考虑城市快速路交通流量大的情况下车辆接受间隙对换道行为的影响，没有对个人属性、交通流量、速度、车辆性能等因素进行分析。因此，有必要在后续研究中将这些因素在换道选择概率模型中加以体现，以获取更加准确的预测结果。

[1] 陈俊. 基于DSP的汽车视觉系统研究[D]. 武汉: 武汉理工大学, 2009. CHEN Jun. Research of Automotive Vision System Based on DSP[D]. Wuhan: Wuhan University of Technology, 2009.

[2] 石建军,李鹏飞,刘小明,等. 道路通行行为研究进展及其展望[J]. 交通信息与安全, 2015, 33(2): 1-9. SHI Jian-jun, LI Peng-fei, LIU Xiao-ming, et al. Progress and Prospect of Research on Road Traffic Behavior [J]. Journal of Transport Information and Safety, 2015, 33(2): 1-9.

[3] YANG Q I, KOUTSOPOULOS H N. A Microscopic Traffic Simulator for Evaluation of Dynamic Traffic Management Systems[J]. Transportation Research Part C: Emerging Technologies, 1996, 4(3):113-129.

[4] 郑弘, 荣建, 任福田. 基于效用选择的换车道模型[J]. 公路交通科技, 2004, 21(5): 88-91. ZHENG Hong, RONG Jian, REN Fu-tian. A Lane Changing Model Based on Random Utility Theory[J]. Journal of Highway and Transportation Research and Development, 2004, 21(5): 88-91.

[5] GIPPS P G. A Model for the Structure of Lane-changing Decisions[J]. Transportation Research Part B: Methodological, 1986, 20(5):403-414.

[6] YANG Q. A Simulation Laboratory for Evaluation of Dynamic Traffic Management Systems [D]. Cambridge: Massachusetts Institute of Technology, 1997.

[7] WEI H, LEE J, LI Q, et al. Observation-based Lane-vehicle Assignment Hierarchy: Microscopic Simulation on Urban Street Network[J]. Transportation Research Record, 2000, 1710(1):96-103..

[8] HIDAS P. Modelling Vehicle Interactions in Microscopic Simulation of Merging and Weaving[J]. Transportation Research Part C: Emerging Technologies, 2005, 13(1):37-62.

[9] TOLEDO T, KOUTSOPOULOS H N, BEN-AKIVA M. Integrated Driving Behavior Modeling[J]. Transportation Research Part C: Emerging Technologies, 2007, 15(2):96-112.[10]BALAL E, CHEU R L, SARKODIE-GYAN T. A Binary Decision Model for Discretionary Lane Changing Move Based on Fuzzy Inference System[J]. Transportation Research Part C: Emerging Technologies, 2016, 67:47-61.[11]ZHENG J, SUZUKI K, FUJITA M. Predicting Driver’s Lane-changing Decisions Using a Neural Network Model[J]. Simulation Modelling Practice & Theory, 2014, 42:73-83.[12]SINGH K, LI B. Estimation of Traffic Densities for Multilane Roadways Using a Markov Model Approach[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4369-4376.

[13]TALEBPOUR A, MAHMASSANI H S, HAMDAR S H. Modeling Lane-changing Behavior in a Connected Environment: A Game Theory Approach[J]. Transportation Research Part C: Emerging Technologies, 2015, 59: 216-232.

[14]刘志强, 王俊彦, 汪澎, 等. 基于BP神经网络的高速公路入口合流区域换道行为研究[J]. 公路交通科技, 2014, 31 (9): 120-153. LIU Zhi-qaing, WANG Jun-yan, WANG Peng, et al. Study on Lane Change Behavior on Expressway On-ramp Merging Area Based on BP Neural Network[J]. Journal of Highway and Transportation Research and Development, 2014, 31 (9): 120-153.

[15]杨晓芳, 周昱, 付强. 考虑驾驶心理的封闭式道路车辆出匝换道模型[J]. 公路交通科技, 2015, 32(7): 112-119. YANG Xiao-fang, ZHOU Yu, FU Qiang. A Lane-changing and Off-ramp Model of Vehicles on Enclosed Road Considering Driving Psychology[J]. Journal of Highway and Transportation Research and Development, 2015, 32(7): 112-119.

[16]王崇伦，李振龙，陈阳舟，等. 考虑换道约束空间的车辆换道模型研究[J]. 公路交通科技, 2012, 29(1):121-127. WANG Chong-lun, LI Zhen-long, CHEN Yang-zhou, et al. Research on Lane-changing Models Considering Restricted Space[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1):121-127.

[17]杨晓芳, 张盛, 付强. 基于博弈论的完全信息下的驾驶行为研究[J]. 公路交通科技, 2015, 32 (7): 105-111. YANG Xiao-fang, ZHANG Sheng, FU Qiang. Research of Driving Behavior under Condition of Complete Information Based on Game Theory[J]. Journal of Highway and Transportation Research and Development, 2015, 32 (7): 105-111.

[18]党睿娜, 王建强, 李克强, 等. 高速公路行驶条件下的驾驶员换道特性[J]. 清华大学学报：自然科学版, 2013, 53(10): 1481-1485. DANG Rui-na, WANG Jian-qiang, LI Ke-qiang, et al. Driver Lane Changing Characteristics for Various Highway Driving Conditions[J]. Journal of Tsinghua University: Science and Technology Edition, 2013, 53(10): 1481-1485.

[19]ZHAO Li, SUN Jian, ZHANG H M. Observations and Analysis of Multistep Approaching Lane Changing Behavior at Two Expressway Merge Bottlenecks in Shanghai[C]// Transportation Research Board 92nd Annual Meeting. Washington,D.C.: Transportation Research Board, 2013.

[20]韦华, 张伟. 中美两国汽车驾驶安全影响因素研究[J]. 中国安全科学学报, 2004, 14(9): 24-28. WEI hua, ZHANG wei. Study on Factors Determining Driving Safety in China and the US [J]. China Safety Science Journal, 2004, 14(9): 24-28.

[21]SUN Jian. A Lane-changing Model for Urban Arterial Streets[D]. Gainesville, FL: University of Florida, 2009.

Analysis on Cooperative/Competitive Lane-changing Behavior Characteristics on Urban Expressway

LI Peng-fei1，SHI Jian-jun1，LIU Xiao-ming1,2

(1. Beijing Key Laboratory of Traffic Engineering, Beijing University of Technology, Beijing 100124, China;2. Ministry of Transport, Beijing 100736, China)

The present study aims to investigate the cooperative/competitive lane-changing behavior characteristics in the limited road resources. Based on the predecessors’ researches, the competitive lane-changing behavior is described, and compared with the cooperative lane-changing behavior. The lane-changing data are obtained by video capture and vehicle trajectory extraction. The internal relations among lane-changing space and time, trans-line ride (TLR) space and time are discussed, and acceptance gap, velocity change of object vehicle, horizontal displacement of lag vehicle are analyzed. Based on the measured data, the distribution functions about the acceptance gap of cooperative/competitive lane-changing are obtained. The critical value of the acceptance gap of cooperative/competitive lane-changing is extracted through the proposed method of minimum overlap area value, and the lane-changing behavior probability model for different acceptance gaps is established accordingly. The research result indicates the critical value of the acceptance gap of cooperative/competitive lane-changing is 19.28 m, the probability of cooperative lane-changing is more than 94.49% when the gap is more than 30 m.

traffic engineering; lane-changing; method of minimum overlap area value; competition; cooperation; urban expressway

2015-12-03

北京市教育委员会重点项目(KZ20151005007)

李鹏飞(1989-)，男，河南济源人，博士研究生.(689pengfei@sina.com)

10.3969/j.issn.1002-0268.2016.12.021

U491.1

A

1002-0268(2016)12-0130-10