基于Hoek-Brown强度准则的近接交叉隧道围岩参数计算方法

谢宝琎,张向东

(1. 辽宁工程技术大学 土木与交通学院，辽宁 阜新 123000;2. 中铁七局集团第三工程有限公司，陕西 西安 710000)



基于Hoek-Brown强度准则的近接交叉隧道围岩参数计算方法

谢宝琎1, 2,张向东1

(1. 辽宁工程技术大学 土木与交通学院，辽宁 阜新 123000;2. 中铁七局集团第三工程有限公司，陕西 西安 710000)

为利用在工程领域中使用广泛的Hoek-Brown强度准则，须对此进行修正，使其适用于各向异性岩石力学参数的计算。本文综合考虑了交叉隧道净距对围岩强度的影响，将Hoek-Brown准则中的扰动系数与净距关系进行量化并经过理论推导和数值模拟验算，得到了在上下隧道不同净距影响下的修正后Hoek-Brown公式。利用修正后的强度公式计算出结果与实测数据对照，结果相吻合。表明了修正后的Hoek-Brown强度公式能更好的反映出交叉隧道围岩的真实变形情况。

桥隧工程；近交叉隧道；修正Hoek-Brown强度公式；理论推导；修正

0 引言

隧道围岩的力学参数对工程设计及其稳定性研究有着举足轻重的作用。从20世纪40年代开始，国内外先后进行了大量的岩体原位试验，通过围岩现场试验能够获得比较接近实际的岩体力学参数。对于隧道工程，若利用现原位测试方法来获取围岩力学参数，时间较长且费用较高[1]。经验公式法求解隧道围岩力学参数涉及参数较多、应力场复杂，单纯依赖经典力学理论公式无法给出适合交叉隧道围岩的理论解。为寻求能适合交叉隧道围岩力学参数的方法，许多专家学者对隧道变形、应力、应变进行了大量研究。研究表明，以室内岩石试验为基础，综合考虑岩体完整程度、相邻隧道位置关系和尺寸效应的影响，对岩体力学公式进行修正后可以求出岩体力学参数以指导隧道的设计与施工。这些计算岩体力学参数的理论公式中经常被应用的主要有完整性系数(Kv)修正法、费森科(Г.Л. ФИCEHKO)方法[2]、格吉(M. Gergi)方法[3]以及霍克-布朗(Hoek-Brown)提出的围岩评级方法[4]，其中发展较为成熟应用较广的是Hoek-Brown强度准则，但由于Hoek-Brown强度准则在扰动系数选取上只能计算出极完整或极破碎情况下的扰动系数，所以它只能计算扰动和未扰动两种情况下的岩体力学计算公式。也就是说，对于天然形成未受扰动的岩体或是由于岩体自身崩解风化作用而形成极破碎岩体，这两种情况下岩体是各项同性的，可利用Hoek-Brown准则进行围岩强度计算公式；而对于大坝基础部位岩体、边坡岩石、隧道围岩这种介于扰动和未扰动之间的特殊岩体，岩体力学特征变为各向异性， Hoek-Brown 未能给出计算公式。张建海[5]等人对Hoek-Brown 公式的改进，其本质只是对扰动和未扰动情况下的系数求平均数，虽然使计算值与真实值误差减小，但并不等于真实情况下的岩体实际受扰动系数。闫长斌，徐国元[6]在张建海等人研究基础上对Hoek-Brown 公式进行进一步改进，他们尝试引入岩体完整性系数Kv，建立考虑岩体受扰动程度的修正系数Km和Ks，以便更好地确定介于扰动和未扰动之间的岩体力学参数。综上所述，若能引入若干参变量，对Hoek-Brown 公式中的扰动系数重新取值，便能够准确地计算出在交叉隧道情况下的围岩力学参数。

虽然国内外对岩石体力学计算公式进行了不断的修改，使其取得了广泛的工程应用，但是对交叉隧道围岩力学计算研究却很少。为了研究近接隧道交叉段围岩的变形规律，有必要对其进行深入研究。在隧道交叉段，围岩受到多次扰动，应力状态不断发生改变，随着两隧道净距增大两隧道间的相互扰动减小。本文依据前人对 Hoek-Brown 公式的改进，考虑了交叉隧道净距对围岩力学参数的影响，将隧道净距与扰动系数之间的关系进行量化，对 Hoek-Brown 公式进行了进一步的修改得到了岩体在隧道交叉体系中的应力应变规律。本文以草莓沟1#线上跨盘道岭隧道交叉段岩体力学参数研究为例，对本文改进公式和另外几种算法的计算结果与真实值进行了比较。计算结果表明，用本文公式确定的隧道交叉段的岩体力学参数与实际情况更为接近。

1 Hoek-Brown强度准则

Hoek和Brown基于Griffith的脆性断裂理论，通过室内岩石三轴试验及现场试验成果的统计分析，提出了Hoek-Brown屈服准则，该强度准则能够很好地反映岩体强度并且实用性很强，因此被国内外岩土工程界广泛采用，并且许多目前常用的数值分析软件如Flac、Phase2等都可以与Hoek-Brown准则结合对岩体的强度特性进行模拟，从而使模拟结果更接近实际[7]。Hoek-Brown准则经过不断的改进与修正，2002年版将爆破损伤和应力释放对围岩强度的影响引入到岩体扰动系数D中，并对Hoek-Brown常数mb,s和a进行修正，其表达式为：

(1)

式中，σ1，σ3分别为岩体破坏时的最大、最小主应力；σci为岩体的单轴抗压强度；mb，s，a均为岩体的Hoek-Brown常数；mb为Hoek-Brown常数mi(反映岩体软硬程度)的折算值；s反映岩体破坏程度，其取值范围在0～1之间； 各参数可由式(2)表示：

(2)

式中，mi为完整岩石的Hoek-Brown常数，可由室内试验得出，也可通过类比法确定；GSI值为地质强度指标，表征岩体破碎程度以及岩块镶嵌结构；D为表征岩体受扰动程度的参数。

2 近接隧道Hoek-Brown准则的修正方法

2.1 隧道交叉关系对岩体扰动的影响

一般来说单独洞室周围存在着具有规则几何形状的塑性区，对于新建和既有隧道交叉近接的情况，新建隧道开挖后造成了既有隧道相邻空间存在空洞，这个空洞改变了原有的塑性区和原始应力状态形成新的塑性区和应力状态。既有隧道与新建隧道上下最小净间距不同，隧道所在地层围岩应力场应力场状态也就不同。在既有隧道上方或下方地层中开挖近接隧道时，既有隧道围岩体产生应力释放，导致围岩初始应力场改变，随着净距增大，应力释放逐渐减小。在两个或多个近接隧道的情况下，若各个隧洞开挖的影响范围彼此互不重叠，则各洞室的开挖可视为与相邻洞室独立的单个洞室，彼此互不干扰，进行力学分析时可仅当做单个洞室开挖的情形予以考虑。而对于隧洞间间隔小于极限值的小净距隧道，各隧道间的影响范围存在叠加区域，新旧隧道存在相互干扰现象，使得隧道周围围岩的力学行为较独立隧道复杂。由于隧道近接距离的存在，围岩各力学测试指标数值较原先发生较大变化，这种变化与隧洞间隔密切相关。

2.2 交叉隧道扰动系数的选取

由Hoek-Brown强度公式可以看出mb，s，a等岩体参数选取对结果影响巨大。Hoek[7]等在2002版的Hoek-Brown强度准则中正式提出了扰动参数D的概念，但并没有对如何确定扰动系数给出具体的方法，在工程设计中如何界定岩体是否扰动也未给出具体的参照。以往对D值的选取一般都是按照不扰动时取0，部分扰动取0.5，完全扰动取1的取值方法，由此可见，Hoek建议的扰动参数D的取值原则比较模糊，可操作性不强。由于Hoek-Brown准则没有考虑到介于扰动和未扰动之间的情况，并且前人对Hoek-Brown准则的修改未能找到符合岩体实际扰动情况的参数，为克服 Hoek-Brown 准则及上述改进公式的不足，闫长斌，徐国元[6]在充分考虑了岩体受扰动程度后确定了的岩体完整性系数Kv的实际值，根据Kv与扰动系数的数值关系推导得出了修正系数Km，Ks，对Hoek-Brown 准则进行了修正，提出修正公式，即

(3)

(4)

这个改进后的公式较真实地反映了岩体受扰动程度的影响，因此具有很大的工程参考价值。

虽然前人对Hoek-Brown理论经过了多次修正，使得此公式更加科学，但是在围岩力学计算中，还没有针对于交叉隧道围岩力学参数计算的理论公式。隧道交叉情况下，围岩完整性受到净距的影响，宏观上看，若隧道净距较小则围岩扰动大，岩石完整性下降；同时随着净距减小，围岩可能从各向同性变为各向异性，从理论公式上应该存在围岩强度随着岩体完整性和净距减小而降低的数值关系，因此隧道近接交叉距离对岩体扰动系数D的选取有较大影响，只有引入净距这一参数才能得到接近实际情况的围岩强度。

为了得到考虑隧道净距扰动情况下的实际扰动系数，本人在闫长斌，徐国元[7]提出的Hoek-Brown修正公式基础上引入了隧道净距，对Hoek-Brown准则进行进一步改进，建立了一种既能考虑岩体受扰动程度的影响，同时又能考虑到上下交叉隧道相互空间位置关系影响下的围岩强度修正公式，即

(5)

(6)

式中，H为上下交叉隧道净间距(H<30 m)；Kv是岩石完整性系数；mi为完整岩石的Hoek-Brown常数。

由于岩石破碎程度、隧道净距H共同决定了岩体强度大小，所以本文经过大量验算[8]，对岩石完整性系数Kv、隧道净距H前的系数进行重新取值，以这两个重要参变量共同来表征交叉隧道岩体受扰动程度，在未进行速度测定的情况下，岩石完整性系数mi可按沈荣明，陈建峰合编岩体力学[9]书中表5-19 中所给的Kv值，根据现场岩体节理情况对Kv进行判读时，由于爆破产生大量非自然裂隙会让工程人员对Jv的判读产生误差，所以要对交叉段围岩整个围岩状况进行调查记录，参数的计算不能以开挖出露的围岩情况决定，而应该通过地质勘察得到的围岩情况来定性确定Kv。由于修正公式的构建过程中主要考虑的是近距离交叉的情况，参数的选取基于现场测量计算，在工程实践中根据日本铁道综合技术研究所发布的“隧道近接交叉施工指南”提出的隧道近接交叉施工影响范围分类以及交叉隧道相互影响范围的划分，H>2.5B时两隧道则无相互影响，此公式仅在近距离交叉即H>2.5B的情况下适用，对于非近接隧道，此公式并不适用。

在求得mb，ms后，即可利用 Hoek-Brown[10]提供的公式得出此种情况下的岩体力学参数：

(1)岩体抗压强度

在方程(1)中，令σ3=0 可得岩体的单向抗压强度，其方程为

(7)

式中，RmG为修正后岩体单轴抗压强度;σci为岩体的单轴抗压强度。

(2)岩体抗拉强度

Hoek[11]研究表明，对于破碎岩体，其单轴抗拉强度等于双轴抗拉强度。令σ1=σ3=σt可得出岩体的抗拉强度：

(8)

式中Rmt为修正后岩体单轴抗拉强度。

(3)岩体弹性模量

① Hoek等对我国大量岩土工程的岩体弹性模量数据进行回归分析，提出了计算岩石弹性模量的经验公式，其表达式如下：

(9)

② 徐国元提出的计算岩石弹性模量的经验公式，其表达式如下：

(10)

③ 本文在徐国元研究基础上提出了计算岩石弹性模量的经验公式，其表达式如下：

(11)

(4)围岩变形

在求得岩石弹性模量之后，便可根据相关公式求得围岩应变值，其值是否超过限值可作为评判围岩是否失稳的标志，其表达式如下：

(12)

式中，r为隧道半径；ν为泊松比；p0为外荷载；E为弹性模量。

3 数值模拟计算

3.1 数值计算方案

针对铁路隧道下穿既有公路隧道施工时引起围岩变形机理的量化分析，主要考虑围岩变形的各个影响因素的影响程度与影响机理。而围岩变形的影响因素很多，有些还相互影响。为了分析交叉隧道近接距离对围岩强度以及变形的影响，对不同近接距离下的隧道围岩变形值和应力值进行分析，以研究近接距离变化对围岩影响，采用对交叉隧道体系不同位置围岩进行监测的数值模拟方法。具体计算过程中，交叉隧道近接距离分别选取 2.5，5，10，20 m这4种，交叉隧道所在地层力学参数如表1所示。

表1 岩石力学基本参数

3.2 隧道模型建立

草莓沟2#隧道在下穿既有盘道岭公路隧道施工过程中采用的弧形导坑预留核心土的施工方法。为研究铁路隧道下穿既有公路隧道对围岩强度以及位移变化影响，以Mohr-Coulomb弹塑性准则为理论依据建立数值模图1为隧道数值模型图，模型尺寸为长×宽×高(100 cm×100 cm×160 cm)，上部覆土重度采用在模型顶面均布加载的方式。

三维数值模拟计算模型大小为：纵向沿高速公路段下穿隧道轴线方向取 60 m，水平边界长度约为隧道跨度的5 倍，长180 m; 垂直方向隧道底部以下25 m，上边界取近似地表的自由边界。模型左、右、前、后和下部边界均施加法向约束，地表为自由边界，计算简图如图1所示。

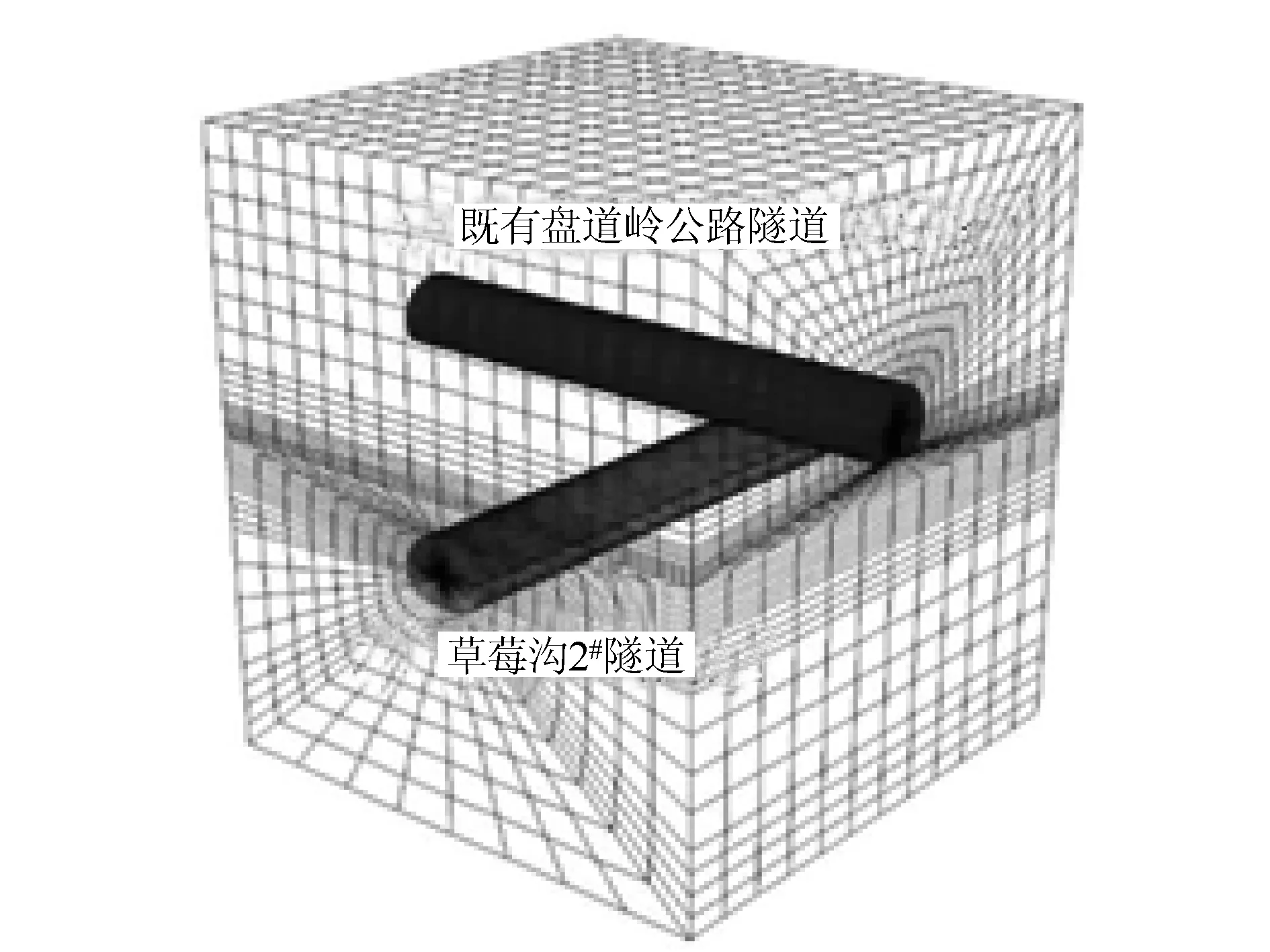
图1 计算模型力学参数对照Fig.1 Comparison of mechanical parameters obtained from calculation model

将表1模型参数代入Hoek-Brown计算公式后可得到围岩抗压强度和抗拉强度，同时利用闫长斌、徐国元和改进后的公式对3种不同隧道净间距下的围岩强度值进行估算，3种不同计算公式所得结果如表2所示。

表2 计算公式结果对照表

从表中可以看出随着净间距的增大，改进后的公式计算出的抗拉强度和抗压强度都有明显的增大，介于闫长斌、徐国元和广义Hoek-Brown取值之间，拱顶围岩位移值明显减小，其数值具有一定的合理性。Hoek-Brown强度修正公式考虑了交叉净间距影响，因此，在计算山岭交叉隧道近接交叉的岩体围岩参数时，利用修正后公式计算更能反映岩体的实际情况。令两隧道净间距为7.47 m，代入式(12)可以得到近接交叉段拱顶在无支护情况下的的围岩变形值为45.3 mm。

将表2模型参数带入Hoek-Brown计算公式后可得到围岩抗压强度和抗拉强度，同时利用闫长斌、徐国元和本文改进公式对3种不同隧道净距下的围岩强度值进行估算，3种不同计算公式所得结果如表3所示。

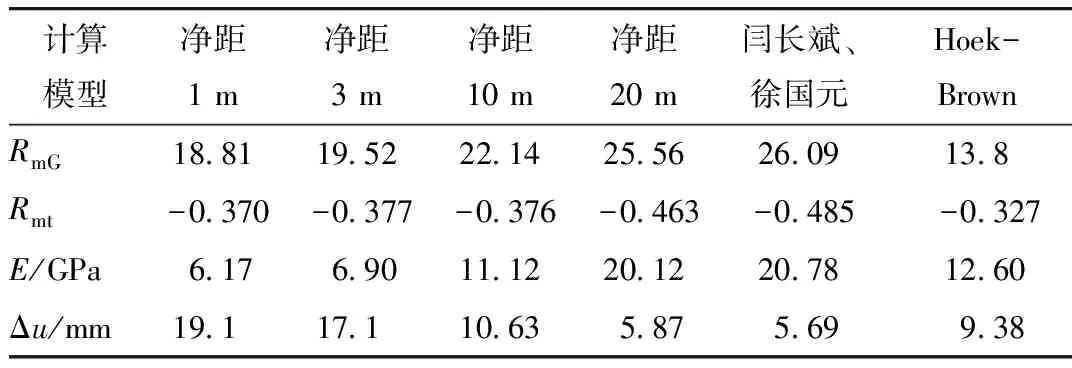
表3 计算模型力学参数对照表

从表中可以看出随着净距的增大，本文公式计算出的抗拉强度和抗压强度都有明显的增大，介于闫长斌、徐国元和广义Hoek-Brown取值之间，拱顶围岩位移值明显减小，其数值具有一定的合理性。

4 计算结果对比分析

同时为了验证分析的科学性，对隧道交叉段围岩利用全站仪进行拱顶变形监测，具体方法为：在监测断面拱顶悬挂水准尺，远处设置基准点(选在距测量点100 m远处无下沉的点)，采用二等水准仪对两位置读数做差得到拱顶的相对高程，进行数据处理，得出隧道交叉段各测点围岩相对位移变化情况。以里程JDLDK01+405为起点每隔10 m取1个监测断面，共取4个断面。由于在实际工程中，不可能改变隧道的近接距离来测得不同接近距离下的相互影响程度，根据4个断面与上部隧道空间距离不同，由这4个测点距交叉点不同的水平距离来反映4种不同近接距离下的影响程度，4个测点位置拱顶下沉测量结果处理后绘制成曲线如图2(a) 所示。

图2 修正公式前后对比图Fig.2 Comparison of results obtained from formulas before and after correction

从图2(b)～(d)可以看出随着净距增大，围岩变形越来越小，计算结果与实际测量结果相符，本文的Hoek-Brown强度修正公式考虑了交叉净距影响，因此，在计算山岭交叉近接隧道的岩体围岩参数时，利用本文修正后公式计算更能反映岩体的实际情况。

5 结论

(1)在众多岩体力学参数的换算方法中，Hoek-Brown公式和其他对Hoek-Brown 公式的修正公式虽然考虑因素比较全面，发展比较完善，但在山岭立体交叉近接隧道情况下，都未能考虑净距对围岩参数影响，这些方法均不能计算出隧道交叉情况下的围岩参数。

(2) 通过对盘道岭与草莓沟1#线交叉隧道围岩变形进行研究，发现随着两隧道净距越小，围岩变形越大。

(3)利用广义Hoek-Brown 公式、闫长斌，徐国元修正公式、Hoek-Brown 修正公式和本文的修正公式分别对交叉隧道围岩强度进行求解，将计算结果与现场测量进行了对照，发现监测结果与本文改进后的公式计算结果符合，进一步说明了本文改进公式的合理性。

(4)此修正公式的提出是对Hock-Brown强度准则新内涵的探索，表明了交叉隧道围岩力学参数与两隧道净距的关系，同时也为今后交叉隧道力学研究提供了工程参考和理论依据。

[1] 闫长斌，徐国元. 对Hoek-Brown公式的改进及其工程应用[J].岩石力学与工程学报，2005，24(22)：4030-4035.

YAN Chang-bin，XU Guo-yuan. Modification of Hoek-Brown Expressions and Its Application to Engineering [J].Journal of Rock Mechanics and Engineering, 2005, 24(22)：4030-4035.

[2] 李胡生, 熊文林.岩石力学参数的工程模糊处理[J]. 水利学报,1994，1：76-85. LI Hu-sheng，XIONG Wen-lin. Engineering Fuzzy Treatment of Mechanical Parameters of Rock[J]. Journal of Hydraulic Engineering，1994，1：76-85.

[3] MANEV G, AVRAMOVA-TACHEVA E. On the Valuation of Strength and Resistance Condition of the Rock in Natural Rock Mass[C]//Proceedings of the Second Congress of the International Society for Rock Mechanics. Belgrade：Yugoslavian Science Press，1970: 365-374.

[4] HOEK E. Practice Rock Engineering[M]. Rotterdam：Ellis Horwood,2000.

[5] 张建海, 何江达, 范景伟. 小湾工程岩体力学参数研究[J]. 云南水力发电, 2000，16(2)：1458-1466. ZHANG Jian-hai，HE Jiang-da，FAN Jing-wei. Rock Mechanical Parameter Study of Xiaowan Project [J].Yunnan Hydropower, 2000，16(2)：1458-1466.

[6] 孙金山, 卢文波. Hoek-Brown经验强度准则的修正及应用[J]. 武汉大学学报：工学版，2008，41(1)：63-66,124. SUN Jin-shan，LU Wen-bo. Modification of Hoek-Brown Criterion and Its Application [J]. Engineering Journal of Wuhan University，2008，41(1): 63-66,124.

[7] HOEK E, CARRANZA-TORRES C. Hoek-Brown Failure Criterion: 2002 ed[C]// Proceedings of the Fifth North American Rock Mechanics Symposium. Toronto：University of Toronto Press，2002：267-271.

[8] 石明霞, 谭文, 吉小明. 大跨隧道临时支护拆除及二次衬砌施工数值模拟分析[J]. 公路交通技术, 2009(5):106-110. SHI Ming-xia, TAN Wen, JI Xiao-ming. Numerical Simulation Analysis of Removal of Temporary Supporting and Construction of Secondary Lining of Large-span Tunnel[J]. Technology of Highway and Transport, 2009(5):106-110.

[9] 沈荣明, 陈建峰. 岩体力学[M].上海：同济大学出版社，2006:114-115. SHEN Rong-ming，CHEN Jian-feng. Rock Mass Mechanics [M].Shanghai：Tongji University Press，2006:114-115.

[10]HOEK E，BROWN E T. Practical Estimates of Rock Mass Strength[J]. International Journal of Rock Mechanics & Mining Sciences，1997，34(8): 1165-1186.

[11]HOEK E. Strength of Jointed Rock Masses, 23rd Rankine Lecture[J]. Géotechnique, 1983, 33 (3): 187-223.

A Method for Calculating Surrounding Rock Parameters of Close-spaced Crossing Tunnel Based on Hoek-Brown Strength Criterion

XIE Bao-jin1, 2，ZHANG Xiang-dong1

(1.School of Civil Engineering and Transportation, Liaoning Technical University, Fuxin Liaoning 123000, China;2. The Third Engineering Co., Ltd., of China Railway Seventh Group, Xi’an Shaanxi 710000,China)

To use Hoek-Brown strength criterion which has a wide using range in the engineering field, it must be amended to make it suitable for calculating the anisotropy rock mechanical parameters. Considering the influence of clear distance of crossing tunnel on the strength of surrounding rock comprehensively, the relation between disturbance coefficient and clear distance in Hoek-Brown strength criterion is quantified, and the revised Hoek-Brown formula under the influence of different clear distances of up-down tunnels is obtained through theoretical derivation and numerical checking calculation. The result calculated by the modified strength formula coincides with the measured data, which indicates that the revised Hoek-Brown strength formula can better reflect the real deformation conditions of the surrounding rocks of crossing tunnels.

tunnel engineering; close-spaced crossing tunnel；modeified Hoek-Brown strength formula; theoretical derivation; amend

2016-05-06

国家自然科学基金委员会-神华集团有限公司煤炭联合基金项目(51174268);辽宁省自然科学基金项目(201202095)

谢宝琎(1975-)，男，甘肃白银人，博士，高级工程师.(2444606539@qq.com.)

10.3969/j.issn.1002-0268.2016.12.016

U451.2

A

1002-0268(2016)12-0101-05