一种生物证书密钥生成算法
王金海, 魏 宁, 崔 军, 李雪妍, 李秀艳
(天津工业大学 电子与信息工程学院, 天津 300387)
一种生物证书密钥生成算法
王金海, 魏 宁, 崔 军, 李雪妍, 李秀艳
(天津工业大学 电子与信息工程学院, 天津 300387)
生物特征数字证书涉及的RSA公私钥对可以由近似随机信号的生物特征密钥派生,但是生物特征密钥长度较短,而基于大素数分解困难的RSA算法要求密钥较长. 为了解决该问题,提出一种生物证书密钥生成算法,结合对称加密算法和大素数生成算法生成生物大素数,并采用哈希算法对生物大素数进行可用性设计,在解决密钥长度问题的同时保证生物大素数安全可用,以便用于生成生物特征数字证书中的RSA公私钥对. 基于VC6.0和MIRACL大数库的实验结果表明:基于生物特征密钥生成的生物大素数满足确定性和可用性,能够应用于生物数字证书之中. 本文所提算法行之有效,且具有实际应用价值.
生物特征加密; 生物证书; 生物特征密钥; RSA; 大素数
近年来,快速发展的生物特征加密技术越来越实用化,其应用到数字证书的研究与日俱增[1-3]. 文献[4]于2007年提出了生物证书的概念,把生物证书定义成CA颁发的绑定了用户身份及其生物特征信息并经过CA签名的数据结构. 国内学者提出了一种基于生物属性证书的生物认证系统,进一步推动了生物特征与数字证书的结合研究[5-6].
事实上,基于原始生物特征数据直接或间接生成的生物特征密钥(简称BioKey,生物密钥)是指一个稳定的近似随机的二进制序列[7]. 它的长度是相对有限的,一般为百位左右比特量级[8],如Nandakumar[9]使用指纹库FVC2002-DB2基于指纹Fuzzy Vault生成的BioKey长度为128 bits, George S. Eskander[10]基于各种生物特征使用Fuzzy Vault算法生成的各生物特征的密钥熵为69 bits. 而数字证书对密钥是有一定要求的,主要体现在RSA算法对密钥的要求上. RSA算法是基于“对于两个大素数p和q,计算它们的乘积n(n的二进制位数即为密钥长度)十分容易,但要对n进行因式分解得到p和q却极其困难”的思想,将乘积n公开,作为公开密钥. RSA算法的安全性依赖于大素数n被分解的难度. 在实际应用中,为保证加密的安全性和可靠性,RSA算法要求大素数p和q均为512 bits,即RSA的密钥长度为1024 bits[11].
针对长度较短的BioKey无法满足数字证书中RSA算法对密钥要求的问题,目前相关探讨较少,仅在2012年,Vincenzo[12]提出了一种基于生物特征密钥利用映射表生成RSA公私钥对的方法,但是该文献没有详细描述如何构造映射表以及进一步评估论证派生的大素数p和q是否安全可用和唯一确定. 而且注意到,这个映射表中大素数的个数是2n,是相对有限的,这样肯定导致不同BioKey映射成相同大素数p和q的碰撞概率较大. 但是通过增大2n值来降低碰撞概率显然是不可取的,因为存储映射表的智能卡存储空间是有限的. 假设这个映射表里有100 000个512 bits的大素数,那么就要求智能卡的容量至少达到64 MB,而这个量级的存储容量是当前一般智能卡所不支持的.
因此,对基于较短BioKey构造出长度相对较长的BioRSA大素数p和q(简称BioPrimes,生物大素数)的密钥扩散问题进行研究是很有必要的. 如何由BioKey生成BioPrimes是本文拟解决的首要问题,当然,在此基础上,生成的BioPrimes还应满足确定性(即同一个BioKey每次都会确定生成同一个BioPrimes)和可用性(即生成的BioPrimes可以无差错地应用到RSA算法中). 因此,本文除了研究BioPrimes生成方法之外,还需要对生成的BioPrimes做关于可用性和确定性的设计与验证.
针对以上问题,本文基于长度较短的BioKey提出一种RSA大素数生成方法,即由BioKey构造出长度相对较长的BioRSA大素数p和q,即BioPrimes.
1 RSA算法和大素数生成算法
1.1 RSA算法
RSA算法是一种典型的公钥密码算法,具有公开密钥和私有密钥两个紧密相关但却不同的密钥,即公钥和私钥:1)公钥可以公开给任何人,用于加密数据(仅对应的私钥能解密),或验证签名(对应私钥进行签名);2)私钥不能公开,必须安全保存. RSA算法的理论基础是一种特殊的可逆模指数运算,它的安全性基于分解大素数n的困难性,其算法描述如下[13]:
1)独立地选取两个大素数p和q(保密),计算n=pq(公开),φ(n)=(p-1)(q-1)(保密),其中φ(n)是欧拉函数;
2)选取一个整数e,满足1≤e<φ(n),且gcd(φ(n),e)=1,其中gcd()表示求最大公约数;
3)计算d(保密),满足ed=1mod φ(n),即d是e在模φ(n)下的乘法逆元;
4){e,n}为公钥,{d,n}为私钥,p和q则丢弃.
假设要加密的明文为M,密文为C,则加密过程为C=E(M)=Me(mod n),解密过程为M=D(C)=Cd(mod n).
RSA算法中的p、q、φ(n)和d是秘密保存的,只有私钥拥有者才知晓. 如果要对RSA算法加密后的密文进行破译,唯一可能的破解方法就是对公钥{e,n}中的n进行因子分解. 对于大素数的因子分解,分解次数与其长度有关,随着密钥长度的增加,分解所需的时间就会成指数增加,密钥就越难破译,加密强度就越高.
由此可见,要使RSA加密的数据安全可靠,关键是生成两个满足长度要求的大素数p和q. RSA加解密算法的安全性与其所使用的大素数有密切关系,构造符合RSA安全体系要求的大素数是RSA算法实用化的基础. 因此,针对生物特征密钥与公钥数字证书的结合应用,研究基于较短BioKey生成较长BioPrimes,对BioRSA算法的安全性具有实际应用价值.
1.2 大素数生成算法
素数生成的核心问题是判断一个数是否为素数. 目前,生成素数的一般方法可以分为两类,即确定性素数生成算法和概率性素数生成算法.
确定性素数生成算法是指其生成的数一定是素数. 在确定性素数生成算法中,素数是按照一定公式或者能够满足素数充分必要特性的规则进行素数生成. 现有的确定性素数生成算法有许多,其中比较有代表性的是AKS算法[14]. 这类算法的优点是生成的必然是素数,但却带有一定的限制. 假若算法设计不佳,便容易构造出带有规律性的素数,攻击者能够分析出素数的变化,进而可以猜到该系统中使用的素数. 另外确定性素数生成算法运行耗时太长,因此在实际应用中较少采用.
概率性素数生成算法与确定性素数生成算法的最大不同是其生成的数可能是伪素数,尽管其生成合数的可能性很小,但不能为0. 此类方法缺点明确,即存在误判的可能性;优点也很明显,就是生成速度较快,生成的素数无规律. 概率性素数生成算法是当前素数生成的主要方法,其中较为著名的算法有Miller-Rabin算法[15]等.
本文以这两种大素数生成算法为基础,通过合理设计与验证,选择实用的大素数生成算法,实现生物大素数生成.
2 一种生物证书密钥生成算法
如何由长度相对较短的BioKey构造出确定的BioPrimes,进而保证其真正可用,最终生成BioRSA公私钥对并应用于证书中,本文将给出一种基于生物特征的生物证书密钥生成算法,该方法分为注册和验证两个阶段.
2.1 注册阶段
注册阶段旨在基于由生物特征图像利用Fuzzy Vault算法生成的128 bits BioKey间接构造出可用于RSA算法中的512 bits BioPrimes. BioKey应用于BioRSA时必须保证其可用性,即保证生成的BioPrimes可以无差错地应用到RSA算法中. 可能的问题点:1)在验证阶段,BioKey恢复时并不能保证与注册时生成的BioKey完全相同;2)在生物大素数生成方法中,不同的素数生成算法会导致BioPrimes的生成概率不一定是百分之百,即不能完全保证同一个BioKey每次都会确定生成同一个BioPrimes. 所以,最终得到的BioPrimes并不一定能用于生成BioRSA公私钥对. 本文采用哈希算法解决这两个问题.
哈希算法[16]是将任意长度的二进制值映射为较短的固定长度的二进制值,这个小的二进制值称为哈希值. 哈希值是一段数据唯一且极其紧凑的数值表示形式. 如果修改一段明文而且哪怕只更改该段落的一个字母,随后的哈希都将产生不同的值. 要找到哈希值相同的两个不同的输入,在计算上几乎是不可能的. 目前比较常用的哈希算法是MD5和SHA-1.
参照图1,注册阶段具体包含以下几个步骤:
1)输入128 bits 注册BioKey,并对其做随机数测试[17],以保证BioKey为近似随机数;
2)将通过随机数检测的注册BioKey做哈希运算,得到注册BioKey的哈希值;
3)随机产生两个512 bits通过随机数测试的随机数因子;
4)将BioKey作为对称加密算法(如AES[17])密钥用来加密两个随机数因子,得到两个帮助数据;
5)将BioKey分别与两个随机数因子异或,异或后的值利用大素数生成方法生成512 bits BioPrimes;
6)512 bits BioPrimes一方面通过哈希运算得到生成BioPrimes的哈希值,另一方面进行BioRSA公私钥对生成,以便用于证书中.
通过上述步骤,128 bits的近似伪随机数BioKey首先间接生成512 bits大素数BioPrimes,然后再由BioPrimes生成公私钥对,其中,在注册阶段得到的帮助数据和两个哈希值均保存起来在验证阶段辅助恢复出BioRSA公私钥对. 需要注意的是,由于素数生成算法有确定性生成和概率性生成之分,前者可给出确定的结果但通常较慢,后者则反之. 因此,本文后面实验部分将通过仿真实验,针对运算性能和确定性,对确定性生成算法和概率性生成算法进行实用性评估,以选择实用的素数生成算法为本文方法所用.

图1 注册阶段
2.2 验证阶段
验证阶段过程与注册阶段过程最大的不同体现在:1)通过解密帮助数据得到随机数因子;2)通过两次比较哈希值以保证恢复的BioPrimes可用于恢复BioRSA公私钥对.
流程图如图2所示,具体步骤如下:
1)输入128 bits验证BioKey,并对其做随机数测试;
2)对通过随机数检测的验证BioKey做哈希运算,得到验证BioKey的哈希值;
3)对比注册BioKey与验证BioKey的哈希值,若相等转步骤4),否则需重新输入验证BioKey;
4)将注册BioKey作为对称加密算法密钥用来解密帮助数据,恢复出随机数因子;
5)恢复出的随机数因子与验证BioKey异或后利用大素数随机数方法恢复出512 bits BioPrimes;
6)512 bits BioPrimes通过哈希运算,得到恢复BioPrimes的哈希值;
7)对比生成BioPrimes与恢复BioPrimes的哈希值,若相等则基于该BioPrimes恢复BioRSA公私钥对,否则需重生成BioPrimes.
步骤3)中,若注册BioKey与验证BioKey的哈希值相等,则说明验证BioKey与注册BioKey完全相同,保证了BioKey的可用性;步骤7)中,通过对比生成BioPrimes与恢复BioPrimes的哈希值,保证了同一个BioKey每次都会确定生成同一个BioPrimes,即保证了BioPrimes的可用性. 当然,如果连续多次(例如3次)哈希值对比失败,则可以认为不是同一个BioKey导致,验证阶段异常终止.

图2 验证阶段
3 实验验证与结果分析
针对BioPrimes素数生成算法选择实验、确定性验证实验和可用性验证实验进行详细阐述,根据实验结果选择合适的素数生成算法,并做确定性和可用性验证评估.
本文的算法均采用C++语言在VC6.0和MIRACL大数库仿真环境下实现. MIRACL大数库(Multiprecision Integer and Rational Arithmetic C/C++ Library)是由Shamus Software Ltd.开发的关于大数运算函数库,用来设计与大数运算相关的密码学之应用. 本文主要用到MIRACL库中isprime函数、nxprime函数、AES加解密函数和SHA-1哈希函数等. 3.1 生物大素数生成算法选择实验
分别选用AKS算法和Miller-Rabin算法作为生物大素数生成方法中的确定性、概率性素数生成算法. 如果选择AKS算法生成生物大素数,理论上同一个BioKey每次都会确定生成同一个BioPrimes,需要检验其运算性能是否符合实用要求;如果选择Miller-Rabin算法,则还需要进一步验证其理论上的不确定性在实际中体现为多少. 因此本文先实验对比这两种算法生成的素数和运算性能(指时间消耗),从实用性角度选择合适的素数生成算法来辅助生成BioPrimes.
由于MIRACL函数库已用isprime函数对Miller-Rabin算法进行封装,故本文仅需调用isprime函数做Miller-Rabin算法素性判断即可.
先随机生成一个n bits的二进制数p并设高低位为1,高位设为1是为了保证随机数的位数,低位设为1是为了过滤掉偶数. 然后,分别利用AKS算法和Miller-Rabin算法(isprime函数)对p进行素数判定,若p是素数则输出p和运行时间,反之p自加2再进行素数判定,直到找到比p大的第一个素数(流程图见图3). 记录分别用这两种方法找到的n bits素数p和其运行所需时间,然后对比分析数据确定选用何种算法辅助生成BioPrimes.
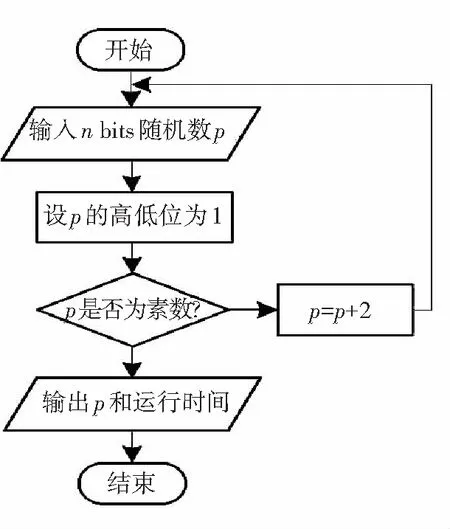
图3 生物大素数生成算法选择实验流程图
Fig.3 Flowchart of the selection of BioPrimes generation algorithm
根据图3,编写调试C++程序,并以表格形式给出分别用AKS算法和Miller-Rabin算法(isprime函数)找到的n bits素数p与运行所需时间的数据结果(见表1).
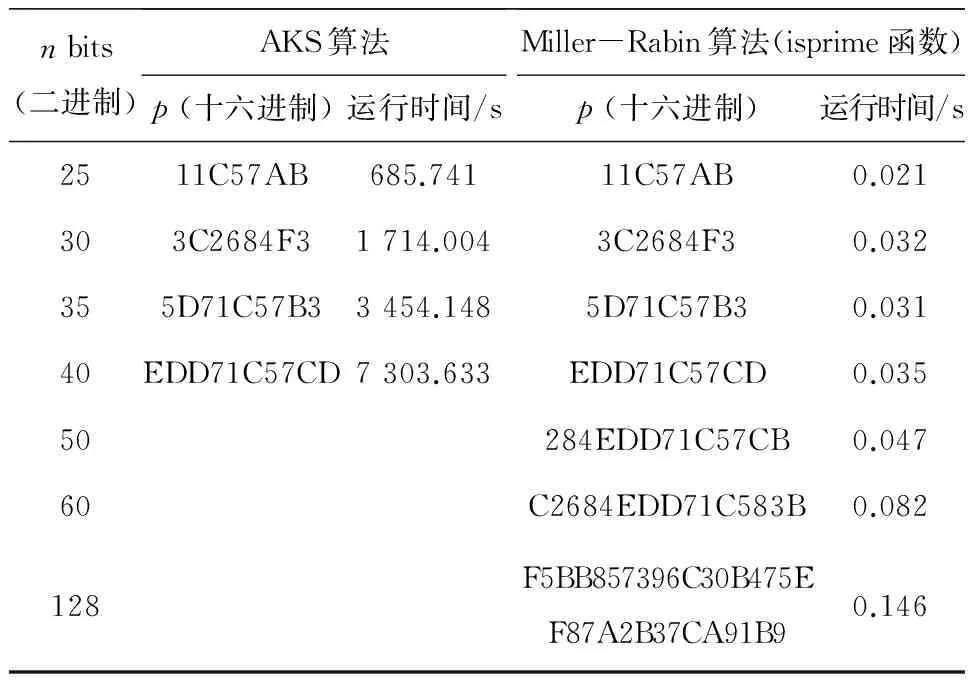
表1 AKS算法和Miller-Rabin算法对比
由表1的前四行可以看出,当n一定时,利用AKS算法和Miller-Rabin算法(isprime函数)产生的素数相同,但运行时间却相差很大. 如当n为40时,利用AKS算法找到素数EDD71C57CD的时间为7 303.633 s(约为121.73 min),而利用Miller-Rabin算法(isprime函数)找到的素数相同,运行时间却是0.035 s. 当n>40 bits时,AKS算法素数生成整个过程消耗的时间将不可估量,而利用Miller-Rabin算法(isprime函数)生成128位素数仅需0.146 s. 理论上,AKS算法的时间复杂度是O((logn)),而Miller-Rabin算法的时间复杂度是O((logn)/7),这一实验结果也验证了二者的时间复杂度问题. 所以,AKS算法由于时间消耗问题并不适合大整数的素性检测,故选用Miller-Rabin算法(isprime函数)作为本文所提生物大素数生成方法中的素数生成算法.
3.2 生物大素数确定性验证实验
由于Miller-Rabin算法属于概率性素数生成算法,在其素数判断过程中可能会误判,所以需要进一步验证其理论上的不确定性在实际中体现为多少,即解决保证同一个BioKey每次都会确定生成同一个BioPrimes(即确定性)问题.
进行多次测试,将每次针对同一BioKey生成的BioPrimes'与第一次生成的BioPrimes对比,以表格形式统计记录实验结果(见表2),探究其确定生成的概率.
由表2可知,通过把多次测试的数据与第一次生成的BioPrimes做对比,可认为在一定测试次数范围内,同一BioKey确定生成同一BioPrimes的概率为100%,即认为采用Miller-Rabin算法(isprime函数)作为素性检测算法生成BioPrimes满足确定性. 与128 bits BioKey相比,第一次生成的BioPrimes长度变为512 bits,但是该方法并没有改变其随机特性,BioPrimes依然是随机数.
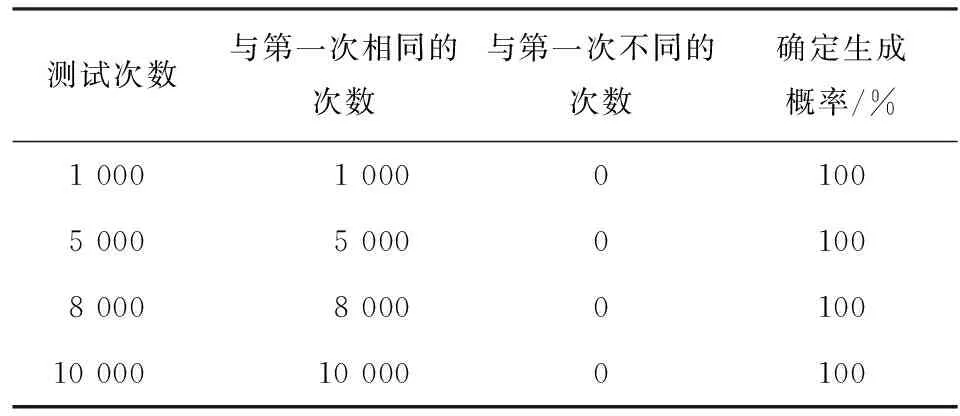
表2 多次测试统计结果
3.3 生物大素数可用性验证实验
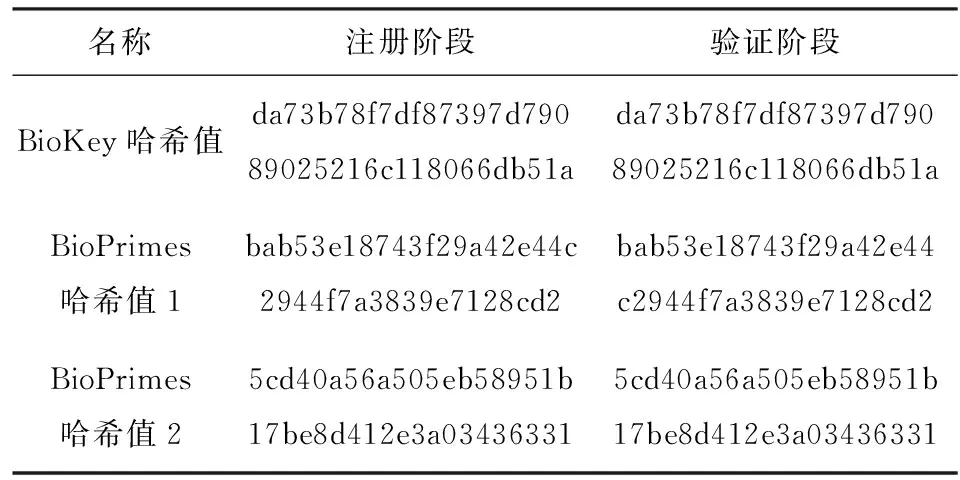
上述实验中,若超出测试范围,BioPrimes的确定生成概率可能达不到100%,本文通过哈希值对比对其做了可用性设计,以保证即使BioPrimes的确定生成概率不为100%,它也可以用于生成BioRSA公私钥对. 在注册与验证阶段得到的哈希值如表3所示.
表3 注册与验证阶段哈希值对比
Tab.3 Comparison of the hash value of registration and verification phase
名称注册阶段验证阶段BioKey哈希值da73b78f7df87397d79089025216c118066db51ada73b78f7df87397d79089025216c118066db51aBioPrimes哈希值1bab53e18743f29a42e44c2944f7a3839e7128cd2bab53e18743f29a42e44c2944f7a3839e7128cd2BioPrimes哈希值25cd40a56a505eb58951b17be8d412e3a034363315cd40a56a505eb58951b17be8d412e3a03436331
注:注册阶段和验证阶段的运行时间分别为1.920和1.561 s
从表3可以看出,注册与验证阶段BioKey的哈希值相等,说明在验证阶段恢复出的BioKey与注册时生成的BioKey完全相同. 通过对比表3中注册阶段与验证阶段生成的BioPrimes的哈希值,发现它们各自相等,说明生成的BioPrimes可用于生成BioRSA公私钥对. 注册阶段与验证阶段的运行时间均不到2 s,说明本文所提方法行之有效. 另一方面,基于哈希算法和对称加密算法的安全性,表3中的这3个哈希值以及注册阶段得到的帮助数据可以安全公开,同时也避免了文献[12]中存在的把映射表存储在智能卡引起的存储容量问题.
以上结果表明,基于BioKey能够生成满足随机性、确定性和可用性要求的BioRSA公私钥对应用于生物证书中,本文提出的生物证书密钥生成算法是有实用价值的.
4 结 语
通过研究生物特征密钥应用到公钥数字证书的趋势,针对生物特征密钥BioKey的长度无法满足基于时间复杂度的RSA算法对素数的要求的问题,提出一种生物证书密钥生成算法. 通过哈希算法、对称加密算法和大素数生成方法,128 bits生物特征密钥BioKey能够生成512 bits生物大素数BioPrimes,进而生成BioRSA公私钥对,最终可应用于生物证书中. 基于VC6.0和MIRACL大数库实验选择合适的素数生成算法,并对BioPrimes做确定性和可用性验证与评估. 本文所提方法简单、易实现,满足RSA算法安全性的实际应用需求,实现了从BioKey到BioRSA的映射,为生物特征密钥应用到数字证书提供了极大的便利.
[1] LAKAHMI A J, KIRAN P S. PKI key generation based on multimodal biometrics[J]. International Journal OfComputers & Communications, 2012, 1(1): 9-16.
[2] KALAMA A E, IBJAOUN S, OUAHMAN A A. Biometric authentication systems based on hand pattern vein, digital certificate and smart cards[C]// Security Days, 2013 National. Rabat: IEEE, 2013: 1-8.
[3] WANG W, LU Y, FANG Z. Biometric template protection based on biometric certificate and fuzzy fingerprint vault[C]// Advanced Data Mining and Applications. Hangzhou: Springer Berlin Heidelberg, 2013: 241-252.
[4] CHUNG Y, MOON K, LEE H W. Biometric certificate based biometric digital key generation with protection mechanism[C]// Frontiers in the Convergence of Bioscience and Information Technologies. Washington DC: IEEE Computer Society, 2007: 709-714.
[5]李超, 辛阳, 纽心忻, 等. 一种基于生物证书的身份认证方案[J]. 计算机工程, 2007, 33(20): 159-161.
LI Chao, XIN Yang, NIU Xinxin, et al. Identity Authentication Scheme Based on Biometric Certificate[J]. computer engineering, 2007, 33(20): 159-161.
[6]辛阳, 魏景芝, 李超, 等. 基于PKI和PMI的生物认证系统研究[J]. 电子与信息学报, 2008, 30(01): 1-5.
XIN Yang, WEI Jingzhi, LI Chao, et al. Research on the Telebiometric Authentication System Based on PKI and PMI[J]. Journal of Electronics and Information Technology, 2008, 30(01): 1-5.
[7]陈熙. 鉴别生物特征提取及密钥生成研究[D]. 成都:西南交通大学, 2011.
CHEN Xi. Research on discriminative biometrics feature extraction and key generation[D]. Chengdu:Southwest Jiaotong University, 2011.
[8] RATHGEB C, UHL A. A survey on biometric cryptosystems andcancelable biometrics[J]. EURASIP Journal on Information Security, 2011, 3(1): 1-25.
[9] NANDAKUMAR K, JAIN A K, PANKANTI S. Fingerprint-based fuzzy vault:Implementation and performance[J]. IEEE Transactions on Information Forensics and Security, 2007, 2(4): 744-757.
[10]ESKANDER G S, SABOURIN R, GRANGER E. A dissimilarity-based approach for biometric fuzzy vaults-application to handwritten signature images[C]// New Trends in Image Analysis and Processing-ICIAP 2013. Naples: ICIAP 2013 International Workshops, 2013: 95-102.
[11]刘新星, 邹潇湘, 谭建龙. 大数因子分解算法综述[J]. 计算机应用研究, 2014, 31(11): 3201-3207.
LIU Xinxing, ZOU Xiaoxiang, TAN Jianlong. Survey of large integer factorization algorithms[J]. Application Research of Computers, 2014, 31(11): 3201-3207.
[12]CONTI V, VITABILE S, SORBELLO F. Fingerprint traits and RSA algorithm fusion technique[C]// Complex, Intelligent and Software Intensive Systems (CISIS). Palermo: IEEE, 2012: 351-356.
[13]RSA(cryptosystem) [EB/OL].
[2014.11]. http://en.wikipedia.org/wiki/RSA_(cryptosystem).
[14]AGRAWAL M, KAYAL K, SAXENA N. Primes is in P[J]. Annals of Mathematics, 2004, 160(2): 781-793.
[15]龙建超. 公钥算法中大素数生成方法的研究与改进[D]. 昆明: 云南大学, 2014.
LONG Jianchao. Research and improvement on the method of generating large prime number in public key algorithm[D]. Kunming: Yunnan University, 2014.
[16]STALLINGS W.密码编码学与网络安全:原理与实践[M]. 王张宜, 杨敏, 杜瑞颖, 等, 译. 北京: 电子工业出版社, 2012: 104-131, 236-257.
STALLINGS W. Cryptography and NetworkSecurtiy: Principles and Practice[M]. Bei Jing: Electronic Industry Press, 2012: 104-131, 236-257.
[17]NIST SP800-22. A statistical test suite for random and pseudorandom number generators for cryptographic applications[S]. Gaithersburg: ITLB, 2001.
(编辑 王小唯 苗秀芝)
Biometric certificate key generation algorithm
WANG Jinhai, WEI Ning, CUI Jun, LI Xueyan, LI Xiuyan
(School of Electronic and Information Engineering, Tianjin Polytechnic University, Tianjin 300387, China)
The RSA public and private keys of biometric certificate can be generated from biometric key which can be seen as random numbers.However, the size of biometric key is shorter than the RSA public and private keys. To overcome this limitation, a biometric certificate key generation algorithm is proposed. In this method, the biometric primes is generated by the combination of symmetric key encryption algorithm and prime generation algorithm, in addition, the hashing algorithm is used to ensure the feasibility of the biometric primes. The generated biometric primes are safe and usable so that they can be applied to generate the RSA public and private keys of biometric certificate. Experimental results using VC6.0 and MIRACL show that the proposed method not only is feasible, but also has practical application value.
biometric encryption; biometric certificate; biometric key; RSA; big primes
10.11918/j.issn.0367-6234.2016.11.014
2015-06-29
天津市高等学校科技发展基金计划项目(20140805)
王金海(1966—),男,博士,教授
崔 军,cuijunlq@126.com
TP309.2
A
0367-6234(2016)11-0090-06

