高性能滚珠丝杠副有限元热分析
陈婉,王科社,宋杰,董青霞
北京信息科技大学,北京,100192
高性能滚珠丝杠副有限元热分析
陈婉,王科社,宋杰,董青霞
北京信息科技大学,北京,100192
结合热传递的相关知识,计算滚珠丝杠副丝杠、轴承以及电机三种热源的发热量及边界对流系数。利用有限元分析软件对滚珠丝杠副进行温度场仿真分析,发现温升近似与转速成正比且电机的温升最高。进而对各部分热源的温升情况进行实验验证,证明了仿真结果的正确性。在此基础上,对滚珠丝杠副进行热变形分析,得出热变形及热应力分布云图。分析转速与初始温度对热变形的影响,结果表明,转速越大,初始温度越高,热变形量越大,且热应力主要集中在丝杠两端,中间部分的热应力分布比较均匀,应力较小。
滚珠丝杠;温度场;热变形;有限元分析
0 引言
滚珠丝杠副作为一种高精度传动部件,在正常工作条件下,各种热源会产生大量的热,这些热量通过热传导、热辐射等方式传给机床的各个部件,引起热变形,从而影响系统精度[1]。
目前,国内外对滚珠丝杠温度场的分析已取得一定成果,但大都未考虑电机这个发热源。本文在已有研究的基础上,加入电机发热,得出不同转速及不同初始温度下各部分的温升情况,并进行实验验证,进而利用ANSYS分析得出转速及初始温度对滚珠丝杠副热特性的影响规律。
1 滚珠丝杠副发热量的计算
1.1 热分析基础
热量传递的基本方式有三种:热传导、热对流和热辐射[2]。
滚珠丝杠副的发热量主要是由摩擦热产生的,因为空气对流,一部分热散发出去,同时润滑剂的冷却作用也会带走一部分热量,剩余部分热量则会导致丝杠副的温度上升,进而产生热变形[3],影响滚珠丝杠的精度。
对于滚珠丝杠热变形的分析,主要的问题在于热源和热传递方式。滚珠丝杠副的热源主要为滚珠、丝杠和螺母之间的摩擦生热、轴承产生的摩擦热以及电机发热。由于滚珠丝杠副热辐射的影响很小,因此热传递方式则主要为热传导和热对流。
1.2 发热量计算
滚珠丝杠传动系统的发热主要是由摩擦引起的,可以分为以下三部分[4]:
(1)滚珠丝杠副热量计算
滚珠丝杠副发热量可根据轴承的计算公式[2]来计算:

式中,n为丝杠转速(r/min),M为滚珠丝杠副的总摩擦力矩(N·mm)。
(2)轴承热量计算
轴承发热量的计算公式如下所示:Q=1.047×10-4nM(W) (1.2)
式中,n为丝杠转速(r/min),M为滚珠丝杠副的总摩擦力矩(N·mm)。
(3)电机热量计算
电机的热传导很复杂,传入机座的热量也因机座结构的不同而不同,其发热量计算公式如下:

式中H为发热量(KW),为电机输出力矩(N·m),η是电机的机械效率。
根据公式(1.1)、(1.2)、(1.3)可计算出不同转速下滚珠丝杠副系统的各处热源,根据热源及热传递相关公式可计算出加载的热流密度,结果如表1所示。

表1 各热源、热流密度计算结果Tab.1 calculation results of heat source and heat flux
2 边界条件的计算
边界条件是指导热物的表面传热情况或者边界处的温度[5]。
2.1 丝杠对流边界条件
滚珠丝杠副运动的过程属于强迫对流,由努谢尔特准则[6]可知,强迫对流时,当主轴以一定的速度旋转时,和空气的对流换热系数的计算公式如下:

式中,Nu是努谢尔特系数,λ是流体热传导系数[W/(m·K)],d是当量直径(m),Re是雷诺数,Pr是普朗特数。
初始环境温度为20℃时,空气物理性质参数为:导热系数λ=2.59310-2W/(m·K);运动粘度ν=1.81×10-5;普朗特数Pr=0.703。
丝杠转速 n=1500r/min,根据式(2.1)、(2.2)、(2.3)计算丝杠与空气之间的对流参数:
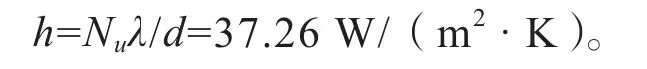
同理,当转速改变时,可根据式(2.1)、(2.2)、(2.3)计算不同转速下丝杠的对流系数。
3.2 轴承、电机边界对流条件
滚珠丝杠运动过程中,轴承支座,螺母外圈,电机机壳,在丝杠传动过程中处于静止状态,因此,他们与空气的对流的计算采用大空间对流公式[7]:

式中C是对流放热系数,Gr是格拉晓夫数,λ是空气导热系数,α是空气热膨胀系数,α=1/T;T是热力学温度。
根据公式(2.4)、(2.5),可分别计算出轴承和电机座的边界对流条件。
轴承边界对流条件:
Gr=1.89×105;
Gr·Pr=1.89×105×0.703=1.328×105;
根据Gr·Pr的适用范围,查表2得C=0.59,n=1/4。代入公式(2.4)得努谢尔特数:
Nu=C(Gr·Pr)n=0.59×(1.328×105)1/4=11.26;h=(Nuλ)/d=6.95 W/(m2·K)。
(2)电动机边界对流条件:
Gr=4.6×105;
Gr·Pr=4.6×104×0.703=3.23×105;
查表2得:
C=0.59,n=1/4;则Nu=14.065;
h=9.12 W/(m2·K);
以上得出的是理论边界对流系数,在实际分析中,采用的对流系数是理论值的3~10倍,因此得出各处的对流边界值如表3所示。

表3 边界对流系数Tab.3 Boundary convection coefficient
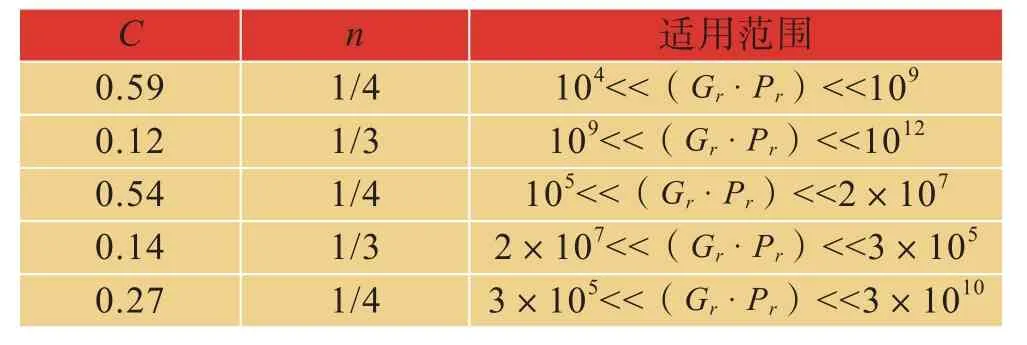
表2 对流放热系数表Tab.2 convective heat transfer coefficient
3 滚珠丝杠副温度场仿真分析
3.1 建模与网格划分
根据北京精密天工有限公司提供的滚珠丝杠的参数,建立简化的三维模型并进行网格划分,网格划分方式选择映射法[8],并且结合加载负荷确定各面的网格密度,使计算精度达到满意效果。
3.2 加载与求解
为减少计算量,将热流密度等效为丝杠有效行程上的热流密度,均匀地添加在丝杠表面,并将轴承和电机的热载荷分别加载在模型上,最后根据表3设置换热系数,进行温度场求解。以20℃作为环境温度,n=1500r/min,可得温度场分布云图,如图1所示。
由图1可知,当丝杠转速为1500r/min时,丝杠温度约为34.6℃,电机温度约为42.4℃,轴承温升较低,前轴承温度约为28.4℃,后轴承温度约为30.5℃。
改变滚珠丝杠的转速,分析初始温度为20℃,丝杠转速为500r/min和1000r/min时系统的温度场分布情况,得到不同转速下滚珠丝杠副的温度场分布云图,如2所示。

图1 1500r/min温度场分布云图Fig.1 the map of tire temperature field at 1500 r/min
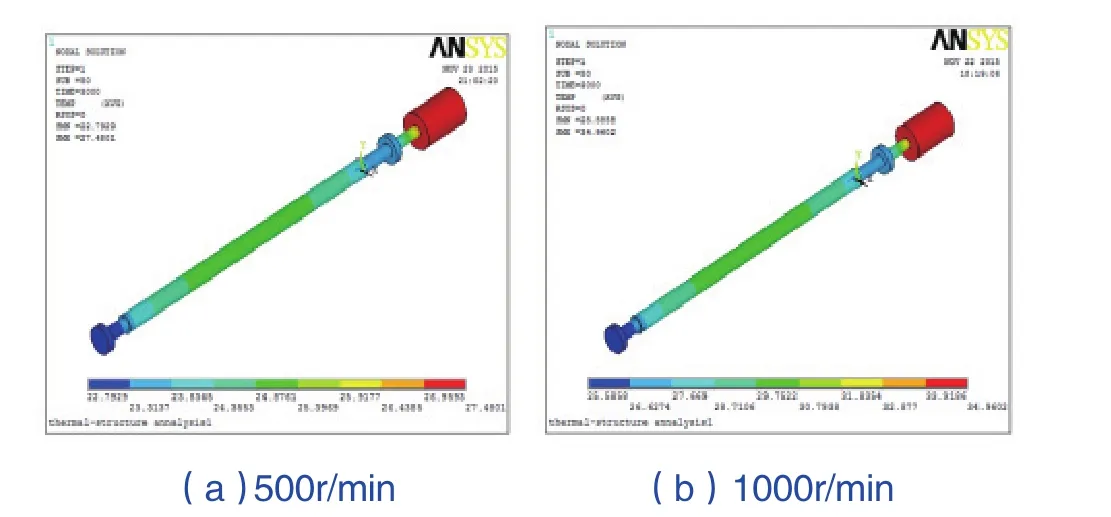
图2 温度场分布云图Fig.2 the map of tire temperature field
综合分析图1、图2可知,滚珠丝杠副在工作过程中温度最高的是电机,其次是丝杠,前后轴承的温度相对较低,后轴承的温度略高于前轴承的温度,这是由于后轴承距离电机较近,电机发热产生的热量传导到轴承上,使温度略高于前轴承,且丝杠靠近电机一端的温度明显高于远离电机一端。可想而知,电机发热对滚珠丝杠副的热变形有重要影响,不可忽略。
初始温度为20℃,分别在前后轴承、丝杠和电机上取节点,测量不同的丝杠转速下各个节点的温度值,其结果如表4所示。
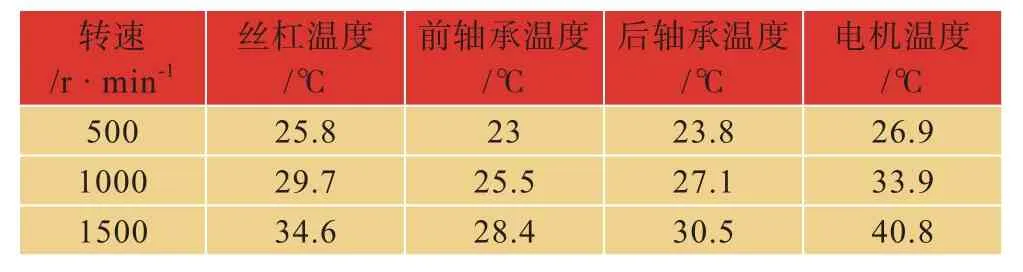
表4 模型仿真温度测试结果Tab.4 Model simulation temperature test results
根据仿真结果做出丝杠转速与各零件温升的关系图,如图3所示,由图可知,总体来看滚珠丝杠副系统各部分的温升与转速成正比。
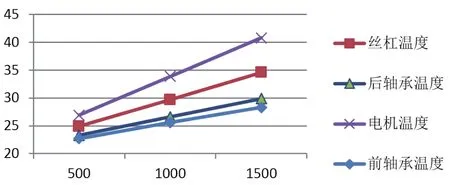
图3 各部分温度与转速关系图Fig.3 the diagram of each parts’ temperature and rotational speed
3.3 温度场实验验证
实验选择北京机床所的高速精密滚珠丝杠副寿命试验台。它能完成包括寿命、温升、噪声、预紧力矩等的精确测量。
测量温升时,采用PT100吸附式高精度温度传感器,其底部有磁铁可以直接吸附在滚珠丝杠副螺母法兰盘上。初始温度为20℃,保证环境温度不变,被测滚珠丝杠副各种转速下的测量温度,如表5所示。
对比表4、表5的结果可以看出,实验结果和仿真结果有一定的偏差,这些偏差与仿真时参数的选择与计算以及实验时的环境条件有关,偏差在允许范围内,所以温度场仿真分析的结果用于热变形的仿真分析是可行的。同时测出丝杠的长度的最终伸长量为0.22mm。
改变初始温度,其他条件不变,分别得出当初始温度为5℃(冬天)和30℃(夏天)、转速为1000r/min时,滚珠丝杠的温度场分布云图,如图4所示。

图4 1000r/min温度场分布云图Fig.4 the map of tire temperature field at 1500 r/min
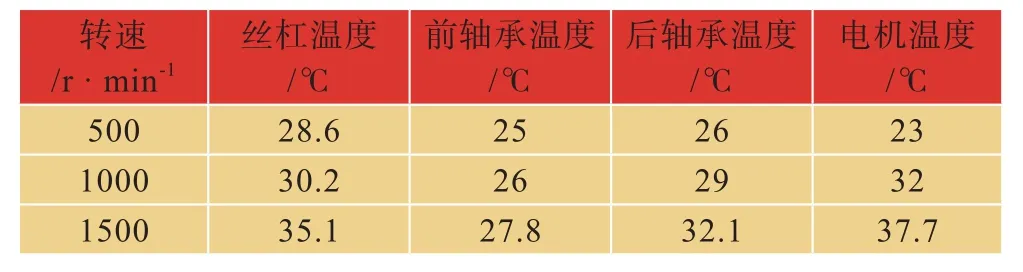
表5 实验温度测试结果Tab.5 Experimental results of temperature test
根据图2、4得出不同初始温度,转速为1000r/min时滚珠丝杠副的温升情况,结果如表6所示。从表可以看出,当环境温度变化时,滚珠丝杠副的各零件的温升值相差不大。
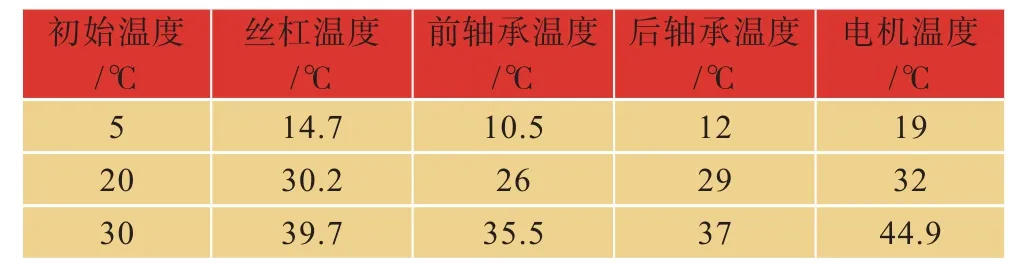
表6 不同初始温度下温升结果Tab.6 the results of temperature rise at different initial temperatures
4 滚珠丝杠副热变形仿真分析
热变形分析是在温度场分析的基础上进行的,是将温度场作为结构分析的载荷添加到模型上[9],进行计算仿真。本文主要分析单边固定条件下,丝杠的轴向变形情况。
运用ANSYS软件分析得出,当丝杠转速为1500r/min时,系统的热变形云图和应力分布云图如图5所示。
截取丝杠部分的应力和位移的分布云图,如图6示。从图6(a)可知丝杠轴向的最大位移量在前轴承,远离电机和约束一端,最大位移量是0.186mm,由图6(b)丝杠的热应力分布图可以看出,热应力在丝杠的两端较大,中间部分应力较小。
改变丝杠的转速,根据转速为1500r/min的滚珠丝杠副热变形分析的方法,仿真分析转速为1000r/min时,相同的约束方式下,整体的热变形和热应力的分布云图如图7所示。
综合以上分析可知,滚珠丝杠副在一端固定,一端自由的安装方式下,由于自身摩擦力矩和电机发热等的影响,会产生热变形,热变形量主要在自由端,且转速越大,变形量越大,应力主要集中在丝杠的两端,丝杠的中间部分应力相对较小。转速为1500r/min时,丝杠轴向的最大伸长量为0.197mm,与实验测得的0.22mm相比较有一定的误差。分析误差产生原因,一方面是温度场分析产生的误差,另一方面是实验环境和测量误差引起的。
利用ANSYS分析初始温度分别为5℃和30℃,转速为1000r/min时滚珠丝杠的热变形情况,得出最大变形量及热应力值如表7所示。
由表7可知,相同的转速和载荷下,初始温度越高,热变形量越大,但热应力没有变化。因此环境温度对于滚珠丝杠的热特性也有一定影响。

图5 1500r/min整体分布云图Fig.5 the whole distribution map at 1500r/min
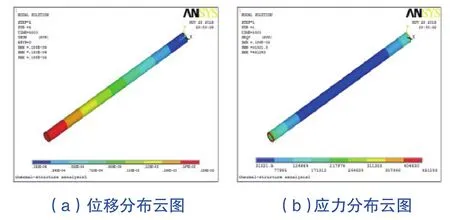
图6 丝杠分布云图Fig.6 Screw distribution map

图7 1000/min整体分布云图Fig.7 the whole distribution map at 1000r/min
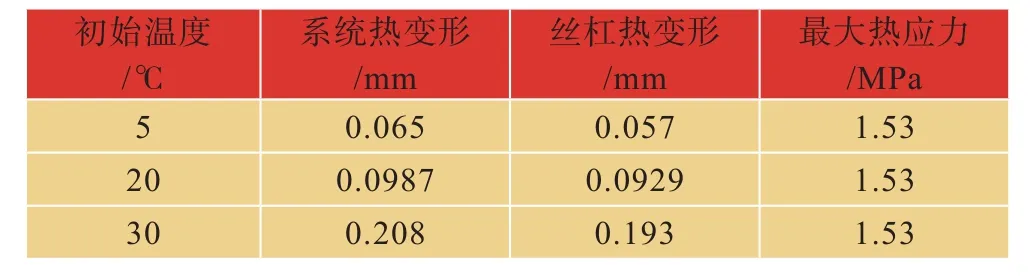
表7 不同环境温度下的热变形Tab.7 Thermal deformation under different ambient temperature
5 结语
本文首先计算了各热源的发热量以及边界对流条件,进而建立三维模型,运用ANSYS对滚珠丝杠副进行温度场和热变形分析,得出了不同速度和不同初始温度情况下系统的温度场分布云图及热变形云图,并通过实验验证了分析的正确性。
从分析中得出滚珠丝杠系统中电机的温升最高,丝杠次之,与电机相连的丝杠端的温升略高于另一端,从而证明电机发热对丝杠有重要影响,并得出滚珠丝杠的温升和转速成正比的结论。进而对一端固定一端自由安装方式下的滚珠丝杠进行了热变形分析,并分析了不同转速下的热变形情况,发现丝杠自由端的热变形量最大,热应力主要集中在丝杠两端,中间部分的热应力分布较均匀且应力较小。随着初始温度的升高,热变形量逐渐增大,证明环境温度对滚珠丝杠副的热特性也有重要影响,进而可通过控制环境温度来减小热变形。本文的研究为优化滚珠丝杠副提供了理论支持,为改善滚珠丝杠副,实现高速化发展做出贡献。
[1] 陈婉,王科社,宋杰,等. 高精度滚珠丝杠最佳接触角的分析与验证[J]. 新型工业化,2016,6(9):53-57. CHEN Wan,Wang Ke-she,Song Jie,et al. Analysis and Verification of the Best Contact Angle in Ball Screw [J]. The Journal of New Industrialization,2016.6 (9):53-57.
[2] 浦广益. ANSYS Workbench基础教程与实例详解[M]. 北京:中国水利水电出版社,2013:48-52. PU Guang-yi. ANSYS Workbench basic tutorial and example explanation[M]. Beijing:Chinese Water Conservancy and Hydropower Press,2013:48-52.
[3] Wei C C,Lai R S. Kinematical analyses and transmission efficiency of a preloaded ball screw operating at high rotational speeds[J]. Mechanism and Machine Theory,2011,46(7):880-898.
[4] 缪亚雄. 滚珠丝杠系统的热特性建模与分析研究[J]. 中国制造业信息化,2008,37(3):46-48. MIU Ya-xiong. Modeling and analysis of thermal characteristics of ball screw system [J]. China manufacturing information,2008,37 (3):46-48.
[5] 王文竹. 滚珠丝杠副的接触变形及其传动系统的温度场分析[D]. 沈阳:东北大学,2010. WANG Wen-zhu. Contact deformation of ball screw pair and analysis of temperature field of transmission system [D]. Shenyang:Northeastern University,2010.
[6] T. A. Harris,M. N. Kotzalas. 滚动轴承分析[D]. 机械工业出版社,2010. T. A. Harris,M. N. Kotzalas. Analysis of rolling bearing [D]. Machinery Industry Press,2010.
[7] Jui P H,Wu J S,Chiu J Y. Impact failure analysis of re-circulating mechanism in ball screw[J]. Engineering Failure Analysis,2004,11:561-573.
[8] 周忆,张恒,刘芳.平板型水润滑橡胶轴承摩擦噪声的有限元分析[J]. 新型工业化,2013,3(10):67-72. ZHOU Yi,ZHANG Heng,LIU Fang. Finite Element Analysis of Friction Noise of Plate Type Water Lubricated Rubber Bearings [J]. The Journal of New Industrialization,2013,3(10):67-72.
[9] 陈祯. 高速滚珠丝杠进给系统动态性能检测与热特性研究[D]. 兰州:兰州理工大学,2012. CHEN Zhen. Study on detection of thermal characteristics and dynamic performance of high speed ball screw feed system [D]. Lanzhou:Lanzhou University of Technology,2012.
Thermal Analysis of High Performance Ball Screw Pair by Finite Element Method
CHEN Wan, WANG Ke-she, SONG Jie, DONG Qing-xia
Beijing Information Science & Technology University, Beijing, 100192
Based on the relevant knowledge of heat transfer, calculate the screw of, bearing and motor three heat source of ball screw’s heat and convection coefficient of boundary. By using finite element analysis software, temperature field simulation analysis was carried out on the ball screw pair, found out that temperature approximation is proportional to the speed and the highest temperature is the motor. Then make an experimental verification for the parts temperature condition to prove the correctness of the simulation results. On this basis, the thermal deformation analysis was carried out on the ball screw pair. It is concluded that the thermal deformation and thermal stress distribution nephogram. Analyze the influence of the rotational speed and initial temperature on the thermal deformation. Results show that the greater the speed, the higher the initial temperature, and the bigger the thermal deformation. In addition, the thermal stress is mainly concentrated on both ends of screw, while the middle part of the thermal stress distribution is evener and less stress.
Ball screw; Temperature field; Thermal deformation; Finite element analysis
陈婉,王科社,宋杰,等.高性能滚珠丝杠副有限元热分析[J]. 新型工业化,2016,6(11):58-63.
10.19335/j.cnki.2095-6649.2016.11.007
: CHEN Wan, WANG Ke-she, SONG Jie, et al. Thermal Analysis of High Performance Ball Screw Pair by Finite Element Method[J]. The Journal of New Industrialization, 2016, 6(11) : 58-63.
北京市科技计划课题(121100001612010)
陈婉(1991-),女,硕士研究生,主要从事滚珠丝杠性能研究
王科社(1958-),男,硕士生导师,研究方向为机械设计、可靠性理论。

