水力效应对裂缝边坡稳定性影响的上限分析
邹 飞, 程 肖, 赵炼恒, 李 亮
(1.贵州省交通规划勘察设计研究院股份有限公司, 贵阳 550081;2.中南大学土木工程学院, 长沙 410075;3.贵州省交通建设工程质量监督局, 贵阳 550000)
水力效应对裂缝边坡稳定性影响的上限分析
邹 飞1,2,3, 程 肖2, 赵炼恒2, 李 亮2
(1.贵州省交通规划勘察设计研究院股份有限公司, 贵阳 550081;2.中南大学土木工程学院, 长沙 410075;3.贵州省交通建设工程质量监督局, 贵阳 550000)
为了解决地下水位变化对裂缝边坡稳定性的影响,基于极限分析上限法及强度折减技术,将孔隙水压力以外力的形式参与能耗计算,分析了水力效应对裂缝边坡稳定性影响,重点研究了临界裂缝深度和最不利裂缝位置随地下水位、边坡坡角的变化规律. 研究结果表明:地下水位、边坡坡角对最不利裂缝位置及临界裂缝深度的影响显著;当地下水位较低时,最不利裂缝随地下水位的增大逐渐靠近坡顶缘;在裂缝位置已知及裂缝深度、位置均未知的情况下,临界裂缝深度受地下水位的影响呈现出不同的规律性. 所得成果为研究复杂条件下的边坡坡顶临界裂缝深度及最不利裂缝位置提供了一种新思路.
孔隙水压力;裂缝边坡;极限分析上限法;最不利裂缝位置;临界裂缝深度
大量工程实践发现多数边坡表面存在大量的裂缝,裂缝产生的原因有多种,如土的干湿循环、土的胀缩性、极端天气条件、泥化夹层及地震作用等. 裂缝的存在为地下水、降雨等渗入边坡内部提供了便利通道,尤其当裂缝充满水时,会加大边坡的下滑力,进而加速坡体失稳破坏过程. 俗话说“十个边坡九个水”,可见水压力是影响边坡稳定性的重要客观因素,尤其对含有裂缝的边坡. 因此,研究地下水位升降对裂缝边坡稳定性影响具有重大的理论意义. 赵炼恒等[1-2]采用极限平衡法和极限分析上限法研究了河流水位升降和流水淘蚀以及地下水位变化对边坡稳定性影响;王均星等[3-4]、Kim等[5]、殷建华等[6]基于极限分析上下限有限元理论,探讨了孔隙水压力对土坡稳定性影响;Utili[7]采用极限分析上限法,在裂缝水不下渗至裂缝下部土体的假设下,分析了裂缝水压力对边坡稳定性的影响;Viratjandr等[8]采用直线型及对数螺旋线破坏面,基于极限分析上限法分析了临河边坡稳定性,并给出了一系列计算图表,但文中未考虑裂缝的存在;Michalowski[9-11]通过引入孔隙水压力系数近似计算破坏面上的孔隙水压力,将其作为外力参与能耗计算;邓东平等[12-14]基于极限平衡理论考虑张裂缝的存在,假设滑动面为直线型、圆弧型或任意曲线,对水力条件下临河边坡稳定性和渗流条件下的边坡稳定性进行了相关研究;蒋斌松等[15]根据极限平衡原理,给出了静水压力作用下裂缝边坡平面滑动面的最小安全系数解析计算式. 以上研究推进了水力效应下边坡稳定性研究的进展,然而还存在以下不足:1)多数研究以平面破坏面为破坏模式,采用旋转破坏机制进行研究的相关报道较为少见;2)一般先假定裂缝的深度再进行下一步分析计算,不能确定用于计算的裂缝对边坡稳定性影响最大.
本文基于前人的研究成果,采用极限分析上限法以对数螺旋线旋转机构为破坏模式,结合强度折减技术给出孔隙水压力作用下裂缝边坡安全系数解析式,并通过对比分析,验证本文方法的有效性. 进一步研究地下水位、裂缝深度或裂缝位置及边坡坡角对裂缝边坡稳定性的影响,重点寻求水力效应下,临界裂缝深度及最不利裂缝位置的变化规律.
1 考虑孔隙水压力的裂缝边坡稳定性分析
总结目前孔隙水压力对土质边坡稳定性影响分析方法,可分为以下两大类:1) 针对渗流作用,将流网和浸润线进行合理简化,求出各点的孔隙水压力[3-4,12-14];2) 将孔隙水压力以外力的形式作用在滑裂面上[1-2,8-11,16]. 根据流网计算水力效应时,一般地下水位上、下的岩土参数取值不同. 然而,基于极限分析上限法,将孔隙水压力作为外力参与能耗计算时,假定土体强度不受水位升降的影响,因而在计算过程中土重采用天然容重[8-11]. Viratjandr等[8]讨论了4种水位变化情况(突降、渐降、缓降、稳降),给出了临河边坡孔隙水压力做功计算公式
(1)
式中:γw为水的容重;ω为滑动土体绕旋转中心旋转的角加速度;r0为对数螺旋线θ=θ0时的极径;f5为与地下水位做功有关的函数,具体情况详见文献[8].
本文采用文献[8]中孔隙水压力计算方法,对真实水力梯度分布进行简化,假定等势线铅直,该假设使计算结果偏于保守,设计偏于安全.
1.1 边坡的几何要素及计算模型
假定裂缝位于坡顶(图1中的EF面),取过坡趾下方的对数螺旋线破坏模式进行分析,见图1. 其中图1(a)为裂缝含有水时的破坏模式图,图1(b)为裂缝无水时的破坏模式图. 图中W为滑动土体的重力,Fw为裂缝水集中作用力,Fp为孔隙水压力,z1、z2、z3是3个区域坡体水位至滑动面的垂直距离. 边坡的几何要素如下:边坡高度H,坡面倾角β,裂缝深度δ,裂缝中水位高度δw,地下水位距坡脚的垂直距离h,裂缝距坡顶缘E的水平距离l,E点距F点的水平距离L1,裂缝距F点的水平距离L2,破坏机制角度参数θ0、θh及β′,表征地下水位的角度参数θ1~θ3,与裂缝有关的角度θc,点P为旋转中心,ω为滑动土体绕旋转中心旋转的角加速度,r0、rh为对数螺旋线的极径.
因为本文假设破坏面过裂缝最底端,所以裂缝深度δ和位置l并不是相互独立的参数,下面将从以下3个方面说明裂缝深度δ和位置l的几何关系.
1) 给定裂缝深度
裂缝深度已知时,θc可由未知量θ0、θh表示,进而,裂缝位置l为未知量θ0、β′、θh的函数.
(2)
基于Matlab软件,通过搜索最危险滑动面获得该条件下的裂缝位置,即最不利裂缝位置.
2) 给定裂缝位置
裂缝位置已知与裂缝深度已知类似,θc可由未知量θ0、θh表示,裂缝深度δ为未知量θ0、θh的函数.
(3)
基于Matlab软件,通过搜索最危险滑动面获得该条件下的裂缝深度,即临界裂缝深度.
3) 裂缝深度和位置均未给定
对于该情况,裂缝深度δ及裂缝位置l计算表达式同式(2)(3),但式中θc是未知的,δ和l是θ0、β′、θh、θc的函数. 基于Matlab软件,通过搜索最危险滑动面获得该条件下的裂缝深度和位置,即临界裂缝深度及最不利裂缝位置.
1.2 安全系数公式推导
本文基于强度折减技术以安全系数指标来评价孔隙水压力对边坡稳定性的影响,通过求解安全系数最小值来获取最不利裂缝位置或临界裂缝深度. 外功率包括滑动土重所做功率Wr、孔隙水压力所做功率Wu及裂缝中水压力所做功率Ww. 根据虚功原理,使内功率Wd等于外功率,即可求得目标函数解析式.
Ww+Wu+Wr=Wd
(4)
对于土体重力做功和内部能耗计算方法在文献[7]中已详细介绍,为节省篇幅,本文不再赘述. 重点介绍裂缝边坡孔隙水压力做功表达式的计算方法.
1.2.1 外力做功
1.2.1.1 重力做功
重力做功由PFD′区土重做的功率减去PEF、PED′、EDD′和BCF区土重做的功率,BCF区土重做的功率等于PFC区土重做的功率减去PFB、PBC区土重做的功率.
(5)
式中:γ为土体容重;f1~f4,p1~p3是与θ0、θc、θh、β、β′及φ相关的函数,具体表达式见文献[7].
1.2.1.2 孔隙水压力做功
孔隙水压力做功采用积分方法计算. 裂缝中有没有水压力做功以及孔隙水压力积分范围均与地下水位的位置有关. 下面以地下水位位于裂缝最底端为分界点,分别讨论0≤H-h≤δ和H-h>δ时,裂缝中水压力和孔隙水压力做功情况.
由几何关系易得坡体水位至滑动面的垂直距离z1、z2、z3(如图1所示)的表达式为
(6)
角度参数θ1、θ2、θ3的表达式为
(7)
1) 0≤H-h≤δ
当0≤H-h≤δ时,地下水位高于裂缝最底端,需考虑裂缝水压力做功,孔隙水压力从角度θc开始积分,见图1(a).
① 裂缝中水压力做功
裂缝中水压力做功采用集中力的形式,计算结果为
(8)
其中
(9)
② 孔隙水压力做功
孔隙水压力做功采用文献[8]的计算方法
(10)
式中:f1是与θc至θ2区域内孔隙水压力做功有关的积分表达式;f2是与θ2至θ3区域内孔隙水压力做功有关的积分表达式;f3是与θ3至θh区域内孔隙水压力做功有关的积分表达式.
(11)
(12)
(13)
f1~f3具体计算结果见附录.
2)H-h>δ
当H-h>δ时,地下水位低于裂缝最低端,裂缝中无水压力作用即Ww=0,此时,孔隙水压力做功从θ1开始积分,见图1(b). 孔隙水压力计算公式同式(8),但f1变为与θ1至θ2区域内孔隙水压力做功有关的积分表达式f1*;f2与f3不变,同式(12)和式(13).
(14)
f1*具体计算结果见附录.
1.2.2 内部能耗
对于能量分析法,内部能耗只考虑间断面CD′上土体间的能量耗散,当破坏面过坡趾时D′与D重合. 内部能量耗损率为
(15)
1.2.3 边坡安全系数
根据能耗法计算过程,令外荷载所做的功率等于内部耗损率,将c、φ进行强度折减,经折减后的强度指标算式变为
(16)
根据能耗法计算过程,令外荷载所做的功率等于内部耗损率,可求得边坡安全系数
(17)
式中:f1~f4、p1~p3、f1~f3意义同前;fw中的内摩擦角φ均由φf代替.
式(17)即为基于极限分析上限法,考虑孔隙水压力作用下的裂缝边坡安全系数计算公式. 将Fs作为目标函数,通过序列二次规划法,搜索安全系数最小值,来获取该情况下的临界破坏面及此时的最危险裂缝. 具体程序实现过程可参考文献[17].
2 计算对比与分析
2.1 对比分析
本文所采用方法的基本原理与文献[8]相同,但文献[8]中的无裂缝边坡为本文研究对象的特例,故令本文裂缝深度δ=0 m,计算结果应与其坡外水位为0 m的情况完全一致. 采用文献[8]图10中的算例,见图2.
由于从文献[8]图形上读取数据时难免会出现误差,本文计算结果与文献[8]略有差异,但最大误差不超过1%(0.82%),对比可以表明本文推导与优化计算的正确性.
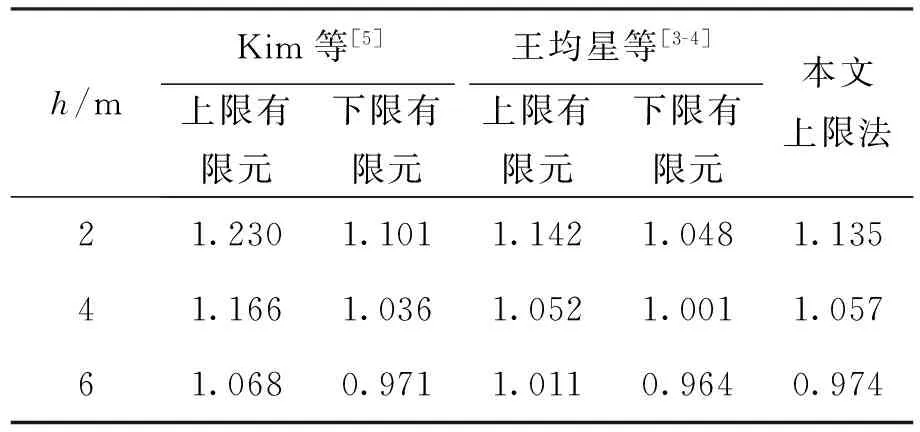
针对本文裂缝已知的情况,取边坡高度H=10 m,坡角β=45°,土层参数γ=18 kN/m3,c=20 kPa,φ=15°,令裂缝深度δ=0 m,计算地下水位h=2、4、6 m时的安全系数值,与已有研究成果对比情况见表1.
表1 边坡安全系数对比分析
Table 1 Comparisons of safety factor between the present results and the approach solutions in existence
h/mKim等[5]王均星等[3-4]上限有限元下限有限元上限有限元下限有限元本文上限法21.2301.1011.1421.0481.13541.1661.0361.0521.0011.05761.0680.9711.0110.9640.974
由表1可知,本文研究结果与已有结果非常接近.
鉴于目前采用极限分析上限法及对数螺旋线破坏面分析水力效应对裂缝最不利位置及裂缝临界深度影响的研究甚少,本文取2组算例同时进行计算,便于对比验证. 采取的具体算例如下:
算例1:边坡高度H=10 m,坡度1∶2,土重γ=20 kN/m3,黏聚力c=10 kPa,内摩擦角φ=20°,水位高度h=3 m. 裂缝深度已知时取δ/H=0.2,裂缝位置已知时取l=1 m.
算例2:边坡高度H=10 m,坡角β=45°,土重γ=17.86 kN/m3,黏聚力c=32 kPa,内摩擦角φ=30°,水位高度h=7 m. 裂缝深度已知时取δ/H=0.2,裂缝位置已知时取l=2.5 m.
2.2 已知裂缝深度,裂缝最不利位置研究
已知裂缝深度,研究地下水位h、裂缝深度δ及坡角β对最不利裂缝位置的影响规律. 研究某个参数对最不利裂缝位置的影响时,其他参数的取值见算例1与算例2. 图3中Fs-1、Fs-2分别指算例1、算例2的安全系数Fs曲线,l-1、l-2分别指算例1、算例2的最不利裂缝位置l曲线(l是裂缝距坡顶缘E的水平距离). 下面详细分析不同参数对边坡稳定性及最不利裂缝位置的影响规律.
地下水作为影响边坡稳定的不利因素,与预想结果一致,地下水位越高边坡越不稳定. 随着地下水位由0变化到0.9H,最不利裂缝位置l随地下水位的增大先减小后增大,见图3(a). 当地下水位h/H>0.8时,裂缝中含有水,最不利裂缝位置变化更加显著.
安全系数或最不利裂缝位置随裂缝深度的变化曲线见图3(b). Utili[7]的研究结果表明:当β<90°时,随着裂缝深度的增大,稳定系数先减小后增大,β越小,曲线变化点对应的裂缝深度越小. 由于算例2的坡角较算例1大,因此,当裂缝深度在0~0.3H变化时,图3(b)中Fs- 1曲线随着裂缝深度的增大先减小后增大,Fs- 2曲线随着裂缝深度的增大逐渐减小. 作者已验证,裂缝深度从0变化到0.55H,Fs- 2曲线也会呈现先减小后增大的变化趋势. 裂缝深度从0变化到0.3H,最不利裂缝距坡顶缘的距离不断减小.
安全系数或最不利裂缝位置随边坡坡角的变化曲线见图3(c). 边坡越陡,安全系数越小,边坡越不稳定. 随着坡角的增大,最不利裂缝位置逐渐远离坡顶缘.
以上分析可知,随着地下水位、裂缝深度及坡角的变化,算例1和算例2所得的安全系数曲线及裂缝最不利位置曲线变化趋势基本相同.
2.3 已知裂缝位置,裂缝临界深度变化规律研究
已知裂缝位置,研究地下水位h、裂缝距坡顶缘的距离l、坡角β对临界裂缝深度的影响规律. 研究某个参数对临界裂缝深度的影响时,其他参数的取值见算例1与算例2. 图4中Fs- 1、Fs- 2曲线代表的意义同图3,δ/H-1、δ/H-2分别指算例1和算例2的临界裂缝深度曲线.
安全系数或临界裂缝深度随地下水位的变化曲线见图4(a). 随地下水位由0变化到0.9H,安全系数不断减小,临界裂缝深度先增大,但当临界裂缝深度增大到(H-h),将线性减小且始终保持δ=H-h.
安全系数或临界裂缝深度随裂缝位置的变化曲线见图4(b). 当给定裂缝位置时,因为算例1与算例2的安全系数及临界裂缝深度相差较大,所以计算结果不宜展示在同一图中. 算例1及算例2的安全系数及临界裂缝深度变化曲线分别见图4(b-1)及4(b-2). 裂缝距坡顶缘的距离由1 m变化至4 m,安全系数先减小后增大,算例1的临界裂缝深度先增大后减小,而算例2的临界深度先保持不变为δ=H-h=3 m,当裂缝距坡顶缘的距离增大到一定值后,随其增大临界裂缝深度大致呈线性减小. 为了探讨地下水位对临界裂缝深度随裂缝位置变化规律的影响,图4(b-3)给出了算例1地下水位h=8 m对应的临界裂缝深度变化曲线,随着裂缝远离坡顶缘,临界裂缝深度变化规律同算例2. 可见地下水位是影响临界裂缝深度变化的重要因素之一. 图4(b-4)给出了β=26.565°、h=3 m对应的算例2临界裂缝深度变化曲线,其变化规律同算例1. 可见坡角也是影响临界裂缝深度变化规律不可忽略的因素. 以上分析可知,地下水位及坡角对临界裂缝深度随裂缝位置的变化规律影响较大,当地下水位较高,裂缝距坡顶缘较近时,临界裂缝深度将不随裂缝位置的变化而变化;当裂缝距坡顶缘较远时,临界裂缝深度随裂缝位置l的增大而减小.
安全系数或临界裂缝深度随坡角的变化曲线见图4(c-1). 边坡安全系数随坡角的增大不断减小. 算例1的临界裂缝深度随坡角的增大不断增大;当β<45°时,算例2的裂缝临界深度随坡角的增大逐渐增大,当β≥45°时,裂缝临界深度恒等于地下水位距坡顶的垂直距离H-h. 为了探讨地下水位对临界裂缝深度随坡角变化规律的影响,图4(c-2)给出了地下水位h=7 m对应的算例1及h=8 m对应的算例2临界裂缝深度变化曲线. 当地下水位低于某个值x1时,临界裂缝深度随裂缝距坡顶缘距离的增大而增大;当地下水位高于某个值x2
时,临界裂缝深度将不受坡角的影响;当地下水位x1≤h≤x2时,临界裂缝深度随裂缝距坡顶缘距离的增大先增大后恒等于H-h. 上述研究表明在孔隙水压力作用下,当坡角较大,地下水位较高时,临界裂缝深度将不受坡角变化的影响.
以上分析可知,地下水位和坡角是导致算例1和算例2临界裂缝深度变化趋势存在差异的重要原因. 地下水位较高时,临界裂缝深度将不受裂缝位置及较大坡角的影响.
2.4 裂缝深度和位置均未给定
裂缝深度和位置均未知的情况下,探讨地下水位h、坡角β对裂缝临界深度和最不利位置的影响. 研究某个参数对裂缝临界深度的影响时,其他参数的取值见算例1与算例2.
图5是地下水位为2、3、4 m对应的破坏模式图. 破坏模式图可以较为直观地展现临界裂缝深度、最不利位置及临界破坏面. 随地下水位的升高,临界裂缝深度逐渐增大,最不利裂缝逐渐靠近坡顶缘.
图6是坡角为30°、45°、60°对应的的破坏模式图. 随坡角的增大,临界裂缝深度逐渐增大,最不利裂缝位置逐渐靠近坡顶缘.
3 结论
本文在特定边坡条件下初步研究了地下水位及坡角对最不利裂缝位置与临界裂缝深度的影响. 总结以上研究可得如下结论:
1) 边坡安全系数随地下水位及坡角的增大而减小.
2) 当裂缝深度已知时,最不利裂缝随地下水位的升高先靠近坡顶缘后又远离,随裂缝深度的增大而靠近坡顶缘,但随坡角的增大逐渐远离坡顶缘.
3) 当裂缝位置已知时,随着地下水位的升高,临界裂缝深度不断增大,但当临界裂缝深度增大到H-h时,将以δ=H-h的关系式线性减小;地下水位较高时,临界裂缝深度将不受裂缝位置及较大坡角的影响.
与其他研究方法类似,本文对计算模型进行了合理简化,研究成果对后续工作的开展有一定参考价值. 同时裂缝前侧土体滑动对后侧土体稳定性影响值得深入研究.
讨论1:在孔隙水效应下,边坡临界破坏面可能从裂缝中间(图1中B点与C点之间)某部位穿过,土体也可能从点C以下某部位开始滑动. 本文仅就边坡临界破坏面恰好通过裂缝最底端(C点)进行了讨论,其他两种情况下的边坡稳定性及临界裂缝变化规律还需进一步深入研究.
讨论2:本文主要采用极限分析上限法分析孔隙水对裂缝边坡稳定性及裂缝最不利位置和临界深度的影响. 同时鉴于极限分析上限法无法获知有关滑体位移的相关信息,本文目前假设裂缝后侧及破坏面下部土体保持静止,仅考虑BEDD′CB区域的土重做功及发生在CD′(D)面上的内能耗散. 在后续研究工作中,将对裂缝后侧土体的稳定情况深入探讨.
附录
f1=[e3tan φ(θ2-θ0)(3tanφsinθ2-cosθ2)+
e3tan φ(θc-θ0)(cosθc-3tanφsinθc)]/(1+9tan2φ)-
(1)
f2=[(3tanφsinθ3-cosθ3)e3(θ3-θ0)tan φ+
e3(θ2-θ0)tan φ(cosθ2-3tanφsinθ2)]/(1+9tan2φ)-
tanβ[(3tanφcosθ3+sinθ3)e3(θ3-θ0)tan φ-
e3(θ2-θ0)tan φ(sinθ2+3tanφcosθ2)]/(1+9tan2φ)-
(2)
f3=[(3tanφsinθh-cosθh)e3(θh-θ0)tan φ+
e3(θ3-θ0)tan φ(cosθ3-3tanφsinθ3)]/(1+9tan2φ)-
(3)
f1*=[(3tanφsinθ2-cosθ2)e3(θ2-θ0)tan φ+
e3(θ1-θ0)tan φ(cosθ1-3tanφsinθ1)]/(1+9tan2φ)-
(4)
[1] 赵炼恒, 罗强, 李亮, 等. 水位升降和流水淘蚀对临河路基边坡稳定性的影响[J]. 公路交通科技, 2010, 27(6): 1-8. ZHAO L H, LUO Q, LI L, et al. Study on stability of subgrade slope along river subjected to water level fluctuation and stream erosion[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 1-8. (in Chinese)
[2] 赵炼恒, 罗强, 李亮, 等. 地下水位变化对边坡稳定性影响的上限分析[J]. 公路交通科技, 2010, 27(7): 1-7. ZHAO L H, LUO Q, LI L, et al. Analysis of upper bound of slope stability considering ground water level fluctuations[J]. Journal of Highway and Transportation Research and Development, 2010, 27(7): 1-7. (in Chinese)
[3] 王均星, 李泽, 陈炜. 考虑孔隙水压力的土坡稳定性的有限元下限分析[J]. 岩土力学, 2005, 26(8): 1258-1262. WANG J X, LI Z, CHEN W. Lower bound analysis of soil slope stability using finite elements subjected to pore water pressure[J]. Rock and Soil Mechanics, 2005, 26(8): 1258-1262. (in Chinese)
[4] 王均星, 李泽. 考虑孔隙水压力的土坡稳定性的有限元上限分析[J]. 岩土力学, 2007, 28(2): 213-218. WANG J X, LI Z. Upper bound analysis of stability of soil slope subjected to pore water pressure using finite elements [J]. Rock and Soil Mechanics, 2007, 28(2): 213-218. (in Chinese)
[5] KIM J M, SALGADO R, YU H S. Limit analysis of soil slope subjected to Pore-water Pressures [J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(1): 49-58.
[6] 殷建华, 陈健, 李焯芬. 考虑孔隙水压力的土坡稳定性的刚体有限元上限分析[J]. 岩土工程学报, 2003, 25(3): 273-277. YIN J H, CHEN J, LI C F. A rigid finite element method for upper bound limit analysis of soil slopes subjected to pore water pressure [J]. Chinese Journal of Geotechnical Engineering, 2003, 25(3): 273-277. (in Chinese)
[7] UTILI S. Investigation by limit analysis on the stability of slopes with cracks[J]. Geotechnique, 2013, 63(2): 1-15.
[8] VIRATJANDR C, MICHALOWSKI R L. Limit analysis of submerged slopes subjected to water drawdown[J]. Canadian Geotechnical Journal, 2006, 43(8): 802-814.
[9] MICHALOWSKI R L. Stability assessment of slopes with cracks using limit analysis[J]. Canadian Geotechnical Journal, 2013, 50(10): 1011-1021.
[10] MICHALOWSKI R L. Slope stability analysis: a kinematical approach[J]. Geotechnique, 1995, 128(4): 283-293.
[11] MICHALOWSKI R L. Stability charts for uniform slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 123(6): 351-355.
[12] 邓东平, 李亮. 渗流条件下具有张裂缝边坡的稳定性分析[J]. 中南大学学报 (自然科学版), 2013, 44(1): 294-302. DENG D P, LI L. Stability analysis of slope with tensile crack under condition of seepage[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 294-302. (in Chinese)
[13] 邓东平, 李亮, 赵炼恒. 河岸边坡稳定性及张裂缝最不利位置研究[J]. 中南大学学报 (自然科学版), 2013, 44(9): 3873-3883. DENG D P, LI L, ZHAO L H. Critical position of tensile cracks and stability analysis in slope near river[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3873-3883. (in Chinese)
[14] 邓东平, 李亮, 赵炼恒. 稳定渗流条件下土坡稳定性分析的一种新方法[J]. 工程地质学报, 2011, 19(1): 29-36. DENG D P, LI L, ZHAO L H. A new method of stability analysis of earth slope under the condition of steady seepage[J]. Journal of Engineering Geology, 2011, 19(1): 29-36. (in Chinese)
[15] 蒋斌松, 蔡美峰, 都浩. 平面滑动边坡稳定性的解析计算[J]. 岩石力学与工程学报, 2004, 23(1): 91-94. JIANG B S, CAI M F, DU H. Analytical calculation on stability of slope with planar failure surface[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(1): 91-94. (in Chinese)
[16] BISHOP A W. The use of pore-pressure coefficients in practice[J]. Geotechnique, 1954, 4(4): 148-152.
[17] 唐高朋, 赵炼恒, 李亮, 等. 基于MATLAB的边坡稳定性极限上限分析程序开发[J]. 岩土力学, 2013, 34(7): 2091-2098. TANG G P, ZHAO L H, LI L, et al. Program development for slope stability using MATLAB software and upper bound limit analysis[J]. Rock and Soil Mechanics, 2013, 34(7): 2091-2098. (in Chinese)
(责任编辑 郑筱梅)
Upper Bound Analysis of Cracked Slopes Subject to Hydraulic Effect
ZOU Fei1,2,3, CHENG Xiao2, ZHAO Lianheng2, LI Liang2
(1.Guizhou Transportation Planning Survey & Design Academe, Guiyang 550081, China; 2.School of Civil Engineering, Central South University, Changsha 410075, China; 3.Construction Engineering Quality Supervision Bureau of Guizhou Province, Guiyang 550000, China)
Ground water level fluctuations have greatly influence on stability of slopes with cracks. Pore-water pressure as the external force was involved in the calculation of energy consumption based on the upper bound limit analysis and strength reduction technique. The effect of pore-water pressure on stability of slopes with cracks was analysed. However, the change rules of critical depth or position of cracks under the effect of ground water level and slope angle was the focus of this paper. Results show that the critical position and depth of cracks significantly depend on the ground water level and slope angle. The increase in ground water level makes the critical crack close to slope crest in the case that ground water level is low. It is also observed that the influence of ground water level on critical depth of cracks presents different regularity for the case of crack position known and both crack position and depth unknown. Research results provide a new method for obtaining critical crack located on the upper surface of slopes under the complex condition.
pore-water pressure; slopes with cracks; upper bound limit analysis; critical position of cracks; critical depth of cracks
2016- 04- 11
国家自然科学基金资助项目(51208522, 51478477);湖南省科学技术厅科技资助项目(2012SK3231, 2012TT2039);贵州省交通运输厅科技项目(2012122033,2015122046)
邹 飞(1983—), 男, 高级工程师, 主要从事岩石动力学、边坡极限分析方面的研究工作, E-mail: zoufei05@126.com
TU 457
A
0254-0037(2016)12-1864-09
10.11936/bjutxb2016040030

