一种基于CUDA的并行SMO算法

汤斌飞, 林 超, 黄 迪

(中国石油大学(华东) a. 理学院；b. 网络及教育技术中心，山东 青岛 266580)



一种基于CUDA的并行SMO算法

汤斌飞a, 林 超b, 黄 迪a

(中国石油大学(华东) a. 理学院；b. 网络及教育技术中心，山东 青岛 266580)

序列最小优化算法(Sequential Minimal Optimization，SMO)是针对支持向量机算法执行速度慢而提出来的，它通过最小化分块来加速算法，对不同数据集来说，其算法加速可达100x～1 000x。但是随着数据量的增大，其算法执行时间仍然较慢。为了加速算法，本文结合现代较发达的图形处理单元(Graphics Processing Unit, GPU)计算，通过多处理器并行执行方式，提出对算法并行化。主要的并行点在于确定了两个参数α1、α2之后，求解局部最优，从而更新所有参数的过程是天然并行的，而且SIMD形式的并行性非常符合GPU的运算模式，通过将计算量大的参数更新部分转移到GPU进行计算，可以加速整个算法的运行。实验表明，并行算法可以达到150倍的加速效果。

SMO； CUDA； 并行SMO算法

0 引 言

SMO算法是由John C. Platt最先提出来的，其算法思想来源于Vapnik提出的“Chunking”算法[1]，通过使得分块达到最小，来加速求解二次优化问题[2]。另一方面并行计算由来已久，利用并行计算可以获得更好的性价比，更好地利用电脑的硬件设备[3]，尤其是GPU的通用计算能力。硬件平常都不会满负载工作，这在一定程度上意味着一定量的资源浪费。为使其工作更快、更好，并行计算是一个选择，其通过软件的形式，改变串行程序的计算模式，在运行正常的前提下，在同样的硬件设备上提高了计算速率。有利用MPI编程接口实现的SMO算法[4]，其算法思路为把数据集分为小份，每份单独计算完成，再进行解的合并。也有用GPU实现的SVM算法，其算法思路是在GPU端计算Kernel矩阵[5]，但这不能称为完全的并行计算[1]。

1 CUDA简介

随着GPU计算的高速发展，NVIDIA公司成功地抓住了通用计算的时代脉搏，它提出的CUDA C编程接口是基于NVIDIA架构显卡的，其通过核函数控制GPU线程进行计算，把Block运行快映射到SM以及把Thread运行单元映射到SP，通过物理结构与逻辑结构相结合的方式，成功地把SIMD架构程序转移到GPU上进行计算，通过GPU上数以千计的基本计算单元来实现中央处理单元(Centeral Processing Unit, CPU)多核所不能达到的计算效率[6-7]。近年来也有很多GPU计算接口相继问世，如可以与CUDA相比肩的AMD OpenCL编程接口[8]，也有MS提出来的可以跨平台的编程接口C++ AMP[9-10]，但是CUDA作为最基本的基于函数的编程接口，仍然受到很多编程人员的追捧。这也是因为计算本身是通过函数来体现的，是基于过程的，这也是CUDA成为常青树的一个原因。为了使计算更快、更好，GPU计算是一个很好的选择，一块显卡有时可以超过一台小型服务器的计算效率，本文也是通过在GPU平台上面实现了SMO并行算法来实现算法的加速。

2 串行SMO算法

2.1 简 介

Sequential Minimal Optimization(SMO)算法使为了解决Support Vector Machine(SVM)运行速率慢而最早提出来的，以解决二次规划问题，通过最小化“分组”，使得算法达到最快。本文仍从SVM方向来引入SMO算法，并对算法进行简单的描述[11]。

对于数据点线性可分的情况，通过最大化类间距来进行求解[12]，转化为数学公式，即为：

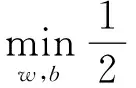
s.t.yi(wxi-b)≥1, ∀i

用Lagrangian乘子法进行求解，可以化为：

s.t.αi≥0, ∀i

对于数据点线性不可分的情况，添加惩罚因子，对线性可分的式子进行变换即为线性不可分的情况[12]，数学公式如下所示：

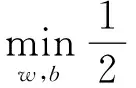
s.t.yi(wxi-b)≥1-ξ, ∀i

转换到Lagrangian乘子问题即为

s.t. 0≤αi≤C,∀i

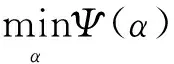
代入并对原函数求导等于零可解得

式中：

并根据盒子原理可以推导出

式中：

式中：

B是边界的集合[14-15]。

2.2 算 法

具体的算法流程如下所示。

Step1：应用启发式搜索算法，选择合适α1与α2；

Step2：计算α2的上、下界H与L；

Step3：更新α2；然后更新α1；

Step4：更新所有fi；更新b；

Step5：判断是否满足终止条件，若是则停止；若不是则返回Step1。

3 并行SMO算法

根据对串行算法与很多数值例子的分析，可以看出算法的运行时间绝大部分集中在Step4更新fi的操作中，为了更好地加速算法，可以对fi的更新转移到GPU上进行计算。

3.1 具体并行算法

Step1：算法初始化；

Step2：从CPU端传输数据到GPU端；

Step3：如果threadID=0，那么选择α1和α2；并对选择的两个参数进行更新操作；

Step4：对于所有 threads，更新参数fi；

Step5：如果threadID=0，更新参数b；

Step6：转到Step3，除非达到终止条件。

3.2 并行程序优化

(1) 考虑到Step4中更新fi的操作，其没有数据依赖关系，对其并行计算可以获得很好的加速效果，考虑到x1，x2，Δα1，Δα2，y1，y2等参数是每个计算进程所共用的，结合CUDA编程架构中的Shared Memory，可以一次性读入这些数据，然后Block内线程共用，这样可以获得更少的Global Memory与线程之间的数据交换，可以达到更好的计算效率[7]。

(2) Step3中参数的选取工作放到GPU端进行计算，是因为如果其在CPU端计算的话，需要GPU在更新完参数fi后，把相应更新后的参数传回到CPU端，考虑到异构平台数据交换的高额代价，平衡CPU单线程计算与GPU单线程计算，把参数α1和α2的选择工作放到GPU端完成是合理的。

(3) 考虑到利用启发式搜索来选择α1和α2两个参数，这个过程分为两个过程，第一步是选择任意一个违反KKT条件的点，不妨即为α1，然后在所有数据点中，搜索使得E1-E2模最大的点，记为α2，然后对两者进行更新操作。整个过程是求最大化的过程，其过程也可并行化，把数据分块，每个块先求得局部最大值，然后合并之后求得全局最大值。

并行算法的流程如图1所示。

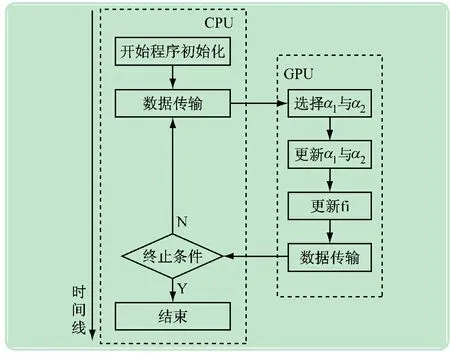
图1 并行算法程序流程图

4 数值实验

(1) 实验环境采用HP Z400工作站，显卡是另外配置的，为Nvidia Geforce GTX650。详细参数配置如下：

操作系统Windows 7， 64 b，内存大小4GB，编程环境Visual Studio 2012，CPU：Intel(R) Xeon(R) W3520@ 2.67GHz，4核，GPU：显卡型号：Nvidia GeForce GTX650，显存大小：1GB，GDDR5，显卡带宽：86.4 GB/s，核心频率：1 111 MHz，内存频率：1 350 MHz，SM 数目：12，SP 数目：384。

(2) 实验数据选择随机生成的数据来进行测试，我们选择在超平面wT·x≥51*Dim时数据点为正类，以wT·x≤49*Dim时数据点为负类，生成数据满足xi∈[0,100];∀i。

(3) 运行参数选择，Block的大小为256，线性排列。Grid的大小为N/Blocksize；选择N为Blocksize的整数倍，以数据点个数和数据点维数为变换参数，可以得到运行结果如表1所示。

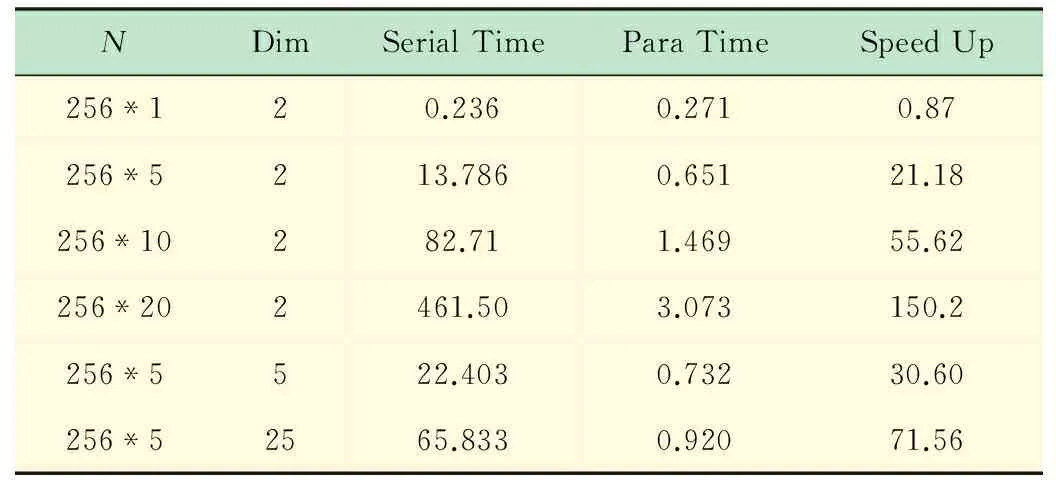
表1 数据运行结果

由表1的前4行可以看出，随着数据数目的增大，加速效果更加明显，这是由于随着记录数目的增大，GPU可以越来越达到满负载运行，由开始的分析我们知道，串行程序执行过程中，90%以上的时间用来执行fi的更新操作，在本例中，这步骤的更新操作在O(1)的时间即可完成，所以加速效果非常明显。当随着数据量的增大，GPU满负载之后，加速比逐渐达到一个上限，考虑到GPU内SP数目为394，其不会超过这个数值[7]。

由表2中第2、5、6行可以看出，随着数据维数的增大，加速比也是逐步增大的，这是由于串行程序执行过程中频繁读取数据，维数的增大对串行程序影响较大[15]；相比之下，GPU并行执行时间虽然也是有时间的增加，但是增加幅度较小，这是由于GPU访存过程充分利用了共享显存，它可以很显著地降低显存的读取时间，从而使得算法达到一个很好的加速效果。

5 结 语

在GPU计算平台下，利用CUDA编程接口，通过把SMO算法并行化，，可以达到一个很可观的加速效果。由于显卡是自己重新配置的计算专用显卡，此加速比会显示的高，但是不能否认GPU通用计算的高效性，尤其是面对这种SIMD计算模式时，更是显示出GPU计算的魅力。SMO算法在求解二次规划问题中是非常重要的算法，通过把其并行化算法实现也使得自己对问题认识的更加深刻。

[1] Cortes C, Vapnik V. Support-vector networks[J]. Machine learning, 1995, 20(3): 273-297.

[2] Platt J. Fast training of support vector machines using sequential minimal optimization[J]. Advances in Kernel Methods—support vector Learning, 1999, 3.

[3] 多核系列教材编写组.多核程序设计[M]. 北京：清华大学出版社, 2007,9.

[4] Cao L J, Keerthi S S, Ong C J,etal. Parallel sequential minimal optimization for the training of support vector machines[J]. IEEE Transactions on Neural Networks, 2006, 17(4): 1039-1049.

[5] 朱齐丹,张 智,邢卓异. 支持向量机改进序列最小优化学习算法[J]. 哈尔滨工程大学学报,2007(2): 183-188.

[6] http://en.wikipedia.org/wiki/CUDA.

[7] 张舒, 褚艳利. GPU高性能运算之CUDA[M]. 北京：中国水利水电出版社, 2009.

[8] http://en.wikipedia.org/wiki/Opencl.

[9] http://msdn.microsoft.com/en-us/library/bb524831(v=VS.85).aspx.

[10] C++ AMP: Language and Programming Model Version 1.0[M]. Microsoft Corporation. 2012,8.

[11] Vapnik V. Estimation of Dependences Based on Empirical Data[M]. Springer-Verlag, 1982.

[12] Vapnik V. The Nature of Statistical Learning Theory[M]. Springer-Verlag, 1995.

[13] Lee C, Jang M G. Fast training of structured SVM using fixed-threshold sequential minimal optimization[J]. ETRI Journal, 2009, 31(2): 121-128.

[14] Joachims T. Making large scale SVM learning practical[R]. Universität Dortmund, 1999.

[15] Zhang H R, Han Z Z. An improved sequential minimal optimization learning algorithm for regression support vector machine[J]. Journal of Software, 2003, 14(12): 2006-2013.

An Improved Parallel SMO Algorithm Based on CUDA

TANGBin-feia,LINChaob，HUANGDia

(a. College of Science; b. Network and Technology Educational Center，China University of Petroleum, Qingdao 266580, China)

The Sequential Minimal Optimization algorithm is presented to solve the time consuming problem in support vector machine training. This algorithm is accelerating the original algorithm by making the “chunking” minimal. For different datasets, this algorithm can reach 100x～1 000x speedup. But the performance of this algorithm is also bad with the dataset increasing. GPU computing is very popular nowadays. To accelerate this algorithm, this article proposes the parallel algorithm based on the SIMD model. The main point is to identify the two argumentsα1andα2. After solving local optimum, thereby updating all parameters is a naturally parallel process. And the form of SIMD parallelism is consistent with GPU computing model. By computationally intensive part of the transfer parameter update calculations to the GPU, the algorithm can be accelerated. Experiments show that the parallel algorithm can reach 150x speedup.

SMO; CUDA; parallel SMO algorithm

2015-12-01

汤斌飞(1990-)，男，江苏江阴人，研究生在读，研究方向是数值计算。

Tel.：18506488138，0532-86983413；E-mail：tangbinfei@163.com

林 超(1977-)，男，山东栖霞人，硕士，工程师，研究方向：计算机技术、算法分析与设计。

Tel.：18678933396；E-mail：linchao@upc.edu.cn

TP 391

A

1006-7167(2016)04-0140-04