过程控制测量信号数字滤波方法优化

李 芹， 王 伟， 彭道刚,b

(上海电力学院 a.自动化工程学院; b.上海发电过程智能管控工程技术研究中心，上海 200090)



过程控制测量信号数字滤波方法优化

李 芹a， 王 伟a， 彭道刚a,b

(上海电力学院 a.自动化工程学院; b.上海发电过程智能管控工程技术研究中心，上海 200090)

在对过程控制实验装置上某一液位测量信号分析的基础上，提出了兼顾平滑性和准确性的滤波性能指标。应用该指标分别编写了查询一阶惯性滤波法、中位值滤波法和平均值滤波法的最佳滤波参数程序。通过对3种方法最佳滤波参数的分析，确定了一阶惯性滤波法更适合过程控制实验装置的这一液位信号，该方法的实验室装置应用效果也证明了其有效性。

一阶惯性滤波； 中位值滤波； 平均值滤波； 滤波指标

0 引 言

我校的部分过程控制实验装置由于受实验室搬迁，设备台套数有限,使用率高，以及仪表本身寿命等因素影响，导致目前的实验装置的测量信号普遍存在大量噪声，学生开展特性试验几乎无法进行在线读取特征点数据，只能通过后期的数据拟合求取特征点，建立数学模型。如果进行控制实验，需要根据对象的数学模型计算调节器参数，由于测量信号的噪声的影响不仅使实验时间大大延长，同时也引入了一些拟合处理中数据点不足导致的新的误差，最终导致计算的调节器参数的控制效果很差。同时，由于测量噪声的存在，几乎无法进行微分控制[1-2]。

为了避免更换测量仪表产生的大量费用，同时解决学生无法正常开展实验的情况，笔者对测量信号进行了滤波应用研究。经典的快速滤波方法有一阶惯性滤波、中位值滤波及平均值滤波等方法，这些方法的应用研究[3-6]，及其相关实验软件应用[7-8]和实验平台应用[9-10]都比较成熟，但普遍存在选择滤波参数的随意性，而导致滤波效果不好；而一些智能方法如粒子群算法、免疫算法、自适应遗传算法对数字滤波器的优化研究也取得了很好的效果，但这些方法又普遍存在计算量大，难以应用到在线滤波中的特点[11-12]。本文通过对过程控制实验装置的测量信号分析，提出了兼顾平滑性和准确性的滤波指标，研究快速滤波方法应用中的最佳滤波参数选择问题，以便解决实验装置目前存在的问题。

1 测量信号分析

过程控制实验装置如图1所示，在该装置中，选择编号为6的水箱液位测量信号进行分析。若欲获取该测量信号，①需要通断多个手动阀，保证水从底部的编号1的不锈钢水槽，编号2的绿色电泵，编号3的蓝色电动调节阀，编号4的蓝白色流量变送器，编号5的水箱，编号6的水箱，然后重新流回到编号1的水槽。②安装在编号6的水箱底部的压力变送器输出4～20 mA电流信号连接到实验台下部的编号7的位置，通过跨接电阻转换为1～5 V电压信号，对应连接到编号8的8个AI通道的0通道，信号将通过编号9的A/D转换器转换为数字信号，通过编号10的串口通信端口与主机相连，通过上位机软件平台可以完成该测量信号的采集。

图1 过程控制实验装置

开启上位机软件平台，完成串口检测及相应通道设置，启动电动调节阀、电泵及相应的测量设备，进行测量信号的数据采集。图2所示为串口检测过程，图3中蓝色液位测量信号为采集到的水箱液位信号。可以看出，选定的这台设备的该液位测量信号存在较大的噪声信号，不但不利于建模，也无法进行控制。

图2 串口检测状态

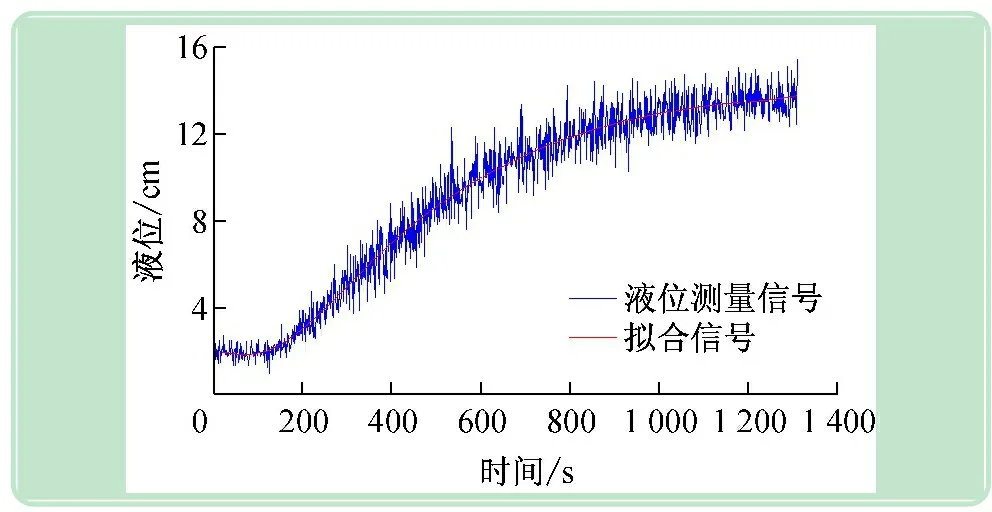
图3 水箱液位测量信号

2 滤波指标及参数寻优算法

对原始采样数据进行滤波，一般关注滤波结果是否准确及数据变化是否平稳，因此，定义两个指标：准确性偏差和平滑性偏差。

准确性是指滤波后的数据偏离原始数据的程度，准确性越好，滤波后的数据越能反映原始数据的有效信息。借助Matlab中的拟合函数polyfit对测量信号进行10次多项式拟合，其结果如图3中的红色拟合信号，具体的点用变量Yn(i)表示，i=0，1，…,n，以此拟合结果作为基准，液位测量信号用Y(i)表示，准确性偏差Ey定义如下：

(1)

平滑性是指滤波后的数据变化曲线是否平滑，平滑性偏差Ex定义如下：

(2)

把准确性偏差与平滑性偏差的代数和定义为滤波效果的总评价指标E，

E=Ex+Ey

(3)

根据“总偏差”指标，编写具体的滤波参数寻优程序，寻找总偏差最小时所对应的滤波参数，以保证在该滤波参数下所得到的滤波输出值即满足准确性指标，也满足平滑性指标。

3 快速滤波算法寻优

3.1 一阶惯性滤波参数寻优

一阶惯性滤波法又称为一阶低通滤波法，其算法为：

式中：k为滤波系数；X(i)为本次采样值；Y(i-1)为上次滤波输出值；Y(i)为本次滤波输出值；Ts为采样时间；Tf为滤波时间。

一阶惯性滤波就是对本次采样值和上次滤波输出值进行加权。所以当滤波时间越小时，滤波器也就越灵敏，滤波效果相对比较波动；反之，滤波效果相对比较平滑。但随着滤波时间的增大，滤波输出值会偏离原始数据，失去准确性。

根据滤波指标，编写查询最佳Tf的程序，程序流程图如图4所示。设定滤波时间常数的范围为[0,60]，运行寻优程序后，输出结果为Tf=11 s，在整个寻优过程中滤波指标变化如图5所示。当选择滤波时间为11 s，对原待滤波数据进行滤波处理的结果如图6所示。

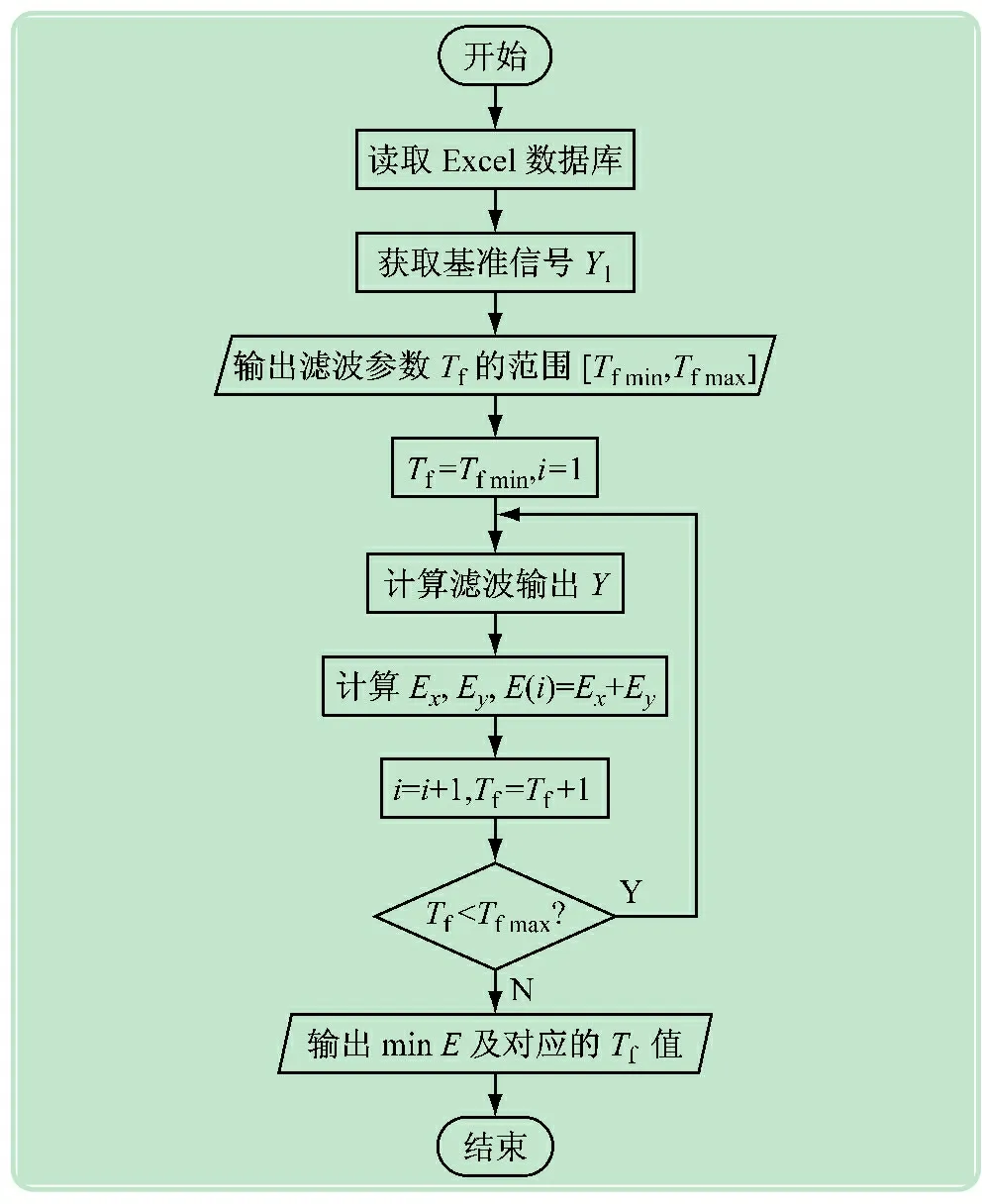
图4 一阶惯性滤波参数寻优算法流程图

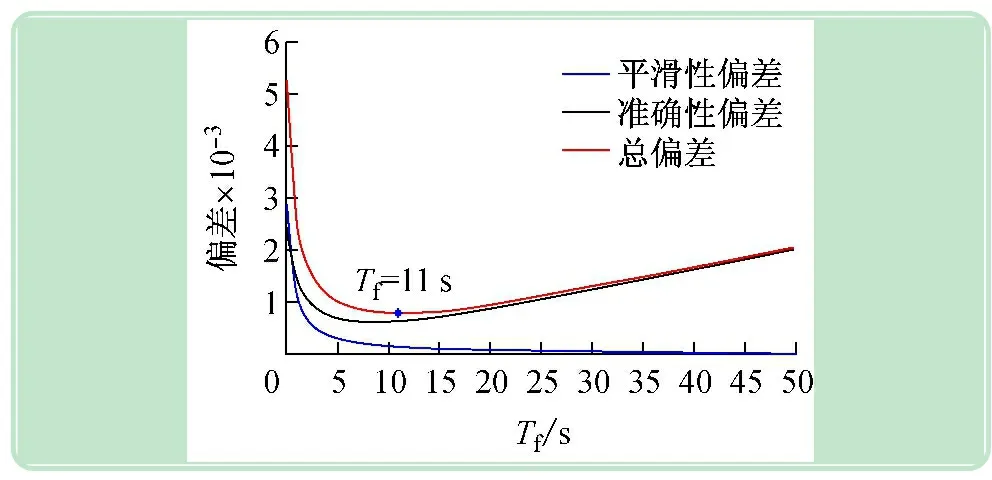
图5 滤波时间与滤波指标的变化关系

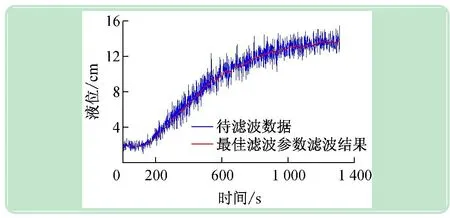
图6 Tf=11 s滤波效果曲线图

3.2 中位值滤波参数寻优

中位值滤波法较为简单，连续采样N次(N取奇数)，把N次采样值按大小排列，取中间值为本次有效值，即取中间值作为一次滤波输出值。主要实现方法为：先确定样本区间N的长度，N=2L+1，则第i次滤波输出值，即区间[i-L,i+L]内的中位值。编写类似图4算法的寻优程序来查找最佳滤波参数N，设定样本长度范围为[0,301]，运行寻优程序后，输出结果为N=199，在整个寻优过程中的滤波指标变化如图7所示。当选择N=199时，对原待滤波数据进行滤波处理结果如图8所示。由图7、8可以看出，中位值滤波法滤波效果明显优于一阶惯性滤波法,但其缺点也显然，即运算量大，且存在输出延迟，实时性不好，因此当N较大时，不适于在线滤波。另外，从图8中滤波后的曲线起始段和最后面都出现了偏离中心趋势的现象。由于起点和终点都存在左端或者右端不满足N=199样本长度的现象，而且越靠近，两段样本长度越短，效果会比较差。

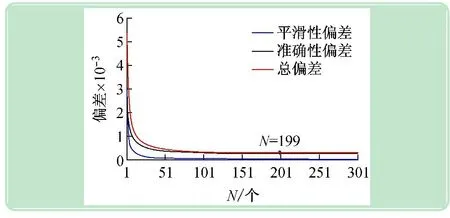
图7 样本长度N与滤波指标的变化关系图

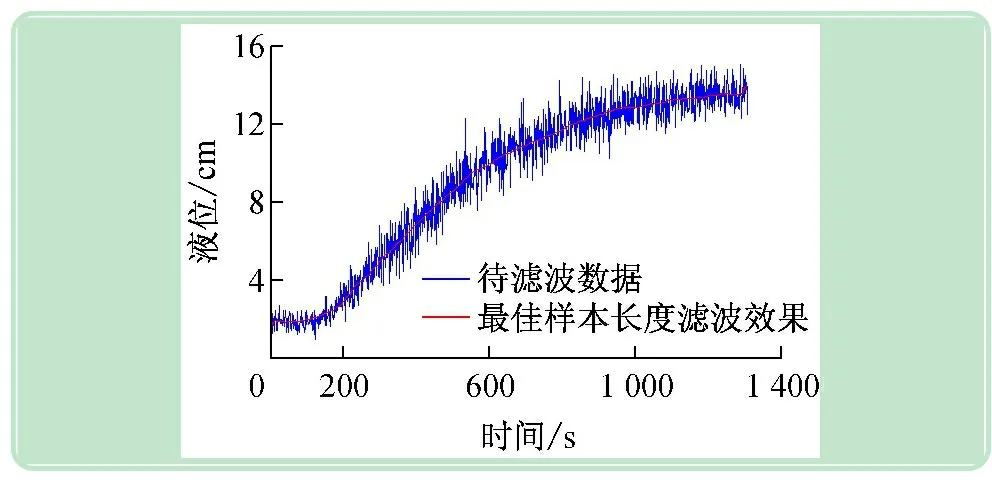
图8 样本长度N=199滤波效果曲线图

3.3 平均值滤波参数寻优

平均值滤波法和中位值滤波法比较相近，同样是先选取N个长度区间，然后求取该区间的算数平均值。实现方法为：先确定样本区间N的长度(N=2L+1)，则第i次滤波输出值，即区间[i-L,i+L]内所有采样点的算数平均值。编写类似图4算法的寻优程序来查找最佳滤波参数即样本长度N，设定样本长度的范围为[0,301]，运行寻优程序后，输出结果为N=143，在整个寻优过程中的滤波指标变化情况如图9所示。当选择N=143时，对原待滤波数据进行滤波处理的结果如图10所示。由图9、10可以看出，平均值滤波法对本文的携带随机干扰的测量信号滤波效果较好，缺点和中位值滤波法一样，即运算量大，实时性差，当N较大时，不适应在线滤波，尤其对于测量速度较慢或要求数据计算速度较快的实时控制不适用。另外，在滤波数据的起始位置和结束位置均存在样本长度较短，效果较差的问题。

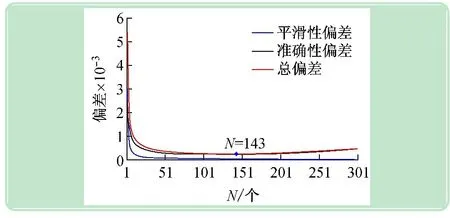
图9 样本长度N与滤波指标的变化关系

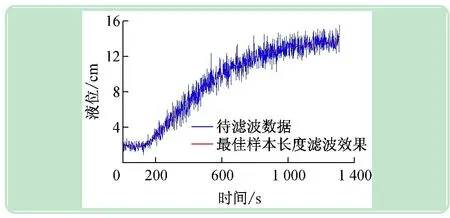
图10 样本长度N=143滤波效果曲线

4 具有最优滤波参数的快速滤波应用

针对以上3种方法的研究结果可以看出，中位值法和平均值法寻优的滤波参数结果比较大，不适于在线滤波。所以，将本文研究的一阶惯性滤波方法应用于我校的过程控制实验装置测量信号，滤波结果如图11所示，图12是相继进行的没有设置滤波参数的测量信号情况。对比两图，可以看出滤波效果和研究的结论一致，兼顾平滑性和准确性，滤波效果得到了很大的改善。

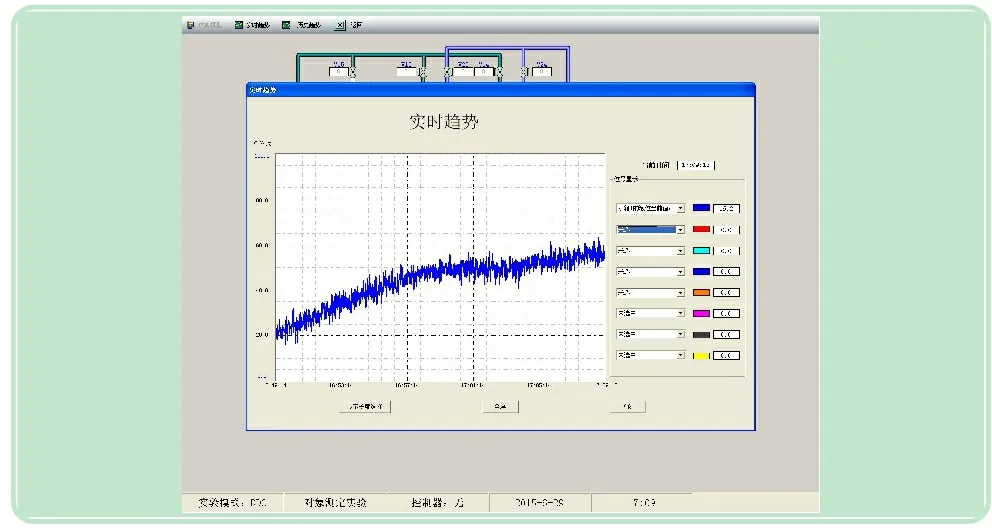
图11 具有最佳滤波参数的一阶惯性滤波后液位测量信号

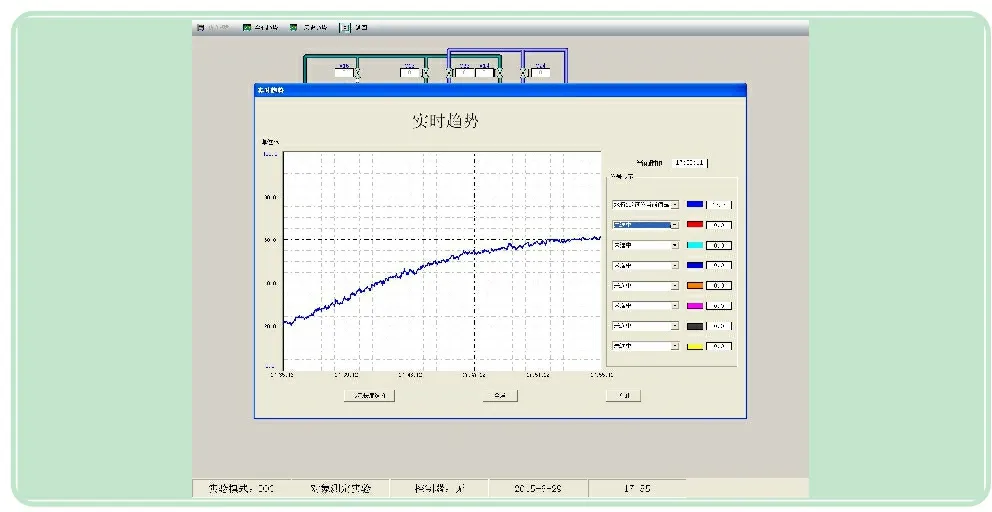
图12 未进行滤波的液位测量信号

5 结 语

本文提出了兼顾准确性和快速性的滤波指标，根据滤波指标进行了3种快速滤波方法参数寻优的方案，并根据具体寻优结果，把最适合本文测量信号的一阶惯性寻优方案结果应用于过程控制实验装置，效果很好。本文的快速滤波方法寻优方案也可以应用于任何过程参数，根据测量参数就可以查找到最优的滤波参数，即在中位值和平均值方法查找的滤波参数较小且满足滤波指标的情况下，优先选择这两种方法，若滤波参数过大，不适于在线滤波时，选择一阶惯性滤波方法。该方法虽然是针对实验室过程装置提出的方案，也能很好地应用于工业过程。

[1] 郭莹莹，马文渊，李丘林. 提高教学实验设备使用率的探索[J]. 实验室研究与探索，2015，34(4)：263-266.

[2] 周勇义. 试论实验室与设备管理工作对青年教师成长的支撑作用[J]. 实验室研究与探索，2015，34(3)：243-245.

[3] 甘 震. 基于MATLAB的数字滤波器设计[J]. 科技信息(学术研究)，2008(21)：499-500.

[4] 陈 君. 滤波技术研究[J]. 工业控制计算机，2014(12)：157-158.

[5] 唐 炜，张 莉，周世恩,等. 联合数字滤波在涡轮检测数据采集系统中的应用[J]. 江苏科技大学学报(自然科学版)，2011，25(3)：235-238，257.

[6] 傅彩芬，房 方. 球杆系统的数字滤波与控制[J]. 实验室研究与探索，2013，32(9)：13-15，27.

[7] 占荣辉. 仿真软件在数字滤波教学中的应用[J]. 信息系统工程，2011(3)：104-107.

[8] 于兰兰，张厚升. 数字滤波技术的MATLAB辅助教学[J]. 中国校外教育，2012(8)：88.

[9] 王丽萍，冯建文，施占一. 基于数字滤波算法的风冷热泵机组实验台测控系统设计[J]. 计算机应用，2012，32(S1)：208-210，213.

[10] 高兴泉，王立国. 数字滤波仿真实验台开发[J]. 实验室研究与探索，2014，33(1)：29-32，163.

[11] 宋定宇. 基于粒子群算法的数字滤波器优化与仿真[J]. 计算机仿真，2013，30(8)：356-359，375.

[12] 倪 龙. 基于免疫算法的IIR数字滤波器优化与实现[J]. 信息技术，2011(5)：115-118.

Optimization of the Filtering Methods for Process Control Measuring Signals

LIQina,WANGWeia,PENGDao-ganga,b

(a. College of Automation Engineering; b. Shanghai Engineering Research Center of Intelligent Management and Control for Power Process, Shanghai University of Electric Power, Shanghai 200090, China)

Based on the analysis of water level signals of process control experiment platform, the filtering criterion coordinating smooth and accuracy is proposed. With this filtering criterion, the best filtering parameter searching program is designed for first-order inertial filtering method, median filtering method and average filtering method. By analyzing the three best filtering parameters of the three methods, the first-order inertial filtering method is selected for the real-time filtering of water level signals in process control experiment lab. The result of lab application of this method shows the method is valid.

first-order inertial filtering; median filtering; average filtering; filtering criterion

2015-07-02

上海市“科技创新行动计划”高新技术领域项目资助(15111106800);上海市科学技术委员会工程技术研究中心项目资助(14DZ2251100);上海高校市级精品课程(沪教委高[2014]33号)

李 芹(1975-)，女，河北泊头人，讲师，主要从事热工过程建模及优化控制教学科研工作。

Tel.:021-35303137；E-mail:liqin@shiep.edu.cn

TP 274

A

1006-7167(2016)04-0026-04